Jaap's Puzzle Page

7x7x7 V-Cube

7x7x7 V-Cube

This puzzle is a cube which is built from smaller cubes, 7 to an edge, i.e. a 7×7×7 cube. Like a Rubik's Cube each slice can rotate, which rearranges the small cubes on the surface of the puzzle. The six sides of the cube are coloured, so every corner piece shows three colours, every edge piece shows 2 colours, and every face centre only one.

The V-Cubes worldwide patent was granted to inventor Panagiotis Verdes on 2 December 2004, WO 2004 103497.

The number of positions:

There are 8 corner pieces with 3 orientations each, 12 middle edge pieces with 2 orientations each, 24 inner edge pieces and 24 outer edge pieces apparently with 2 orientations each. There are 6 types of centre pieces, 24 pieces of each type. This gives a maximum of 8!·12!·24!8·38·260 positions. This limit is not reached because:

This leaves 8!·12!·24!8·37·210 / 4!36 = 19,500,551,183, 731,307,835,329,126, 754,019,748,794,904, 992,692,043,434,567, 152,132,912,323,232, 706,135,469,180,065, 278,712,755,853,360, 682,328,551,719,137, 311,299,993,600,000, 000,000,000,000,000, 000,000,000,000,000 = 1.95·10160 positions.

Links to other useful pages:

V-Cubes homepage has an on-line shop, and a solution method like this one.

Like the normal cube, there are several types of solution. Here I will only give the 'Edge-Matching' solution method.

Notation:

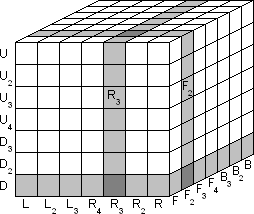Let the faces be denoted by the letters L, R, F, B, U and D (Left, Right Front, Back, Up and Down). Clockwise quarter turns of a face layer are denoted by the appropriate letter, anti-clockwise quarter turns by the letter with an apostrophe (i.e. L', R', F', B', U' or D'). Half turns are denoted by the letter followed by a 2 (i.e. L2, R2, F2, B2, U2 or D2). The above is the same notation as for the 3×3×3 cube. An internal slice will be denoted by adding a subscript 2, 3 or 4. So F2 is a clockwise turn of the slice immediately behind the Front face, and F3' is an anti-clockwise turn of the slice immediately behind that. Note that these denote a slice only, so such a move will not disturb the corners of the cube.
The location of any piece can be denoted by listing the three faces/slices it lies in.


Solution

Phase 1: Solve centres
The method below solves the U centres without disturbing any already solved faces. Simply repeat this for each of the faces.

  1. Find any centre piece edge that belongs on the U face. Hold the cube so that it lies on the F or D face.
  2. If the piece is in the front face, turn F to put the piece at the top right, i.e. in the U2 or U3 layer, and the R2, R3, or R4 slice. If it is in the bottom face, turn D to put the piece at the front right, i.e. in the F2 or F3 slice, and the R2, R3, or R4 slice.
  3. Turn the U face so that there is an incorrect piece at the back right location where the piece belongs.
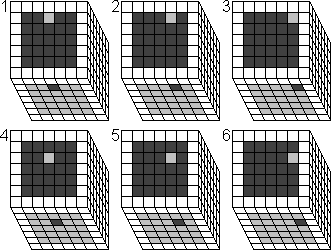  4. Do one of the following move sequences to insert the centre piece:
    1. From F U2 R4 to U B2 R4: Do R4 U' L2' U R4' U' L2
    2. From F U2 R3 to U B2 R3: Do R3 U' L2' U R3' U' L2
    3. From F U2 R2 to U B2 R2: Do R2 U' L2' U R2' U' L2
    4. From F U3 R4 to U B3 R4: Do R4 U' L3' U R4' U' L3
    5. From F U3 R3 to U B3 R3: Do R3 U' L3' U R3' U' L3
    6. From F U3 R2 to U B3 R2: Do R2 U' L3' U R2' U' L3
    7. From D F2 R4 to U B2 R4: Do R42 U' L22 U R42 U' L22
    8. From D F2 R3 to U B2 R3: Do R32 U' L22 U R32 U' L22
    9. From D F2 R2 to U B2 R2: Do R22 U' L22 U R22 U' L22
    10. From D F3 R4 to U B3 R4: Do R42 U' L32 U R42 U' L32
    11. From D F3 R3 to U B3 R3: Do R32 U' L32 U R32 U' L32
    12. From D F3 R2 to U B3 R2: Do R22 U' L32 U R22 U' L32
  5. Repeat a-d until all 24 centre pieces in the U face are correct.
  6. Repeat a-e for each of the faces.

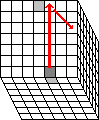Phase 2: Match up the inner edges.
In this phase the inner edge pieces are matched up to form matching pairs.

  1. Find any inner edge piece that is not yet matched up with its middle edge piece. Hold the cube so that this piece lies at the U F R3 location.
  2. Find the matching middle edge piece. Use any face moves to bring it to the U B location.
  3. Check that the middle edge piece shows a different colour on the U face than the inner edge piece. If not, then flip over the middle edge piece by doing B' U R' U'.
  4. Find any unmatched inner edge piece and put it at the U R B3 location, without disturbing the other two pieces. If there is no other unmatched inner edge, then do U2 R3 U2 R3 U2 R3 U2 R3 U2 R3 to make some new unmatched inner edge pairs and try again.
  5. Do R3 B'RB R3'.
  6. Repeat a-d until all inner edges are matched up with the middle edges.

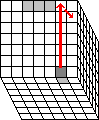Phase 3: Match up the outer edges.
In this phase the outer edge pieces are matched up to the middle/inner edge triplets.

  1. Find any outer edge that is not yet matched up with its middle triplet. Hold the cube so that this piece lies at the U F R2 location.
  2. Find the matching edge triplet. Use any face moves to bring them to the U B location.
  3. Check that the triplet shows a different colour on the U face than the outer edge piece. If not, then flip over the triplet by doing B' U R' U'.
  4. Find any other unmatched outer edge piece and put it at the U R B2 location without disturbing the other pieces. If there is no other unmatched pair, then do U2 R2 U2 R2 U2 R2 U2 R2 U2 R2 to make some new unmatched outer edges and try again.
  5. Do R2 B'RB R2'
  6. Repeat a-e until all edges lie in matching edge quintuplets.

Phase 4: Solve the cube.

  1. Solve the cube by turning outer faces only, using any method for the 3×3×3 cube. This is always possible.