Jaap's Puzzle Page

Floppy Cube

Floppy Cube Floppy Cube twisted

This puzzle was invented by Katsuhiko Okamoto, and made by Gentosha Toys in Japan. It is like a 1×3×3 Rubik's Cube, so it consists of 9 cubes arranged in a square, and each side of 3 cubes can be given a half turn. Halfway through a move the centre cubie deforms slightly to allow the corner cubies to remain connected, and that is where its name comes from.

The number of positions:

There are 4 edge pieces which do not move but can be flipped, and 4 corner pieces that do move but cannot be flipped (their orientation is determined by their location). This would give a total of 24·4! = 384 positions. This is not reached however due to a parity constraint. The parity of the corner permutation is the same as the parity of the number of flipped edges. There are therefore 24·4!/2 = 192 positions.

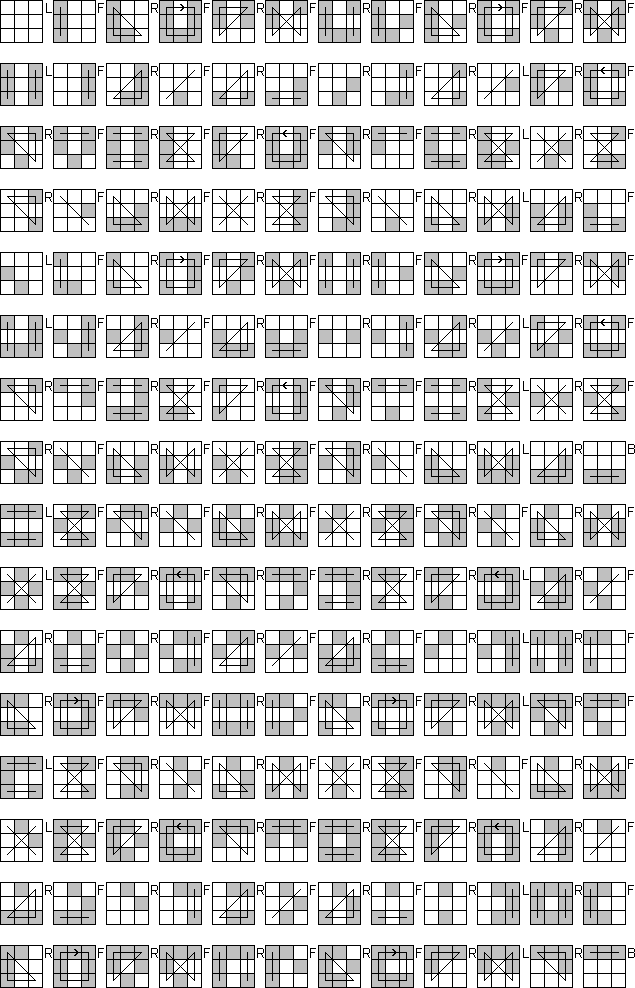
I performed a computer search for this puzzle. The following table shows how many positions there are for each number of moves from the solved position. It shows that it can be solved in at most 8 moves (4.4271 on average).

Moves    # Positions
01
14
210
324
453
564
631
74
81
Total   192

The single antipodal position that takes 8 moves to solve is the 'superflip' R FB R F RL F.

Links to other useful pages:

Gentosha Toys is the manufacturer of this puzzle.
Meffert's puzzles Uwe Mèffert's site sells this puzzle as well as many others.

Notation:

The letters B, F, L and R will denote a move twisting the Back, Front, Left, and Right side of the puzzle.

Solution:

  1. Find the corner piece that belongs at the back left location. It will have the same side colours as the back and left edge pieces.
  2. Do any moves you need to put it in its back-left location.
  3. If the back edge needs to be flipped over, do the move sequence LBL.
  4. If the left edge needs to be flipped over, do the move sequence BLB.
  5. Find the corner piece that belongs at the back right location.
  6. If it is not yet at the the back-right location, then do R or FR to put it in place.
  7. If the right edge needs to be flipped over, do the move sequence RFRFR.
  8. If the front edge needs to be flipped over, do the move F. The front corners should automatically be correct as well.

Below is a graph that can be used to solve the puzzle in the minimum number of moves. By reorienting the puzzle, possibly turning it upside down, any mixed position will match one of the positions shown in the graph.

Floppy Cube graph

Devil's Algorithm:

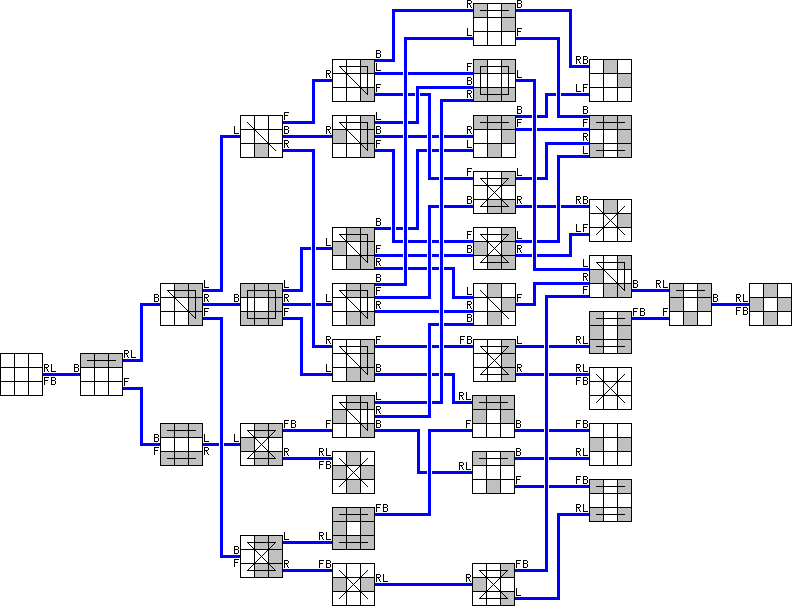
Let P be the move sequence: L FRFRFRFRFRF L FRFRFRFR L RFRFRFRFRFR L RFRFRFRFRFR L R.
The move sequence PFPB PFPB is 192 moves long, and visits all possible positions exactly once, returning it to how it was at the beginning. This kind of sequence is sometimes called a Devil's Algorithm, and is a Hamiltonian cycle on the Cayley Graph. If you apply it to any mixed position, it will solve it somewhere along the way. A blindfolded person could always solve the floppy cube by doing this sequence as long as there is someone there to say 'stop' when it is solved.

Hamilton cycle for the Floppy Cube