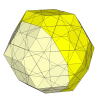
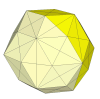
Ideas for further puzzles
Introduction
Below I will try to classify the various puzzles which are closely related to the
Rubik's Cube. By doing this, I not only list which puzzles have been made, but more
importantly which puzzles have not. Some of these might be developed, or at least
give a few ideas for producing new rotational puzzles. I will make several assumptions:
- All axes of rotation used in the puzzle have the same order. This
disqualifies the Domino for example because
its sides have order 2 while the top and bottom faces have order 4.
- The puzzles have a fully symmetrical three dimensional shape, meaning that
it has the same kind of symmetry as one of the platonic solids. This
also means that most of the puzzles that change their shape (such as the
Octagon/Barrel) are not considered here.
- The cuts through the puzzle are flat planes. It is possible to use cone
shaped cuts, or in fact cuts of any other shape with complete rotational
symmetry. With such cuts the cut lines across the surface of the puzzle
can be much more freely chosen. In the more complicated puzzles on this
page the cuts could be used to reduce the number of pieces.
There are three obvious symmetry groups for these puzzles; tetrahedral,
cubical/octahedral, and icosa/dodecahedral symmetry. In each case the axes
can go through all the corners, all the faces, or all the edges of the associated
Platonic solid. I will assume only one such set of axes is used. It might be
possible to combine for example corner and face turns in a single puzzle, but
I won't consider such puzzles here, only those with all axis types the same.
Neither will I discuss other symmetry groups such as dihedral ones, again
because not all axes are the same.
Note that in the text below I will consider an axis to end at the centre,
so that a Rubik's cube has 6 axes (one for each face) rather than only 3.
Overview
| Tetrahedron | Cube | Octahedron | Rhombic Dodecahedron | Dodecahedron | Icosahedron | Rhombic Triacontahedron |
|---|
4 Axes
Tetrahedron corners
Tetrahedron faces |
|
|
|
|
|
|
|
6 Axes
Tetrahedron edges
Cube faces
Octahedron corners |
|
|
|
|
|
|
|
8 Axes
Cube corners
Octahedron faces |
|
|
|
|
|
|
|
12 Axes
Cube edges
Octahedron edges
Rhombic Dodecahedron faces |
|
|
|
|
| |
|
|
12 Axes
Dodecahedron faces
Icosahedron corners |
|
|
|
|
|
|
|
20 Axes
Dodecahedron corners
Icosahedron faces |
|
|
|
|
|
|
|
30 Axes
Dodecahedron edges
Icosahedron edges
Rhombic Triacontahedron faces |
|
|
|
|
|
|
|
Puzzles with 4 axes of rotation, i.e. the faces or corners of a tetrahedron.
These can mostly be made by using the Skewb / Pyraminx
mechanism, the 4-armed spider.
- Tetrahedron
Two variations already exist.
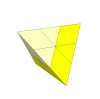
The standard tetrahedral puzzle is
the Pyraminx, a tetrahedron with three pieces to an edge. The
corners are fixed on axes. The tips are trivial as they do not interact with other pieces.
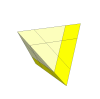
The Halpern-Meier Tetrahedron is outwardly like the Pyraminx except that it has no trivial tips and the main
cuts are deeper (w.r.t. the corners) giving face centres which move
around the puzzle. The mechanism has the faces fixed on the axes so that the corners are actually the
moving pieces, but a mechanism with the corners on axes and the faces moving is also possible and
completely equivalent.
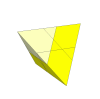
If the main cuts are instead slightly shallower than the pyraminx then centre pieces also appear
but these do not move, and therefore might as well be fixed to the central mechanism too. This
puzzle has never been produced as far as I know.
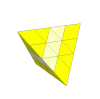
It is theoretically possible to make a tetrahedron with more
pieces to an edge. A size 4 Pyraminx, also known as the Master Pyraminx, can be made
by using the Diamond Skewb as a basis. The four free face
centres of the Diamond become the pyraminx face centres, the four fixed corners
have built on them a seperately twistable octahedral vertex piece and tip. Between
the Diamond's tips and the added vertex pieces 12 new edge pieces have to be added.
The only potential difficulty with this model is that the 12 edge pieces
would seem to fall off when a size 3 vertex is turned. This is not a
problem however since the edges only do this on one side, so they can
have a deeper-reaching lopsided tongue inside a groove.
This puzzle would have 6!·24·34·12!/2 = 2.2·1014 positions,
ignoring the tips.
A tetrahedron of size 5 however would not be possible with this type of
mechanism because the central edge pieces would have to be able to overhang
on either side. That mechanism can be used if the layers are of differing widths,
or if the puzzle is pillowed (i.e. the sides bulge out a bit).
- Cube
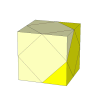
The only cube-shaped puzzle
which is based around a 4-armed spider is the Skewb. This puzzle has
essentially 8 axes of rotation since the cuts go exactly through the centre of the cube. The fact
that on the outside there is no difference between the set of corners on axes and those that are not,
gives rise to the two possible mechanisms of the Halpern-Meier Pyramid above.
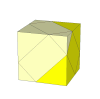
The same mechanism could also produce a Skewb with off centre cuts which does have only tetrahedral
symmetry.
- Octahedron
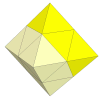
The octahedron is the dual of the cube so the same ideas apply in this case. The Skewb
Diamond, the only mass produced puzzle in this category, has essentially 8 axes just
as with the Skewb above.
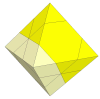
An off centre version is again possible, and
Tony
Fisher has made them (Fisher's Octaminx). It is in fact a pyraminx with its corners drastically
cut down. Note that the cuts are offset so much here that one set of face centres has disappeared.
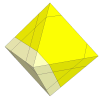
By using shallower cuts, four new face centre pieces appear, but as with the tetrahedron they do not
move at all so might as well be fixed to the puzzle centre.
- Rhombic Dodecahedron
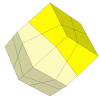
A Rhombic Dodecahedron skewb makes for a very pleasing puzzle. Halfway
through a turn (i.e. 60 degrees) the surfaces line up and form trapezoids.
This puzzle is more confusing than an ordinary Skewb where the faces are
marked, because the strange angles make it easy to lose your way. With
six colours, each piece also has a mirror image on the other side, and
the face pieces are easily confused. Again,
Tony
Fisher has made these.
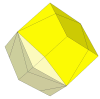
With the above puzzle the cuts are through the centre. Shallower cuts are also possible,
for example by using the Pyraminx mechanism.
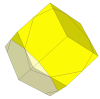
By using shallower cuts, four new face centre pieces appear, but as with the tetrahedron and octahedron they do not
move at all so might as well be fixed to the puzzle centre.
- Dodecahedron
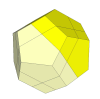
This puzzle has been produced under the name Ultimate Skewb by Uwe Mèffert.
It has also at one time been called the Pyraminx Ball. Its mechanism is exactly that of the
Skewb, and can be solved in the same way except that the orientation of all the pieces matter.
This puzzle is more confusing than an ordinary Skewb where the faces are
marked, because the strange angles make it easy to lose your way. With
six colours, each piece also has a mirror image on the other side, and
the face pieces are easily confused.

With the above puzzle the cuts are through the centre. Shallower cuts are also possible,
for example by using the Pyraminx mechanism instead to give a puzzle which has 4 large
turning corners and 6 free moving pieces made from two triangles.
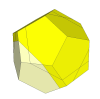
By using shallower cuts, four new face centre pieces appear, but as with the tetrahedron and octahedron they do not
move at all so might as well be fixed to the puzzle centre.
- Icosahedron
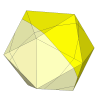
Since this is the dual of the dodecahedron, a Skewb mechanism can be embedded
in exactly the same way.
Tony
Fisher has made these.
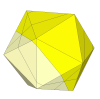
With the above puzzle the cuts are through the centre. Shallower cuts are also possible,
for example by using the Pyraminx mechanism.
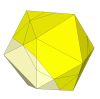
By using shallower cuts, four new face centre pieces appear, but they do not
move at all so might as well be fixed to the puzzle centre.
- Rhombic Triacontahedron
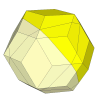
As this shape has the same symmetries as the dodecahedron, a Skewb mechanism can be embedded
in exactly the same way.
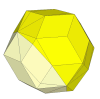
With the above puzzle the cuts are through the centre. Shallower cuts are also possible, for example by using the Pyraminx mechanism.
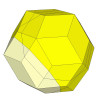
By using shallower cuts, four new face centre pieces appear, but they do not
move at all so might as well be fixed to the puzzle centre.
Puzzles with 6 axes of rotation, i.e. the faces of a cube, corners of an
octahedron or even edges of a tetrahedron.
The standard mechanism for these is the 6-armed spider as used in the Rubik's Cube, though
other mechanisms are often needed with puzzles which have deep cuts, i.e. cuts through the
centre of the puzzle dividing it into halves.
- Tetrahedron
A tetrahedron does not have cube symmetry, so if we embed a cube
mechanism inside it will change shape unless only half turns are
allowed.
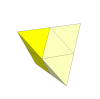
One variation already exists, the Pyramorphix. It is a tetrahedron with
two pieces to an edge, and as such is based on a 2×2×2 Rubik's cube
mechanism. The only difference between them is that this time the orientations
of four of the pieces do not matter.
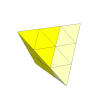
A version with three pieces to an edge would be an interesting one. It would be like a
Rubik's cube with four corners completely missing, but where orientation of the face centres matter.
It again changes shape unless only half turns are allowed.
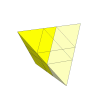
By using deeper cuts, the the Rubik's Cube corners do not disappear. This puzzle is usually called
the Mastermorphix, and many hobbyists have built it. By pillowing the faces outwards, the layers can
by made the same thickness, and such a Mastermorphix is produced commercially by Uwe Mèffert.
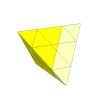
By using shallower cuts instead, a set of fixed face centres appear. The large amount of overhang
during a turn will make it very hard to make this puzzle.
- Cube
This leads to the standard cubes of various sizes.
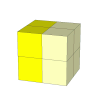
The 2×2×2 cube.
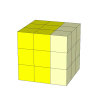
The 3×3×3 cube.

The 5×5×5 cube.
With the 7×7×7 and larger cubes overhanging pieces become a problem.
To make such cubes it is necessary to use layers of different thicknesses, a pillowed
shape instead of a cube, or some non-standard mechanism.
- Octahedron
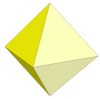
One version based on a 2×2×2 cube would have one piece to an edge and cuts through
the middle of the puzzle. A version called Okki was made in the 80s in Germany. You could make
one of these yourself by combining two Pyramorphixes, but Mèffert makes these under the
name Pyradiamond.
A larger version with 2 pieces to an edge would make a nicer puzzle. It
would be an octahedral version of Dogic (which is
icosahedral). The face centres behave like a 2x2x2 cube, an it can be made by extending such
a cube. A spherical version of this is the Marusenko Sphere.
You can actually make an equivalent puzzle by painting a 4×4×4 cube such that
each 2×2×2 block has one colour, except for the face centres which should be left
blank.
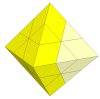
Versions with three pieces to a side do exist, however none of them have
a cut through the exact centre of the puzzle. Instead they are based on
the standard 3×3×3 cube mechanism, and only allow tips of size 1 or 2 to
turn. Ignoring the tips, these are just like the Rubik's cube without
corners but where the orientations of the face centres matters. See the
octahedron page.
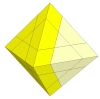
Trajber's Octahedron is similar to the octahedron above, in the same way that
the Halpern-Meier pyramid relates to the Pyraminx; it has no trivial
tips, and the main cuts are slightly deeper. It therefore has face centres
which correspond to the corners of the underlying cube mechanism.
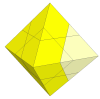
A shallower set of cuts leads to fixed face centres appearing.
- Rhombic Dodecahedron
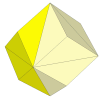
It is well worth embedding a 2×2×2 mechanism inside the rhombic
dodecahedron. Each piece has only one face in common with any adjacent
piece. If only six colours are used (opposite faces the same colour)
this leads to a very tricky puzzle. Given one edge of a piece, there
are three pieces that seem to fit. Only one will lead to the correct
solution.
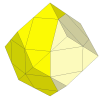
If a 3×3×3 mechanism is embedded inside a rhombic dodecahedron another
fairly nice puzzle results. It is like the cube except that orientations
of edges do not matter, but that of the centre pieces does.
A 4×4×4 mechanism cannot be used with all the layers of the same width,
because the edges and corners would drop off, but a different mechanism
could be used, for example a 2×2×2 mechanism that is extended on each face.
This is similar to the size 2 octahedron above but without its face centres.
- Dodecahedron
The dodecahedron does not have cube symmetry, so if we embed a cube
mechanism it will change shape unless only half turns are allowed.
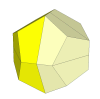
This 2×2×2 version is a great little puzzle, especially with 6 colours, for exactly the
same reasons as the 2×2×2 rhombic dodecahedron above.
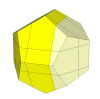
If a 3×3×3 mechanism is embedded inside a dodecahedron a nice
supercube results, as the orientation of all the pieces, including the centres is visible.
- Icosahedron
The icosahedron does not have cube symmetry, so if we embed a cube
mechanism it will change shape unless only half turns are allowed.
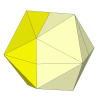
A 2×2×2 mechanism in the icosahedron gives a nice looking puzzle but
it is not as hard to solve as the dodecahedral one.
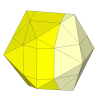
Here a 3×3×3 mechanism is embedded inside a icosahedron. In the picture shown here,
the cube's corner pieces correspond to trianglular face pieces that have no visible orientation.
By using slightly deeper cuts those pieces will include part of the adjacent faces and so
their orientation does become visible. Either way, the cube's face centre orientation is
visible.
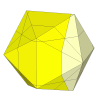
By using shallower cuts the underlying cube's corner pieces disappear. The puzzle becomes like
an edges-only cube, but with visible face centre orientation. The same thing occured with the octahedron.
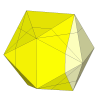
By using even shallower cuts new unmovable pieces appear.
- Rhombic Triacontahedron
The rhombic triacontahedron does not have cube symmetry, so if we embed a cube
mechanism it will change shape unless only half turns are allowed.
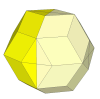
A 2×2×2 mechanism in the rhombic triacontahedron gives a nice looking puzzle but
it is not as hard to solve as the dodecahedral one.
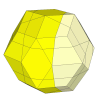
Here a 3×3×3 mechanism is embedded inside a rhombic triacontahedron.
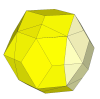
By using shallower cuts the underlying cube's corner pieces disappear. The puzzle becomes like
an edges-only cube, but with visible face centre orientation. The same thing occured with the octahedron.
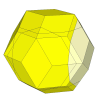
By using even shallower cuts new unmovable pieces appear.
- Other shapes

A Stella Octangula can be made by combining two Pyramorphixes (actually both
the octahedron above and stella could be made from two). This gives a puzzle
based on a 2×2×2 cube but made of two intersecting tetrahedra.
This puzzle was produced in Germany in the 80s. It has been called the
Star of David, but is now made by Mèffert with the name Pyrastar.
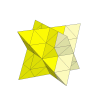
A stella octangula with 4 pieces along each diagonal edge could
theoretically have a 3×3×3 cube embedded in it, with the middle layers twice
as thick as the outer ones. This has the interesting property that the edge
pieces of the underlying cube correspond to two seemingly separate parts of
the surface. It may be hard to adapt the standard cube mechanism to this shape since the
corners overhang during a turn, so the middle layer probably has to be less thick for it
to work.
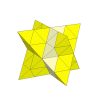
A stella octangula with 4 pieces along each diagonal edge could also
move like a proper 4×4×4 cube. The mechanism would be very difficult,
again due to overhanging corners during turning. It would behave like
a Rubik's Revenge with the face centres marked and edge pieces which
come in indistinguishable triplets. There will not be a parity problem
when solving this puzzle.
Puzzles with 8 axes of rotation, i.e. the corners of a cube or faces of an
octahedron.
The standard mechanism for this would be the 8-armed spider, but in deep-cut puzzles like
the Skewb a 4-armed spider is used.
- Cube

There are two versions available commercially. The best known one is the Skewb, which has
cuts exactly through the centre of the cube.
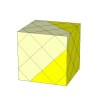
By using slightly shallower cuts, edges and centre pieces appear.
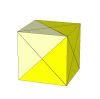
By making the cuts even shallower, you get the Dino Cube.
Its cuts go diagonally through three adjacent faces.
This gives a cube with only 12 edge pieces and no others visible on the
surface. It gets its name from the fact that the original version had pictures of
dinosaurs on the sides. Its mechanism is based on an 8-armed spider, i.e. a stella
octangula with the edges held between each adjacent pair of rotating tips with a
tongue/groove system. This is much like a simple version of
Alexander's Star, except that the pieces cannot be flipped.
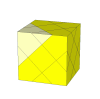
If the cuts of a dino cube are made shallower still, then fixed face centres appear, as
well as rotating corner pieces.
Consider a cube which on the outside looks like a combination of the skewb and dino
cube, i.e. each face is cut along its diagonals, and has diagonal cuts connecting
the edge midpoints. It seems nearly impossible to me to find a simple
mechanism that allows both Skewb and dino moves. However the same outward
shape could also be produced by a dino cube where each tip has two layers.
A mechanism for this is possible even though the edges will overhang (see
above) but it may need to be quite accurately made
to stop it being too loose. It has been made by Katsuhiko Okamoto and is
called the Lattice Cube.
- Octahedron

One octahedral puzzle where the faces turn is the Skewb Diamond. It has a
Skewb mechanism, and has cuts through the centre of the puzzle, and there are two
pieces along each edge.
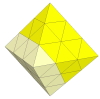
Several people have designed the mechanism for a face-turning octahedron with three pieces to an
edge, and it has recently become commercially available. It is based around an 8-armed spider,
where the tips (invisible from the outside) hold the 12 edges together like a dino-cube and
these in turn hold the other pieces.
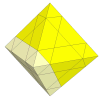
If the 8 cuts are shallower, i.e. the face layers are less thick, then the puzzle will have 8
triangular face centres, which are simply the tips of the 8 axes in the mechanism.
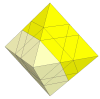
Making the cuts a bit deeper also creates new triangular face centre pieces, but now turning a face also moves the adjacent
face centres.
- Rhombic Dodecahedron

The deep cut rhombic dodecahedron has already been discussed above.
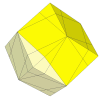
Here the cuts go exactly through three vertices of the rhombic dodecahedron. It can have
the same mechanism as the face-turning octahedron.
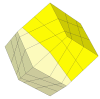
Making the cuts a bit deeper creates new vertex pieces, and turning a vertex also moves the adjacent
vertex pieces.
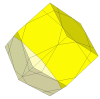
If the 8 cuts are shallower then the puzzle will also have 8 new vertex pieces,
which are simply the tips of the 8 axes in the mechanism.
- Dodecahedron

The deep cut dodecahedron, the Skewb Ultimate has already been discussed above.

Here the cuts go exactly along three edges and three face diagonals of the dodecahedron. It can have
the same mechanism as the face-turning octahedron. This puzzle looks deceptively simple because the
cuts coincide with so many edges.
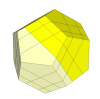
Making the cuts a bit deeper creates new vertex pieces, and turning a vertex also moves the adjacent
vertex pieces.
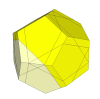
If the 8 cuts are shallower, then the puzzle will have also 8 new vertex pieces,
which are simply the tips of the 8 axes in the mechanism.
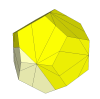
If the 8 cuts are even shallower then many pieces disappear, resulting in a puzzle
similar to the Rainbow Cube.
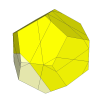
If the 8 cuts are shallower still, then some unmovable edge pieces appear.
- Icosahedron

The deep cut icosahedron has already been discussed above.
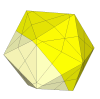
Here each cut goes exactly through three face centres of the icosahedron. It can have
the same mechanism as the face-turning octahedron.
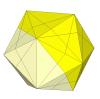
Making the cuts a bit deeper creates small triangular face centres, and turning a face also moves the adjacent
face centres.
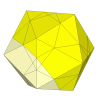
If the 8 cuts are shallower, then the puzzle will have also 8 new face centres,
which are simply the tips of the 8 axes in the mechanism.
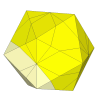
If the 8 cuts are even shallower then many pieces disappear, resulting in a puzzle
similar to the Rainbow Cube.
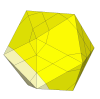
If the 8 cuts are shallower still, then some unmovable edge pieces appear.
- Rhombic Triacontahedron

The deep cut rhombic triacontahedron has already been discussed above.
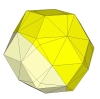
Here each cut goes exactly through three short face diagonals of the rhombic triacontahedron. It can have
the same mechanism as the face-turning octahedron.
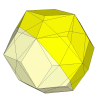
Making the cuts a bit deeper creates small vertex pieces, and turning a vertex also moves the adjacent
vertex pieces.
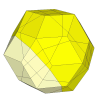
If the 8 cuts are shallower, then the puzzle will have also 8 new vertex pieces,
which are simply the tips of the 8 axes in the mechanism.
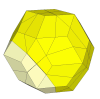
If the 8 cuts are even shallower then many pieces disappear, resulting in a puzzle
similar to the Rainbow Cube.
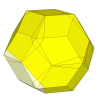
If the 8 cuts are shallower still, then some unmovable face centres appear.
- Other shapes
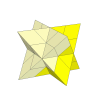
The Skewb mechanism could be embedded in the Stella Octangula to make a really nice
looking puzzle, but this does not add much interest to solving it.
Embedding the Dino-cube mechanism gives a trivial puzzle.
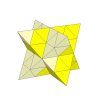
The shape does however suggest a much more interesting puzzle. Starting
with a Master Pyraminx (see above), it is possible
to add on size 2 tetrahedra on each of the faces to build a stella octangula. It seems
possible (but somewhat tricky) to adjust the mechanism outlined before
to allow this puzzle to work. This puzzle would have
12!/2·12!/2·38 = 3.8·1020 positions,
ignoring the tips.
Puzzles with 12 axes of rotation, around the edges of the cube or octahedron.
Very few such puzzles have been made commercially. These puzzles generally allow jumbling,
where a partially completed move may still allow an adjacent face to turn, and so cause the
shape to change and different types of pieces to take each others place.
The reason that jumbling is possible is best seen on the face-turning rhombic dodecahedron.
The faces of the rhombic dodecahedron can be turned so that two opposite sides of the rhomb end up
where the other two sides belong. Since all the angles between the faces are the same, the cuts
on those two sides will line up.
- Cube
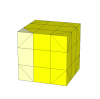
In this shallow cut puzzle a move involves giving the triangular prism along any
edge a half turn. Its mechanism could be based on a 12-armed spider.
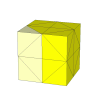
Here slightly deeper cuts are used so that the face centres and edges disappear.
This puzzle used to be called the Half Chop by Bram Cohen, but is now better known as the Helicopter Cube. This is the first puzzle of this type to
have become commercially available.
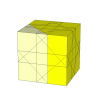
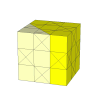
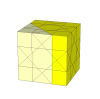
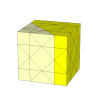
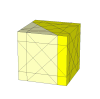
As the cuts get deeper, many more pieces appear. It is unlikely that these is a nice mechanism for these.

This puzzle is deep cut, so a move involves twisting exactly half the cube along a diagonal plane.
Bram Cohen has coined the name Little Chop for this puzzle, but it is also known as the 24 Cube.
- Octahedron
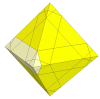
In this shallow cut puzzle a move involves giving the section along any
edge a half turn. Unlike the cube, the octahedron immediately cuts into
many pieces this way.
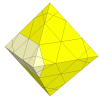
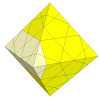
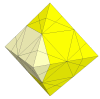
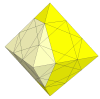
As the cuts get deeper, many more pieces appear and disappear. It is unlikely that these is a nice mechanism for these.
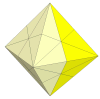
This is a deep cut octahedron, where a move involves twisting half the octahedron
through 180 degrees, and is similar to the 24 Cube above.
- Rhombic Dodecahedron
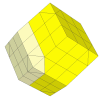
This is a face-turning rhombic dodecahedron, where each face only does half turns.
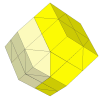
Here slightly deeper cuts are used so that the face centres and edges disappear.
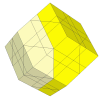
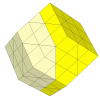
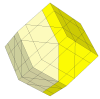
As the cuts get deeper, many more pieces appear. It is unlikely that these is a nice mechanism for these.
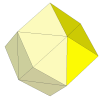
This puzzle is deep cut, so a move involves twisting exactly half the puzzle,
and is similar to the 24 Cube above.
Puzzles with 12 axes of rotation, i.e. faces of dodecahedron or corners of
an icosahedron.
- Dodecahedron

The standard version is the Megaminx.
In this the cuts are shallow which results in a puzzle where each face has a fixed face
centre and 5 edge and 5 corner pieces.
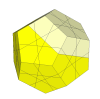
With slightly deeper cuts, a new type of edge piece appears.
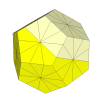
If the cut of a face goes through the centres of the adjacent faces, you get the
Pyraminx Crystal, produced by Mèffert. The megaminx's face centres and edge pieces
have disappeared. Each face has 5 edge pieces and 5 corner pieces, but if it is turned, the 5 adjacent
edges turn with it.
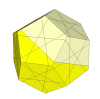
Deeper cuts will result in puzzles for which the mechanism is likely to
be very different. It has face centres which move around the puzzle.
In puzzles with octahedral symmetry (e.g. Skewb) this is less of a
problem because those could be built around their tetrahedral symmetry
(hence the Skewb has a 4-armed spider instead of an 8-armed one).
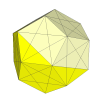
Here the cuts go through the vertices, so there are no corner pieces any more.
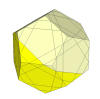
With still deeper cuts corner pieces reappear.
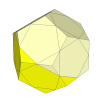
This is the dodecahedral analogue of the Skewb, with cuts exactly through the
centre of the puzzle. It is commonly called the Pentultimate, but has not been
commercially manufactured.
Having more than one cut per face will produce rather a lot of pieces.
Versions of the megaminx have been made with 2 or 3 layers per face, called the
Gigaminx and Teraminx. Even a Petaminx has been made with 4 layers per face.
- Icosahedron
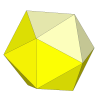
The most common puzzle of this type is the Impossiball.
Although it is actually shaped like a sphere, it is basically an icosahedron where
every cap of 5 faces rotates about the corner.
The Dogic puzzle has one cut like the Impossiball, and the second cut through
the midpoints of the edges.
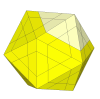
With a slightly shallower cut, face centres and edge pieces appear. It is the
icosahedral equivalent of Trajber's Octahedron.
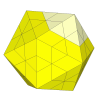
It would be straightforward to make a puzzle with a shallower cut, which
goes through the centre of the triangular faces. A second cut could be
added to create tips, and it then looks just like an icosahedral version
of the pyraminx. It would not be much more difficult to solve than the
pyraminx however, as no new techniques would be needed.
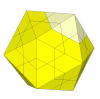
With an even shallower cut, unmovable face centres appear.
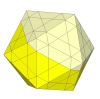
With deeper cuts than the Impossiball, many more pieces appear - 12 vertex pieces, 30 edge pieces, and 60 more face centre pieces.
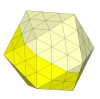
Slightly deeper cuts and the central face pieces disappear.
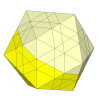
Deeper still and new face pieces appear.
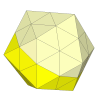
When the cuts go directly through the centre, we get an icosahedral analogue of the Skewb Diamond.
- Rhombic Triacontahedron
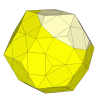
The rhombic triacontahedral version of the Megaminx.
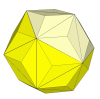
The rhombic triacontahedral version of the Impossiball.
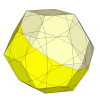
With deeper cuts than the Impossiball, many more pieces appear - 12 vertex pieces, 30 face centre pieces, and 60 edge pieces.
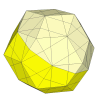
Slightly deeper cuts and the 20 Impossiball pieces disappear.
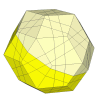
Deeper still and 20 new vertex pieces appear.
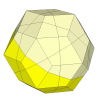
The deep cut rhombic triacontahedron.
Puzzles with 20 axes of rotation, i.e. corners of a dodecahedron or
faces of an icosahedron.
As far as I know, no such puzzles have been made commercially, though a few have been custom built.
This type of puzzle generally allows jumbling (provided the cuts are deep enough). Consider a face
of the icosahedron. It has three directly adjacent faces, and six other faces that it touches at a corner.
Those six faces come in two distinct types, mirror images of each other. You can turn a face so that
the pieces that belong with three of the six faces line of with the three faces of the other type.
- Dodecahedron
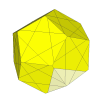
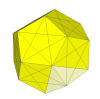
Here the cuts go through the three adjacent corners, or shallower than that.
This puzzle is a bit like the Dino-cube. The main difference is that it has
fixed face centres, and there is also a vertex piece between the edges.
It would not be very difficult to solve, similar to the pyraminx, though
flipping edges is a bit more involved.
Having two cuts (first as above, second through edge midpoints) will
produce a nice puzzle, but I suspect it needs a very accurately produced mechanism.
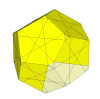
Deeper cuts produce new corner pieces and adjacent face pieces. The corner pieces will overhang on all sides so
there is no easy mechanism for this unless the shape is changed, e.g. pillowed.
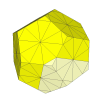
Here the original face centre pieces all disappear. This would be a nice puzzle, even if the corner pieces are not included (because they still overhang).
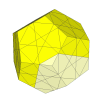
Now new face centre pieces appear. If the cuts are deep enough that the corners no longer overhang, the puzzle allows jumbling to occur.
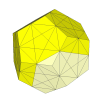
Edge pieces disappear.
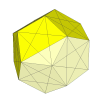
Here each cut goes through six vertices and along three edges, making for a simple looking puzzle.
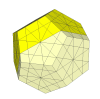
Here the cuts go through three face centres.
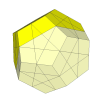
A deep cut puzzle - 10 cutting planes bisecting the dodecahedron.
- Icosahedron
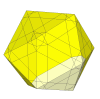
A face-turning icosahedron. Here the cuts are shallow enough that there are triangular centre pieces. Note that there are
many small pieces even with the shallow cuts.

The cuts now go through the exact face centre points so the face centre pieces have disappeared.
New face centres appear.
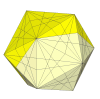
As the cuts get deeper many beautiful patterns occur, though it is unlikely that any of these could be made into a practical puzzle.
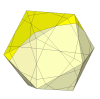
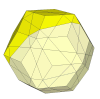
The deep cut icosahedron with 10 cutting planes bisecting it.
- Rhombic Triacontahedron
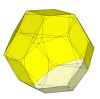
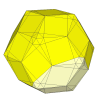
Shallow cuts give pieces of wildly different sizes.
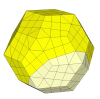
This is a very nice looking puzzle.
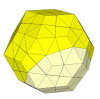
Another nice looking one, with relatively few pieces.
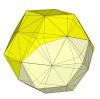
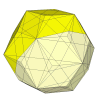
Deeper cuts produce oddly proportioned piece sizes again.
Here deep cuts are used, bisecting the puzzle.