


Mind Jewel is a puzzle invented by Alexander Polonsky. It consists of 12 pentagonal pyramids connected to each other by an elastic rope. The aim is to arrange the pyramids to make a single closed shape. This means that the pieces are arranged as if on the surface of a dodecahedron. The elastic enters and exits each piece through a slot on the sides, and you often choose which edge of the pentagon the elastic should enter or exit.
The pieces are as shown in the following picture:
The pieces are Blue, Red or Green, three of each. The colour order on mine is BRG BRG GRB BRG, but I am not sure if that is the same on all Mind Jewel puzzles. Number them 1 to 12, starting with the blue end. All intermediate pieces 2-11 allow the elastic to make a shallow left and a shallow right turn. Pieces 2, 6, 7, and 10 also allow a sharp left turn, and 6, 9, and 10 also allow a sharp right turn.
There are 12 pieces. Of the 10 pieces in the middle, at 5 pieces the elastic has only two angles it can make, at 3 pieces there are three possible angles, and at 2 pieces all four possible angles can be made. This gives a total of 25·33·42 = 13,824 possibilities. In practice there are far fewer since choices are often blocked by previous pieces of the arrangement. Nevertheless it is trickier than this low number suggests.
If you consider a solved Mind Jewel, the centres of the 12 pieces form the vertices of an icosahedron. The edges of this icosahedron are lines over which the elastic can go. Looked at in this way, solving the Mind Jewel is finding a Hamilton path on the icosahedron, i.e. a path that visits all vertices exactly once. The slots on the pieces restrict the kind of turn that the elastic can make at the the 10 intermediate vertices.
By computer I generated all possible Hamilton paths on the icosahedron graph. There are 1264 distinct ones given the first two vertices of the path. These break down as follows:
| 1264 paths | 752 paths with nonadjacent end vertices | 68 reflexive paths (they are their own inverse) |
| 342 non-reflexive paths, and their inverses | ||
| 512 paths with adjacent end vertices | 12 non-reflexive, non-repeating cycles each producing 12 paths and their inverses | |
| 10 reflexive, non-repeating cycles each producing 12 paths | ||
| 7 non-reflexive, repeating cycles each producing 6 paths and their inverses | ||
| 2 reflexive, repeating cycles each producing 6 paths | ||
| 1 non-reflexive, doubly repeating cycle, producing 4 paths and their inverses |
In the above table I call a path reflexive if it looks the same if you traverse it in the opposite direction. If the start and end vertices of the Hamilton path are adjacent, then you can connect them and have a Hamilton cycle. Removing any of the edges of such a cycle produces a Hamilton path. The most interesting of these cycles is the one with three-fold symmetry, which has four steps which are repeated twice more. It can be used to make a very nice snake pattern on the megaminx.
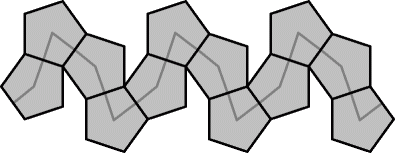
It turns out that of all these 1264 possible paths, only one can be achieved with the turning restrictions of the Mind Jewel. The solution is shown in the picture below.
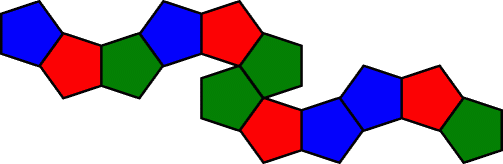
Starting from the end with a blue piece, the turns made by the elastic are:
two shallow left turns,
two shallow right turns,
a sharp right turn,
a sharp left turn,
two shallow left turns,
two shallow right turns.
Note that all the sharp turns are in the centre, and it is probably this that makes it so tricky to solve.