Analysis:

Virtually all of the analysis below is based on the paper by Mark Manasse, Danny Sleator, and Victor K. Wei which can be downloaded from Nick Baxter's Panex page.

Recursion

Like the towers of Hanoi, this puzzle can be solved recursively. One basic task is swapping a tower of n disks on a side peg with a single disk at level n on the middle peg. The picture below shows this. Let's call this task S_n, a swap of level n.

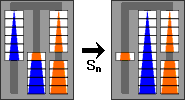
A simpler related task is to move a tower of n disks from a side peg to the middle peg. This similar to the swap S_n above, except that one piece is missing. If we can do S_n, then we can certainly do this by just leaving out any moves that would involve the missing piece. Let's call this task T_n, a transfer of level n.

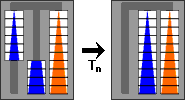
We can now set up the recursion, defining these level n tasks using smaller tasks of level n-1. The sequence of pictures below shows how this is done.

S_n = T_n-1 + S'_n-1 + X + S_n-1

T_n = T_n-1 + S'_n-1 + T_n-1

Here the inverse of a move or move sequence is denoted by a tick mark. Also new is the move sequence denoted by X, which consists of 4 moves and swaps the top two disks on the middle peg. Note how T_n is just like S_n but without the unnecessary X swap.

The cases T₁ and S₁ are trivial (1 and 3 moves respectively), so this shows that we can definitely perform all these swaps and transfers for any number of disks. To actually solve the puzzle we need to swap the two towers on the outside pegs. We can swap the two bottom disks as follows:

X_n = _LT_n + _LT'_n-1 + _RS_n + _RT'_n-1 + _LT_n-1 + _LT'_n

The L and R subscripts indicate on which side the move sequence is performed.
We can repeat this exchange for each level of the puzzle: X₁₀ + X₉ + X₈ + ... + X₁ exchanges the pieces at each level, thus exchanging the towers and solving the puzzle. This at least proves the puzzle can be solved.

Improvement

The method above is not at all optimal. First of all, the recursive definition of T_n has many cancellations in it:

T_n = T_n-1 + S'_n-1 + T_n-1
= T_n-1 + ( T_n-2 + S'_n-2 + X + S_n-2 )' + ( T_n-2 + S'_n-2 + T_n-2 )
= T_n-1 + S'_n-2 + X + S_n-2 + T'_n-2 + T_n-2 + S'_n-2 + T_n-2
= T_n-1 + S'_n-2 + X + T_n-2

Let's now see how many moves this would take, assuming that there are no cancellations or simplifications anywhere. Let t_n, s_n, and x_n be the number of moves of T_n, S_n and X_n respectively. From the relations above we get the recurrence relations:

s_n = 4 + t_n-1 + 2s_n-1
t_n = 4 + t_n-1 + t_n-2 + s_n-2
x_n = 3t_n-1 + 2t_n + s_n

If we use the boundary conditions s₁=3, t₁=1, we get the following table:

For ten disks this gives 64861 moves. Fortunately this is not optimal, so the real number is less. In particular, T₂ and S₂ need not be done in 5 and 11 moves respectively, but can easily be done in 3 and 8 moves, because we can make more efficient use of the space in the top row of the puzzle. Similarly, T₃ can be done in 9 moves. This results in the following table:

It turns out that there are some small move cancellations here or there in S and T, but even optimally T₁₀ needs 4875 moves so this is a rather good method for it. On the other hand, there is a much better way of exchanging the towers than doing the pairs at each level from the bottom up, because we can do much of the work on the top pieces during the exchange of the bottom pair. This is easiest to explain using the following sequence of moves, which we will call Z_n:

Z_n = _LS_n-1 + _RS'_n-1 + _RT'_n-1 + _LT_n-1

This transfers the top piece of the left stack across to the bottom of the right stack.

The two towers can now be exchanged as follows:

Solution₁₀ = _LT₁₀ + _LT'₉ + _RS₁₀ + Z₁ + Z₂ + Z₅ + ... + Z₈ + Z₉ + _LT'₁₀

The last Z₉ and _LT'₁₀ can provide some more cancellation:
Z₉ + _LT'₁₀ = ( _LS₈ + _RS'₈ + _RT'₈ + _LT₈) + (_LT₉ + _LS'₈ + X + _LT₈)'
= _LS₈ + _RS'₈ + _RT'₈ + _LT₈ + _LT'₈ + X + _LS₈ + _LT'₉
= _LS₈ + _RS'₈ + _RT'₈ + X + _LS₈ + _LT'₉

The idea behind this solution is that as soon as you have the largest blue piece in its correct place, you first fix the remaining blue ones above it. It is easier to do that first, separating the colours, because the orange tower can be built afterwards in its correct place without disturbing the blue pieces.

Given also that Z₁ is one move, and Z₂ seven, this leads to the following table:

This improves on the previous method by more than 30%. The best known solution uses this method, shortened slightly by some more simplifications and cancellations. It still uses 31537 moves, and that solution method has been proved optimal by computer search.

Solving any position

Given that the solution is so long, it is quite likely that at some point you will lose track of where you were in the solution. It is possible to deduce what to do by examining where the largest pieces are, and then the next largest pieces, and so on. Of course, this assumes the pieces are distinguishable (i.e. the Panex Silver, not Gold). To do this, you must of course understand what route these pieces take during the solution. Let's first look at the largest blue piece.

1. The large blue piece starts at the bottom of the left column.
2. All the pieces above it on the left peg are removed (and piled up on the middle and/or right pegs).
3. The large blue piece is moved to the middle peg, and slowly works its way down through the pieces of the middle peg, all the way until it is at the bottom.
4. Now the largest other piece on the middle or right peg is freed up, and worked down the middle peg, until it is the only piece on the middle peg other than the large blue piece.
5. The large blue piece swaps with that other piece, rising upwards a bit.
6. Steps d and e are repeated with the second largest piece that can be found on the middle or right peg, then the next largest, and so on. The blue piece therefore bubbles upwards on the middle peg while all the other pieces from the right peg build up a tower underneath it.
7. The blue piece then can be moved onto the empty right peg, to its solved position.