
Arithmetician Calculator No. 6
Video
History
Models
Advertisements and articles
Patents
Links
The Bair-Fulton Calculators are a clever combination of the addiator/troncet slide adder (e.g. the Pocket Adding Machine) and the dial adder (e.g. the Dial-A-Matic). The Arithmetician model has 6 dials. Each dial is a gear with teeth, but those teeth are only accessible at the top and bottom of the gear dial due to the cover over the dials. That cover has small windows showing the digits.
The label on the bottom of the wooden base has simple instructions:
| BAIR-FULTON
CALCULATOR |
|---|
|
Directions for Addition and
Subtraction on all BAIR-FULTON
Calculators. ADD ABOVE. SUBTRACT BELOW.
Insert pencil between teeth of the counter wheel at the desired number and always draw away from the red director tooth (the tooth dividing the bright from the black). If the pencil is in black teeth draw right to the red stop signal. If in bright, draw left to the red stop. The leftward stroke is always a carrying stroke—if blocked from carrying or entering to the red stop (by the red director tooth) continue leftward to the next wheel until pencil reaches the stop. TO CLEAR the machine, draw thumb from left to right along lower teeth of wheels. NOTE: For Multiplication and Division with the Mathmetician, see special instructions. BAIR-FULTON CO., YORK, PA. |
There is also a full instruction sheet.
The sheet is reproduced below:
BAIR-FULTON CALCULATING MACHINES
The all-important thing to remember about the operation of ANY adding machine is the LISTING: ACCURACY in inserting your pencil point (between the teeth of the counter wheel) at the desired number, in the correct decimal position on the machine, and in moving to the stop, is all that is required. The totaling is automatic; that is why it is called an adding machine. The machine makes no mistakes. If the result is incorrect, the mistake was made by you in the listing. At the left, is a diagram of the mechanical unit; a series of which, mounted upon a wood base, constitutes the mmacine. Two sets of number series appear on each dial; one above the horseshoe for addition, and the other below for substraction. TO CLEAR or to RESET the machine, draw your thumb from left to right along the thumb-groove and in contact with the lower teeth of the counter-wheels, so that an O appears in each total window. TO OPERATE the machine (for addition), insert pencil point at the desired number of the upper number series, and if you are in black teeth (and to the right of the red director tooth) move pencil rightward to the red stop. When you are in bright teeth (and to the left of the red director tooth) move pencil leftward to the red stop. When making a rightward movememt, the operation is completed in that decimal position. When making a leftward movement, the operation is not completed in that decimal position, but carried into and completed in the adjacent decimal position. Example: List 5 in the units dial (move right to the stop)—now add 5 —(move leftward, and carry, into the tens dial, and to the stop). Your result is 10 in the total windows. In subtraction, the operation of the machine is the same as in addition, except that you use the lower number series. After you have added a column of figures you can PROVE YOUR RESULTS (belore clearing your machine) by subtracting, successively, the same items; after which an O will appear in each total window, thus proving the accuracy of your work. 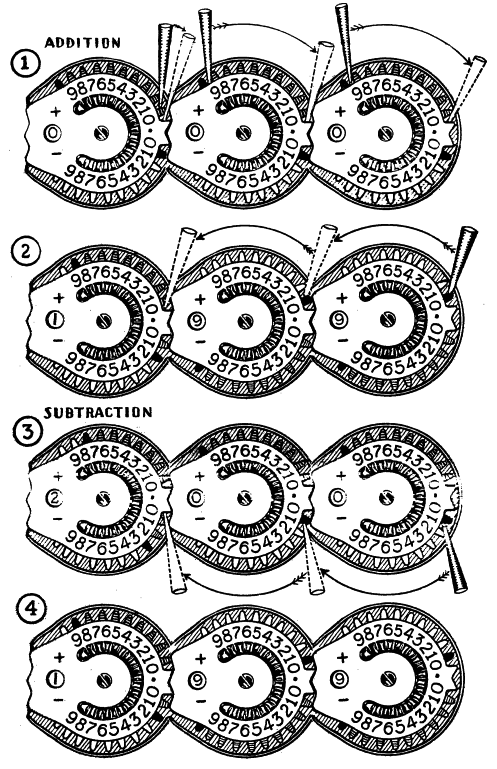
To make clear Ihe simple operation of the machine we have illustrated a very simple problem, in addition and subtraction, which involves the entire philosophy of the machine. ADDITION: 199 + 1 = 200. Graph No. 1 shows your pencil in the three decimal positions ready to list 199. The arrow shows the direction in which your pencil moves. The phantom view of the pencil shows the destination of the pencil (always to the red stop) after listing each numeral. Graph No. 2 shows the result (199) in the total windows after you have listed as in graph No. 1. Now to 199 you add 1. Graph No. 2 shows where you insert the pencil in the units dial, and its movement leftward to the tens dial where you are blocked, by the director tooth, from carrying or depositing the 1, therefore you confinue leftward to the hundreds dial, where the carrying is completed, and the result in your total windows is 200, as shown in graph No. 3. SUBTRACTION: 200 - 1 = 199 (without clearing your machine). From 200 listed in your machine, sutract 1. Graph No. 3 shows your pencil inserted at 1 in the units dial of the lower number series. Move pencil leftward to the tens dial; since you are blocked from carrying (or borrowing) move on leftward to the hundreds dial where you are permitted to enter to the stop and to carry (or borrow the 1). Your result is 199 in the total windows as shown in graph No. 4. Although the Bair-Fulton principle is broadly new and different from all other calculating machines, once you learn it and understand it, any problem in addition or subtraction can be done easily, quickly and accurately. | ||||||||||||||||||||||
This sheet explains addition and subtraction. A second sheet existed that explained multiplication and division, but that was probably only included with the No 8 model.
The machine's construction is cleverly simple. Each wheel is sandwiched between its individual back plate that has the grooves for the stylus, and its front plate that has the register window. These are held by a screw in the centre, and a small nail or pin on the right which not only fixes the orientation of the front plate, it also acts as a stop for the number wheel. The number wheel has a simple alignment mechanism consisting of a thin section that is bent up and acts as leaf spring cam which follows a series of dents on the underside of the cover plate.
The Bair-Fulton calculator was invented by Joseph Hershey Bair. He was born in Wellsville, Pennsylvania, in 1875. After a short stint as a school principal in 1895/6 he went to university, gaining an M.A. from Michigan University and a PhD from Columbia University in New York. He stayed on there as assistant to Nicholas Murray Butler, the head of the Department of Psychology and Anthropology. He made expeditions to the arctic to study the Inuit and to Mexico and Venezuela to study the local people there. From 1903 to 1912 he was at the State University of Colorado, heading the Department of Psychology and Philosophy.
In 1912 he turned his hobby of tinkering into his career. He had
made money from selling his design for a laundry drying machine,
so he used that to move to Haddonfield, New Jersey, set up a workshop
at his home (sometimes referred to as Bair Laboratories) and started
developing inventions full time. These included several related to cars,
engines and transmissions. See the patents section
below for more details.
In about 1920 he moved to Eberly's Mill, a small village near Camp Hill,
Pennsylvania, continued inventing from his home workshop, living there till
his death in 1947. Aside from inventing, he also wrote poetry, and wrote a fiction
novel titled "Black Sand".
Bair invented the Bair-Fulton calculator in 1927/1928, though the patent was only granted in 1933. I do not know who Fulton is, but presumably they were involved in manufacturing or marketing it. The machine seems to have been sold from 1935 till at least 1941, but it was never really successful. It was too expensive compared to both slide adders and dial adders.
There are 4 models, each with a name and a model number that is equal to the number of dials.
| Name | Model | Remarks |
|---|---|---|
| Arithmetician Calculator | No. 6 | The most common version. |
| ? | No. 7 | I have found only one picture of this online at Rechner Lexicon, but it is missing its label so I do not know its name. |
| Mathematician Calculator | No. 8 | This has movable paper strips for writing factors in a multiplication |
| Compilator Calculator | No. 11 | The dials are split into 3 rows (3+3+5) with stylus grooves connecting their ends |
The principle used in the Bair-Fulton calculator had been invented in 1905 in France by Louis Jean Guillaume Cabrol, resulting in the Arithmographe Clabor. Its implementation was inferior however, because the track from one wheel was not connected to the next, so it is not possible to carry over multiple digits in one movement. It is unlikely that Bair was aware of this machine. In the late 1940s the Addsubtractor, a machine very similar to the Clabor, was made in Australia for handling Sterling currency.
I have only found only a few ads for the Bair-Fulton Calculator.
These articles are all related to the inventor Joseph H. Bair.
Joseph H. Bair has many patents to his name. They include ticket machines (US 1,083,267, US 1,288,470), a centrifugal separator (US 1,246,035) a washing machine (US 1,350,353), a gradometer, (US 1,898,162). and various automotive patents such as a variable gear (US 1,285,585), fluid power transmission (US 1,354,592, US 1,423,386) and rotary engines (US 1,331,177, US 1,331,478, US 1,377,383, US 1,571,465).
Below are all Bair's patents related to calculating machines. Also included are a few patents by Louis Cabrol of the Arithmographe Clabor, a predecessor of the Bair-Fulton calculator that uses essentially the same principle, though its implementation is not as good. It is unlikely that Bair was aware of this machine.
| Patent | Filing date | Priority date | Name | Description |
|---|---|---|---|---|
| FR 352,510 | 18-03-1905 | 12-08-1905 | Louis Jean Guillaume Cabrol | Calculator rule |
| FR 7,860 E | 18-06-1907 | 14-11-1907 | Louis Jean Guillaume Cabrol | Calculator rule |
| US 1,210,753 | 15-11-1913 | 02-01-1917 | Joseph H. Bair; Speed Adding Machine Company | Adding machine See also: CA 175,299 |
| US 1,371,138 | 21-09-1915 | 08-03-1921 | Joseph H. Bair; Lewis H. Taylor, James O. David, William C. Haddock | Adding listing machine |
| US 1,940,069 | 07-01-1928 | 19-12-1933 | Joseph H. Bair | Bair-Fulton Calculator |
© Copyright 2023 Jaap Scherphuis, mechcalc a t jaapsch d o t net.