Douglas A. Engel is the inventor of the Engel's Enigma, a flat puzzle consisting of
two intersecting disks. His company, General Symmetrics Inc. marketed this puzzle in the early
1980s, as well as various colour variations, such as Puzzler Novice, Puzzler Challenger, and
Puzzler Avenger. Later he licensed Binary Arts to make a version which was called
Turnstile.
He is still developing variations of these "circle puzzles". Nowadays his puzzles
are lasercut from plastic sheets. You can order them from his website,
www.puzzleatomic.com.
In 1986, Douglas published a spiral bound book in which he tried to classify and analyse various features of circle puzzles. It contains many highly original ideas and even though a lot of it is impractical, it is fascinating. It also has several solutions to Engel's Enigma, and a section on puzzle patents.
Douglas has very graciously allowed me to reproduce the whole book
on this site. I have tried to keep it as close to the original as possible, so I have kept the
images in the same style (even though most pictures have been redrawn) and kept the same page
numbering. I have occasionally inserted a comment or correction of my own, and to be clearly
distinguishable from Douglas' original text my comments are in italics and in square brackets,
[like this - J ].

Thanks to the many people who have inspired and hypnotized me
with puzzles. In addition I wish to thank the persons who contributed
both directly and indirectly to my tome. Alexander Keewatin Dewdney
contributed indirectly by mentioning and naming the Engel's Enigma
puzzle in his 'Computer Recreations' column in Scientific American.
Jack Eidswick, a mathematician at the University of Nebraska, has used
the EE in his classes and talks and is now looking for a general solution
for rotary puzzles. His general solution for cubelike puzzles appeared
in the March, 1986, American Mathematical Monthly I recommend this
article highly to anyone wishing to understand how to solve rotary
puzzles.
[
Jack Eidswick is mentioned in Cubic Circular #2
for having made a Rubik's Cube Engagement Calendar. He has also written
Rubik's Cube Made Easy. - J ]
Father Ralph L Aschenbrenner of Solomon, Kansas contributed a solution algorithm for the EE. L. E. Hordern from Reading, England also contributed a solution algorithm for the EE. Several others have contributed solutions and I regret that I could not print all of them. Puzzles similar to the EE are being manufactured by Kelltek Plastics of Englewood, Colorado under patent 4415158. At present it looks as if these puzzles are selling well and will be useful in the community of teachers of mathematics and their dedicated students.
Lastly I wish to thank the people who have struggled to invent, build and acquire patents on rotary puzzles and have thereby created a link between the real world and the bewildering, but beautiful world of group theory.
Jack Eidswick wanted to know if I had a definition for circle puzzles. I didn't. Chapter 2 is an attempt to provide a definition for rotary puzzles in general and circle puzzles are a form of rotary puzzle.
It was necessary to find something simple and precise that would lend itself to mathematical development. Many people think of Rubik's (or Nichol's) cube as a cubic form of 27 subcubes. I think of it as a sphere sliced by six planes. An even simpler description is a sphere with a circle puzzle covering the surface. Both of these ideas seem to break down if you talk about a 7x7x7 cube where all subcubes are identified. In fact you can slice a sphere with 36 plane cuts and get a figure with identical properties. So the general cube puzzle can be built as a general rotary puzzle and the definition is fully satisfied.
Why is It necessary to have a definition of rotary puzzles? Surely any definition will be inadequate once an inventor or creative mathematician sees it. I believe that the definition is necessary to bring some order to the study of the goodly number of rotary puzzles that have been built in such a very short time. Is it not time to try and understand something about all the classes of possible puzzles? What we need is a rotary puzzle building theory. Chapter 2 is not such a theory but it is an attempt to take a first step in that direction by classifying the significant features and properties of the puzzle forms possible considering circle puzzles. For a rotary puzzle building theory to be complete you have to prove that you have classified all possible kinds of puzzles, as well as provide a general puzzle solution, and formulas for the number, and shapes of the basic pieces that make up any arbitrarily built puzzle. Chapter 2 shows, clearly, that this is not going to be easy to do.
Rotary puzzles seem to be a revolutionary idea. Ernő Rubik was by no means first with the rotary puzzle idea, but his cube was notable by becoming a mass craze and inspiring a whole basketful of cubelike puzzles. Rubik's cube was an infamous and powerful force bringing esoteric mathematical ideas into the palms of our hands. What is really amazing is that, with the incredible mass of material developed about groups, mechanical puzzles making use of some of the group theory ideas did not become popular until the cube. History may see the cube and other rotary puzzles as the first mechanical puzzles to become a necessity in the serious teaching of group theory.
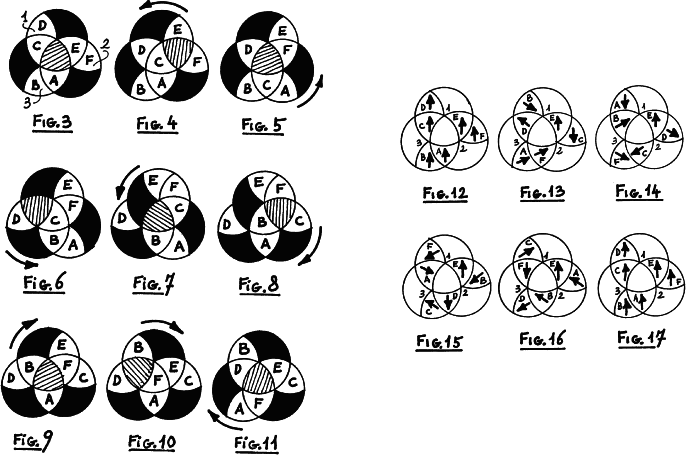
This chapter presents several algorithms for solving Engel's Enigma and any circle puzzles of a similar nature. The solutions were submitted by enthusiastic owners of the Enigma. My own method is not efficient and is intended to provide readers with a simple mnemonic for easy memorization of moves or of any algorithms a person might wish to devise.
The triangular pieces are called stones and the rectangular pieces are called bones. Use the phrase 'i can do best' to letter all but the centre bone as shown below. The centre bone is called the do focus. If the rotation o is listed it means to rotate the bone in the o position into the do focus (But don't think the symbol o has moved! Every time I say o it means the identical rotation.). If I say i it means to rotate the bone in the i position into the do focus. The result of a series of rotations causes pieces to change position or orientation or both. So the result 12 means stones 1 and 2 have changed places with each other and 1324 means 1 goes to 3, 3 to 2, 2 to 4 and 4 to 1. Result 1,3-1 means stone 1 rotates 120° clockwise and stone 3 rotates 120° counterclockwise, but their position is unaffected. The first letters of the words of a sentence will list a series of rotations. The sentence:
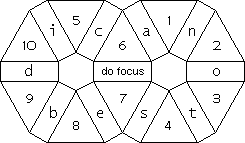
A. 'this circle trys every able crime at every nine', gives 13,
42 (stones 1 and 3 are exchanged and stones 4 and 2 are exchanged).
and,
B. 'oh, call, shout, bellow, this is sure bound on its actual
empty navel' gives 1423 and,
C. do sentence A then sentence B for 34, 2-1.
If you need to solve stones in the left circle simply rotate the puzzle so the left and right circles change places then perform the above sentences as needed. Or, to exchange any adjacent pair of stones put them in position 3 and 4, and perform C, then put them back where you got them. Use any algorithm flexibly in this manner for all sorts of exchanges.
D. 'call all extras safe', gives 15, 67. This might be handy for getting some stones located to begin with.
E. Do D twice for 5-1, 1-1, 6, 7. Or reverse D twice for the opposite effect.
F. Do C twice to get 2, 3, 4-1.
G. 'oh, ed, sell cards now, ed this end now is sure bound silly in a empty scowl coveting time', gives 1-1, 2.
With a few flexible applications of E, F, and G, all stones should be oriented properly.
F. 'this extra trap causes ten bats to itch, ten bats to coil. now call nine', gives aos. G. 'twinkle cats solve ed's o In nine but never include nasty bombs so clever ads end now', gives ast. H. 'never end a cone on bad time in the best turn in a ending show calling true', gives ans.
With F, G, and H, you should be able to position all the bones.
My method is to first solve the left circle completely. This is easy to do since enough 'parking' spots are left in the right circle so that
you can solve the left circle without need of any involved algorithms. I then solve the stones for position and then for orientation in the right circle. Lastly I solve the bones for position in the right circle and the EE is solved.
If you discover short sequences of moves for the right circle you can use the 'i can do best' mnemonic to make up your own sentences. This is an easy way to quickly memorize a complete solution for the EE.
This puzzle is solved when it forms 5 solid colored footballs with bones of another color separating the 5 footballs. First put the colored ends of the footballs together properly, disregarding the bones. This is fairly easy. Now get a football into the do focus with its bone adjacent to the top right of the football. Perform L-1, R-1, L, R, L-1, R-1, L, R. If the bone is adjacent to the top left of the football in the do focus reverse this procedure with R, L, R-1, L-1, R, L, R-1, L-1. This will insert the bone into the football. I should explain that R, R2, R3, R-1, R-2 means rotate the right circle 1, 2, 3, notches clockwise, and 1, 2 notches counterclockwise respectively. The identical meaning attaches to the L notation for the left circle.
(Note: This algorithm was provided by someone writing purely in the vernacular. He has never studied group theory and does not use any kind of standard mathematical notation. The algorithm is unique and gives some idea of how someone forges an algorithm from scratch. The first part of the algorithm was clarified a little but all notation is exactly as given by the author.)
Designate the pieces according to the EE figure shown here.
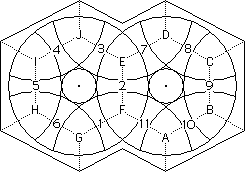
In this part of the solution the bone numbers designate the positions of the footballs. Football 5 is the controlling football. Thus football 5 tells you where we think of the other footballs in the left circle as being.
FIRST PUT THE TRIANGULAR SHAPED ENDS OF EACH FOOTBALL IN THEIR PROPER POSITION IN THE LEFT CIRCLE. For example, if the centre of the circle is light blue, put all the light blue centered pieces in the left circle in their proper place in reference to the others, so that E, F, G, H, I, J, ARE ALL IN THE PROPER POSITION, but not necessarily in the proper orientation. This is easy to do and you need no formula to do this.
The problem in the first part of the solution would be to position the remaining triangular shaped ends of the right circle. A, B, C, AND D, and to do it in such a way that the triangular shaped ends of the left circle which have to be moved in the process return to their proper places.
Example to reverse A and C. First process, mixing.
The stones are located with a mixing and restoring operation. The
mixing operation can be designated with the three footballs 1, 2, and
3. If I say "C 1, 2, 3, 2" it means to bring footballs 1, 2, 3, and 2
successively into the intersection with the left circle while rotating
the right circle one notch clockwise after each motion of the left
circle. Do C 1, 2, 3, 2.
Second process, restoring.
Only 2 methods of restoration are necessary.
1. Restore J and E, then G and F, or,
2. Restore G and F, then J and E.
First put football 3 in the intersection with the left circle, written as 3, now you Can restore J with the right circle written as J, then do 2, E, 1, G, 3, Put F in position J written as FJ, 2, turn the right circle 1 notch clockwise written as rt c1, 3, rt cc1(counterclockwise 1), 2, rt cc1, 3, rt cc2. This completes the reversal of A and C. This whole mixing and restoration process is written as C 1, 2, 3, 2, J, E = AC.
In other words restore in the order J, E, G, F in the most efficient manner possible. Use the same efficient method of restoration for all formulas given. An additional note on mixing is that if you see a formula that starts with 2 it means to turn the right circle 1 notch to begin with since football 2 is already in the centre. If a formula contains two or more adjacent 2's it means to turn the right circle 2 or more notches at that part of the formula then go to the next number different from 2 to turn the left circle.
| Stone location formulas | |
|
C 2, 3, 1, J, E = AC
C 2, 2, 3, F = AD (G already located) C 1, 2, 3, 2, G, F = BD C 3, 2, 1, 3, J, E = ADC C 1, 3, 2, G, F = ABC |
CC 2, 3, 1, G, F = AC, BD
CC 2, 2, 3, F = ACBD CC 1, 2, 3, 2, G, F = ABDC CC 3, 2, 1, 3, J, E =ADCB CC 1, 3, 2, G, F = ADB |
After you have finished part one, you have A, B, C, D, E, F, G. H, I, and J in their proper positions, but not necessarily with the part that matches the color of the circle being on the inside part where it belongs. So you work your way around the circles, getting the different corners in the centre position between the two circles, such as getting them in positions A,F,E and G. You can gradually rotate the corners into proper position, by doing maneuvers similar to this.
A to F position, then G to F position G to A position, A to G position. Then you will have A in G position, G in A position, E in F position and F in E position. ROTATE THEM AGAIN THE SAME WAY AND THEY RETURN TO THEIR PROPER PLACES, but they have each turned, A and G have rotated counterclockwise one position, F and E have rotated clockwise one position. This is called the wiggle waggle.
Using this method, I would rotate them so that first G is correct with the circle color being inside to match the circle, then I would do
it with left circle rotated one notch clockwise, and using this method, put F in its proper position, etc. until I have done as many of the left circle as I could. Perhaps at least one corner will be left in an improper position. Then placing the football nearest the improper corner in the opposite circle and using the same method, I would go around the other circle, until it has only one corner left. Sometimes a person is lucky and all corners turn correct. But usually a person is left with two corners incorrectly rotated. How can they be rotated without disturbing the other corners? FIRST YOU PUT THEM IN POSITION F and E.
Then do the wiggle waggle motion as indicated in paragraph 2 above, so that all corners are back in their proper position but rotated, A and G counterclockwise one position, and F and E clockwise one position. Turn the puzzle upside down and use the wiggle waggle motion with J, D, E and F.
Then use the wiggle waggle motion with A, F, E, and J and then with G, F, E, and D. Then A, G, J, and D will be back in their proper orientation, but E and F will have rotated one notch. If still not in the right position, repeat the process one more time.
NOW YOU SHOULD HAVE ALL THE CORNERS IN THEIR PROPER POSITION AND THEY SHOULD ALL BE ROTATED PROPERLY TO MATCH THE COLOR OF THE INNER CIRCLES, BOTH LEFT AND RIGHT CIRCLES.
Now you need to move the insides of the footballs into the proper
football with the color in the proper direction.
To do this, now use the numbers, not only to identify the football.
but also to identify the inside part of each football.
Turn the circles in such a way that the piece you wish to go into
position 3, is in position 2.
Then wiggle waggle A, F, E, and J, two motions so they return to
their own spot. Then wiggle waggle D, E, F, and J, two motions so
they return to their own spot.
Then wiggle waggle A, F, E, and J, four more motions.
Then wiggle waggle D, E, F, and J, four more motions.
You will find 11 and 7 have changed places, and 2 and 3 have changed
places.
Using this method over and over on both circles, you gradually come to the final two that need to be changed. During the process, you will have finished one circle to the point that the pieces 1 and 3 which match each other, change positions or the pieces 7 and 11 which match each other, change positions but it doesn't matter because they are exactly the same color. So after getting one circle finished, you can turn the last circle gradually to each position without further messing up the finished circle.
After solving the EE a few times using this algorithm you will discover several time and eye saving shortcuts.
(Note: L. E. Hordern has one of the world's finest and largest
collections of mechanical puzzles. He derived this algorithm after
owning his enigma for less than 2 weeks.)
[
There is a short wikipedia article about the late Edward Hordern.
- J ]
The puzzle has 21 movable pieces shown by the solid lines in the figure. The dotted lines show the areas of colour which extends onto the border as well as the centre circles. There are 10 triangular shaped stones numbered 1-10 and 11 rectangular shaped 'bones' numbered a-k in the figure. Numbers and letters refer to both pieces and positions. A stone or bone is in its 'Home' position when it is correctly placed but not necessarily correctly oriented,
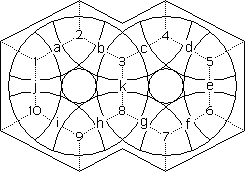
|
L = rotate the Left ring one step clockwise
Ra = rotate the Right ring one step anticlockwise La2 = rotate the Left ring two steps anticlockwise | |
|
L1 = L, Ra, La, R
L2 = La, R, L, Ra L3 = L, Ra2, La R2 L4 = L, R, La, Ra L5 = La, Ra, L, R (L1)2 = do L1 twice. |
R1 = Ra, L, R, La
R2 = R, La, Ra, L R3 = Ra, L2, R, La2 R4 = Ra, La, R, L R6 = R2, L2, Ra, La2, Ra2 |
| Note that, apart from R6, the second two moves always reverse the first two. A 'Process' is a combination of the above sequences of moves. | |
SOLUTION
A slew of puzzles such as Rubik's Cube, Alexander's Star, and Engel's Enigma can be classified as rotary puzzles. I will not explain exactly why these puzzles are rotary puzzles. This is a puzzle and you will have no trouble figuring it out after you read this chapter.
The concept of the rotary puzzle is so simple and easy to understand that almost anyone can grasp it by reference to a few figures and examples. It does not follow that rotary puzzles are easy to solve. It can even be a good little puzzle trying to figure out if a given puzzle is a rotary puzzle. In this chapter you may read definitions and look at examples in any order.
I have attempted to list circle puzzle properties based on significant features of geometry and symmetry. The problem with this is that the rotary puzzle idea is so plastic that one can build a puzzle with as many properties as one wishes to endow it with. The idea, then, is to make each property as separate and independent as possible. One may then describe a puzzle by listing its significant properties.
The big problem with 3D rotary puzzles is that they form too large a slew to discuss in a meaningful way in this book. Perhaps the examples presented will interest readers enough to encourage further experimentation in the direction of 3D rotary puzzles.
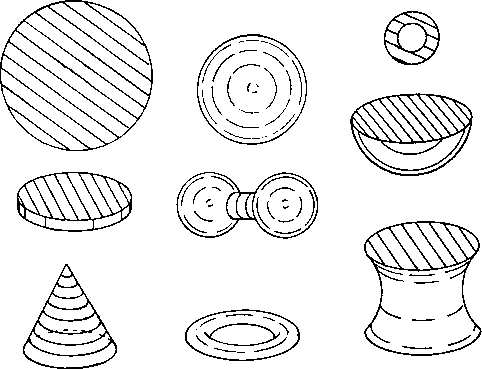
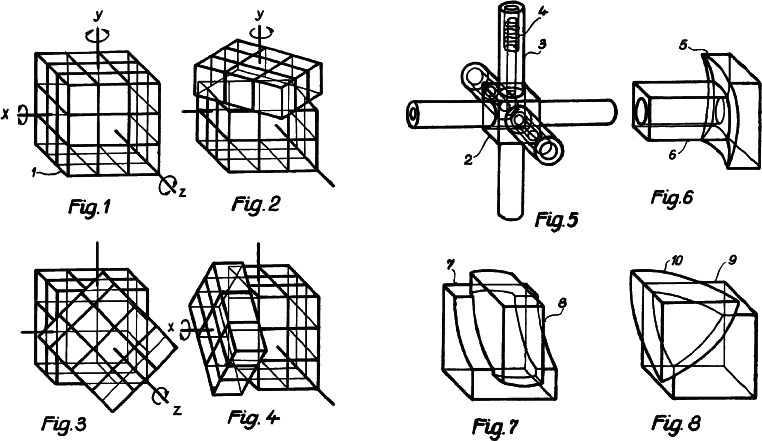
In order for a rotary figure to be part of a rotary puzzle it must be possible to rotate the figure about some axis without disturbing the surrounding space. If a square cookie were surrounded by jello it could not be rotated in any manner without cutting through some of the jello. If the cookie is circular it can be rotated about 1 axis without disturbing the jello. If the cookie is a sphere it can be rotated about any number of axes without disturbing the jello. In 2D only circles and annular rings seem to qualify as rotary figures. In 3D many kinds of figures can be used.
Rotary figures that satisfy the jello requirement in 3D are cylinders. spheres, cones, tori. ellipsoids. oblate spheroids, egg shapes. barbells. sliced spherical layers and so forth.
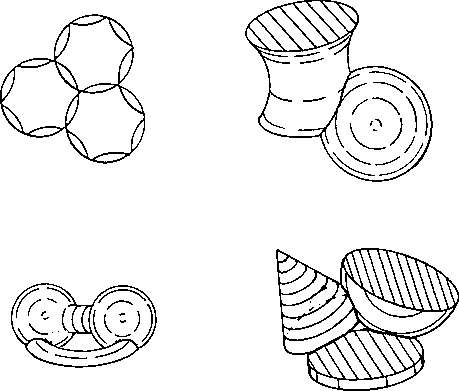
A rotary puzzle is built from 2 or more rotary figures that intersect somehow in their common space. Where 2 rotary figures intersect they dissect out a piece common to both rotary figures. Each rotary figure may be further subdivided into a number of pieces by curved borders with no voids between the curved borders.
The pieces of a rotary puzzle are always and only moved by alternately rotating the rotary figures.
A rotary puzzle is one where each and every curved border of each and every piece can be made to slide against one or more curved borders of other pieces or against the surrounding space by alternately rotating the rotary figures.
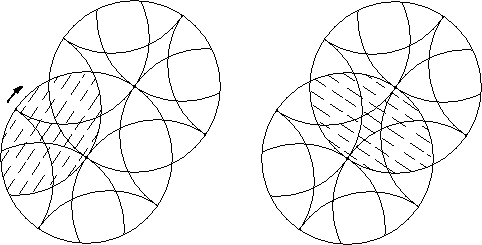
An intersection that leaves both rotary figures alternately rotatable is a valid intersection.
An allowed rotation is a rotation of a rotary figure that then allows at least one intersecting rotary figure to rotate.
[ This circle puzzle has been produced as Rashkey. See my Rashkey page. - J ]
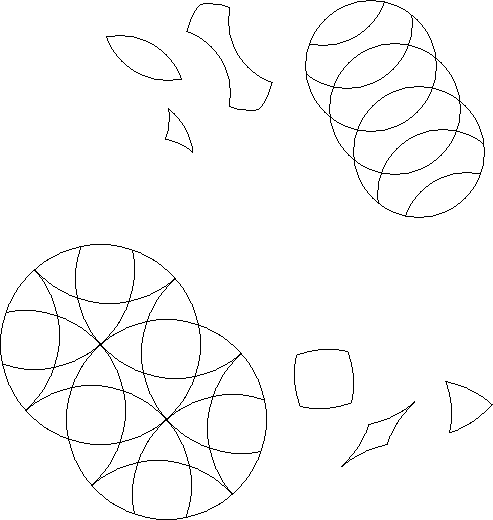
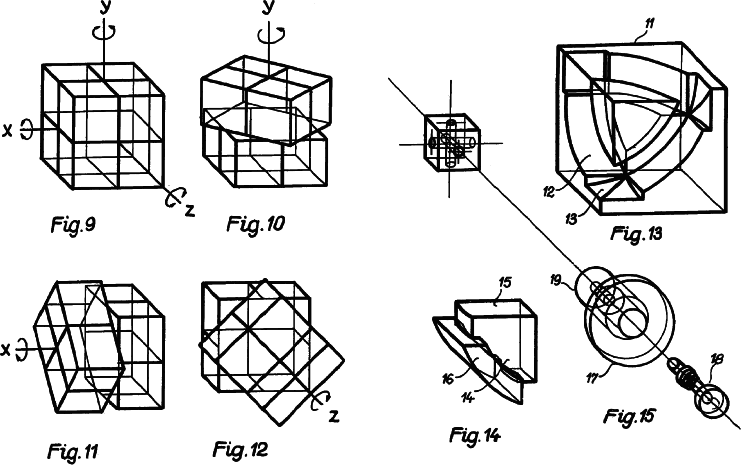
The single representative of all congruent pieces in a rotary puzzle is a basic piece of that puzzle. The number of basic pieces is a rough measure of the puzzles complexity.
An orbit of a basic piece is all positions that can be occupied by that piece. All congruent pieces need not belong to the same orbit.
The multiorbit of pieces is the combined orbits of all selected pieces.
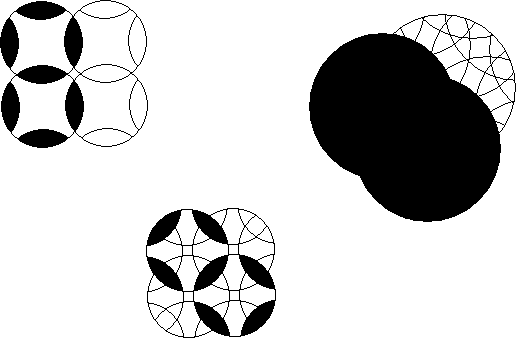
The mutualsection of the intersection of a pair of rotary figures in a rotary puzzle is the orbits of the pieces in the intersection confined to those 2 rotary figures only.
A multisection of an intersection of a pair of rotary figures in a rotary puzzle is the complete puzzle orbits of all the pieces in the intersection.
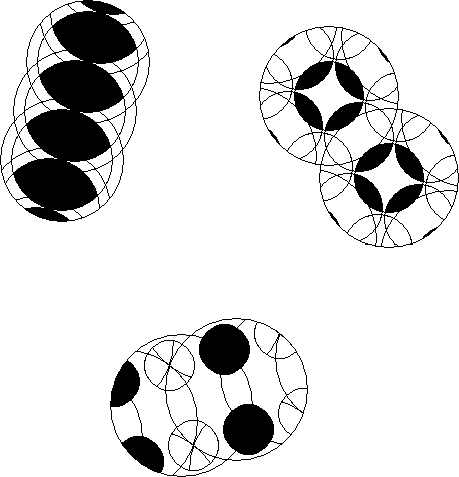
The orbital path of a basic piece is the line segments connecting the centres of the successive positions of the piece. The line segments are gotten by the smallest possible allowed single rotations. Degenerate paths are possible by making larger single rotations or combining 2 or more rotations. All degenerate paths can be accessed from the longer orbital path. You can determine a cycle path of a set of repeated rotations by making a drawing. The cycle path does not give the cycle length or the number of rotations needed to get back to a starting position by continually performing the same set of rotations. If orientation is considered the number of orbital paths of a piece is the same as the number of possible orientations of that piece that can be gotten by alternate rotations of the rotary figures.
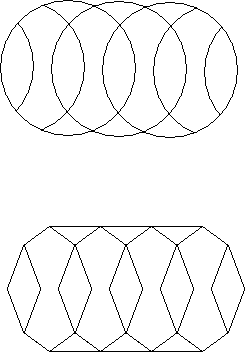
The straight line drawing of a circle puzzle is gotten by connecting vertices, (and midpoints of arcs where necessary) with straight lines instead of curved lines. This drawing is sometimes useful when curves are difficult to draw such as in a computer program.
Circle puzzles are rotary puzzles confined to 2 dimensions. The only Physically buildable ones known are those confined to a flat plane and those confined to the surface of a sphere.
Circles and annular rings are the only rotary figures that can be used to make workable circle puzzles. A puzzle could be made where a figure could not rotate a full 360° but this would not fit our definition of a rotary puzzle. In most cases puzzles like this would fit into a theory of limited rotary puzzles
The rules for making circle puzzles are given by the definition of rotary puzzles. The properties listed here are accompanied by examples in the form of figures.
Annuli and circles can be mixed for some very interesting combinations. If the inside of an annulus is rotatable it is no longer called an annulus but a pair of concentric rotary circles.
The term 'rotary circle' must be used to avoid confusion with the cutting circumferences of circles and circular arcs. The term 'rotary annulus' is used to distinguish these figures from the cutting circles of the annulus.
The examples given here do not fully cover the properties of circle puzzles A full investigation of these devices may take many years.
The most common and Interesting circle puzzles are those based on the symmetries of the periodic plane These may be classified according to the 17 plane groups lasted in many books on crystallography Puzzles based on non periodicity such as a pair of Incommensurate grads lead to an Infinity of different finite circle puzzles or one puzzle with an Infinity of circles with slightly different properties at every location.
A theory exists concerning the building of rotary puzzles as opposed to the group theory used for their solution The building theory is characterized by 4 basic operations: 1. adding a rotary figure or curved dissection to a puzzle, 2. deleting a rotary figure or curved dissection, 3. changing (enlarging, shrinking, etc ) a rotary figure or curved dissection, 4. moving a rotary figure or curved dissection. Each of these operations must leave a workable puzzle so that the removal of a circle may entail many other changes These organic building changes are the rotary puzzle building theory. Change puzzle A into puzzle B by changes C(A)=B. Then if changes C2(B)=A then C2=-C where the minus means changes exactly opposite to C.
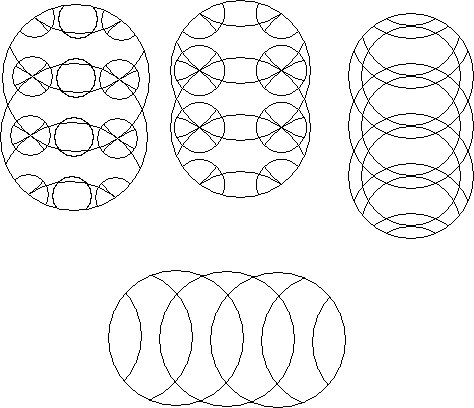
When a circle puzzle may be repeated an infinite linear distance it is line periodic.
The most common and interesting circle puzzles are those based on the symmetries of the periodic plane. These may be classified according to the 17 plane groups listed in many books on crystallography.
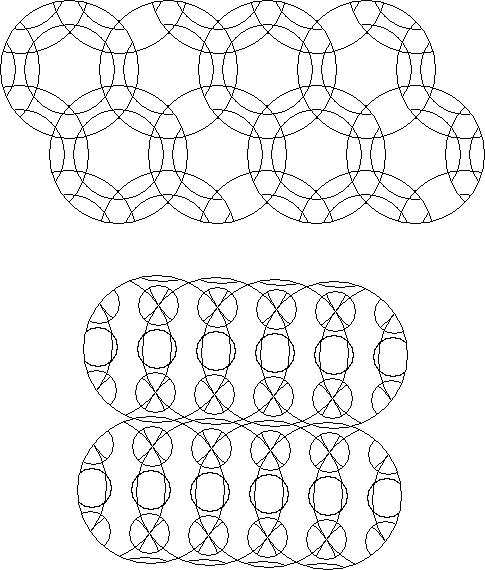
A circle puzzle that may be repeated to cover the infinite plane is called a plane periodic circle puzzle. A periodic circle puzzle is any circle puzzle that can be dissected out of a repeated circle puzzle tiling that includes one or more of each different type of repeated circle in the tiling. The centres of the rotary circles and the centres of the circular arcs of a periodic circle puzzle form a periodic grid of points.
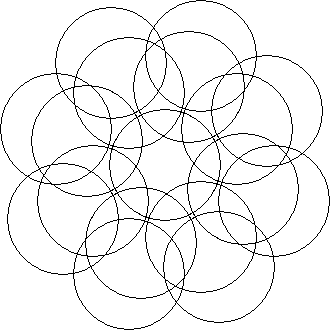
Puzzles based on non periodicity such as a pair of incommensurate grids lead to an infinity of different finite circle puzzles or one puzzle with an infinity of circles with slightly different properties at every location.
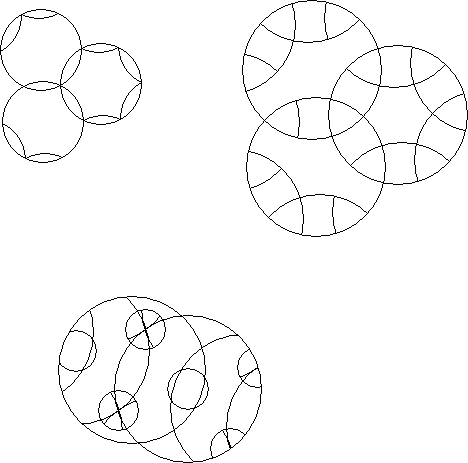
A circle puzzle where every rotary circle contains a dissection that has symmetry by some fractional rotation of the rotary circle is a locally symmetric circle puzzle. It must not be possible to destroy the symmetry of any single rotary circle by an allowed rotation of a rotary circle. Many examples are possible.
A locally symmetric circle puzzle where every circle contains an identical dissection is globally symmetric
A circle puzzle that has at least one position where every rotary circle contains a dissection that has symmetry by some fractional rotation of the rotary circle but where this symmetry in at least one rotary circle may be destroyed by an allowed rotation of an intersecting rotary circle is a partially symmetric circle puzzle
A circle puzzle where the entire circle puzzle is symmetric by reflection across a line of symmetry.
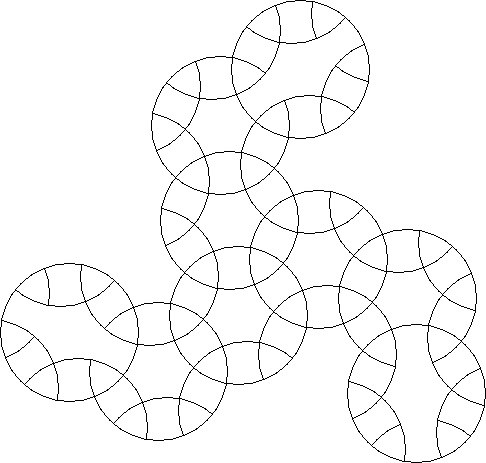
A circle puzzle where the entire circle puzzle is symmetric by a fractional rotation about a point.
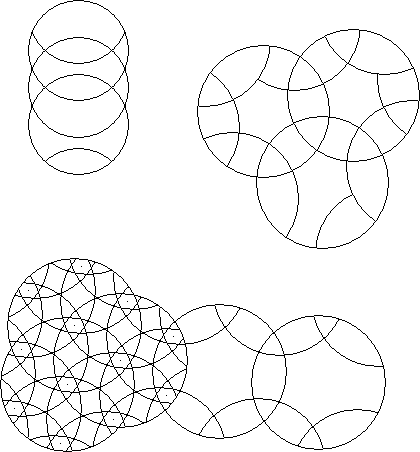
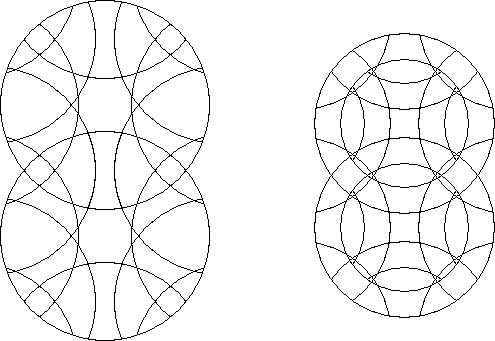
A circle puzzle where every rotary circle has equal radius is an equal radius circle puzzle.
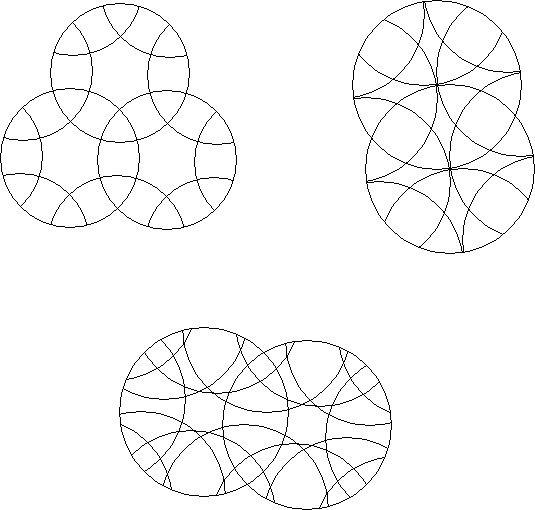
If every intersection of two rotary circles in a circle puzzle is of equal depth then the puzzle is an equal intersection circle puzzle.
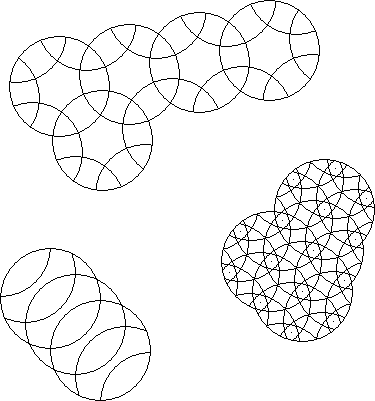
A globally symmetric, periodic, equal intersection, equal radius circle puzzle is a regular circle puzzle. One infinite family that is line periodic exists. Four plane periodic infinite families with 60°, 90°, 120°, and 180° symmetry exist. On the surface of a sphere you can have the 5 types of puzzles with the symmetry of the faces of the 5 regular solids, tetrahedron, cube, octahedron, dodecahedron, and icosahedron, and one linear type that goes around the equator of the sphere.
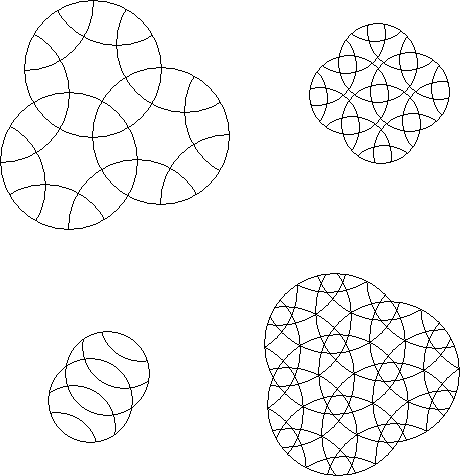
A regular circle puzzle where the fewest number of rotary cities is used that can fully express the pieces as to their position and orientation with respect to the circle puzzle is a basic circle puzzle. The same examples as in the regular circle puzzles exist except that, for instance. in the Euclidean hexagonal (60°) symmetry version you would be limited to 3 intersecting rotary circles which is an infinite family of basic circle puzzles. The Engel's enigma is not a basic circle puzzle since it does not have the third circle.
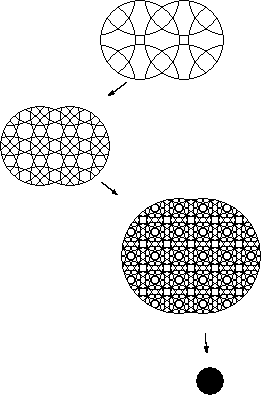
By allowing the distance between the centres of the rotary circles in a basic circle puzzle to approach zero you get an infinite number of pieces. The resulting perfect black circles can do weird transformations. For instance you could draw an asymmetrical figure on one. then by an infinite number of manipulations turn the figure into a close approximation of its enantiomorph.
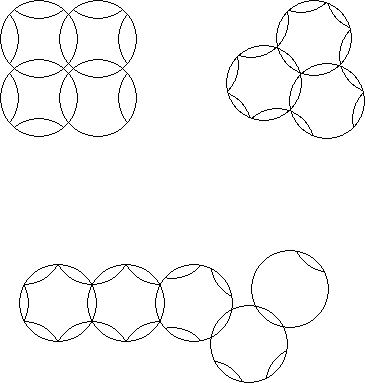
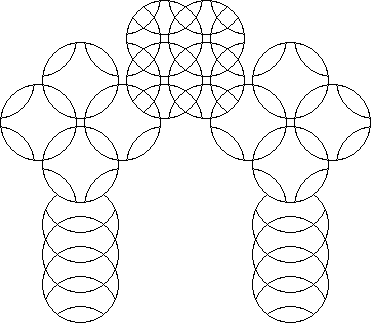
A circle puzzle where every intersection of 2 rotary circles contains only 1 piece and the depth of cut does not extend to the: centre is an undercut circle puzzle. These puzzles can have many fractional symmetries not possible where 3 or more rotary circles intersect.
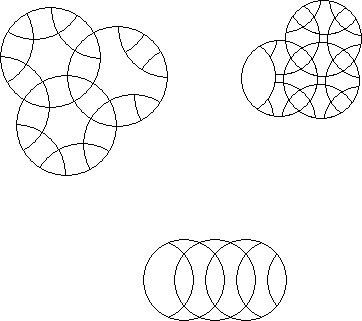
When the intersection of each pair of rotary circles contains more than 1 piece, but does not extend to the centre of the rotary circles, an overcut circle puzzle results.
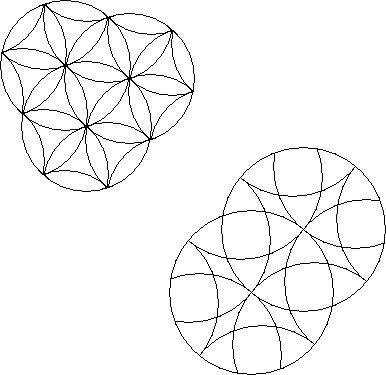
If the circumference of each rotary circle passes through the centre of the rotary circle it intersects, the puzzle is a centercut puzzle.
[ A two-circle version of the top puzzle is called the Cohan Circle. See my Cohan Circle page. - J ]
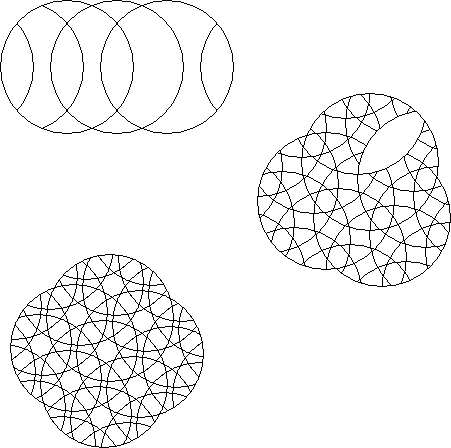
A circle puzzle where the circumference of each rotary circle extends past the centre of the rotary circle it intersects is a deepcut circle puzzle.
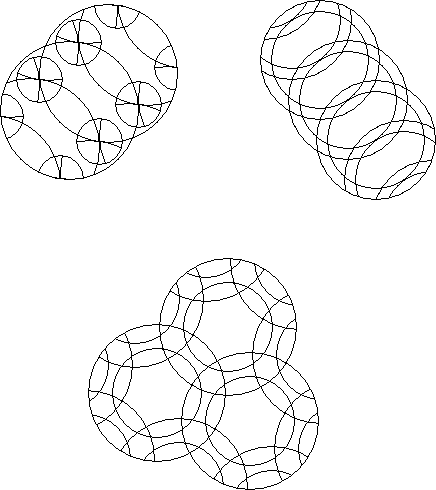
Multicut puzzles contain more than one type of cut such as undercut and overcut.
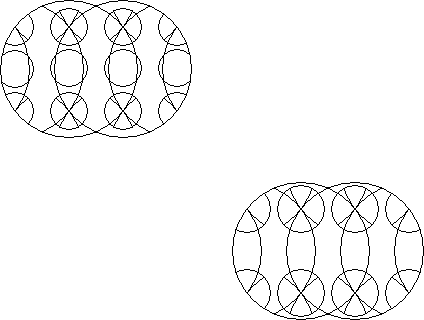
An included circle circle puzzle is a circle puzzle where at least one of the rotary circles entirely contains another, smaller but not concentric rotary circle.
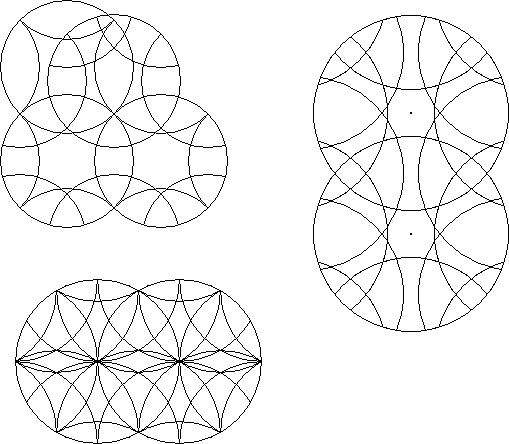
A hybrid circle puzzle results when a circle puzzle: with one symmetry is overlaid by another puzzle containing an equal number of rotary circles but with another symmetry and all the rotary circles coincide exactly. For instance the Engel's enigma could be overlaid with a pair of circles that have 90° symmetry. The resulting hybrid puzzle could be operated as both kinds of puzzle.
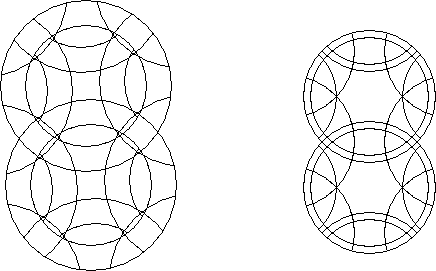
An included puzzle circle puzzle is a circle puzzle that can be seen as containing a separately identifiable circle puzzle inside it. The included puzzle can itself be an included puzzle circle puzzle.
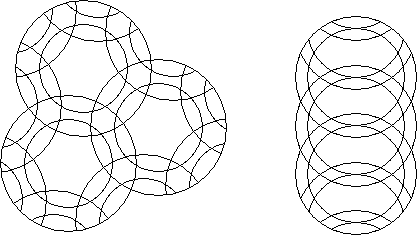
A circle puzzle where at least one of the rotary circles contains a smaller concentric rotary circle is an concentric circle circle puzzle
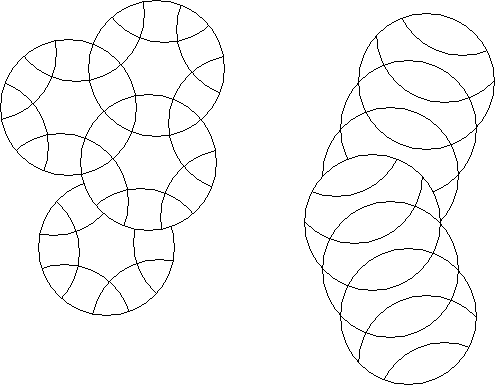
An offset circle puzzle is one that has no position where all rotary circles are crossable for rotation.
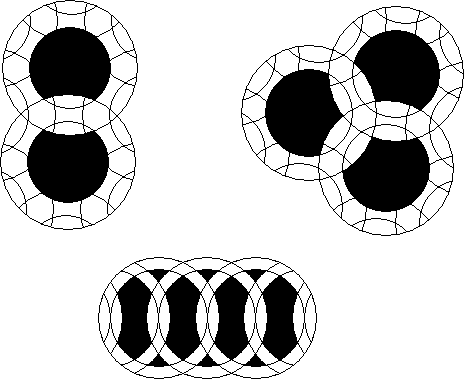
Annulus puzzles are made from annular rings instead of circles. When annuli are mixed with circles the resulting puzzles are annular circle puzzles.
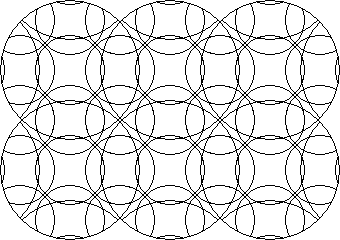
A circle puzzle where the grid of the centre points of one circle arrangement coincides periodically with the grid of the centre points of another circle arrangement.

A circle puzzle based on a pair of offset grids that are equal and have their grid axes parallel.
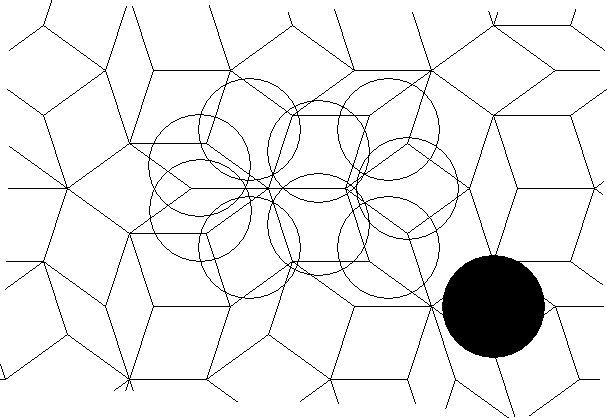
Penrose circle puzzles are based on the non-periodic grid gotten from the centres of the figures used to make a Penrose tiling (see bibliography). These circle puzzles would have some similarity to a standard non-periodic circle puzzle. A significant difference is that only a small, finite number of differently dissected circles would be needed to make the infinite puzzle. Some of the circles would appear to have full five fold symmetry.
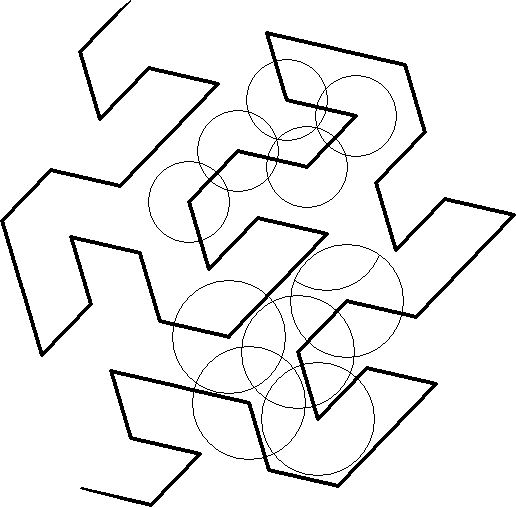
The example shown here merely produces either hexagonal or triagonal symmetry puzzles. But frontal circle puzzles can be based on any grid gotten with a frontal and by using different sized circles to match the edges of the frontal curve some interesting puzzles might be possible. This beginning of a frontal curve is by W. Gosper (see Martin Garner's December 1976, Scientific American column).
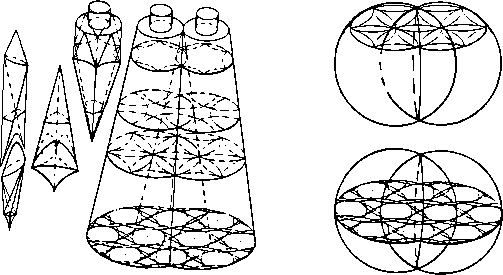
A large cornucopia of weird puzzles exists when different kinds of figures, such as spheres, cones, barbells, etc., intersect. Puzzles formed of like figures such as intersecting cones, or intersecting ellipsoids also form a large class. If we require that a rotary puzzle be kept simple to solve then it is necessary to make the puzzle fairly symmetrical. A partially symmetrical puzzle such as a hybrid puzzle can be more difficult to solve than a symmetrical one with the same number of pieces.
Many of the significant types of circle puzzles have their counterparts in sphere puzzles. These are gotten by replacing the 2D concept with its appropriate 3D analogy using spheres instead of circles. By using the space groups of crystallography many sphere puzzles can be simply classified.
1. Any pair of rotary puzzles may be allowed to intersect in any manner and the result will always be another rotary puzzle.
2. In a deepcut puzzle, as the cut gets very deep, only a small sliver of pieces is left unchanged with each rotation Many rotations are therefore required to mix the puzzle up greatly. The solution of this type of puzzle is thought to require many rotations, because of this slow mixing principle, and providing the puzzle has been fully mixed up before solving. On top of this, a bunch of moves may actually accomplish more mixing than solving of the puzzle, if one makes a few mistakes. This is because a single piece out of kilter can require much new mixing to get it in an appropriate position to head back to a final solution.
The method of solving a deepcut puzzle would, in general, require a computer. The same kind of mixing rate process can be observed in colliding vortexes of gas or liquid. At the scale of subatomic processes the smoothness of both space and time disappears. Space and time become quantized. It is no stretch of the imagination to thank of mixing processes as quantized somewhat like a circle puzzle in these subatomic worlds. Assume that when a certain position occurs a deepcut cycle puzzle becomes unstable. It is a radioactive puzzle. But if it is sufficiently deepcut untold quadrillions of rotations will be required before the blowup position occurs. In this case it has a long half life
3. Non-periodic circle puzzles containing many circles would be difficult to solve. When the pieces are mixed up the puzzle becomes asymmetric and the solution involves recognizing dead end rotations where the permutations can not lead back to a. solution. The asymmetrically mixed pieces could create a situation where the puzzle might become almost completely locked or where rotations were fairly limited. Then each further rotation might make the situation worse requiring a backing out process. Is there more than one path to a solution once such a puzzle has been asymmetrically mixed? Or are there only a few paths each quite difficult to find? Does one end up asymmetrically locked so that he can not get back to symmetry without knowing the moves that got him locked? If he does get back to symmetry how does he then solve the symmetrically mixed puzzle?
4 Is there an algorithm for solving a complicated random circle puzzle? Such a puzzle may contain symmetrical subpuzzles. The solution algorithm would require a fairly complete knowledge of the mixing and locking process and might require a method of searching by making trial rotations.
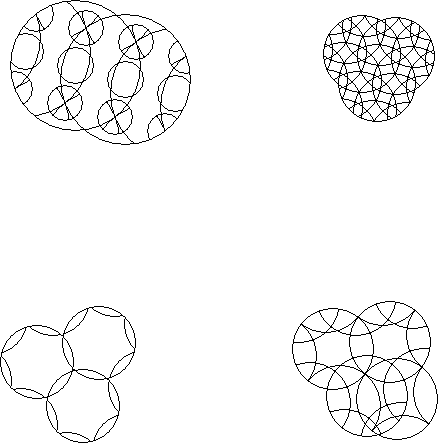
Describe the puzzles above according to significant features.
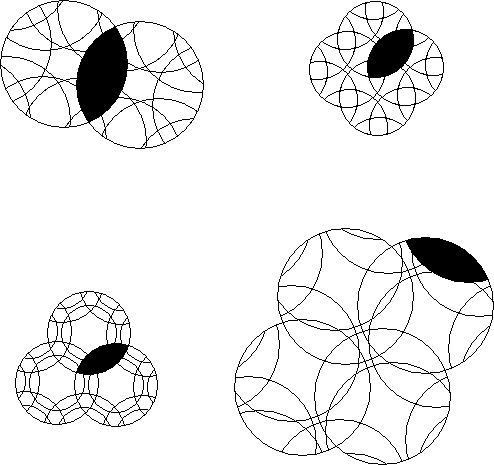
Specify the rotations required to get from a to b and from c to d.
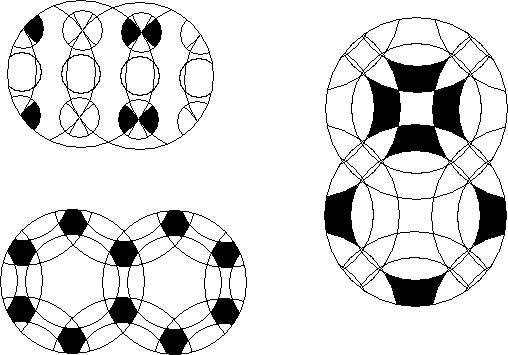
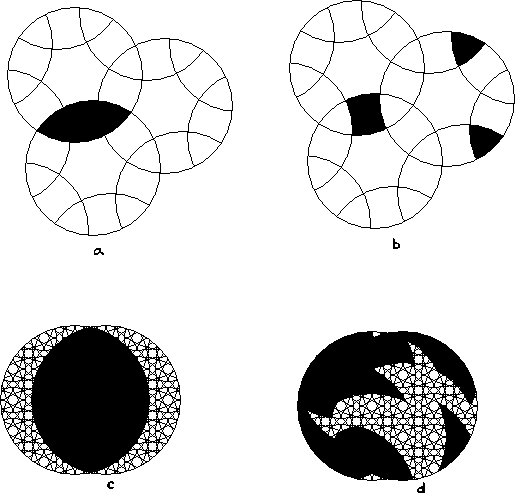
Show the rest of the mutualsection of intersection of the blackened areas.
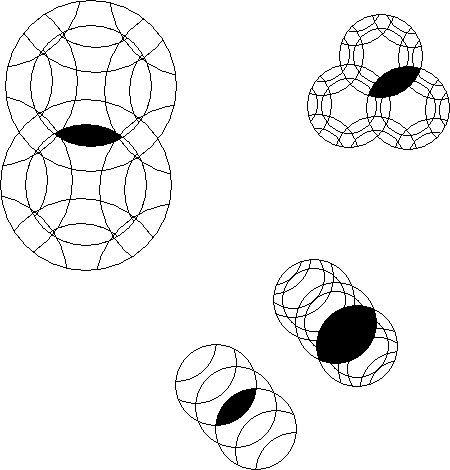
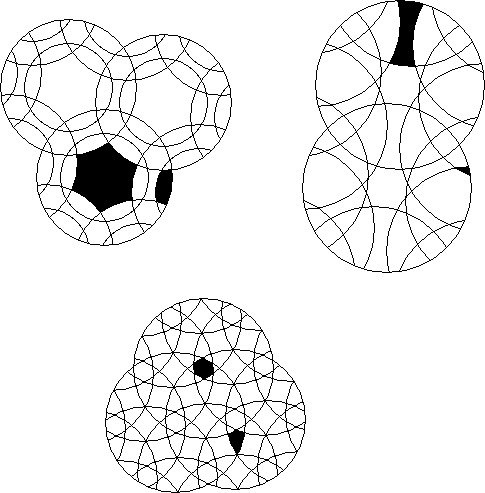
Show the rest of the multisection of intersection of the blackened areas.
Blacken the rest of the orbits of the blackened pieces.
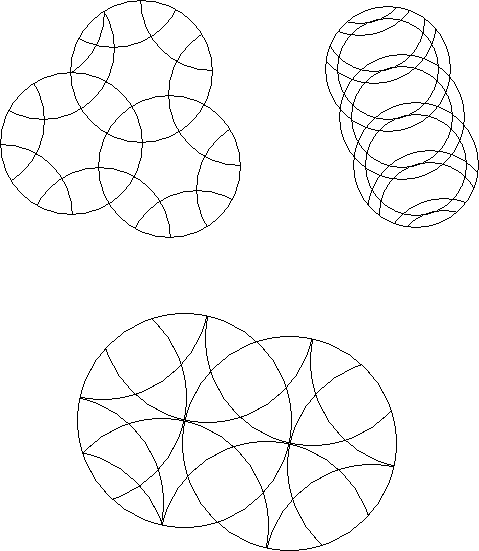
Which of the above are not circle puzzles?
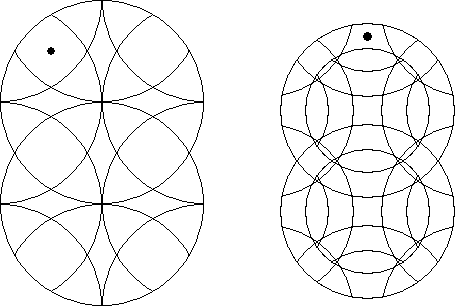
Draw the orbital path of the indicated pieces.
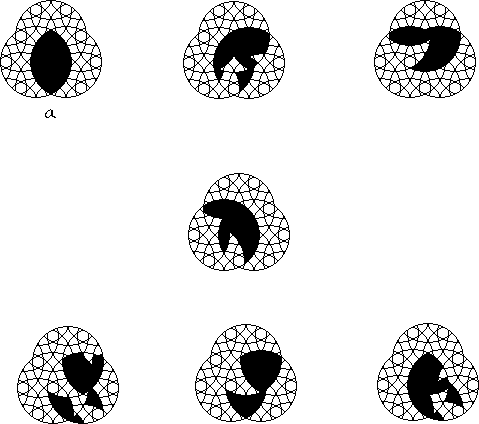
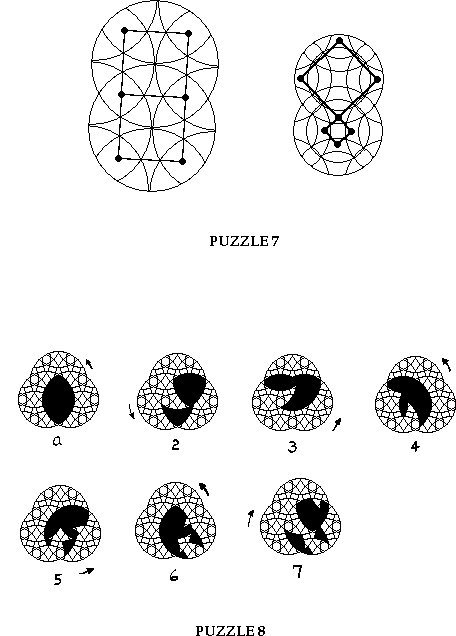
The sequence of figures above has been mixed up except for a. Can you give the correct sequence of rotary mixing of the blackened intersection?
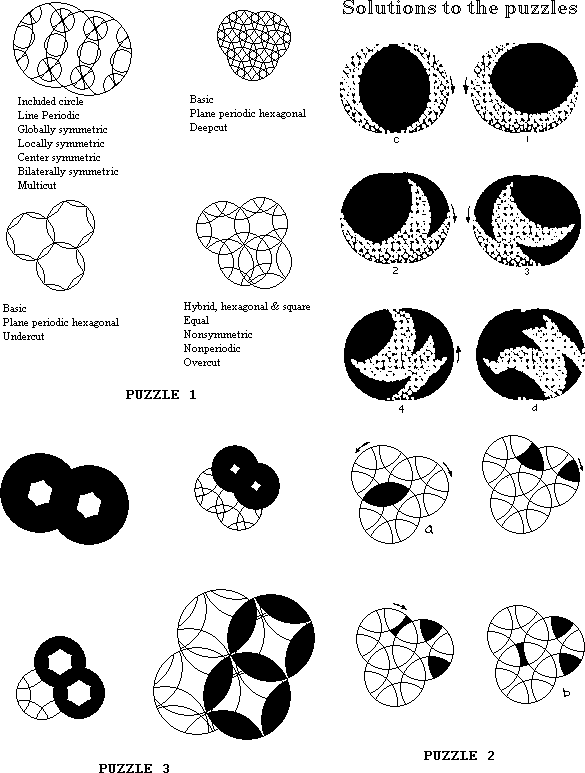
The definition of a rotary puzzle requires that all borders of all pieces be usable. In the a and c figures an extra arc has been added that is completely useless.
Patents are expensive and difficult to get. If you have made money from a patent you probably believe in the system. If you've lost money you probably see it as the biggest hoax ever perpetrated on man by man. Patents that are likely to make money are those that represent basic advances in any field. Yet the patent law says that basic principles are not patentable. You can only patent some application of basic principles. By this means the patent office hopes to encourage practical, workable devices and discourage any attempt to control a field such as electronics. The patents on rotary puzzles are a nice example of this principle at work.
The 1899 patent by Hiester A. Bowers of Reading, Pennsylvania seems to be the first one that makes use of intersecting circles that are able to rotate independently. It consists of 4 intersecting circles with 90° symmetry and a single piece contained at each intersection. Puzzles like this were probably inspired by the famous 15 puzzle invented by Sam Loyd. This 4 circle patent contains the basic germ of all rotary puzzles. Bower's puzzle is fairly easy to solve and seems to be aimed at the children's toy market. I do not know if it was ever commercially produced.
Perhaps Bowers was ahead of his time because the next patent does
not appear until 62 years have elapsed. The 1961 design patent
190,660 by Robert G. Mote of San Bernardino, California is not a rotary
puzzle. This device is simply a jigsaw puzzle with the pieces formed
from centre cut hexagonal symmetry circles. A base if provided for
holding the pieces and it is obvious that when the pieces are in place
the puzzle could be operated as a rotary circle puzzle. The design
patent does not pursue this aspect. It is the first appearance of an
overcut puzzle.
[ Continued on page 68. - J ]
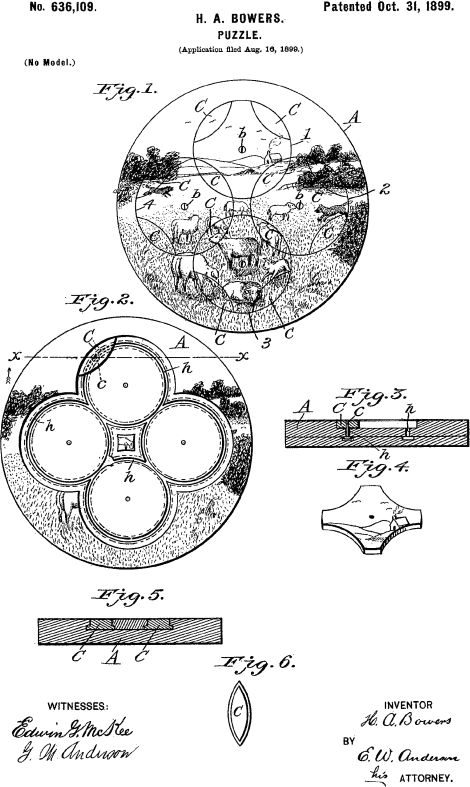
This October, 1899 patent by Hiester A. Bowers of Reading Pennsylvania is the first circle puzzle patent It contains the basic idea of all rotary puzzles.
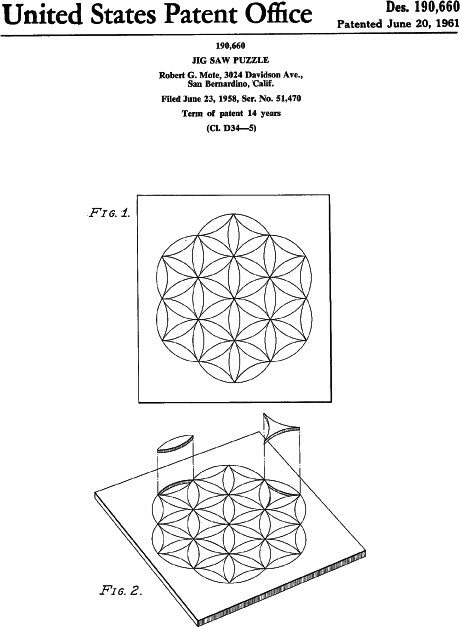
Robert Mote decided to get a design patent on this centre cut jigsaw puzzle. His 1961 patent could be operated as a rotary circle puzzle.

These figures show a circle puzzle in the form of a game board The pieces may be removed and repositioned. The 1972 patent by Daniel H. Pierson has no overcut circles.
The next rotary circle puzzle comes from Daniel H. Pierson of Sloatsburg, N. Y. in 1972. Pierson presents his puzzle as a game board apparatus and seems to overlook the puzzle aspect. His patent is the first to use different sized circles. All the drawings present undercut rotary circles.
Larry Nichols, a Massachusetts inventor, got a 1972 patent for a cube puzzle like Rubik's cube. Nichols filed suit against Ideal Toys. U. S. maker of Rubik's 1977 cube. Jerry Slocum, owner of the worlds largest collection of mechanical puzzles testified in the case which was won in October, 1984 by Nichols and is now under appeal by CBS, the owner of Ideal Toys. A U. S. district judge in Delaware had agreed with Slocum that the object of the puzzle was the same as Rubik's and issued a 50 page verdict ruling in Nichols favor. Nichols cube probably makes use of magnets to hold the subcubes together. Here is a basic difference.
Rubik took a different approach and made his cube seem magic by using internal protrusions to hold it together. His invention is an advance over Nichol's. But when a previous patent exists that accomplishes the same object it takes precedence if the object itself is new. In other words Rubik would have to wait out the term of Nichol's patent before his advanced patent could take precedence. This case clearly illustrates the complexity and intertwined nature of the patent and invention process. Each new invention should represent some advance or new approach, no matter how slight.
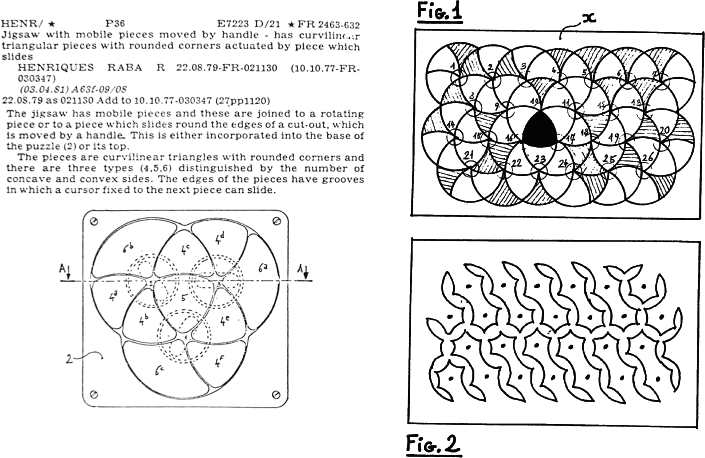
A 1979 French patent by Raoul Henriques Raba presents centre cut
circles and is clearly meant to be used as a puzzle. Raba also includes
the possibility of building his puzzle on the surface of a sphere so that
the circles have their centres on the vertices of an icosahedron. Raba
made further improvements to his invention in a 1981 French patent.
This patent incorporates many novel features. The pieces are formed so
that sometimes only one circle may be rotated. In another
embodiment a handle is constrained to move along a track limiting the
motion of the rotary circles. Raba included means for holding the pieces
in a frameworks and rotating the circles from above or below by knobs
attached to the centre cut pieces. His patent is fairly comprehensive.
[
Raba's "Taquinoscope" puzzle was produced by Pentangle under
the name Rotascope. See my Rotascope page. - J ]
A Japanese patent 55-3956 was presented to inventor Terutoshi
Ishike in 1980. This was Ishike's third attempt and is identical in
object to Rubik's cube. A different approach and an indication of the
generality of rotary puzzles comes with the appearance of the 1981
[ Continued on page 78. - J ]
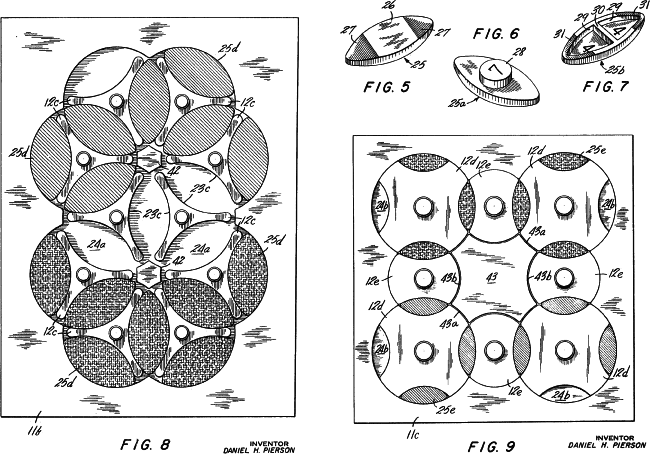
In these figures Pierson shows new embodiments of his invention. He gives the first example of a puzzle with 2 sizes of circles.
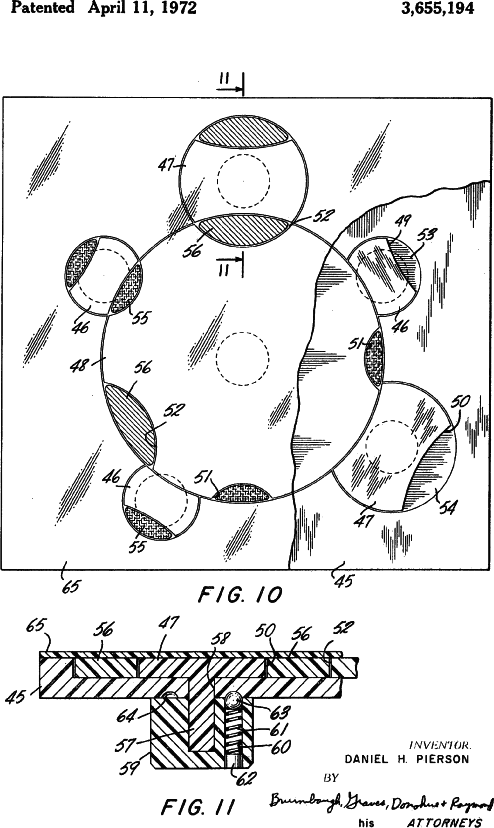
This figure shows a common technique for holding the circles in alignment with a ball and spring. The device incorporates a cover and knobs for turning the circles from the back. This is the first puzzle using 3 sizes of circles.
The classic Ernő Rubik cube patent was granted in 1977. Rubik designed a beautiful internal means for holding all the subcubes in place. He did this originally because he thought it would be a good exercise for his students to try and figure out what held it together. He soon realized that the solution to the mixing puzzle was more difficult than figuring out the internal mechanism.
Here Rubik shows his method for building a 2x2x2 cube. It seems to be similar to the 3x3x3 mechanism except that the corner cubes cover the entire external surface.
Raoul Henriques Raba got this 1981 patent covering some sophisticated centre cut circle puzzles His is the first patent to take advantage of oddly dissected pieces so that many moves are limited, increasing difficulty.
Raba was very thorough and provides these figures showing some of the positions possible with one embodiment. In his earlier 1979 patent he does not give nearly as many figures.
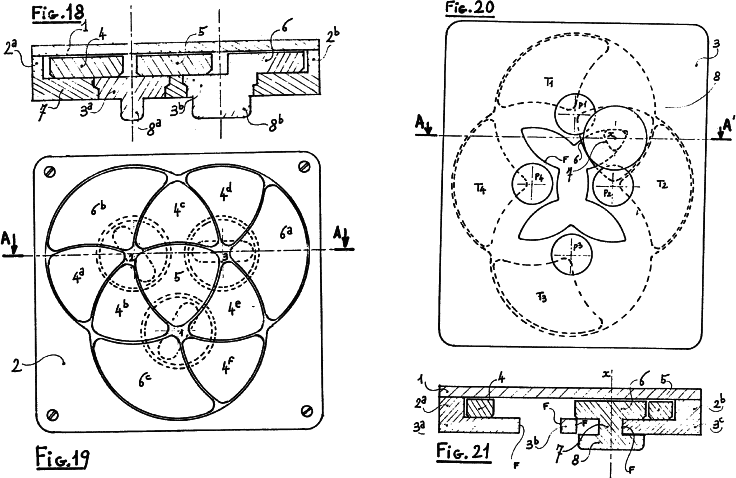
These figures show the knob mechanism for turning the circles. The knob in Figure 18 is part of one of the centre cut pieces. In Figure 20 the pieces are constrained by a kind of 4 leaf track and a knob that slides in the track
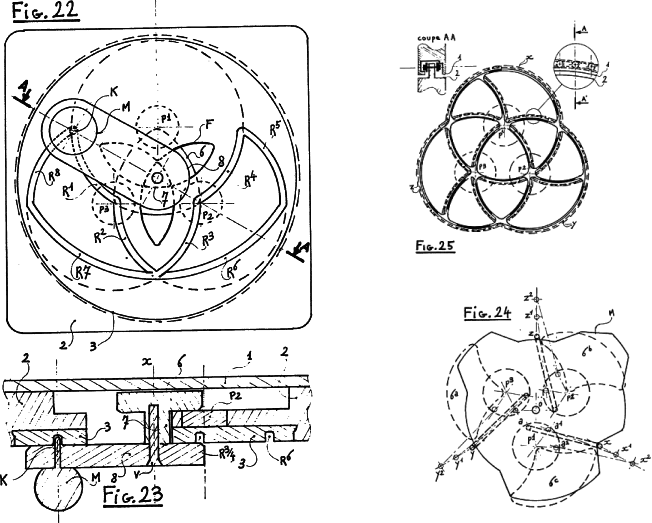
Here figures 22 and 23 show the Raba mechanism for confining movement by an extra knob made to slide in a grooved track This technique seems unnecessarily complicated The solver is required to monitor the motion of 2 objects in 2 different directions
Terutoshi Ishike had the misfortune of being a little too late with this 1980 patent for a cubelike puzzle identical to Rubik's cube. This was Ishike's third patent granted for cubelike puzzles.
German patent 8104382 by Dr. Walter Moll. This patent shows a tetrahedron and dodecahedron sliced on planes parallel to the faces.
I could not discuss rotary puzzle patents without including my own U. S. patent 4415158 granted in 1983. My patent discusses many forms of rotary puzzles and concentrates on overcut, symmetrical circle puzzles. This patent also includes methods of coding and creating topological puzzles with circle puzzles. Rubik's patent also mentions coding devices but only as a possibility. My patent is the first to show intersecting spheres.
If history is any example we will not soon see the end of new patents on rotary puzzles. The field presents practically unlimited potential for creating educational devices that both enlighten and entertain.
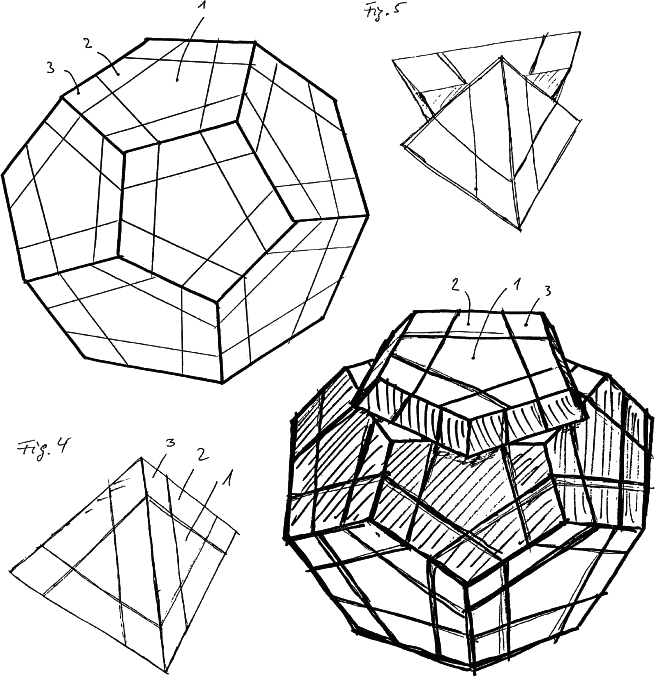
Dr. Walter Moll makes a stab at generality for cubelike puzzles with this 1981 patent. Both puzzles are regular solids sliced on planes parallel to the faces of the solids.
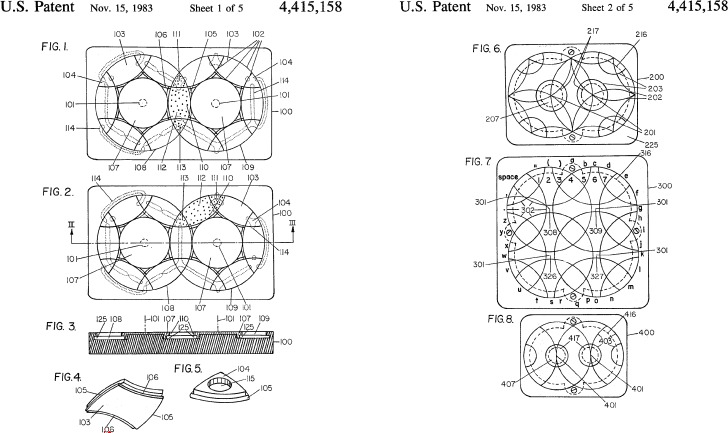
This patent by the author is the first to incorporate a method for coding and for including topological puzzles. It concentrates on overcut, symmetrical circle puzzles. Pieces are moved by sliding them This has the advantage of cheap manufacture and the disadvantage that the pieces and base must have a low coefficient of friction
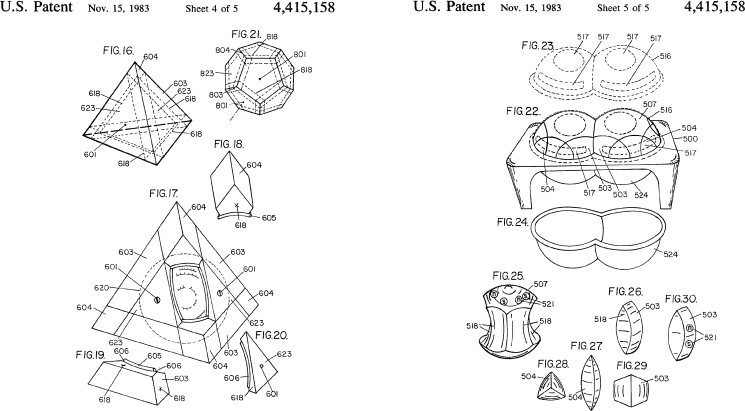
After the success of Rubik's cube everyone started thinking. Figures 16 and 17 are similar to Dr. Walter Moll's German patent. Figure 22 shows a completely new idea for an intersecting sphere puzzle
Solving a rotary puzzle can be difficult and frustrating. It is worse if you know nothing of the group theory (which consists of much arcane symbolism). One thing nice about rotary puzzles is their existence. Group theory has no preset form except that people agree about its symbolism. You could symbolize it in a million other ways. Rotary puzzles exist as pure spatial devices. This gives us a great means for illustrating the symbolic ideas of group theory. If you have a rotary puzzle you can observe permutations, cycles, and orbits in action. Learning is much easier when you have real world examples and applications.
All this will not help if you do not know group theory and have no desire to dip into it. The fact is that you have no choice but to learn some group theory if you hope to solve a rotary puzzle. The theory you devise and use may not look like standard group theory but you can bet that your theory has the identical kinds of ideas contained in it.
Here are some common sense ideas you can use to devise a solution of your own. Make a drawing of the puzzle and then make several photocopies of it. You will use these to record the result of some rotations. If you like notation better than drawings make a single drawing and letter the pieces and the rotary figures. The drawing is almost a necessity in devising a solution because you won't be able to easily memorize the necessary rotations, otherwise.
Your object is to discover moves that exchange or reorient some of the pieces while leaving every thing else in place. Usually it is better to begin the solution with one kind of piece and then the next kind until all pieces have been put in place. Each kind of piece will have an associated orbit. The orbit is all positions that can be occupied by that piece. You solve the puzzle by moving pieces in their orbits. Starting with one kind of piece you establish that its orbit must always be
taken first in your solution algorithm. Your finished algorithm can list the order of solution as an order of orbits O, R, B, ... and so forth.
Begin the solution with the simplest kinds of moves. A move known as a commutator is R, L, R-1, L-1. It says to rotate the rotary figure called R one notch clockwise. then rotate the rotary figure L one notch clockwise, then reverse by rotating R one notch anticlockwise, and then L one notch anticlockwise. After finishing this operation record what has happened to the pieces. The pieces that are left unchanged are not recorded so that you only have to show where moved and reoriented pieces have ended up. You can symbolize a number of rotations by a letter. The commutator above might be called C1. You may wish to know what happens, now, when you do C12 which means to do C1 twice. You might also try C1-1 which means to do C1 in reverse, C1-1 = L, R, L-1, R-1. Conjugations are powerful tools and you should try to explore several of these first.
Another useful technique Is to do a few mixing moves and then try to get the puzzle restored as nearly as possible but not quite completely restored. You have to record all moves precisely as you do this because one wrong notation will make the operation useless for future application. The mixing and restoring technique is probably the quickest way to find a solution to any rotary puzzle by using trial and error methods. The reason it works so well is that the restoring process puts most of the puzzle back in place so that you end up with only a few pieces in new positions.
In all the Rubik cube solution booklets I have looked at the solutions are very similar but all have differences. Rotary puzzles can be approached as problems in many different ways but understanding that solution is essentially very similar is a great leap towards solving even bigger puzzles.
If people could see forward and backward in time a few minutes puzzles like Rubik's cube might seem absolutely trivial and group theory might not even exist. This is because you would see many of the results of moves, and a glance at the puzzle would show you the path to a solution as well as thousands of mixing paths. You would be looking at a tree with puzzles as its leaves and you'd see it all at once so that the result of rotations is known as if all rotations were already performed. This far fetched view of rotary puzzles shows the necessity of using mathematics to solve them.
Bandelow, Christoph: Inside Rubik's Cube and Beyond Birkhauser, Boston, 1982
Berlekamp, E. R., Conway, J. H., and Guy, R. K.: Winning Ways for Your Mathematical Plays, Vol 2 Academic Press, New York, 1982
Eidswick, J. A.: Cubelike Puzzles--What are they and how do you solve them? American Mathematical Monthly, March 1986, 157-176
Frey, A. H., and Singmaster, D.: Handbook of Cubik math. Enslow Publishers, Hillside. NJ, 1982
Gardner, Martin: Mathematical Games Scientific American (Non-periodic tilings), January 1977
Golomb, Solomon W.: Rubik's cube and a model of quark confinement Amer J Phys , 49(11), November 1981
Hofstadter, Douglas R.: Metamagical Themas (The Magic Cube) Scientific American, March 1981
Hofstadter, Douglas R.: Metamagical Themas (Beyond Rubik's Cube) Scientific American, July 1982
Mandelbrot, Benoit B.: The Fractal geometry of Nature W H Freeman, NY, 1983, pp 46
Rowley, Chris: The group of the Hungarian Magic Cube, Algebraic Structures and Applications Proceedings of the First Western Australian conference on Algebra, 1982
Singmaster, David: Notes on Rubiks Magic Cube Enslow Publishers. Hillside, NJ, 1981
Wielandt, Helmut W.: Finite Permutation Groups Academic Press. New York, 1964
Wilson, Richard M.: Graph puzzles, homotopy and the alternating group J Combinatorial Theory Ser. B 16 (1974). 86-96
The text and original drawings are copyright © 1986, Douglas A. Engel, reproduced here with permission. Conversion to html and additional commentary by Jaap Scherphuis.