Rotascope

The Rotascope puzzle consists of three intersecting discs. As such it is similar to Trio, and the two-disc puzzles Turnstile and Rashkey. Unlike those puzzles however, the pieces are shaped so that they often prevent a disk from being moved. It can be considered a bandaged puzzle, closely related to the Bandaged cube, which was also invented by Raoul Raba. Raba named the puzzle Taquinoscope, but when it was manufactured by Pentangle it was given the name Rotascope. Below I reproduce the writing on the back of the packaging.

Object: To restore the original picture by rotating the 3 circles through 1/6th turns. Ensure that the circles are accurately aligned and do not use force.

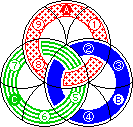
Hint: The ROTASCOPE is constructed from 13 curvilinear triangles (1 heart, 3 points and 9 shield-shaped pieces). The 'points' can never leave the circle they start in and the heart must be in the circle which you want to turn. Thus for example, if you start from figure one and rotate circle 'B' clockwise 1/6th turn, the only logical move that you can then make is to move circle 'A' 1/6th turn clockwise.

Another unique puzzle from the Pentangle collection

In 1873 Sam Lloyd invented the 15's Puzzle and started an international craze for the simple sliding squares puzzle. 109 years later these puzzles are still for sale in nearly every toyshop in the world.

In 1975 Erno Rubik invented the Magic Cube. Pentangle launched the puzzle on the unsuspecting Western world in 1979 seeding the craze of all time.

Pentangle is now proud to bring you the Rotascope which is a great puzzle combining the simplicity of Sam Lloyd's Fifteens puzzle with the complexity of Rubik's Cube. The Rotascope was invented and patented by Raoul Raba,

Pentangle, Wallop, Hampshire, England.
© Copyright 1977 Pentangle. Registered Design No. 1002813. Patents applied for.
Trespassers will be prosecuted.

(Algorithm & solution available from Pentangle if request accompanied by Certificate of insanity and Prescription Fee.)

Note that the name should actually be Samuel Loyd (not Lloyd), and that there seems to be no hard evidence of the 1873 date of the Fifteen puzzle. Raoul Henrique Raba first applied for a patent for the Rotascope on 10 October 1977 ( FR 2,405,077), well before the cube craze started. You can see images of this patent on Raoul Raba's homepage. His further patents to the Rotascope and some related puzzles are FR 2,463,632 (27-02-1981), FR 2,489,164 (05-03-1982), and FR 2,490,102 (19-03-1982).

The puzzle is two-sided. One side always shows a picture of three interlocking rings (Borromean rings, shown above), but the design of the other side varies. Mine has the Pentangle logo with a snake winding around it. The round black frame also has a small Pentangle logo, with 'Copyright 1980' on it.

If your browser supports JavaScript, then you can play Rotascope by clicking the link below:

JavaScript Rotascope

To see why this is a 'bandaged' puzzle, examine the two pictures below. On the left is the non-bandaged version, where every disc can always move 1/6th of a turn in either direction. On the right is the initial configuration of the Rotascope. Each piece has essentially been formed by fusing several pieces of the unbandaged puzzle.

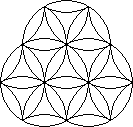
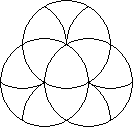
The puzzle is somewhat difficult because moves are very often blocked. Because of this, the possible positions do not mathematically form a group. Nearly all other moving piece puzzles do form groups because they are in effect (isomorphic to subgroups of) permutation groups, usually generated by the simplest possible moves. On this puzzle not every move is possible at every moment so the face turns cannot be considered generators of a group. See the Useful Mathematics page.

By computer search I examined how many configurations there are if we only look at the piece shapes, and ignore the printed pattern. It turns out there are 502 configurations, though only 49 have the 'heart' piece in the centre. The results are shown in the table below. It shows how many configurations there are for each number of disc turns from start versus number of 1/6th turns from start.

	Total	1	15	30	90	93	75	84	60	54	502
		Disc turns
1 / 6 t h t u r n s		0	1	2	3	4	5	6	7	8	Total
	0	1									1
	1		6								6
	2		6	12							18
	3		3	12	24						39
	4			6	36	36					78
	5				24	39	18				81
	6				6	18	30	30			84
	7						21	36	24		81
	8						6	18	24	18	66
	9								12	24	36
	10									12	12

The table shows that it takes at most 8 moves to get to the same configuration as the solved position (i.e. 'heart' in the centre, 'points' at outermost position of each disc). Once in this configuration only the nine 'shield' pieces need to be swapped about in order to solve it.

Once in a given configuration, the positions in such a configuration do form a (permutation) group. It is generated by the application of move sequences that return the puzzle to the same configuration. It turns out that only even permutations of the shield pieces can occur. The reason is quite subtle: Note that for a face to move, it must contain the heart piece. Any sequence of moves that permutes the pieces and brings them back to the same configuration must have an even number of 1/6th turns to bring the heart back to its original position. Therefore it must be an even permutation of the other pieces, and in particular an even permutation on the shield pieces. This exact same reasoning is used in the Bandaged cube.

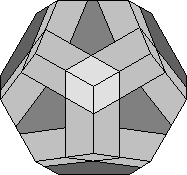
The reason it is so similar to the Bandaged cube is that the Rotascope is a kind of bandaged Megaminx as shown on the right. The number of configurations is not exactly the same because the megaminx has fivefold rotations, but if the Rotascope configurations that have a 'Point' piece in the centre are discounted, the two puzzles become identical.

I have calculated God's Algorithm for this puzzle. It turns out that it can be solved in at most 36 turns, or 44 moves if every sixth of a rotation counts as a move.

Click to view full table.

Disc Turns

Sixth Turns

Depth	Positions
0	1
1	15
2	30
3	90
4	150
5	240
6	474
7	720
8	1,188
9	2,040
10	3,876
11	6,180
12	10,488
13	18,144
14	30,528
15	50,724
16	88,278
17	154,662
18	254,955

Depth	Positions
19	431,283
20	725,976
21	1,205,944
22	1,964,436
23	3,219,099
24	5,089,053
25	7,596,524
26	10,664,865
27	13,466,636
28	14,528,616
29	12,865,414
30	9,310,276
31	5,576,836
32	2,739,474
33	907,929
34	158,244
35	9,396
36	96
Total	91,082,880
Avg Depth	27.272

Depth	Positions
0	1
1	6
2	18
3	39
4	90
5	144
6	240
7	348
8	540
9	756
10	1,284
11	2,052
12	3,648
13	5,268
14	8,568

Depth	Positions
15	12,888
16	21,552
17	30,888
18	51,642
19	80,220
20	138,063
21	196,794
22	320,208
23	480,951
24	797,773
25	1,110,342
26	1,774,176
27	2,588,271
28	4,105,250
29	5,234,799

Depth	Positions
30	7,450,476
31	9,144,411
32	11,597,986
33	10,841,508
34	10,843,992
35	9,235,770
36	7,355,596
37	4,276,521
38	2,093,400
39	733,383
40	390,117
41	114,531
42	38,328
43	30
44	12
Total	91,082,880
Avg Depth	32.272

Click to view summary table.

	Total	1	15	30	90	150	240	474	720	1,188	2,040	3,876	6,180	10,488	18,144	30,528	50,724	88,278	154,662	254,955	431,283	725,976	1,205,944	1,964,436	3,219,099	5,089,053	7,596,524	10,664,865	13,466,636	14,528,616	12,865,414	9,310,276	5,576,836	2,739,474	907,929	158,244	9,396	96	91,082,880
		Disc turns
S i x t h t u r n s		0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	Total
	0	1																																					1
	1		6																																				6
	2		6	12																																			18
	3		3	12	24																																		39
	4			6	36	48																																	90
	5				24	60	60																																144
	6				6	36	96	102																															240
	7					6	66	168	108																														348
	8						18	138	240	144																													540
	9							54	222	312	168																												756
	10							12	114	366	528	264																											1,284
	11								30	234	624	864	300																										2,052
	12								6	102	456	1,248	1,422	414																									3,648
	13									24	198	936	1,866	1,776	468																								5,268
	14									6	60	432	1,488	2,958	2,886	738																							8,568
	15										6	108	714	2,646	4,698	3,876	840																						12,888
	16											24	294	1,668	4,878	7,662	5,862	1,164																					21,552
	17												78	726	3,102	7,866	10,614	7,170	1,332																				30,888
	18												18	258	1,494	5,688	12,984	17,460	11,670	2,070																			51,642
	19													36	450	2,880	10,116	22,008	27,324	15,114	2,292																		80,220
	20													6	138	1,302	6,336	19,998	40,524	44,556	22,092	3,111																	138,063
	21														24	396	2,748	12,162	34,950	59,619	57,558	25,923	3,414																196,794
	22														6	114	1,014	5,790	22,332	57,282	95,430	92,190	40,836	5,214															320,208
	23															6	180	1,818	10,140	38,598	97,665	148,158	129,330	49,482	5,574														480,951
	24																30	594	4,560	23,022	79,500	174,219	243,514	196,398	68,823	7,113													797,773
	25																	96	1,404	10,032	45,798	135,171	267,630	330,192	237,261	75,774	6,984												1,110,342
	26																	18	396	3,810	21,738	84,408	231,588	429,912	516,576	363,864	112,116	9,750											1,774,176
	27																		30	708	6,570	38,274	148,902	388,284	683,082	744,948	454,065	114,906	8,502										2,588,271
	28																			144	2,154	17,322	87,522	298,116	714,238	1,141,386	1,112,676	593,478	130,075	8,139									4,105,250
	29																				396	5,466	36,846	162,828	510,705	1,087,419	1,511,520	1,256,562	559,974	98,451	4,632								5,234,799
	30																				90	1,608	13,614	74,760	296,592	834,756	1,647,732	2,137,398	1,645,926	682,206	111,438	4,356							7,450,476
	31																					114	2,250	21,192	120,150	468,303	1,286,325	2,348,382	2,617,704	1,665,333	539,712	72,408	2,538						9,144,411
	32																					12	450	6,606	49,316	245,400	867,818	2,108,895	3,276,580	3,044,856	1,545,755	404,137	46,631	1,530					11,597,986
	33																						36	1,164	12,918	87,096	401,292	1,254,729	2,579,103	3,201,390	2,255,112	861,873	172,095	14,424	276				10,841,508
	34																						12	282	3,648	28,992	157,968	604,602	1,623,396	2,858,178	3,025,026	1,841,754	612,648	84,792	2,682	12			10,843,992
	35																							6	204	3,366	29,436	171,873	687,990	1,774,224	2,679,453	2,312,526	1,199,868	339,012	36,990	822			9,235,770
	36																								12	612	7,764	54,516	268,821	877,608	1,740,815	2,051,208	1,488,710	690,600	162,246	12,486	198		7,355,596
	37																									18	672	7,620	51,903	236,625	686,115	1,144,062	1,140,228	735,102	245,100	28,416	648	12	4,276,521
	38																									6	156	2,130	16,122	76,578	243,486	476,514	587,604	468,768	191,040	30,150	822	24	2,093,400
	39																											18	438	3,882	25,044	99,342	215,472	241,062	125,925	21,654	534	12	733,383
	40																											6	102	1,140	8,562	39,840	99,648	128,439	84,636	25,614	2,118	12	390,117
	41																													6	258	1,992	9,672	28,503	43,674	27,018	3,384	24	114,531
	42																														6	264	1,722	7,242	15,360	12,054	1,668	12	38,328
	43																																			12	18		30
	44																																			6	6		12

Notation:

Hold the puzzle with the rings design at the front. The three 'point' pieces are marked A, B, and C. As these pieces can never leave the disc they started in, this also marks the three discs as A, B, and C. Hold the puzzle so that disc A is at the top. A clockwise 1/6th turn of a disc is denoted by the appropriate letter (A, B, or C) and an anti-clockwise turn by the letter with an apostrophe (i.e. A', B' or C'). The shield pieces are marked 1-9, so I will use the same numbering in the solution.

Solution:

Phase 1: Bring the puzzle into the right configuration

Use any move to bring the heart to the centre. Its orientation need not be correct.
Now the three 'point' pieces need to be brought to their correct positions at the outermost edges of each disc. This can be done by using the sequences C'A', B'C', A'B' and their inverses A C, C B and B A. Note that each of these sequences turns two discs in the same direction and leaves the heart piece in the centre. First move any point pieces that are adjacent to the heart piece in the centre. Once no point pieces are next to the centre, at most two more of the sequences are needed to put them in position.

The rest of this solution is mostly just a list of move sequences, one sequence for each possible way each piece needs to move. I found these sequences by a computer search, and while there are too many for the solution to be really suitable for memorisation, it is relatively fast.

Phase 2: Solve piece 8.

Find piece number 8, and figure out which piece would normally be in that position.
Depending on where piece 8 is, do one of the following:
1. AC B'C' A'B' CB C'A' BA
2. B'C' BA CB A'B'
3. CB C'A' B'C' A'B' AC BA
4. A'B' AC BA CB C'A' B'C'
5. AC A'B' C'A' BA
6. B'C' BA C'A' CB AC A'B'
7. A'B' AC BA C'A'
9. CB C'A' B'C' AC

Phase 3: Solve piece 9.

Find piece number 9, and figure out which piece would normally be in that position.
Depending on where piece 9 is, do one of the following:
1. A'B' AC BA CB C'A' A'B' B'C' BA
2. B'C' C'A' CB BA B'C' AC A'B' CB
3. B'C' C'A' CB AC B'C' C'A' CB AC
4. BA AC A'B' C'A' C'A' B'C' AC CB
5. B'C' BA C'A' CB A'B' B'C' AC CB
6. C'A' B'C' AC CB C'A' B'C' AC CB
7. AC B'C' C'A' CB A'B' CB BA B'C'

Phase 4: Solve piece 1.

Find piece number 1, and figure out which piece would normally be in that position.
Depending on where piece 1 is, do one of the following:
2. BA AC A'B' B'C' BA C'A' CB A'B'
3. B'C' AC CB C'A' BA CB A'B' B'C'
4. BA B'C' AC A'B' CB BA C'A' A'B'
5. AC BA C'A' A'B' AC BA C'A' A'B'
6. AC B'C' C'A' BA AC A'B' CB C'A'
7. BA AC A'B' C'A' BA AC A'B' C'A'

Phase 5: Solve piece 2.

Find piece number 2, and figure out which piece would normally be in that position.
Depending on where piece 2 is, do one of the following:
3. CB AC B'C' B'C' C'A' CB AC CB C'A' B'C'
4. AC A'B' C'A' CB BA C'A' B'C' B'C' AC CB
5. CB A'B' B'C' BA C'A' A'B' AC CB BA B'C'
6. CB A'B' B'C' C'A' BA AC A'B' CB BA B'C'
7. A'B' CB BA B'C' BA C'A' A'B' B'C' AC CB

Phase 6: Solve piece 3.

Find piece number 3, and figure out which piece would normally be in that position.
Depending on where piece 3 is, do one of the following:
4. B'C' BA CB C'A' A'B' AC BA B'C' A'B' AC CB C'A'
5. AC B'C' C'A' BA CB A'B' C'A' BA AC B'C' A'B' CB
6. B'C' BA CB CB A'B' B'C' A'B' AC BA B'C' C'A' CB
7. B'C' AC CB A'B' C'A' BA CB BA B'C' B'C' A'B' CB

Phase 7: Solve piece 4.

Find piece number 4, and figure out which piece would normally be in that position.
Depending on where piece 4 is, do one of the following:
5. B'C' BA CB A'B' CB AC B'C' C'A' BA C'A' A'B' AC
6. B'C' AC CB A'B' C'A' CB BA BA B'C' C'A' A'B' B'C' AC CB
7. B'C' C'A' CB BA AC CB A'B' A'B' B'C' AC BA B'C' C'A' CB

Phase 8: Solve piece 5.

Find piece number 5, and figure out which piece would normally be in that position.
Depending on where piece 5 is, do one of the following:
6. AC B'C' A'B' CB BA C'A' B'C' AC BA C'A' A'B' CB
7. B'C' BA AC A'B' C'A' CB AC A'B' B'C' BA CB C'A'
Pieces 6 and 7 should fall into place automatically.

Jaap's Puzzle Page

Rotascope

Another unique puzzle from the Pentangle collection

JavaScript Rotascope

The number of positions:

Links to other useful pages:

Notation:

Solution: