CUBIC CIRCULAR
A quarterly newsletter for Rubik Cube addicts
Issue 3 & 4 Spring & Summer 1982
| CONTENTS | | | |
| Editor's Corner | | 2 | |
| Songs | | 2 | |
| Answer | | 2 | |
| Cubic Quarterlies | | 3 | |
| The First World Championship | | 4 | |
| Cubic Cannabis | | 7 | |
| New Cube Products | | 8 | |
| A. Pryl - Fool! | | 13 | |
| Rubik's Revenge - The 43 | | 14 | |
| Winning Ways on the U Group | | 17 | |
| The 53 | | 18 | |
| The Magic Dodecahedron and Alexander's Star | | 19 | |
| Magic Polyhedra | | 21 | |
| Rubik Robots | | 25 | |
| Pretty Patterns | | 26 | |
| Orders of Elements | | 34 | |
| The Magic Disc | | 36 | |
| Comments on the U Group | | 36 | |
Published by David Singmaster Ltd., London, England. ISSN NO 0261-8362
2
EDITOR'S CORNER
When I started the Cubic Circular last year, I. intended to have 12 pages per issue and
I wondered how I would fill them. As it turns out, material continues to arrive faster
than I can deal with it or publish it, and two other magazines have started. The first
two Circulars were already 16 pages and I have about 40 pages of type-script in front of
me. Because of this and because the Spring issue is a bit late, we have decided to make
this a DOUBLE ISSUE for Spring and Summer, i.e. issues number 3 & 4. Depending on how
the material fits and on the printer, this issue will be 32 or 36 pages.
Hence this issue completes the first year of the Circular. The next issue will appear
in the Autumn, probably in October or November. Because of the extra weight of larger
issues, the need to employ technical assistance and the fact that circulation is still
confined to a small circle of cubologists, we find the current subscription of £2.50 per
year is not really covering our costs. Hence we must raise the subscription to £4.00
for the next year (or $8.00). This may be revised later but we will accept renewals now at
this rate.
Do it faster!
SONGS
Mister Rubik, by the Barron Knights, (C1-15)
is now on their LP "Twisting the
knights Away". An English school group did a song of their own on TV while trying
to restore their cubes at the same time. They didn't finish.
A Hungarian husband and wife, Bea Muszty and András Dobay, have made an English
single called "Trick in the Middle" about Rubik's cube (Start Records SP5 70537) -
"Try to harmonize the colours of your life
Or the faces of the cube to be alike.
You can twist, twiddle and fiddle,
But the trick's in the middle of the cube."
Don Taylor has sent a photocopy of the cover of the Australian song. It's called
"The Cube" by Mike Brady and the Cubettes. It has been done as a video clip with
dancers.
Claude Shannon has composed "A Rubric on Rubik Cubics" to the tune of 'Ta! Ra!
Ra! Boom De Ay!'. It has six verses of 8 lines with six 4 line choruses, and ten footnotes:
It's a bit long to copy here, but perhaps I'll put it in a later Circular.
ANSWER
The answer to the film question on C2-4 is that the film was run backwards!
3
CUBIC QUARTERLIES
The first issue of Rubik's Logic and Fantasy in Space has appeared (C2-3). It appears in
several languages simultaneously. The price is now listed at $2.00 per issue. The contents
are as follows: (Some of the information will be excerpted elsewhere.)
Introduction by Rubik
The Order of Disorder. This is an essay on entropy and the Cube.
Mr. Cube - Ernő Rubik - a sketch. This is an interview with Rubik, one of the best
and most informative that I have seen.
Mister Rubik. Words of the song and a story about the Barron Knights (C1-15).
A world you can twist around, by Gerzson Keri. An essay on patterns - achievable,
constructible and even unconstructible ones!
Letters to the editor.
From five thousand to fifteen millions. A report on Politechnika's production of the cube.
Student Olympics. A report on the International Mathematical Olympiad.
Geometrical Art - The Magic of Shapes. An essay on cubism and on cube images in art.
Cube Fans - Competitions and clubs ; Our London correspondent reports
Puzzles page
Around the World - press cuttings.
Reviews of "You can do the Cube" and of my Notes.
Toy-Business; Varikon. An article on Konsumex products, especially the Varikon barrel
puzzles.
The Computer, my playmate. An essay on computer games.
Corner - a page of cartoons.
The first issue of Rubik's Cube Newsletter (from PO Box 72, Hollis, New York, 11423,
USA for $5.00) appeared in May and has just arrived. It's 8 sides, printed on a single
piece of paper and folded, in red and black. The contents are:
At the US National Championships
The Editor's Cubie
Upcoming Cube Clinics
Sneak Preview: 2 new Rubik's Puzzles
Cube Contest Kits
Cube Club Calendar
Membership Offer
Letters to the Editor
Local Clubs
Final Standings & Times
1981 Regional Cube-A-Thon Records and Results
The membership offer includes several new spinoffs: 'Keep on Cubin' tee shirts and
badges, pencils, patches, a mobile!, neck ties and memo pads!
4
THE FIRST WORLD CHAMPIONSHIP
The first Rubik's Cube World Championship was held in Budapest on 5 June 1982. This was
jointly sponsored by Politoys, Konsumex and Ideal. There were contestants from 19 countries.
Minh Thai, the US champion, won with a time of 22.95 sec.
The competition was efficiently organized by Brian Cartmell, the public relations firm
for Ideal (UK), so it had the same basic structure as the UK contest. The cubes were
selected by Rubik from a special production run and competitors were given a sample to
practice with. Competitors described them as pretty good. All had a standardized colour
pattern with white opposite yellow, red opposite orange and blue opposite green (David
Sibley calls this the 'plus and minus yellow pattern' since opposite faces differ by
yellow.) and with blue, orange, yellow clockwise at a corner (spelling BOY). Rubik worked
with some mathematicians to develop several patterns of similar complexity. (The
contestants remarked that all the patterns seemed of equal difficulty.) Four sets of cubes
were put in four of these patterns by Rubik and sealed in separate briefcases which were
kept in a bank overnight and brought to the competition by the supervising lawyer. One case
was opened and placed by the competitor's entrance. Each contestant picked one at random as
he came on stage. (The competitors remained offstage until their turn came so they could
not watch the previous attempts.) Each contestant had three attempts and the best time was
taken. The fourth cube was used as an extra cube in case a cube came apart. In this event,
the contestant got one extra trial. This happened seven times. The Finnish contestant's
cube broke twice, so he lost one trial.
The contestant had fifteen seconds to examine the cube in his hand. It was then set down
on a photoelectric base. The timing was then based on the time from picking up the cube to
setting it down again in completed form.
There was a jury consisting of Rubik, myself, Georgina Tamás (Commercial Director,
Konsumex), Peter Peacock (Marketing Director, Ideal (UK)), Rainer Seitz (Product Manager of
Arxon and founder of the Rubik's Cube Club). Basically the jury was to guarantee fairness
in the event of unexpected phenomena. Indeed the power for the TV and the display timer gave
out in the middle of one trial. Fortunately the timing computers are battery powered and a
valid time was obtained. One contestant started to do the cube during the study time - he
was given an extra try. Once the display timer wouldn't reset after the study time and there
was some delay, so the contestant was allowed a new examination period.
The order in the first round was determined by a drawing the previous night. On the
following rounds, the slowest contestants went first. The logo of the contest was a cube
with one corner replaced by a globe. The prizes were three examples of these which were
plated in gold, silver and bronze, together with a number of elegant Hungarian handicrafts.
5
The Contestants
I give a summary about each contestant: Country. Name, age, home city, occupation,
personal best time, winning time in national championship (labelled: won in ...). Comments.
Austria. Josef Trajber, 25, Vienna, computer programmer, 29 sec. Author of two
books on the Cube. Inventor of an octahedron (C1-7/8)
Belgium. Luc van Laethem, 25, Kraainem (near Brussels), student, 17 sec. Did 100
Cubes in 54 minutes (32.4 sec average).
Bulgaria. Svilen Tenev, 18, Plovdiv, student of languages, 40 sec.
Canada. Duc Trinh, 14, Kitchener (Ontario), student, won in 26 sec. Originates
from Viet Nam.
Czechoslovakia. Jiri Fridrich, 17, Ostrava-Poruba, student, won in 23.55 sec.
Finland. Jan Sandqvist, 21, Helsinki, advertising representative, 19 sec.
France. Jerome Jean-Charles, 26, Paris?, journalist, won in 25.60 sec.
Great Britain. Julian Chilvers, 15, Eaton (near Norwich), student, won British
Isles Championship in 25.79 sec. He has done 44 cubes in 20 minutes (27.3 sec average!).
Holland. Guus Razoux Schultz, 17, ?, student, 18.50 sec.
Hungary. Zoltán Lábas, 26, Nyiregyhaza (near Budapest), student,
34.5 sec, won in 36.9 sec average.
Italy. Guiseppe Romeo, 16, Rome, student, won in 26 sec.
Japan. Ken'ichi Ueno, 18, Tomakomai (near Sapporo City), student, 22 sec, won in
42.30 sec.
Peru. Eduardo Valdiva Chacón, 21, Lima, student, 26.80 sec.
Poland. Piotr Serbenski, 17, Warsaw, student, 28.50 sec.
Portugal. Manuel Moura Galrinho, 24, Setubal, professor of philosophy, 25.80 sec.
Sweden. Lars Petrus, 21, Uppsala, student of technical physics at Uppsala
University, won in 24 sec.
United States. Minh Thai, 16, Los Angeles, student, won in 26.06 sec. Seven days
after buying a Cube in June 1981, he could do it in under two minutes. Came to US 3 years
ago from Viet Nam, speaking no English.
6
West Germany. Ronald Brinkmann, 17, Hamburg, student, won in 19 sec.
Yugoslavia. József Borsos, ?, ?, student, won in 28 sec.
The average age was about 20 years, which was older than I expected. Jean-Charles and Lábas were the oldest.
Results
Best times are underlined. B indicates breakage resulting in one extra trial.
| Round | Best | | Ave. |
| Name (country) | 1 | 2 | 3 | time | Rank | time |
| Borsos (Yug) | 36.75 | 35.33 | 30.02 | 30.02 | 13 | 34.03 |
| Brinkmann (BDR) | 34.80 | 30.59 | 32.32B | 30.59 | 14 | 32.57 |
| Chacón (Per) | 34.91 | 29.62 | 30.01 | 29.62 | 11 | 31.51 |
| Chilvers (GB) | 30.59 | 25.95 | 27.46 | 25.95 | 7 | 28.00 |
| Fridrich (Cze) | 31.49 | 29.11 | 33.20 | 29.11 | 10 | 31.27 |
| Galrinho (Por) | 40.74 | 48.67 | 37.11B | 37.11 | 16 | 42.17 |
| Jean-Charles (Fra) | 27.87 | 31.18 | 25.06 | 25.06 | 6 | 28.04 |
| Lábas (Hun) | 24.49 | 27.58 | 28.21B | 24.49 | 3 | 26.76 |
| van Laethem (Bel) | 32.92 | 34.98 | 29.73 | 29.73 | 12 | 32.54 |
| Petrus (Swe) | 35.42 | 33.11 | 24.57 | 24.57 | 4 | 31.03 |
| Razoux Schultz (Hol) | 24.32 | 31.51 | 26.15 | 24.32 | 2 | 27.33 |
| Romeo (Ita) | 34.23* | 41.75 | 28.11 | 28.11 | 9 | 34.70 |
| Sandqvist (Fin) | 31.17B | B | 31.56 | 31.17 | 15 | 31.37 |
| Serbenski (Pol) | 44.40 | 37.50 | 40.86 | 37.50 | 17 | 40.92 |
| Tenev (Bul) | 51.88 | 47.29 | 47.35 | 47.29 | 18 | 48.84 |
| Thai (USA) | 27.16B | 22.95 | 27.97 | 22.95 | 1 | 26.03 |
| Trajber (Aus) | 50.16 | 54.93B | 58.99 | 50.16 | 19 | 54.69 |
| Trinh (Can) | 37.44 | 26.63 | 36.09 | 26.63 | 8 | 33.39 |
| Ueno (Jap) | 27.56 | 27.90 | 24.91 | 24.91 | 5 | 26.79 |
* Romeo's first cube broke three times but he reinserted the piece each time and carried
on. Had he stopped, he would have been given an extra trial.
I have computed the average time for each contestant out of curiosity. The averages do
not give results greatly different than the best time. Thai would have won on average as
well as best time!
Championship Techniques
I asked all the contestants what algorithm they used. Borsos' algorithm was unclear to
me. Brinkmann and Chilvers had two possible algorithms. The following descriptions assume
doing the D face first, but this doesn't mean they hold it that way. I write DC for D
corners, ME for middle edges, etc. The most popular method was to do DC, UC, U & D E,
ME (C2-3). This was used by Brinkmann, Chacón, Chilvers, Jean-Charles, Labas,
Sandqvist, Thai, Trinh, van Laethem. Ueno did DC, UC, ME, 3UE, rest.
7
The second most popular technique was Pierre Jullien's method of leaving a DC and the
ME above it undone as working or parking spaces. Galrinho, Romeo and Tenev used this
method. Brinkmann used a method DC, 3DE, 4UC, rest. Variants of the D, M, U layer method
were used by Fridrich, Serbenski and Trajber. Chilvers did DC, DE, U, M. Razoux Schultz
did DE, DC & ME together, U (see N32). Petrus does a 2 × 2 × 3 block then orients edges,
then orients corners, then completes D & M and then U. (See N32-33.) He gets a 57 move
average.
OTHER COMPETITIONS
The Hungarian Championship was held on 27 September 1981. A local elimination round gave
300 competitors and a second round on 20 September left 128, classified as under 15, 15 to
18, over 18, containing 58, 31 and 39 competitors. Three trials were made and the average
time taken. The best five in each class then formed a three trials, average time, final.
Zoltán Lábas won the over 18 class with an average of 37.1 sec and the final
with 36.9 sec.
The Czech competition, held on 11 May, had three categories: children up to 10 years;
women and girls; men and boys. In the semifinals they had seven trials and the middle five
were averaged, but the finals were for best time out of three trials. Jiri Fridrich, 17, of
Ostrava-Poruba, was first in the semifinals with an average of 32.24 seconds and in the
finals with a best time of 23.55 seconds.
There have been a number of charity cube contests in the UK. These try to do as many
cubes as possible in a given time, often 10 or 20 minutes. Dame Kathleen Ollerenshaw
organized one in Manchester for the St. John Ambulance on 6 March. Mal Davies organized
one in Birmingham for the English Schools Athletics Association on 15 May. At the first,
Anthony Willetts did 29 cubes in 20 minutes. At the second, John Duffy and Anthony Willetts
did 33 cubes in 20 minutes (36.4 sec average). I saw John White do a cube completely behind
his back (136 sec). Richard Hodson improved his one-handed time to 77.50 sec., but Duncan
Dicks, a 2nd year student at Warwick University, did 59.32 and 53.29 sec. Hendon School
(outer London) had a contest for the Barnet Mayor's Appeal for research into Crohn's
Disease.
Two London policemen, Tim Timoney and Barry Pullen, held a 24 hour cube marathon
at Keddies in Romford to raise money for a five year old girl suffering from an inoperable
brain tumour. They restored 1000 cubes in 22 hours 25 minutes and acquired severe cases of
Cubist's Thumb. They raised over £2000 to send the girl and her mother to Lourdes and
Disney World.
CUBIC CANNABIS
Rubik Cubes were banned at Wandsworth Prison, London, after one was found to be stuffed
with cannabis!
8
NEW CUBE PRODUCTS
In C2, I discussed a number of new sliding block puzzles. Here I will discuss new cube
type puzzles. Several of these are discussed elsewhere.
Ideal is bringing out a 'Rubik's Range' of cube products, apparently all selected and
supervised by Rubik and some of which originated with Rubik. The 43 is part of
this range. There is also a 23 with Ishige's mechanism called Rubik's Pocket
Cube, and a 33 globe with a rather schematic map called Rubik's World. The
Calendar Cube (C1-5) is also in the Range. This was devised
by Marvin Silbermintz of Ideal in New York, and strikes me as one of the neatest
variations. Because Wednesday is Mittwoch, it is possible to set two days at once on the
German version. (Exercise: find all such pairs. This depends on the year!)
Rubik's Challenge is a 33 with holes for pegs in the facelets. Each player
chooses a colour, puts a peg in a facelet of that colour and then gives a turn. The object
to get three of your pegs in a row.
Rubik's Race is a 5 × 5 board with four pieces of 6 colours in it. A container of nine
tiny cubes is shaken to produce a 3 × 3 pattern. The race is to slide the pieces on the
board so as to get the 3 × 3 pattern in the middle.
Ideal is also bringing out the Popeye 23 (C1-6), made by Tsukuda (Japan) and
Alexander's Star.
Konsumex, the Hungarian trading company which exports the Cube, has a number of other
cube products produced by Politoys. Rubik's Mini Cube is a small 23 with only
three colours and a mechanism which is a bit like Ishige's, but without an inner sphere.
See below for schematic cross sections of both mechanisms. In both cases one corner is fixed
to the centre.
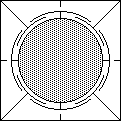 |
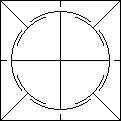 |
| Ishige's Mechanism |
Rubik's Mini cube |
9
There are several Taiwanese 23's with a different mechanism. I haven't taken
one apart yet.
They come with two types of die pattern as well as Popeye and ordinary
patterns. The Mini Cube has three pairs of adjacent faces with identical colours. It turns
out that this allows two colour patterns, one of which is impossible to achieve!
The Magic Domino has been re-engineered and now has a much smoother action. It is also
being made in a version with raised spots for the blind.
General Impex is the other Hungarian trading company which exports the Babylon Tower
(C2-12), the Hungarian Rings (C2-14) and the Magic Dodecahedron. They displayed a
23 Magic Globe attributed to a Mr. Csillam.
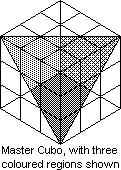 Mondadori, the Italian distributor of the cube, is doing two variants. The Fifteen Cubo
is a Magic Square Magic Cube with black numbers on gold labels. (See C1-5.) The Master Cubo
has 12 colours which essentially colour the edges. Here the centre orientations are
important but the edge orientations are not and there are
8!·38·12!·46/2·2·3 patterns,
which is the same as on the ordinary cube!
Mondadori, the Italian distributor of the cube, is doing two variants. The Fifteen Cubo
is a Magic Square Magic Cube with black numbers on gold labels. (See C1-5.) The Master Cubo
has 12 colours which essentially colour the edges. Here the centre orientations are
important but the edge orientations are not and there are
8!·38·12!·46/2·2·3 patterns,
which is the same as on the ordinary cube!
Toni Obermaier, of the German sports equipment firm Togu, has applied for patents on
a 23, a 43 and a 53. He has started production of a series
of eight 23 with different colour patterns. The simplest has only two colours
with four solidly coloured cubelets of each colour. Though advertised as having 70 patterns,
there are just 7 when symmetries of the cube are considered. Any two patterns are at most two moves apart!
Obermaier describes this as suitable for preschoolers. Enumerating the
patterns, considering the symmetries, is quite a tricky task for the different colour
patterns. The mechanism is like Ishige's.
When I was in New York over Christmas, I found examples of cubes with flags, die
patterns, animals and nudes (not to be confused with the other Boob Cube which only turns
on one axis).
10
Ole Jacobsen sends an example of an idea of Jim Saxe and Dan Hoey. There are 6 cyclic
arrangements of four colours. Take a blank cube and put four coloured spots in the corners
of each facelet, so the 6 arrangements are each on one face. I find this cube makes you
colour blind! A Korean variation of the cube uses thin (about 1 mm) plastic covers on the
facelets rather than the PVC stickers. I saw these in the US being sold as the Deluxe
Version of Rubik's Cube at $15.00.
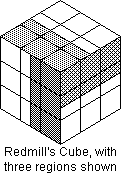 Another variant is the Banana Puzzler which has six colours of bananas on white labels
and the box says "This puzzler will drive you bananas". Peter Redmill sends a
different type of edge colouring. He has each face split in half. The halves can be viewed
as corresponding to edges. There is a way to colour the edges with four colours so the
three colours of each edge are along three orthogonal intersecting edges, as shown.
Another variant is the Banana Puzzler which has six colours of bananas on white labels
and the box says "This puzzler will drive you bananas". Peter Redmill sends a
different type of edge colouring. He has each face split in half. The halves can be viewed
as corresponding to edges. There is a way to colour the edges with four colours so the
three colours of each edge are along three orthogonal intersecting edges, as shown.
John White, of Warwick University, has invented a non-trivial Irish Cube
(C1-5). It has
two colours arranged as shown. He has made a large number of other colour patterns.
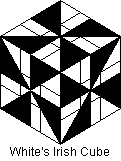 Henry and Bruce Dan, of Atlanta, Georgia, have been making solid colour cubes by buying
lots of ordinary cubes and peeling the labels. (They could have bought white or black cubes
directly from Ideal!) The Taiwanese have sold a black cube as The Executive Polish Cube.
"Its total lack of reason for being will keep you fascinated for several minutes, or,
perhaps, only a few seconds ... try to solve the puzzle with your eyes closed ... work the
puzzle in the dark."
Henry and Bruce Dan, of Atlanta, Georgia, have been making solid colour cubes by buying
lots of ordinary cubes and peeling the labels. (They could have bought white or black cubes
directly from Ideal!) The Taiwanese have sold a black cube as The Executive Polish Cube.
"Its total lack of reason for being will keep you fascinated for several minutes, or,
perhaps, only a few seconds ... try to solve the puzzle with your eyes closed ... work the
puzzle in the dark."
11
In New York, I found the small rhombi-cubo-octahedron (C1-9) with three colours instead
of ten. Recently I have seen the shape obtained by intersecting three octagonal prisms at
right angles. This is a bit like the small rhombi-cube-octahedron, but the corner pieces
are pyramids rather than being flat. I haven't yet discovered the name of this shape. It
has twelve colours corresponding to the edges.
.
Trajber's Octahedron (C1-7/8) has been produced in Taiwan,
in two forms. The other form has the vertex pieces slightly truncated. Tsukuda (Japan)
advertise a 2 cube-octahedron.
The range of cube related products is also amazing. Perhaps most intriguing are cube
earrings! These are about 12.5 mm (1/2") on a side. One version doesn't turn at all.
Another turns on one axis only. In New York, I saw hair slides (or barrettes) and a cube
jig-saw puzzle.
.
In the UK are mugs ("It's a Mug's Game"!), a memo cube and a
poster version of the solution. At least a dozen cubic tee-shirts are available, mostly
in the US. Kit-Kat and Olympic Holidays used the Cube in bill-beard advertising. Hamlet
Cigars has a Cube being restored, but it turns out to have a blue centre in the white
face, so the user throws it away and lights up a cigar. The cube rotation is by me.
I have seen a number of chimerical cubes (C1-9). The simplest are obtained by taking
one, two or three columns from an octagonal prism and putting them into an ordinary cube.
See below for an example. Actually, I have just realised that one need net make them
parallel and a rather odd shape is obtained with three orthogonal nonintersecting columns,
as shown below.
12
Tony Fisher, of Ipswich, has made what I call Siamese Cubes. Take two ordinary cubes
each with one column replaced by a column from an octagonal prism. Glue the cubes together
along these columns. The pieces do not move from one cube to the other, so each cube
behaves like an ordinary cube with one column glued together. Exercise: Consider any
pattern on the cube, which has a column correctly lined up. Prove or disprove that the
cube can be restored without breaking up the column.
.
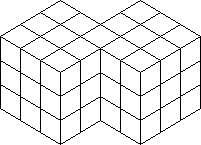 |
| Fisher's Siamese Cubes |
One could join two Cubes at a corner, using a piece from a truncated Cube, or crossways
at an edge: I can't see any way to join two Cubes which allows mixing pieces.
Another chimera from Taiwan is a mixture of corners from a truncated Cube and edges from
a cubo-octahedron.
Uwe Mèffert came to the London Toy Fair with about 30 new products, several of
which will be appearing soon. The Magic Dodecahedron is mentioned elsewhere. The Pyraminx
Star is a stellated and sparkly version of the Pyraminx. It is even easier to solve, but
it makes a most handsome object.
The most interesting of Mèffert's products is the Pyraminx Cube, invented by
Tony Durham, an English journalist. It is a cube which is bisected by the four planes
through the centre and perpendicular to the diagonals. It rotates on each of the planes,
a movement which people have difficulty in discovering. There are 6 faces and 8 corners.
There is a dual structure which is an octahedron with 8 faces and 6 edges. I find
4!·4!·6!·38/2·2·24 = 283 43520 patterns
for the cube and
4!·4!·6!·26/2·2·2·4! = 1 38240 patterns
for the octahedral version. (We get 26 rather than 46 for the reasons
explained under Magic Polyhedra.) The octahedral version was invented earlier by Rubik.
13
 |
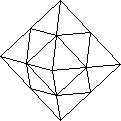 |
| Pyraminx Cube |
Magic Octahedron |
It is possible to make both the 6 four-sided pieces and the 8 three-sided pieces have
recognizable orientation either by various colourings or by embedding the four axes into
a less symmetric solid - Durham uses a dodecahedral shape. I get
4!·4!·6!·38·26/2·2·2·24
= 9069 92640 patterns in this case. However, I have just read over Durham's work on the
number of patterns and he finds two further conservation rules which are quite interesting.
I haven't had time to fully assimilate them, but they give two twist conservation laws for
the cube and dodecahedron cases, yielding 1/9 of the results I have just given, namely,
31 49280 and 1007 76960. I will return to this one once the objects become available - no
point in spoiling your fun completely.
A. PRYL - FOOL!
The Prague newspaper, Mlada Fronta, ran a story on 1 April about a school giving courses
on the cube. The school's director was A. Pryl whose best time for the cube was 69 hours,
37 minutes, 58 seconds. The teachers were Frantisek Kubík, age 12, and Miloslav
Kostečka, age 9. The Associated Press picked up the story and The International Herald
Tribune (IHT) ran it, but they lost some of the points by christening A. Pryl as Antonin
Pryl and omitting his time. When I read the IHT report it seemed quite genuine. Mlada
Fronta ran the IHT article in English with Czech commentary, "Believe or Not Believe
- We Have Caught a Whale". Mojmír Sob, who has kindly sent the details of this
epic, points out that Pryl, Kubík and Kostecka are common Czech names, though the
last two are also Czech words for a small cube.
14
RUBIK'S REVENGE - THE 43
The 43 is appearing. I have received an early sample via Rainer Seitz and it
works pretty well. Ideal is advertising it as Rubik's Revenge in the US and UK and as
Rubik's Master Cube in Germany, but has only made a few deliveries so far in the UK. It is
66 mm (about 2 5/8 ") on an edge and weighs about 240 gm (about 8 1/2 oz) which makes
it about one-third denser than the ordinary cube (57 mm edge, weighing 120 gm).
The mechanism is basically a grooved sphere, but there are several points where it varies
from designs I have seen. The centres are the only pieces hooked on to the sphere. The four
centres of a face turn in a circular opening where two grooves meet. There is only one
central groove in each direction for the slices to turn along, but these grooves are
asymmetric so that one slice will turn with respect to the sphere, but the parallel slice
carries the sphere with it. No piece is attached to the central sphere. The 43
will come apart in much the same way as the 33, but one must remove all the edges
and corners of a face and spread out the centre pieces in order to disengage a centre piece.
I don't know the source of this mechanism.
Three books on the 43 are about to appear from Minh Thai, Jerome Jean Charles
and Tom Werneck. All of these have been written without a 43 in hand!
I received my 43 in Budapest and began to work on it on Saturday evening.
Thinking that the methods of the 33 would solve the edges and corners, I put
the centres right first. This is not too difficult. I then got the edge pieces in pairs,
but stopped when I needed a single 3-cycle of edges. The next morning, while flying back
to London, I saw how to do this and then put the edges and corners correct. However, I made
a boo-boo later and then tried the same method and discovered I needed a single 2-cycle of
edges! After applying a 3-cycle I wanted a 4-cycle and I had to leave it like this. I
returned to it a few days later and saw how to form a 4-cycle, but this moved centres.
Finally, I saw an easy method to 3-cycle centres only. So, my strategy is to get the edges
correct first, then centres and corners, which are easily done, but everything takes some
time. A layer by layer method is feasible, but the edges of the last layer will need some
tricks. If the last layer is a face, it will be very awkward to get a 2-cycle of edges.
Hence it may be best to do two opposite faces and then the slices between them.
Number of patterns
The number of patterns on the 43 has been considered by Herb Taylor, Solomon
Golomb and David Kantor in Los Angeles.
15
Taylor and I have located an error in the argument at C2-8. The factor of 24 in the
denominator arises since the 6 sets of 4 identical centres can be permuted in 24 ways each
and the cube has 24 indistinguishable orientations. However since the parity of centre
turns is the same as the parity of corner turns, only half of the 24 cases are possible.
This is the same reasoning that gave the 2 in the denominator at C2-6 and was used several
times on C2-9/12. Thus the correct (I hope!) answer is
8!·24!·24!·38/(3·247) =
7 40119 68415 64901 86987 40939 74498 57433 60000 00000
= 7.4 × 1045
Notation
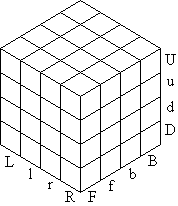 Kurt Endl has proposed a notation using A, B, C, D, 1, 2, 3, 4; I, II, III, IV to
represent the levels in a 43. This has the advantage of being indefinitely
expandable, but I prefer a notation which retains some mnemonic character like the B, L, U,
D, F, B notation for the 43 . I find the following seems to be the most
convenient for me. Label the 'slice' layer adjacent to each face by the lover case letter
of that face. Thus the four levels from left to right are denoted L, l, r, R as shown in
the diagram. Similarly we use U, u, d, D and F, f, b, B. Because we do not have centre
pieces, one must be careful physically to remember which directions are which, or one can
keep a corner fixed, as with the 23 (N53).
Kurt Endl has proposed a notation using A, B, C, D, 1, 2, 3, 4; I, II, III, IV to
represent the levels in a 43. This has the advantage of being indefinitely
expandable, but I prefer a notation which retains some mnemonic character like the B, L, U,
D, F, B notation for the 43 . I find the following seems to be the most
convenient for me. Label the 'slice' layer adjacent to each face by the lover case letter
of that face. Thus the four levels from left to right are denoted L, l, r, R as shown in
the diagram. Similarly we use U, u, d, D and F, f, b, B. Because we do not have centre
pieces, one must be careful physically to remember which directions are which, or one can
keep a corner fixed, as with the 23 (N53).
It is clear how the notation records moves, but we must adapt it a bit to label pieces
and positions. We now have two FU edges and four F centres. So we shall now label each piece
with three symbols, corresponding to the three levels it lies in. Each edge lies in two
faces and a slice and each centre lies in a face and two slices. The pieces of the front
face are shown.
16
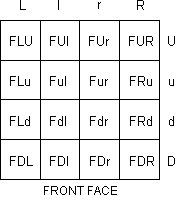 Obviously, this notation is awkward to implement on computers which have only upper case.
In such situations, one could use the next letter of the alphabet to represent a slice -
e.g. L, N, S, P; U, V, E, D; F, G, C, B.
Obviously, this notation is awkward to implement on computers which have only upper case.
In such situations, one could use the next letter of the alphabet to represent a slice -
e.g. L, N, S, P; U, V, E, D; F, G, C, B.
Some Sample Processes
I give a few sample processes to illustrate the notation and the way in which commutators
give simple processes. I will leave you to build a strategy from these.
[F, R] = (FLU, FUR)+ (RDF, RBD)- (FUl, FRu, DRf) (FUr, FRd, DRb)
[[F, R], L] = (FLU, ULB, RFU)
[[F, R], 1] = (FUl, UBl, DRf)
[U, r] = (ULb, UBr, FUr, DFr, RUb) (Ulb, Urb, Urf, Frd, Fru)
[[F, r], L] = (FLu, ULb, RFu)
[[F, r], l] = (Flu, Ulb, Drb)
![[[F,R],l]](images/cubic/cub3-13.gif) |
![[[F,r],L]](images/cubic/cub3-14.gif) |
| [[F,R],l] |
[[F,r],L] |
17
[[F, r], d'] = (Fru, Frd, Rbd)
[f,r] = (Luf, Urf, Frd) (Ruf, Drf, Brd)
[r,b] = (Fur, Ubr, Rbd) (Bur, Dbr, Lbd)
![[[F,r],d']](images/cubic/cub3-15.gif) |
![Half of [r,b]](images/cubic/cub3-16.gif) |
| [[F,r],d'] |
Half of [r,b] |
![[[r,b] ,F]](images/cubic/cub3-17.gif) [[r, b], F] = (Fru, Flu, Rbd)
[[r, b], F] = (Fru, Flu, Rbd)
Let me fill in this space by remarking that the 43 exhibits the properties of both the
23 and the 33, if you move halves or just faces. Thus one can obtain
a large number of patterns by using known patterns on the 33, together with certain
variations from the 23. In particular, one can obtain the cube in a cube in a
cube in a cube or quadruple cube pattern. It is not possible to get chessboards on all six
faces. I don't know if you can get stripes on all faces??
WINNING WAYS ON THE U GROUP
Winning Ways (= BCG) has appeared as noted in C2-4. The BCS Tables (pp.808-809) have been
revised and any U position can be restored in at most 29 moves (N49). David Seal has
shown that most of the results are best possible. The hardest patterns are (A, B) (b, d) (in any
orientation) and A+ C- a+ b+ c+ d+ requiring 13 and 16 moves.
.
18
THE 53
Pierre Bouchard sends an article from Journal de Montréal about a 53
invented by Gaston Saint-Pierre, a 21-year old Quebec boy. The first prototype was in wood,
14 inches (about 35 cm) on a side. He has built a prototype in aluminium, about 7 cm on a
side, which took 176 hours to make and weighs 2 pounds (about 1 kg). It has 99 pieces,
presumably 98 (= 125 - 27) exterior pieces and one interior piece. He estimates that it has
1090 positions and it takes him 1 1/4 hours to restore. Quite a number of
53 designs and patents have appeared, but this is the first working one I have
heard of.
 Let us work out a first guess as to the number of patterns on the 53. There
are 6 kinds of pieces, indicated in the diagram: A = corners; B = edges; C = edge middles;
D = inner corners; E = inner edges; F = centres. There are 8; 24; 12; 24; 24; 6 of these,
but pieces B, C, E are asymmetric so their orientation is determined by their position. The
constructible group thus has
Let us work out a first guess as to the number of patterns on the 53. There
are 6 kinds of pieces, indicated in the diagram: A = corners; B = edges; C = edge middles;
D = inner corners; E = inner edges; F = centres. There are 8; 24; 12; 24; 24; 6 of these,
but pieces B, C, E are asymmetric so their orientation is determined by their position. The
constructible group thus has
8!·38·24!·12!·212·24!·24!
= 123 96654 10985 74050 19981 53455 12384 81212 40682 69122
60338 23429 49382 61930 84194 48832 00000 00000 00000
= 1.24 × 1092 patterns.
Just as with the 33, the corners and edges have their total twist and flip
conserved so we will divide by 3 and 2. There are two kinds of moves: faces and offset
'slices'. Each of these gives a number of 4-cycles of pieces as tabulated.
| A | B | C | D | E |
| Face | 1 | 2 | 1 | 1 | 1 |
| Slice | 0 | 1 | 0 | 2 | 1 |
Consequently the parity of the A, C and D movements must all be the same, which gives
only 1/4 of the possible permutations of the positions. Now we also have 6 sets of four D
end E pieces which can be permuted without changing the appearance (assuming the faces are
uniformly coloured). However, the D pieces have the same parity as the A pieces, so only
half of the permutations of the D pieces are possible. Using commutators of the form
[X,[Y,Z]], just as on the 43, we can get 3-cycles of each type of piece, so we
can get all the patterns permitted by the above conservations. Thus there are
8!·38·24!·12!·212·24!·24! / (3·2·4·246·246/2)
= 28287 09422 77741 85653 61803 33107 15032 82931 27731 98567 21347 21536 00000 00000 00000
= 2.83 × 1074 patterns.
.
19
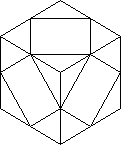
THE MAGIC DODECAHEDRON AND ALEXANDER'S STAR
The Magic Dodecahedron has been contemplated for some time. So far I have seen photos or
models from: Ben Halpern (USA), Boris Horvat (Yugoslavia), Barry Lockwood (UK) and
Miklós Kristóf (Hungary) while Kersten Meier (Germany) sent plans in early
1981. I have heard that Christoph Bandelow and Doctor Moll (Germany) have patents and that
Mario Ouellette and Luc Robillard (Canada) have both found mechanisms. The Hungarian version
15 notable as being in production (being exported by General Impex) and as having the planes
closer to the centre so each face has a star pattern.
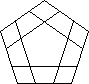 |
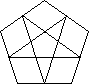 |
| Face patterns of the Dodecahedron |
Uwe Mèffert has bought the Halpern and Meier rights, which were both filed on the
same day about a month before Kristóf. However, there is an unresolved dispute over
the extent of overlap in the designs.
The theory of the Magic Dodecahedron is discussed elsewhere.
.
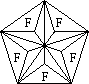 A simpler version of the dodecahedron is due to Adam Alexander, a US mathematician.
The shape is a great dodecahedron which is an icosahedron with its faces pushed in so
the pentagonal pyramid about each vertex becomes a five-pointed star sitting on a plane
and it can rotate on this plane (marked F).
A simpler version of the dodecahedron is due to Adam Alexander, a US mathematician.
The shape is a great dodecahedron which is an icosahedron with its faces pushed in so
the pentagonal pyramid about each vertex becomes a five-pointed star sitting on a plane
and it can rotate on this plane (marked F).
One can view this as a Magic Dodecahedron without corners (or centres)
.
Thus there are
30!/2 · 230/2 = 7 12032 72378 98958 11841 60204 98546 68800 00000
= 7.1 × 1040 patterns.
20
 The 'faces' of the star are the planes on which the rotations take place. They comprise
five triangular areas, marked F above. Now the 12 faces fall into 6 pairs of parallel faces.
Alexander makes the parallel faces have the same colour, giving just 6 colours. Hence there
are two pieces of each of 15 types and the number of patterns must be divided by
215/2. There are 60 rigid motions of a dodecahedron (reflections are excluded)
which form a group isomorphic to A5. (Exercise: Show you can inscribe 5 cubes in
a dodecahedron so a symmetry of the dodecahedron is a permutation of these cubes.) The rigid
motions are rotations of order 5, 3, 2 and it is readily checked that each of these can be
obtained as an achievable position of the edges when centres are fixed. I.e. the spots group
or the centres group (N46/47) is the whole group A5 of symmetries. Hence the
effect of the centres being unseen is to divide the number of patterns by 60 and there
are 30! · 214/60 = 72431 71425 27156 38411 62130 22720 00000
= 7.2 × 1029 patterns. The fact that the star has identical pieces means that
one can produce an apparent 2-cycle! The arrangement of colours in the solved state is
arbitrary, as can be seen by observing that two colours can be exchanged by 8 two-cycles
and two flips, so this is an achievable process. There are 6! = 720 ways to assign the 6
colours to the 6 axes, but we get to divide by 60 to obtain 12 distinct START colour
patterns. Alternatively, if we look at a white face, we can rotate to put blue in a
standard direction, and then the remaining 4 colours can be in any order, which seems to
give 24 START patterns. However looking at the opposite white face gives the mirror image
arrangement of colours so there are only 12 START patterns.
The 'faces' of the star are the planes on which the rotations take place. They comprise
five triangular areas, marked F above. Now the 12 faces fall into 6 pairs of parallel faces.
Alexander makes the parallel faces have the same colour, giving just 6 colours. Hence there
are two pieces of each of 15 types and the number of patterns must be divided by
215/2. There are 60 rigid motions of a dodecahedron (reflections are excluded)
which form a group isomorphic to A5. (Exercise: Show you can inscribe 5 cubes in
a dodecahedron so a symmetry of the dodecahedron is a permutation of these cubes.) The rigid
motions are rotations of order 5, 3, 2 and it is readily checked that each of these can be
obtained as an achievable position of the edges when centres are fixed. I.e. the spots group
or the centres group (N46/47) is the whole group A5 of symmetries. Hence the
effect of the centres being unseen is to divide the number of patterns by 60 and there
are 30! · 214/60 = 72431 71425 27156 38411 62130 22720 00000
= 7.2 × 1029 patterns. The fact that the star has identical pieces means that
one can produce an apparent 2-cycle! The arrangement of colours in the solved state is
arbitrary, as can be seen by observing that two colours can be exchanged by 8 two-cycles
and two flips, so this is an achievable process. There are 6! = 720 ways to assign the 6
colours to the 6 axes, but we get to divide by 60 to obtain 12 distinct START colour
patterns. Alternatively, if we look at a white face, we can rotate to put blue in a
standard direction, and then the remaining 4 colours can be in any order, which seems to
give 24 START patterns. However looking at the opposite white face gives the mirror image
arrangement of colours so there are only 12 START patterns.
.
21
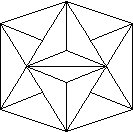
MAGIC POLYHEDRA
 For any polyhedron, or any planar graph, it is possible to imagine a magic version with
pieces at the vertices and edges 50 that each face turns. I have reported the work of
Andrew Taylor (N29) and Uldis Celmins (N60) on this. Here I outline the general result
which subsumes both works. If we have vertices of different valencies, i.e. with different
numbers of edges at them, then Andrew Taylor's idea (N29) is to imagine corner pieces with
the least common multiple (LCM) of the corner valencies. E.g. if we have valencies 3 and 4,
then corner pieces are 12-sided! See the diagram. One must then make some convention
regarding what effect face measurements have on corners. This is not critical as long as
the inverse of a move restores the pieces and the n-th power of an n-gonal face is the
identity. For convenience, I assume that turning face A will carry sector 0 to sector 0,
etc. That is, as we travel clockwise around the perimeter of A, the 0 sector is the one on
the right as we leave each vertex. Alternatively, we say that turning face A carries its
edges to its edges.
For any polyhedron, or any planar graph, it is possible to imagine a magic version with
pieces at the vertices and edges 50 that each face turns. I have reported the work of
Andrew Taylor (N29) and Uldis Celmins (N60) on this. Here I outline the general result
which subsumes both works. If we have vertices of different valencies, i.e. with different
numbers of edges at them, then Andrew Taylor's idea (N29) is to imagine corner pieces with
the least common multiple (LCM) of the corner valencies. E.g. if we have valencies 3 and 4,
then corner pieces are 12-sided! See the diagram. One must then make some convention
regarding what effect face measurements have on corners. This is not critical as long as
the inverse of a move restores the pieces and the n-th power of an n-gonal face is the
identity. For convenience, I assume that turning face A will carry sector 0 to sector 0,
etc. That is, as we travel clockwise around the perimeter of A, the 0 sector is the one on
the right as we leave each vertex. Alternatively, we say that turning face A carries its
edges to its edges.
Now we have some conservation theorems.
Theorem 1. If every face has an odd number of vertices, then each face turn (and
hence each achievable pattern) is an even permutation of corners and of edges. Otherwise
each turn is an even permutation of the corners and edges together.
Theorem 2. Only an even number of edge pieces can be flipped.
Chris Rowley has given me a simple proof.
Consider all S edges. Each of these has two sides or facelets. Each face turn is an even
permutation of the 2E facelets.
In order to deal with twists of corners, we must make some definitions following BCG and
Neumann. In the initial START position, assign a principal direction to each piece
and the same principal direction to its initial position. These directions correspond to
some sector of the piece.
22
For a piece in any position, its twist is the difference between the principal direction of
the piece and of the position that it is in. The twist is measured in units of 360°/v
where v is the LCM of all the corner valencies v0, and we work (mod v). There
is freedom to choose the sign of the twist, but we consider the orientation of the piece
with respect to its position and measure clockwise to agree with the previous usage in the
cycle representation. E.g. on the cube, we can take our principal directions as U and D.
Then if UHF is at BRU, we have a twist of +1. The total twist of a position is the
sum of all the twists (mod v). (Similar concepts hold for the edges, where v = 2.) The
total twist at START is 0.
Theorem 3. The total twist of corners is 0 (mod v) for any face turn (and hence
any achievable pattern). (A similar theorem holds for edges.)
Proof. Consider any face F and let its vertices be V1, V2, ...,
Ve in clockwise order. Label the sectors at each Vi by 0, 1, ..., v-1
so that F carries the sector at Vi into the same sector at Vi+1 -
e.g. as described above. Suppose the principal directions of the piece at Vi
and of the position Vi are sectors pi and qi in our
labelling. Then the twist at Vi is pi-qi and the
contribution of these pieces to the total twist is Sum(pi-qi)
(mod v).
23
Now F carries the piece at Vi to Vi+1 making the principal
direction of the piece at Vi+1 be pi while the principal direction of
the position Vi+1 remains qi+1. Thus the twist at
Vi+1 is pi-qi+1 and the contribution to the total twist
is Sum(pi-qi+1) (mod v), which is the same as the previous
contribution. Since all other pieces are fixed by F, the total twist has been preserved,
hence it always remains 0 (mod v).
I think the above is the clearest proof of theorem 3. I gather that Andrew Taylor's
approach was similar. However Taylor did not try to show all the permitted patterns were
achievable and thereby missed the next results, which are rather complex.
Theorem 4. If all Vi are even, then no edges can be flipped.
Proof. Because of the assumption, it is possible to colour the faces with two colours so
that adjacent faces have opposite colours. (Exercise - verify this.) Now each face turn
preserves the colouring, so that the colouring is always preserved and this fixes the
orientation of each edge piece.
The corresponding result for corners is a bit mere complex, but this argument works in
simple cases, such as the octahedron. If we build a magic octahedron and two-colour it, it
would always look the same.
Let kC = v/vC where vC is the valence of vertex C
and v = LCM{vC}. Let C and D be two adjacent vertices and set tCD
= kC + kD. Let d be the greatest common divisor (GCD) of v with the
set {tCD | C, D are adjacent vertices}
Theorem 5. A corner can only take on v/d of its possible positions.
 The proof here is based on the same idea as Theorem 4. We cyclically colour the v
sectors at vertex C with v/d copies of d colours. As we move the piece C about, we use it
to define the colouring at other vertices. Verifying the consistency of this colouring is
trickier than in Theorem 4 and is based on the fact that if F and G are two adjacent faces
at vertex C (as shown), then FG, which brings C back to C via D, imparts a twist of
-kC-kD to C. Since this is divisible by d, the colouring is
preserved.
The proof here is based on the same idea as Theorem 4. We cyclically colour the v
sectors at vertex C with v/d copies of d colours. As we move the piece C about, we use it
to define the colouring at other vertices. Verifying the consistency of this colouring is
trickier than in Theorem 4 and is based on the fact that if F and G are two adjacent faces
at vertex C (as shown), then FG, which brings C back to C via D, imparts a twist of
-kC-kD to C. Since this is divisible by d, the colouring is
preserved.
24
Example 1. The octahedron. Here all vC = 4, v = 4, all kC =
1 all tCD = 2, d = 2. The colouring is the same two-colouring mentioned above.
 Example 2. The infinite baby-blocks pattern. Here vC is alternately 3
and 6, v = 6, k is alternately 2 and 1, all tCD = 3, d = 3.
Example 2. The infinite baby-blocks pattern. Here vC is alternately 3
and 6, v = 6, k is alternately 2 and 1, all tCD = 3, d = 3.
The second half of the theory is to show that all the patterns permitted by the
conservation theorems can be achieved. This requires a moderate amount of calculation, the
exclusion of a number of degenerate cases and the separate consideration of
v >= 4, v = 3. The basic approach is to see that the Z and Y commutators have the same
structure as they have on the cube, although the twists on the cycles are replaced by
-kC-kD and kC+kD. For v > 4, we can use the
commutators to build up pairs of corner 2-cycles and corner twists and then edge 3-cycles
and pairs of edge flips. When v = 3, we combine the three Y commutators at a vertex as in
Benson's process (N24&45) to get 3 twists and 2 flips, whence any twisting and flipping
is obtained. Then we get 3-cycles of edges. Finally, we separately consider the tetrahedron
and all other cases to see that even permutation of corners can be achieved.
I believe the arguments work if we assume
- the graph is connected;
- two faces meet in at most one edge or at most one vertex;
- all faces have at least three edges.
These conditions are certainly satisfied for a polyhedron.
Now we can write down the number of patterns for a graph of V vertices, E edges,
v = LCM{vC}, d = GCD{v, tCD}, w= GCD{2, vC}, as
N = V! E! / (2 or 4) · (v/d)V-1 · (2/w)E-1
where 2 or 4 is 4 if all faces have an odd number of edges, 2 otherwise.
25
For the regular polyhedra of V vertices, E edges, valence v and e edges on each face, we
have kC = 1, tC = 2, d = w = GCD(2, v).
| V | E | v | e | 2 or 4 | d=w |
| Tetrahedron | 4 | 6 | 3 | 3 | 4 | 1 |
| Cube | 8 | 12 | 3 | 4 | 2 | 1 |
| Octahedron | 6 | 12 | 4 | 3 | 4 | 2 |
| Dodecahedron | 20 | 30 | 3 | 5 | 4 | 1 |
| Icosahedron | 12 | 30 | 5 | 3 | 4 | 1 |
| Tetrahedron | N = (4! 6! / 4) 33 25 | = | 37 32480 | |
| Cube | N = (8! 12! / 2) 37 211 | = | N (on N12) | |
| Octahedron | N = (6! 12! / 4) 25 | = | 275 90492 16000 | |
| Dodecahedron | N = (20! 30! / 4) 319 229 | = | 1006 69616 55352 33471 22516 03231 36455 05168 68811 64110 19768 62720 00000 00000 | = 1.01 × 1068 |
| Icosahedron | N = (12! 30! / 4) 511 229 | = | 83 26777 68427 04628 34605 13497 17691 92448 00000 00000 00000 00000 | = 8.33 × 1056 |
These results include both Taylor's and Celmin's results. However, the magic makers are
more masterful than mere mathematicians. With different shapes it is easier to make magic
with different styles of cutting. E.g. the Pyraminx has no centre pieces. This factors N by
the number of patterns in which only the centres move, or the number of symmetries of the
shape which are achievable patterns when the centres are ignored. Rubik and others have
shapes where faces have no edge pieces and movement moves some centres as well as edges.
Each of these gives rise to complications which will not be considered further here.
RUBIK ROBOTS
A group of students at the University of Illinois have built a robot called Robbie Rubik,
to solve the cube. The pattern must be entered into the computer however, - it does not have
a colour sensor. It only turns the top face - flippers and pistons turn the whole cube to
bring the appropriate face to the top. The computer is apparently programmed with my
algorithm - one of the students is holding a copy of my book in the photo.
Claude Shannon (of information theory fame) sent me an outline for a Rubik robot about
the beginning of this year.
26
PRETTY PATTERNS
I intended to include this material in C2, but there was too much other material. I have
several hundred, perhaps a thousand letters on my desk waiting to be read. Most of these
contain patterns. However, I find that the same patterns are rediscovered often, so I am
presenting what I have got so far in the hopes that it will answer some of the letters.
Sources
Several books have appeared which present a fair number of patterns. I haven't yet
collated all these, but let me list the books.
M. Razid Black & Herb Taylor. Unscrambling the Cube. Zephyr Engineering Design, PO
Box 1668, Burbank, California, 91507, USA. 40pp, 1980 (printed in 1981). (This includes
Black's earlier booklet: Constructing Patterns on the Cube.)
Mal Davies (227 Belly Oak Road, Kings Norton, Birmingham, P30 1HP, UK). Pretty Patterns.
2pp, 1981.
Don Taylor & Leanne Rylands. Cube Games. Penguin (UK), Holt Rinehart & Winston
(USA), Greenhouse (Australia). 54pp, 1981
French
A. Deledicq, J. C. Deledicq & J. B. Touchard. Le Cube - mode d'emploi. Editions
CEDIC. 47pp, 1981.
André Warusfel. Réussir le Rubik's Cube. Editions Denoël. 190pp,
1981.
German
Christoph Bandelow. Einführung in die Cubologie. Vieweg. 144pp, 1981.
Josef Trajber. Der Würfel fur Fortgeschrittene. Falken Verlag. 144pp, 1981.
Tom Werneck. Der Zauberwürfel fur Könner. Heyne Verlag. 160pp, 1982.
Generalities
I will adapt the presentation of patterns to give both the number of moves (as before)
and the number of quarter turns. E.g. 8,16q will mean 8 turns, but 16 quarter turns (i.e.
90° moves).
A. H. (Sandy) Frey has extended the notation to include moves of the whole cube, as
follows. Consider making a R face turn. If we let go of the rest of the cube, then the
whole cube turns with the R face. We denote this move by R. Don Taylor points out
that this puts us into a larger group - the oriented group - which has 24N = 10 38048
07858 77565 44000 patterns and that processes which only appear to be commutators when
we change coordinate systems (e.g. in the slice group) will now appear naturally as
commutators. For example, the 6-spot RsFsUsRs
is written RDR'D' = [R,D] in slice notation. This becomes [RsR',
DsD'] in our new notation. That is, a slice move R (in slice coordinates)
is equal to RsR' in our new notation. Some authors prefer to call
RsR' the R slice move, viewing the slice as moved clockwise, rather
than the R face. I will not use the notation very often, but there are situations where
it is very useful. Whole cube moves do not count as turns since they are part of the
process of moving from one turn to the next and do not take any extra time to execute.
27
Orbit names
Neil J Rubenking suggests names for the 12 orbits of the cube within the constructible
group. I have changed Switch to Swap. Start, Flip, Plus, Minus, Swap, Flip Plus, ... ,
Flip Swap Minus.
Diagonal Patterns
William J. Blewitt asked if there was any pattern with diagonals on all six faces.
John Butler sent an elegant example in a Twist orbit (i.e. in Plus or Minus). Consider
alternate vertices of the cube. These are the vertices of a regular tetrahedron whose
six edges are diagonals of the six cube faces. Imagine this tetrahedron rotated by
120° about a main diagonal of the cube. This pattern is readily obtained by the
corner 3-cycle on N25, followed by a 6-spot and then a corner twist.
 I posed Blewitt's question in an article and John O. Kiltinen of Northern Michigan
University has sent a solution. His argument is based entirely on the corners so it is
most easily expressed in terms of the 23 On the 23, a diagonal face
has the shown pattern, which is also a chessboard pattern. Then Kiltinen's result is that
there is no 6-diagonal pattern on the 23.
I posed Blewitt's question in an article and John O. Kiltinen of Northern Michigan
University has sent a solution. His argument is based entirely on the corners so it is
most easily expressed in terms of the 23 On the 23, a diagonal face
has the shown pattern, which is also a chessboard pattern. Then Kiltinen's result is that
there is no 6-diagonal pattern on the 23.
Proof. Take URF as fixed. Consider the UBL position, which would have to have a
U face in its U direction, assuming that such a pattern exists. If UBR is at UBL, then the
piece at DRB must have two R facelets. Similarly, UFL cannot be at UBL, so we must have
UBL at UBL. Likewise, DRB must be at DRB and DLF must be at DLF. So the four corners URF,
UBL, DRB, DLF must be a correct tetrahedron of pieces.
By the same argument, the other four corners are a correct tetrahedron of pieces, but
the two tetrahedra are not correct with respect to each other. Taking the first tetrahedron
as fixed, we need only consider the group S4 of 24 permutations of the other
corners, which correspond to the rigid motions (including reflections) of the second
tetrahedron. The reflections can be excluded at once since they reverse the colours on the
corner pieces. So we have just the group A4 of 12 even permutations, which
correspond to the rotations of the tetrahedron. One of these is the identity I. Eight of
these are 3-cycles corresponding to rotations about a cube diagonal and involve a twist of
a corner, so are impossible. The other three are pairs of 2-cycles corresponding to
rotations about a 'midline' of the tetrahedron, which is a face to face axis of the cube.
This leaves two edges of the tetrahedron in place and hence leaves two faces of the cube
of one colour. These are the zig-zag patterns which have four diagonal faces.
(The beginning of the argument is Kiltinen's. I have brought in the consideration of
S4 and A4 which allows us to deduce that the only 'generalised
diagonal' patterns (i.e. 6-diagonal patterns where a = b can occur) are START and Zig-Zag.
This also shows that one cannot get 6 chessboards on the 43.)
28
Two-face Patterns
Michael Holroyd points out that his 2-X on N53 is more efficient than the one on N47.
This 2-X was also discovered by G. Kéri and Charles Marks and other variations come
from Kevin Lewis and Ross & Karl Anderson.
| 2-X |
F2L2F2L2R2F2L2B2 |
(M. Holroyd & WK - 8, 16q; N8,47,53) |
| R2F2sR2·B2Rs2B2 |
(K. Lewis - 8, 16q; N8,47,53) |
| R2F2L2B2F2R2F2B2 |
(R. & K. Anderson - 8, 16q; N8,47,53) |
The last is Crossbars (N48) followed by Fs2 end is a conjugate of
Holroyd's method.
Four-face Patterns
There are two 4+ patterns. One rotates the corners 180° about a face axis, which I
take as UD (N48), and the other rotates by 900 about the UD axis and I take the clockwise
form.
| 4+ (180°) |
R2sU2R2s·F2sD2Fs2 |
(H. & K. Anderson - 10, 20q; N11,21,33,35,47,48) |
| UaFaUa2FaUaRa2 |
(A. Treep - 12, 16q; N11,21,33,35,47,48) |
| 4+ (90°) |
Rs2U2Fs2D . Rs2D2Fs2U' |
(V. Toth & L. Varga - 12, 22q; N48) |
The H face pattern is the same as the I face pattern seen sideways. H faces are easily
obtained from processes like (UF,UB)(DF,DB), but these yield 4-H patterns corresponding to
180° rotations. We also get 4-H patterns from 4+ patterns by a slice move.
| 4-H (180°) |
= 4+ (180°)·Us2 |
|
Rs2U2Rs2·Fs2D2Fs2·Us2 |
(GK, DBS & WK - 12, 24q ) |
|
(This is a conjugate of two uses of the second process in 5.8-D on N45.) |
| 4-H (90°) | = 4+ (90°)·U's |
|
Rs2U2Fs2DRs2D2Fs2U2D |
(GK - 13,24q) |
29
There are several 4-T patterns and the two obvious ones can be
converted to 4-U patterns by a U turn (though the Us are upside down).
| 4-U (180°) |
RaU2Ra'·FaU2Fa' |
(DBS - 10,12q; N49) |
| 4-T (180°) |
RaU2Ra'·FaU2Fa'·U2 |
(E. Fuss - 11,14q) |
| |
| Edgar Fuss calls the upside down 4-U a 'Temple' and it does look like a temple or
table with doors in the centre of each face. The 4-T can be viewed as a Temple with its
pillars in the centre of each face rather than at the corners. Fuss gives a friend's method
for 90° versions of these and two shorter methods have been received. |
| 4-U (90°) |
([R,U]U)7 |
(? - 28, 28q) |
|
FaU'Fa'URaURa'U'FaUFa'U'·U2 |
(H. Walker - 19,20q) |
|
RUs'B'D'BUsR'DLFRUsF'L'B' |
(B. G. Jones - 18,18q) |
| |
| David B. Shapiro sends a different 4-T arrangement which has the T's sideways with the
crosspieces adjacent. I have reduced this from 28 moves to 8 moves. |
| 4-T (sideways) |
L2FR2Us2L2BR2 |
(D. B. Shapiro & DBS - 8,14q) |
| |
| There is also a sideways version of 4-U. |
| 4-U (sideways) |
UsR2UsF2 |
(A. Treep - 6,8q) |
| |
| The 4-X pattern is easily obtained from 4-bar followed by Us2 |
| 4-X |
(R2F2L2)2Us2 |
(R. & K. Anderson, GK & WK - 8,16q; N47, 48) |
|
RaUa2RaU2Ra2U2 |
(A. Treep - 10,16q; N47,48) |
| |
| Frank O'Hara sends a shorter 4-Z and K. P. Furness sends a 4-2L pattern which is the
slice 4-flip (N31, 35, 36, 45, 47) followed by Fa. |
| 4-S |
FaRa'FaRaFa'Ra |
(F. O'Hara - 12,12q; N11,21,47) |
| 4-2L |
Fs2LF2UsR2BRs2F'L2Us'B2R'Fa |
(K. P. Furness - 18,24q) |
| |
| Six-face Patterns |
| |
| One can get Hs or Is on all six faces in several ways. The most symmetric is to have the
bars mutually orthogonal. Someone suggested this 6-H pattern be called the Irish cube (i.e.
the H-block!). |
| 6-H |
RaFaRaFa2RaFaRa |
(A. Treep - 14, 16q) |
| |
| Several people have sent 6-T patterns. Interestingly, these all give the same
asymmetrical arrangement. Exercise. Is there any other 6-T pattern? |
| 6-T |
(LsF2) 2 (D2B2) 3 |
(R. Ager - 12, 20q) |
|
LsF2LsD2F2U2B2U2 |
(F. Schmidt - 10, 16q) |
Miroslav Goljan and Jiri Fridrich have analysed the 6-U patterns and found 10 types. I
have their processes for 6 types, one of which is Pretzel's, for which Richard Walker has
a shorter version. Since these patterns are easier to describe as though the centres move
and the corners are fixed, I will do so. E.g. (F,U) means the F and U centres are exchanged.
Note that any pattern is even on centres and edges together (N46-47). This representation
must be treated carefully!
30
| a) |
R'D'B'D2FaRa D2Ra'F'DRFs'DaRs2Da' |
= (F B)(R,D)(U,L)LU+RD+(FD,BD) |
(22, 26q) |
| b) |
R'B'RsF'R'U'RFRs'BLB2Rs'U' |
= (F,R)(L,B)(U,D)(UF,DF,UR)(UL,UB) |
(22,26q) |
| c) |
R'B'RsF'R'DsBRBs'LFD2Bs'L2 |
= (F,L)(R,B)(U,D)(UF,UL)(UR,DB,UB) |
(18,20q) |
| d) |
LDBsR'FL'F'DsRFR'D' |
= (F,U,R)(B,D,L)(UF,RU)+ (DB,LB)+ |
(14,14q) |
| e) |
DaLFD'FLFUFs'L'F'D'B'DF'L'U2FsRsDs |
= (F,D,R)(B,U,L)(FR,DR,DF)+ (LB,LU,BU)+ |
(25,26q) |
| f) |
Rs·U'F(UF)2(U'F')2·Rs'·RsFsUsRs
= Rs·U'F(UF)2U'F'U'B'UsRs |
= (F,R,U)(B,L,D)(FL,RD,UB) |
(R. Walker - 16,16q; N49) |
The last three can be formed by moving the edges and then applying a 6-spot.
| There is a possible 6-bar pattern obtained by applying Rs to the 4-bar, but
the bars are not all orthogonal as described at N28, 47. |
| 6-bar |
RaU2Ra2U2R2 |
(A. Treep - 7,12q) |
More interestingly, Ross end Karl Anderson suggest R2F2L2R2F2Us2L2Us2
which almost gives the impossible 6-bar and if you hold it with your thumb and forefinger covering the F and B centres, then it looks like the impossible 6-bar.
| Kate Fried has found a 6-flip. |
| 6-flip |
(LFL'U)5 |
= UL+UB+UR+UF+FR+FD+ |
(K. Fried - 20,20q) |
| Conjugating this with F changes FD+ to FL+ and then the non-flipped edges are in the same
configuration as the flipped ones. |
 Mel Perry and Charles Marks send a new face pattern as shown. Marks calls this
'pinwheel' and I called it 'spiral'. The pinwheel comes in two orientations. Let us
call the depicted one 'clockwise' and its reflection 'anticlockwise'. Perry's pattern has
4 pinwheels in one direction and 2, on opposite faces, in the other direction, Marks has 5
pinwheels in one direction. Neither has a simple pattern-producing process.
Mel Perry and Charles Marks send a new face pattern as shown. Marks calls this
'pinwheel' and I called it 'spiral'. The pinwheel comes in two orientations. Let us
call the depicted one 'clockwise' and its reflection 'anticlockwise'. Perry's pattern has
4 pinwheels in one direction and 2, on opposite faces, in the other direction, Marks has 5
pinwheels in one direction. Neither has a simple pattern-producing process.
31
Exercises. Can we get 6 pinwheels in the same direction or 3 in each direction?
Are there patterns with a = c, b = d ?
David Sibley provides a process for producing tri-coloured faces.
S = S(U,R,F) = R'FD2F'D·L2·D'FD2F'R = (FUR,FLU)(BRU,BUL)(UR,LU)(LF,LB)
This exchanges the UR and LU columns and also (LF,LB). Applying this twice he obtains
a Tricolours where three faces use the same three colours in parallel columns. If
we use the mono-column-flip (N31,48), C = C(R,F,D) = R2FDR2D'R, we
can get the same pattern.
| Tricolours (Sibley) |
= S(U,R,F)·D·S(D,R,B)·U2D |
(D. Sibley - 25,32q) |
|
= C(R,D,B)U2C(R,D,B)-1 · C(F,U,L)D2C(F,U,L)-1 ·
UFs2U2Fs2U |
(D. Benson & DBS - 33,48q) |
You may find these easier to carry out if I write them as (SDR2)2UD2
and RCB2C'·FR2CB2C'·FRs2F2Rs2F
Joe Nemeth also found this pattern, but by a longer process.
Some Diagonal Patterns
Charles Marks send a number of patterns which led me to study ways of combining the
processes of Ahrens (N29) and Walker (N48) which twist corner 'pyramids', i.e. a corner
and its three adjacent edges considered as a unit. These give a number of diagonal face
patterns which I name as follows.
 |
 |
 |
 |
| Diagonal Tricolour |
Stairs |
Latin Square |
Quincolour |
A = A(U,R,F) = URF+(FU,UR,RF)UFL- = [R',F][U,F'][U',R]
twists the URF pyramid clockwise and the adjacent corner UFL anticlockwise.
W = W(U,R,F) = URF+(FU,UR,RF)DFR- ULB+(BU,UL,LF)DBL- = RaURa'·Fa'UFa
twists the URF and ULB pyramids clockwise and the adjacent corners DFR and DBL
anticlockwise.
Note that W = FR A R2 A RF'.
32
AU2F'LA'L' is a stage toward the Double-cube pattern (N28,29,48) and
is a 6-stairs pattern.
AUR'A' gives one diagonal tricolour, four stairs and a plain face (C. Marks)
.
Applying RU'(RaFa) 3 to this gives 5-diagonal
tricolours with one plain face (C. Marks - 36,36q)
.
This was the first case I saw of
a 5:1 distribution of face patterns. Usually one gets 3:3, 4:2 or 2:2:2, although the
first stage has 4:1:1 and Marks' Pinwheel is also a 5:1 (but came later). Marks says that
when he first made this, a friend picked it up and said "So you've got one face
correct".
WFU'AUF' followed by DBL-DFR+ gives three diagonal tricolours with their
diagonals radiating from UFL and three stairs with their bulk at DRF (C. Marks).
| [W, Fa'UFa UR2] |
= RaURa'Fa'U2FaU · Fa'D'FaRaD'Ra' · U'Fa'U'Fa |
(C. Marks - 27,28q) |
While considering the above pattern, I discovered a new 6-2L pattern. In this one, all
corners are in place, merely twisted, and no uprights adjacent.
(Note that 2L patterns are Pinwheels with a = b, c = d. This pattern has 6 anticlockwise
2Ls while the earlier 6-2L had 4 anticlockwise 2Ls.)
Marks says he can get two Latin square faces and the other four close to it.
Exercise. Is there any 6-Latin square pattern?
John O. Kiltinen sends a pattern consisting of 6-quincolours obtained by twisting the
corners of the 4 pyramids which are twisted in 6-diagonal tricolours. This can be achieved
by DWD'F2DW'D' (24,24q)
.
If one twists the corners in the opposite ways,
one gets the tricolour patterns which are quincolour with a = c = e.
The pattern given by (FLU,UBR,RDF)(FU,UR,RF)(FL,UB,RD)(FD,UL,RB)
takes the three pyramids
at FLU, UBR, RDF and rotates them as a unit 120° clockwise about the FUR-BLD axis. This
is a single pyramid twist away from Butler's impossible tetrahedron.
Miscellaneous Patterns
The Double-cube pattern (N28,29,48) can obviously be modified to a Triple-cube by
twisting the corners at the ends of the rotation axis. The faces can now all have two or
three colours. I can produce either of these in 32 moves by following Walker's process (N48)
with a conjugate of the U corner process +0-0.
.
David B. Shapiro sends a 'Flat meson' which consists of the two 23 at URF and ULB
rotated 180° about the UD axis. Turned over, it looks like a Temple with two corner
pillars or a two-legged table. It can be viewed as (UBR,UFL)(BR,FL) followed by D2, so it
could be easily obtained from the U process (A,C)(a,c).
.
Anneke Treep sends an odd but attractive pattern which she calls Skein. Form
UFR+DBL-UF+FR+RU+DB+BL+LD+ and then apply the 6-spot FsUsRsFs.
(Picture on next page.)
.
Pretty Random Patterns
A number of people seem more interested in disorder than order. There are several
different criteria that have been used to measure disorder. Let us consider the number of
facelets of each colour on a face and write down these numbers in decreasing order. We can
have 900000, 810000, 720000, 711000, ...
33
 We abbreviate these as 9 (= 905), 81, 72, 712 , .... The complete list of
these 'partitions of 9 into at most 6 parts' is:
9, 81, 72, 712, 63, 621, 613, 54, 531, 522, 5212,
514, 421, 432, 4312, 4221, 4213,
415, 33, 3221, 3213, 323,
32212, 3214, 2413,
2313. Of these, only 415, 3214,
2313 have all six colours.
We abbreviate these as 9 (= 905), 81, 72, 712 , .... The complete list of
these 'partitions of 9 into at most 6 parts' is:
9, 81, 72, 712, 63, 621, 613, 54, 531, 522, 5212,
514, 421, 432, 4312, 4221, 4213,
415, 33, 3221, 3213, 323,
32212, 3214, 2413,
2313. Of these, only 415, 3214,
2313 have all six colours.
David C. Maxwell and K. P. Furness both send
FaRaFaRa2 which gives six colours on
each face - four 2313and two 3213 - which is perhaps not
the most random distribution. Moreover, no two facelets of the same colour have a common
edge, so this is a proper colouring of the 54 facelets as a map. Brian Martin sends
(RsUs)2 which is a proper map colouring with six
4221 faces.
Charles Marks obtains six colours on each face without moving the edges: twist all the
U corners + and all the D corners - (e.g. by using the U corner process ++-- on the F and
B faces); apply Zig-zag (RaFa)3; exchange U and D edges
with a 2X pattern.
.
Brian Martin gets six 2313 faces by: 12-flip; diagonal exchange
of corners exchanging F & B (i.e. (FUR,BLD)(FLU,BDR)(FDL,BRU)(FRD,BUL)); then
FLU-FRD-BRU+BLD+.
.
This is also a proper map colouring. Indeed no two facelets of the same
colour meet at an edge or a corner, so it is a 'strong' map colouring. In fact, any two
cochromatic facelets on a face are separated by a knight's move (16 times) or are diagonal
corners (2 times). Frank Carey finds that (UL,LB,DL,RB)(UR,LF,DR,RF) UF+UB+DF+DB+ gives a
strong map colouring.
Entropy of a Pattern
George Marx and his colleagues in Budapest have used the Cube as a model for the physical
concept of entropy, which is a measure of disorder and is the logarithm of the number of
states of a given type. That is, the more common a type is, the greater its entropy, and
the most common types are generally those with the least structure, i.e. the maximum
disorder.
A simple example is to consider each of the 9 facelets of a face as being equally
likely to have each of the 6 colours, giving 69= 100 77696 equally likely
patterns. (This ignores the effects of the other faces.) If there are Ci
facelets of colour i, then there are 9!/C1! ... C6! ways to
distribute the 9 facelets in this colour pattern. However, we shall just consider the
'partition' of 9 given by the Ci, so we want to count all the different ways
the Ci can be rearranged - i.e. we consider all the possible reassignments of
colours. If there are Nj values of Ci which are equal to j, then
there are 6! / N0!...N9! distributions of the Ci for a
particular partition. For example, if we take the partition 712 , then the
corresponding distributions (or ordered partitions) are 711000, 710100, 710010, 710001,
..., 000117. Here N0 = 3, N1 = 2, ..., N7 = 1 and there
are
6! / 3!2!0!0!0!1! = 60 distributions corresponding to the partition 712
(=71203). Each of these distributions occurs 9! / 7!1!l!0!0!0! = 72
times as a distribution of facelets, so we have 72.60 = 4320 patterns for this partition.
Straightforward calculations show that the most common partition is
32212 which has 27 21600 patterns of the 69, which is
about 27% of them.
34
For the 23, the partitions of one face are 4, 31, 22,
212, 14
and they have 6, 120, 90, 720, 360 patterns respectively. On the 43 there
are 136 partitions of 16 into at most 6 parts. Exercise. Calculate the number of
patterns for each partition of a face on the 43.
Some Pretty Patterns in Other Orbits
The pattern of Walker's Snake (N49) followed by (FL,RB) has the appearance of the unique
type of circuit along edges through all the vertices of a cube. The pattern is reminiscent
of the curve on a tennis ball or a baseball. Such circuits are called Hamiltonian and so I
call this the Hamiltonian circuit or Tennis ball pattern. It is in the Swap
orbit. The Worm and the Snake are the only types of Hamiltonian circuits through the faces
of a cube, or, equivalently, through the vertices of an octahedron. Zig-zag can be viewed
as such a circuit along the edges of a tetrahedron, and is the only type of such circuit.
Edgar Fuss gives a Swap Double-cube pattern. Imagine the ordinary Double-cube (about
the FUR-BLD axis) and then rotate the two 23 180° about the LF-RB axis.
 Ray Ager tried to construct patterns with (2+1)2 faces, with a = d, b = c.
He can get it on four faces, with two 81 faces, by
U2R2U2R2U2B2R2U2.
I have found a version with a = d on six faces arranged to show (2+1)3.
The pattern is (FU,LU,BU)+ (RU,RB,RD)+ (FR,FD,FL)+ (FLU,LBU)+ (UBR,BDR)+ (FRD,FDL)+ which
is in Swap-Flip. Exercises. Is there any achievable (2+1)3? Is there any
constructible (2+1)3 with b = c (and a = d)? The name of this face pattern
derives from its being a geometric representation of (2+1)2 = 2·2 +
2·1 + 1·2 + 1·1.
Ray Ager tried to construct patterns with (2+1)2 faces, with a = d, b = c.
He can get it on four faces, with two 81 faces, by
U2R2U2R2U2B2R2U2.
I have found a version with a = d on six faces arranged to show (2+1)3.
The pattern is (FU,LU,BU)+ (RU,RB,RD)+ (FR,FD,FL)+ (FLU,LBU)+ (UBR,BDR)+ (FRD,FDL)+ which
is in Swap-Flip. Exercises. Is there any achievable (2+1)3? Is there any
constructible (2+1)3 with b = c (and a = d)? The name of this face pattern
derives from its being a geometric representation of (2+1)2 = 2·2 +
2·1 + 1·2 + 1·1.
ORDERS OF ELEMENTS
Several people have found that there are just 73 possible orders of elements (N50/50).
Jesper C. Gerved and Torben Maack Bisgaard, of Copenhagen, have computed the number of
elements of each order as shown in their Table 4 on the adjoining page. I find that the
average order is 122 and the median is 67.3. In ascending frequency of appearance, the
orders are:
1, 11, 2, 3, 5, 7, 22, 4, 55 & 110, 80, 15, 33, 14, 21, 1260, 9, 10, 35, 280, 28,
315, 44, 99, 720, 112, 6, 16, 495 & 990, 77, 154, 45, 20, 165, 330, 140, 105, 504, 840, 336, 63, 8, 70,
231 & 462, 630, 66; 240, 126, 18, 360, 132, 56, 252, 144, 42, 198, 48, 420, 168, 40, 210, 72, 84,
90, 120 30, 12, 180, 36, 24, 60.
About 10.6% of the positions have order 60.
35
| Order | | Number of elements | | Order | | Number of elements |
| 1 | | 1 | | 77 | | 187 23810 94133 76000 |
| 2 | | 17 09115 49183 | | 80 | | 13 34938 37266 94400 |
| 3 | | 3389 45406 22394 | | 84 | | 1697 72581 86780 67200 |
| 4 | | 4 34695 70301 44256 | | 90 | | 1925 06905 16173 83168 |
| 5 | | 13352 81725 14624 | | 99 | | 104 36790 91359 74400 |
| 6 | | 140 62105 92987 55526 | | 105 | | 232 82441 94233 54880 |
| 7 | | 15324 55171 48800 | | 110 | | 4 85432 13551 61600 |
| 8 | | 294 99863 89819 39200 | | 112 | | 128 72620 02216 96000 |
| 9 | | 55 33375 23984 28896 | | 120 | | 1947 04401 14631 47520 |
| 10 | | 65 25089 78363 52192 | | 126 | | 425 69635 22238 87360 |
| 11 | | 4 45906 94400 | | 132 | | 637 12967 78649 60000 |
| 12 | | 2330 23282 74555 54048 | | 140 | | 223 12541 37176 06400 |
| 14 | | 23 29837 43830 21440 | | 144 | | 714 19202 93781 50400 |
| 15 | | 14 38547 13332 09856 | | 154 | | 187 23810 94133 76000 |
| 16 | | 150 73188 62708 73600 | | 165 | | 213 59013 96271 10400 |
| 18 | | 520 62284 91581 24832 | | 168 | | 1050 26923 92665 08800 |
| 20 | | 198 73224 56649 27744 | | 180 | | 2453 88900 57383 11680 |
| 21 | | 39 33715 15593 33120 | | 198 | | 759 70129 20827 90400 |
| 22 | | 92708 51272 70400 | | 210 | | 1339 23273 20469 50400 |
| 24 | | 3293 93251 97962 44480 | | 231 | | 374 47621 88267 52000 |
| 28 | | 97 41976 09076 73600 | | 240 | | 407 15620 36641 79200 |
| 30 | | 2033 28420 89667 40224 | | 252 | | 689 87708 04473 85600 |
| 33 | | 15 87401 96622 33600 | | 280 | | 68 65397 34515 71200 |
| 35 | | 65 52621 89125 63200 | | 315 | | 99 30987 96525 15840 |
| 36 | | 3186 20259 79731 76320 | | 330 | | 213 59013 96271 10400 |
| 40 | | 1136 25838 02544 12800 | | 336 | | 257 45240 04433 92000 |
| 42 | | 737 19977 68310 97600 | | 360 | | 571 01988 89093 52960 |
| 44 | | 100 12037 79502 08000 | | 420 | | 961 15562 83219 96800 |
| 45 | | 197 32944 16597 27104 | | 462 | | 374 47621 88267 52000 |
| 48 | | 911 49764 74103 80800 | | 495 | | 174 75556 87858 17600 |
| 55 | | 4 85432 13551 61600 | | 504 | | 238 38185 22624 00000 |
| 56 | | 671 20530 68464 12800 | | 630 | | 395 38014 01624 16640 |
| 60 | | 4601 52469 28929 25952 | | 720 | | 120 14445 35402 49600 |
| 63 | | 264 37143 37053 08160 | | 840 | | 240 28890 70804 99200 |
| 66 | | 404 05117 52503 29600 | | 990 | | 174 75556 87858 17600 |
| 70 | | 353 49083 42737 30560 | | 1260 | | 51 49048 00886 78400 |
| 72 | | 1681 09266 03396 71040 | | | | |
Table 4. The number of elements of each possible order in the group Go
36
THE MAGIC DISC
 In N51/52, I discussed planar versions of the Magic Cube. During my recent visit to
Budapest, Tibor Szentiványi gave me a Magic Disc which is a different kind of planar
magic cube. It comprises a circular disc divided into two halves (A and B) surrounded by a
ring of 6 pieces (1 to 6). The outer ring rotates with respect to the inner ring. Further,
when aligned as shown, the right half of the disc can be turned over, exposing the reverse
sides B', 1', 2', 3' as shown. The two sides have pictures of dogs in blue and brown and
they are not easy to keep track of. If we hold it with A up, there are only 1152 distinct
patterns and these readily reduce to 96. I find the diameter of the reduced Cayley graph
is 7 and there are nine antipodes. Despite the simplicity of the problem, it is not trivial
to produce an algorithm nor to determine just what patterns are possible. If the outer ring
of the disc has only 4 parts, then there are 48 patterns which reduce to 6, where the
Cayley graph is a 6-cycle. The case with 2n parts, for n≠3, is quite different to the 6
part case.
In N51/52, I discussed planar versions of the Magic Cube. During my recent visit to
Budapest, Tibor Szentiványi gave me a Magic Disc which is a different kind of planar
magic cube. It comprises a circular disc divided into two halves (A and B) surrounded by a
ring of 6 pieces (1 to 6). The outer ring rotates with respect to the inner ring. Further,
when aligned as shown, the right half of the disc can be turned over, exposing the reverse
sides B', 1', 2', 3' as shown. The two sides have pictures of dogs in blue and brown and
they are not easy to keep track of. If we hold it with A up, there are only 1152 distinct
patterns and these readily reduce to 96. I find the diameter of the reduced Cayley graph
is 7 and there are nine antipodes. Despite the simplicity of the problem, it is not trivial
to produce an algorithm nor to determine just what patterns are possible. If the outer ring
of the disc has only 4 parts, then there are 48 patterns which reduce to 6, where the
Cayley graph is a 6-cycle. The case with 2n parts, for n≠3, is quite different to the 6
part case.
COMMENTS ON THE U GROUP
Guus Razoux Schultz has a method for the U group (N49) in at most 26 moves. Jerome
Jean-Charles conjectures its diameter is 19q.
© David Singmaster
The text and original drawings are copyright © David Singmaster, reproduced here with
permission. Conversion to html and additional commentary by Jaap Scherphuis.
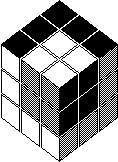


 Mondadori, the Italian distributor of the cube, is doing two variants. The Fifteen Cubo
is a Magic Square Magic Cube with black numbers on gold labels. (See
Mondadori, the Italian distributor of the cube, is doing two variants. The Fifteen Cubo
is a Magic Square Magic Cube with black numbers on gold labels. (See  Another variant is the Banana Puzzler which has six colours of bananas on white labels
and the box says "This puzzler will drive you bananas". Peter Redmill sends a
different type of edge colouring. He has each face split in half. The halves can be viewed
as corresponding to edges. There is a way to colour the edges with four colours so the
three colours of each edge are along three orthogonal intersecting edges, as shown.
Another variant is the Banana Puzzler which has six colours of bananas on white labels
and the box says "This puzzler will drive you bananas". Peter Redmill sends a
different type of edge colouring. He has each face split in half. The halves can be viewed
as corresponding to edges. There is a way to colour the edges with four colours so the
three colours of each edge are along three orthogonal intersecting edges, as shown.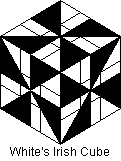 Henry and Bruce Dan, of Atlanta, Georgia, have been making solid colour cubes by buying
lots of ordinary cubes and peeling the labels. (They could have bought white or black cubes
directly from Ideal!) The Taiwanese have sold a black cube as The Executive Polish Cube.
"Its total lack of reason for being will keep you fascinated for several minutes, or,
perhaps, only a few seconds ... try to solve the puzzle with your eyes closed ... work the
puzzle in the dark."
Henry and Bruce Dan, of Atlanta, Georgia, have been making solid colour cubes by buying
lots of ordinary cubes and peeling the labels. (They could have bought white or black cubes
directly from Ideal!) The Taiwanese have sold a black cube as The Executive Polish Cube.
"Its total lack of reason for being will keep you fascinated for several minutes, or,
perhaps, only a few seconds ... try to solve the puzzle with your eyes closed ... work the
puzzle in the dark."



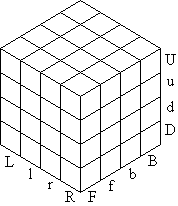 Kurt Endl has proposed a notation using A, B, C, D, 1, 2, 3, 4; I, II, III, IV to
represent the levels in a 43. This has the advantage of being indefinitely
expandable, but I prefer a notation which retains some mnemonic character like the B, L, U,
D, F, B notation for the 43 . I find the following seems to be the most
convenient for me. Label the 'slice' layer adjacent to each face by the lover case letter
of that face. Thus the four levels from left to right are denoted L, l, r, R as shown in
the diagram. Similarly we use U, u, d, D and F, f, b, B. Because we do not have centre
pieces, one must be careful physically to remember which directions are which, or one can
keep a corner fixed, as with the 23 (N53).
Kurt Endl has proposed a notation using A, B, C, D, 1, 2, 3, 4; I, II, III, IV to
represent the levels in a 43. This has the advantage of being indefinitely
expandable, but I prefer a notation which retains some mnemonic character like the B, L, U,
D, F, B notation for the 43 . I find the following seems to be the most
convenient for me. Label the 'slice' layer adjacent to each face by the lover case letter
of that face. Thus the four levels from left to right are denoted L, l, r, R as shown in
the diagram. Similarly we use U, u, d, D and F, f, b, B. Because we do not have centre
pieces, one must be careful physically to remember which directions are which, or one can
keep a corner fixed, as with the 23 (N53). Obviously, this notation is awkward to implement on computers which have only upper case.
In such situations, one could use the next letter of the alphabet to represent a slice -
e.g. L, N, S, P; U, V, E, D; F, G, C, B.
Obviously, this notation is awkward to implement on computers which have only upper case.
In such situations, one could use the next letter of the alphabet to represent a slice -
e.g. L, N, S, P; U, V, E, D; F, G, C, B.![[[F,R],l]](images/cubic/cub3-13.gif)
![[[F,r],L]](images/cubic/cub3-14.gif)
![[[F,r],d']](images/cubic/cub3-15.gif)
![Half of [r,b]](images/cubic/cub3-16.gif)
![[[r,b] ,F]](images/cubic/cub3-17.gif) [[r, b], F] = (Fru, Flu, Rbd)
[[r, b], F] = (Fru, Flu, Rbd) Let us work out a first guess as to the number of patterns on the 53. There
are 6 kinds of pieces, indicated in the diagram: A = corners; B = edges; C = edge middles;
D = inner corners; E = inner edges; F = centres. There are 8; 24; 12; 24; 24; 6 of these,
but pieces B, C, E are asymmetric so their orientation is determined by their position. The
constructible group thus has
Let us work out a first guess as to the number of patterns on the 53. There
are 6 kinds of pieces, indicated in the diagram: A = corners; B = edges; C = edge middles;
D = inner corners; E = inner edges; F = centres. There are 8; 24; 12; 24; 24; 6 of these,
but pieces B, C, E are asymmetric so their orientation is determined by their position. The
constructible group thus has

 A simpler version of the dodecahedron is due to Adam Alexander, a US mathematician.
The shape is a great dodecahedron which is an icosahedron with its faces pushed in so
the pentagonal pyramid about each vertex becomes a five-pointed star sitting on a plane
and it can rotate on this plane (marked F).
A simpler version of the dodecahedron is due to Adam Alexander, a US mathematician.
The shape is a great dodecahedron which is an icosahedron with its faces pushed in so
the pentagonal pyramid about each vertex becomes a five-pointed star sitting on a plane
and it can rotate on this plane (marked F).
 The 'faces' of the star are the planes on which the rotations take place. They comprise
five triangular areas, marked F above. Now the 12 faces fall into 6 pairs of parallel faces.
Alexander makes the parallel faces have the same colour, giving just 6 colours. Hence there
are two pieces of each of 15 types and the number of patterns must be divided by
215/2. There are 60 rigid motions of a dodecahedron (reflections are excluded)
which form a group isomorphic to A5. (Exercise: Show you can inscribe 5 cubes in
a dodecahedron so a symmetry of the dodecahedron is a permutation of these cubes.) The rigid
motions are rotations of order 5, 3, 2 and it is readily checked that each of these can be
obtained as an achievable position of the edges when centres are fixed. I.e. the spots group
or the centres group (N46/47) is the whole group A5 of symmetries. Hence the
effect of the centres being unseen is to divide the number of patterns by 60 and there
are 30! · 214/60 = 72431 71425 27156 38411 62130 22720 00000
= 7.2 × 1029 patterns. The fact that the star has identical pieces means that
one can produce an apparent 2-cycle! The arrangement of colours in the solved state is
arbitrary, as can be seen by observing that two colours can be exchanged by 8 two-cycles
and two flips, so this is an achievable process. There are 6! = 720 ways to assign the 6
colours to the 6 axes, but we get to divide by 60 to obtain 12 distinct START colour
patterns. Alternatively, if we look at a white face, we can rotate to put blue in a
standard direction, and then the remaining 4 colours can be in any order, which seems to
give 24 START patterns. However looking at the opposite white face gives the mirror image
arrangement of colours so there are only 12 START patterns.
The 'faces' of the star are the planes on which the rotations take place. They comprise
five triangular areas, marked F above. Now the 12 faces fall into 6 pairs of parallel faces.
Alexander makes the parallel faces have the same colour, giving just 6 colours. Hence there
are two pieces of each of 15 types and the number of patterns must be divided by
215/2. There are 60 rigid motions of a dodecahedron (reflections are excluded)
which form a group isomorphic to A5. (Exercise: Show you can inscribe 5 cubes in
a dodecahedron so a symmetry of the dodecahedron is a permutation of these cubes.) The rigid
motions are rotations of order 5, 3, 2 and it is readily checked that each of these can be
obtained as an achievable position of the edges when centres are fixed. I.e. the spots group
or the centres group (N46/47) is the whole group A5 of symmetries. Hence the
effect of the centres being unseen is to divide the number of patterns by 60 and there
are 30! · 214/60 = 72431 71425 27156 38411 62130 22720 00000
= 7.2 × 1029 patterns. The fact that the star has identical pieces means that
one can produce an apparent 2-cycle! The arrangement of colours in the solved state is
arbitrary, as can be seen by observing that two colours can be exchanged by 8 two-cycles
and two flips, so this is an achievable process. There are 6! = 720 ways to assign the 6
colours to the 6 axes, but we get to divide by 60 to obtain 12 distinct START colour
patterns. Alternatively, if we look at a white face, we can rotate to put blue in a
standard direction, and then the remaining 4 colours can be in any order, which seems to
give 24 START patterns. However looking at the opposite white face gives the mirror image
arrangement of colours so there are only 12 START patterns.
 For any polyhedron, or any planar graph, it is possible to imagine a magic version with
pieces at the vertices and edges 50 that each face turns. I have reported the work of
Andrew Taylor (N29) and Uldis Celmins (N60) on this. Here I outline the general result
which subsumes both works. If we have vertices of different valencies, i.e. with different
numbers of edges at them, then Andrew Taylor's idea (N29) is to imagine corner pieces with
the least common multiple (LCM) of the corner valencies. E.g. if we have valencies 3 and 4,
then corner pieces are 12-sided! See the diagram. One must then make some convention
regarding what effect face measurements have on corners. This is not critical as long as
the inverse of a move restores the pieces and the n-th power of an n-gonal face is the
identity. For convenience, I assume that turning face A will carry sector 0 to sector 0,
etc. That is, as we travel clockwise around the perimeter of A, the 0 sector is the one on
the right as we leave each vertex. Alternatively, we say that turning face A carries its
edges to its edges.
For any polyhedron, or any planar graph, it is possible to imagine a magic version with
pieces at the vertices and edges 50 that each face turns. I have reported the work of
Andrew Taylor (N29) and Uldis Celmins (N60) on this. Here I outline the general result
which subsumes both works. If we have vertices of different valencies, i.e. with different
numbers of edges at them, then Andrew Taylor's idea (N29) is to imagine corner pieces with
the least common multiple (LCM) of the corner valencies. E.g. if we have valencies 3 and 4,
then corner pieces are 12-sided! See the diagram. One must then make some convention
regarding what effect face measurements have on corners. This is not critical as long as
the inverse of a move restores the pieces and the n-th power of an n-gonal face is the
identity. For convenience, I assume that turning face A will carry sector 0 to sector 0,
etc. That is, as we travel clockwise around the perimeter of A, the 0 sector is the one on
the right as we leave each vertex. Alternatively, we say that turning face A carries its
edges to its edges.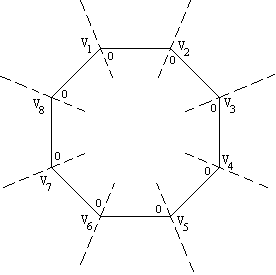
 The proof here is based on the same idea as Theorem 4. We cyclically colour the v
sectors at vertex C with v/d copies of d colours. As we move the piece C about, we use it
to define the colouring at other vertices. Verifying the consistency of this colouring is
trickier than in Theorem 4 and is based on the fact that if F and G are two adjacent faces
at vertex C (as shown), then FG, which brings C back to C via D, imparts a twist of
-kC-kD to C. Since this is divisible by d, the colouring is
preserved.
The proof here is based on the same idea as Theorem 4. We cyclically colour the v
sectors at vertex C with v/d copies of d colours. As we move the piece C about, we use it
to define the colouring at other vertices. Verifying the consistency of this colouring is
trickier than in Theorem 4 and is based on the fact that if F and G are two adjacent faces
at vertex C (as shown), then FG, which brings C back to C via D, imparts a twist of
-kC-kD to C. Since this is divisible by d, the colouring is
preserved. Example 2. The infinite baby-blocks pattern. Here vC is alternately 3
and 6, v = 6, k is alternately 2 and 1, all tCD = 3, d = 3.
Example 2. The infinite baby-blocks pattern. Here vC is alternately 3
and 6, v = 6, k is alternately 2 and 1, all tCD = 3, d = 3. I posed Blewitt's question in an article and John O. Kiltinen of Northern Michigan
University has sent a solution. His argument is based entirely on the corners so it is
most easily expressed in terms of the 23 On the 23, a diagonal face
has the shown pattern, which is also a chessboard pattern. Then Kiltinen's result is that
there is no 6-diagonal pattern on the 23.
I posed Blewitt's question in an article and John O. Kiltinen of Northern Michigan
University has sent a solution. His argument is based entirely on the corners so it is
most easily expressed in terms of the 23 On the 23, a diagonal face
has the shown pattern, which is also a chessboard pattern. Then Kiltinen's result is that
there is no 6-diagonal pattern on the 23.


 Mel Perry and Charles Marks send a new face pattern as shown. Marks calls this
'pinwheel' and I called it 'spiral'. The pinwheel comes in two orientations. Let us
call the depicted one 'clockwise' and its reflection 'anticlockwise'. Perry's pattern has
4 pinwheels in one direction and 2, on opposite faces, in the other direction, Marks has 5
pinwheels in one direction. Neither has a simple pattern-producing process.
Mel Perry and Charles Marks send a new face pattern as shown. Marks calls this
'pinwheel' and I called it 'spiral'. The pinwheel comes in two orientations. Let us
call the depicted one 'clockwise' and its reflection 'anticlockwise'. Perry's pattern has
4 pinwheels in one direction and 2, on opposite faces, in the other direction, Marks has 5
pinwheels in one direction. Neither has a simple pattern-producing process.




 We abbreviate these as 9 (= 905), 81, 72, 712 , .... The complete list of
these 'partitions of 9 into at most 6 parts' is:
9, 81, 72, 712, 63, 621, 613, 54, 531, 522, 5212,
514, 421, 432, 4312, 4221, 4213,
415, 33, 3221, 3213, 323,
32212, 3214, 2413,
2313. Of these, only 415, 3214,
2313 have all six colours.
We abbreviate these as 9 (= 905), 81, 72, 712 , .... The complete list of
these 'partitions of 9 into at most 6 parts' is:
9, 81, 72, 712, 63, 621, 613, 54, 531, 522, 5212,
514, 421, 432, 4312, 4221, 4213,
415, 33, 3221, 3213, 323,
32212, 3214, 2413,
2313. Of these, only 415, 3214,
2313 have all six colours. Ray Ager tried to construct patterns with (2+1)2 faces, with a = d, b = c.
He can get it on four faces, with two 81 faces, by
U2R2U2R2U2B2R2U2.
I have found a version with a = d on six faces arranged to show (2+1)3.
The pattern is (FU,LU,BU)+ (RU,RB,RD)+ (FR,FD,FL)+ (FLU,LBU)+ (UBR,BDR)+ (FRD,FDL)+ which
is in Swap-Flip. Exercises. Is there any achievable (2+1)3? Is there any
constructible (2+1)3 with b = c (and a = d)? The name of this face pattern
derives from its being a geometric representation of (2+1)2 = 2·2 +
2·1 + 1·2 + 1·1.
Ray Ager tried to construct patterns with (2+1)2 faces, with a = d, b = c.
He can get it on four faces, with two 81 faces, by
U2R2U2R2U2B2R2U2.
I have found a version with a = d on six faces arranged to show (2+1)3.
The pattern is (FU,LU,BU)+ (RU,RB,RD)+ (FR,FD,FL)+ (FLU,LBU)+ (UBR,BDR)+ (FRD,FDL)+ which
is in Swap-Flip. Exercises. Is there any achievable (2+1)3? Is there any
constructible (2+1)3 with b = c (and a = d)? The name of this face pattern
derives from its being a geometric representation of (2+1)2 = 2·2 +
2·1 + 1·2 + 1·1. In N51/52, I discussed planar versions of the Magic Cube. During my recent visit to
Budapest, Tibor Szentiványi gave me a Magic Disc which is a different kind of planar
magic cube. It comprises a circular disc divided into two halves (A and B) surrounded by a
ring of 6 pieces (1 to 6). The outer ring rotates with respect to the inner ring. Further,
when aligned as shown, the right half of the disc can be turned over, exposing the reverse
sides B', 1', 2', 3' as shown. The two sides have pictures of dogs in blue and brown and
they are not easy to keep track of. If we hold it with A up, there are only 1152 distinct
patterns and these readily reduce to 96. I find the diameter of the reduced Cayley graph
is 7 and there are nine antipodes. Despite the simplicity of the problem, it is not trivial
to produce an algorithm nor to determine just what patterns are possible. If the outer ring
of the disc has only 4 parts, then there are 48 patterns which reduce to 6, where the
Cayley graph is a 6-cycle. The case with 2n parts, for n≠3, is quite different to the 6
part case.
In N51/52, I discussed planar versions of the Magic Cube. During my recent visit to
Budapest, Tibor Szentiványi gave me a Magic Disc which is a different kind of planar
magic cube. It comprises a circular disc divided into two halves (A and B) surrounded by a
ring of 6 pieces (1 to 6). The outer ring rotates with respect to the inner ring. Further,
when aligned as shown, the right half of the disc can be turned over, exposing the reverse
sides B', 1', 2', 3' as shown. The two sides have pictures of dogs in blue and brown and
they are not easy to keep track of. If we hold it with A up, there are only 1152 distinct
patterns and these readily reduce to 96. I find the diameter of the reduced Cayley graph
is 7 and there are nine antipodes. Despite the simplicity of the problem, it is not trivial
to produce an algorithm nor to determine just what patterns are possible. If the outer ring
of the disc has only 4 parts, then there are 48 patterns which reduce to 6, where the
Cayley graph is a 6-cycle. The case with 2n parts, for n≠3, is quite different to the 6
part case.