CUBIC CIRCULAR
A quarterly newsletter for Rubik Cube addicts
Issues 7 & 8
Summer 1985
THE LAST CUBIC CIRCULAR - SPECIAL TRIPLE SIZE ISSUE
CONTENTS
| page | | |
| 2 | | Editor's Corner, Oxford Series in Recreational Mathematics |
| 3 | | Sources in Recreational Mathematics. Centre for Mathematical Recreations and Puzzles. Puzzling Announcements. |
| 4 | | New Cube Products. |
| 6 | | Rainbow Patterns. |
| 7 | | Shepherd's Bloody Cube. |
| 8 | | More on the U Group. More on Local Maxima. Some Pretty Random Patterns. |
| 9 | | Some Comments about the 43. A 34 Simulator. |
| 10 | | The Theory of the n3. |
| 12 | | The 53. |
| 13 | | Rubik's Mate - The Siamese Cubes. |
| 14 | | Geometry of the 63 and 73. |
| 15 | | The Skewb or Pyraminx Cube. |
| 18 | | God's Algorithm for the Pyraminx, |
| 19 | | Uriblock. More on the Hungarian Rings. |
| 20 | | Some Notes on Polyhedra. |
| 24 | | Regular Polyhedra, |
| 25 | | Kepler-Poinsot Polyhedra. |
| 26 | | Honeycombs. |
| 27 | | Semi-regular Polyhedra. |
| 28 | | Archimedean Polyhedra. |
| 30 | | Archimedean Tessellations. |
| 31 | | Uniform Polyhedra. Regular-faced Polyhedra. |
| 32 | | Tessellations and Tilings. |
| 34 | | Addendum. |
| 35 | | Sliding Cube Puzzles. |
| 36 | | A Rubric on Rubik Cubics. By Claude Shannon. |
| 39 | | The XL-25. |
| 43 | | Curious Cubic Correspondence. |
| 45 | | A 43 Competition. 1000DM in Prizes. A Cubic Sick Joke. |
| 46 | | Rubik's Foundation. Youngest Cubist? Cubic Mail Box. Rubik Cubik Magik. A Novel Appearance. |
| 47 | | The History and Further Trials of the Cube. A Rumour. |
| 48 | | Some Pyraminx Variations. A Mad Comment. |
Published by David Singmaster, 87 Rodenhurst Road, London, SW4 8AF, UK.
ISSN No, 0261-8362, All material © 1985 by David Singmaster.
2
EDITOR'S CORNER
SURPRISE, SURPRISE! I bet you'd all given up on me by now!
I have had numerous letters asking when this would appear. Frankly, I haven't had the foggiest idea most of the time. I feel I owe you all a few words of explanation.
I first started typing sections of this in Autumn 1983, when I prepared the long section on polyhedra for my geometry class. Since then I have been meaning to get around to it every few months. Unfortunately I had a massive overdose of cubism in 1982-83. David Singmaster Ltd. was closed down, and I lost a fair amount of money -more than I had made previously. This led to prolonged tax negotiations. Also I was still receiving more post than I could deal with. Indeed there is still a pile about a foot (30cm) high that I haven't got around to, as well as about 18 inches (45cm) of Xeroxes of articles that I haven't looked at yet. In addition, I was teaching several extra courses in 1983-84, including the geometry course which was being taught for the first time. I also spent a lot of time helping to rewrite a Department submission that had been rejected. I have also started on some other projects which have taken up much of my time. I will describe these below as they should be of interest.
Fortunately, I was promoted to a Readership (= Research Professorship), the first in my Faculty, as of September 1984 and this is giving me more time to get caught up. I have worked in spurts over the past year - some of you will have had answers to letters from 1983! I have spent this summer working very hard at getting caught up. I have nearly read all my unread back journals and have nearly got through all the unanswered letters on my desk, etc. If you haven't yet had an answer, hold on!
In a week, I am going to City College of New York for the Autumn term. I will not have completed answering all my post by then, but I'll probably do some more before then. If you haven't had an answer by about the time you get this, I will get to your letter when I return in January. Meanwhile, my apologies for the delay or non-response to your letters and the delay in compiling this Circular.
THE FUTURE. I don't plan to produce any more Circulars. However, I will eventually prepare an Index and I have a bibliography on the Cube which requires considerable additions, even though it already runs 70 pages. If and when I get around to producing these, I will circulate the present subscription list and let you know what they will cost. (The bibliography will need several pounds just for postage, unless I reduce and double-side it.)
OXFORD SERIES IN RECREATIONAL MATHEMATICS
Anthony Watkinson, mathematics editor at Oxford University Press, asked me to edit a series in recreational mathematics. (Anthony was formerly with Academic Press, where he edited 'Winning Ways'.) We have embarked on this series. One book was already in hand and put into the series. Another has just appeared, two are ready to go into production and several others are being written. The first books in the series are the following.
Hugh ApSimon. Mathematical Byways in Ayling, Beeling and Ceiling. October, 1984. This is a collection of simple but difficult problems, e.g. find the smallest rectangle of wrapping paper required to cover a box.
3
John Beasley. The Ins and Outs of Peg Solitaire. August, 1985. This is the first book on the subject in nearly a century and will be the standard work for about that long!
Ernő Rubik, et al. Rubik's Cubic Compendium. Spring, 1986? This is the book mentioned in C1-4 and C2-3. I have just finished an additional chapter summarising the later history of the Cube. (Title not yet fixed.)
Edward Hordern. Sliding Piece Puzzles. Summer, 1986? This will describe some 250 puzzles of this type which began with Loyd's 15 Puzzle. (Title not yet fixed.)
We are hoping to produce a translation of Wilhelm Ahrens' 'Mathematische Unterhaltungen und Spiele' (1910-1918), which is the most scholarly of all books on recreational mathematics and extremely difficult to obtain.
Sources in Recreational Mathematics - see below for a discussion of this project.
The above gives some indication of the kind of books we are looking for. If you have any suggestions, please write to me.
SOURCES IN RECREATIONAL MATHEMATICS
As a possible took for my series, I started to compile original sources of classical recreational problems. It has become apparent that the first step is to prepare an annotated bibliography of the source material. I have begun doing so and have put it on a computer file. It is now 95 pages long, with about 200 subjects with information listed chronologically for each subject. I have also found a good many problems and have compiled a 17 page file of queries and problems on this material. I also have a draft article which outlines the project and some of the material. I would be delighted to hear from anyone interested in this project.
CENTRE FOR MATHEMATICAL RECREATIONS AND PUZZLES
A few years ago, I thought that a puzzle museum ought to exist. I had some general ideas on this and then I discovered that Ivan Moscovich, the well known Israeli puzzle inventor, had been the founder of the Israeli Museum of Science and Technology and was interested in a puzzle museum also. We have been discussing this now for two years. I wrote out a preliminary version of our ideas in Spring 1984, but I have not yet had time to pursue it vigorously.
PUZZLING ANNOUNCEMENTS
An exhibition based on Jerry Slocum's puzzle collection will be at the Los Angeles Craft and Folk Art Museum from 20 Nov 1985 to 30 Jan 1986. I believe it will then travel to New York.
If you are interested in wooden puzzles, then you are probably familiar with Stewart T. Coffin's puzzles. In fact, many of them have also been made in plastic by firms such as Mag-Nif, Tenyo and the Museum of Modern Art. He has just produced a new edition of his book 'Puzzle-Craft'. This is 100 pages of how to make his puzzles in wood. It costs only $12. Write to him at 79 Old Sudbury Road, Lincoln, Massachusetts, 01773, USA. If you live outside the USA and Canada, I'd suggest adding a few $ for postage. He will only accept $ money orders, $ cheques drawn on a New York bank or $ cash.
There are only two distributors/retailers that I know of who are puzzle specialists.
Rainer Bathke, Village Games, 53A Court Nope Road, London, NW3, UK.
Dietmar Hartung, Arndtstr. 13, 0-1000 Berlin 61, Germany.
(Bathke has a weekend shop at Camden Lock in London.)
4
There are two especially active cubists.
Christoph Bandelow, Haarholzer Str. 13, D-46314 Bochum-Stiepel, Germany. Bandelow is the author of 'Einführung in die Cubologie', Vieweg, Braunschweig, 1981 (C3/4-26). This was expanded into English as 'Inside Rubik's Cube and Beyond' , Birkhäuser, Boston, 1982. It is one of the most comprehensive books on the cube.
Georges Helm, 76 Bomecht, L-4936 Bascharage, Luxemburg. Helm is the Rubik's Cube Club of Luxemburg which appears to be the only club still in existence! He has compiled a name index for Circulars 1 - 6.
NEW CUBE PRODUCTS
Cubes for the blind (C1-6) were made commercially in Germany. One type had metal studs, another had 1 to 6 raised spots formed by a hot rod applied to the faces. Bandelow has shown me some with raised molded plastic shapes. Metal studded 23 and 43 were also made.
Bandelow says cubes with pastel colours are being made in China, but I don't recall that he had one. He did however give me a solution book in Chinese!
Wim Osterholt has kindly sent a number of registered designs from Germany. Gerhard Josten, no. 81 03 943, published 25 Jun 1981, has an icosahedral puzzle, of the same concept as the Impossi-ball, but with the supporting pillars reaching outside to give a knobby appearance. Walter Moll, 81 04 382, 30 Jul 1981, is the earliest design for the magic dodecahedron, preceding the Hungarian application by a few weeks. Gerhard Josten, 81 06 197, 10 Sep 1981, shows an icosidodecahedron! Gebrüder Obermaier, 81 08 498, 24 Sep 1981, shows a 53, Toni Obermaier kindly sent me the drawings for this. It is a quite different mechanism from Udo Krell's version that Mèffert has produced. Obermaier's is all tongue and groove. Franz-Josef Decker, 81 11 356, 26 Nov 1981, is a general magic polyhedron.
I have recently seen Calendar Cubes (C1-5, C3/4-8) from Italy and Japan. The Japanese is essentially an English language Calendar Cube simplified so that there is room to put pictures of some pop star on the other facelets.
 When I was in Poland in 1983, I accidentally found a shop with four shapes of cube that I have never seen elsewhere. These were labelled Original Toys, Poland. The first was the twisted octagonal prism shown on the right. This has two areas interlocked like the halves of a tennis ball or baseball. These two areas are solidly coloured giving a peculiar two-coloured object. I have shaded one of the areas in the figure.
When I was in Poland in 1983, I accidentally found a shop with four shapes of cube that I have never seen elsewhere. These were labelled Original Toys, Poland. The first was the twisted octagonal prism shown on the right. This has two areas interlocked like the halves of a tennis ball or baseball. These two areas are solidly coloured giving a peculiar two-coloured object. I have shaded one of the areas in the figure.
The second Polish Cube was a pointed 'cushion'. Consider the 'cushion' shown at C1-9. Put square pyramids on the top and bottom face centres, so the eloping sides come up to a point. This is four-coloured in four segments going from the top to the bottom. A colour covers an upper and a lower sloping triangle and the middle row in between.
The rhombic dodecahedron is the dual of the cube-octahedron. It has been described at C5/6-13, but I give a figure on the next page.
5
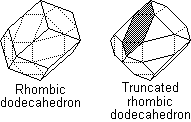 It has twelve rhombic faces whose acute angles meet at four fold vertices and whose obtuse angles meet at three fold vertices. The rhombuses correspond to the edges of a cube or octahedron, The rhombic dodecahedron is the shape obtained by trimming a cube to octagonal cross sections along all three axes, then peaking all the face centres to square pyramids. Alternatively, if you take a geometric cube and cut it by 45° planes along all edges, the result is the rhombic dodecahedron. The third Polish Cube was a proper rhombic dodecahedron, with 12 colours. I find this a most elegant shape. It is actually equivalent to Mondadori's Master Cube (C3/4-9) but the structure is clearer on the Polish version.
It has twelve rhombic faces whose acute angles meet at four fold vertices and whose obtuse angles meet at three fold vertices. The rhombuses correspond to the edges of a cube or octahedron, The rhombic dodecahedron is the shape obtained by trimming a cube to octagonal cross sections along all three axes, then peaking all the face centres to square pyramids. Alternatively, if you take a geometric cube and cut it by 45° planes along all edges, the result is the rhombic dodecahedron. The third Polish Cube was a proper rhombic dodecahedron, with 12 colours. I find this a most elegant shape. It is actually equivalent to Mondadori's Master Cube (C3/4-9) but the structure is clearer on the Polish version.
The fourth unique Polish Cube was a truncation of the rhombic dodecahedron. Since the rhombic dodecahedron has two types of vertices, there are three kinds of truncation - at the four fold vertices, at the three fold vertices and at both. The first gives the truncated rhombic dodecahedron described at C3/4-11 and C5/6-5, which is twelve-coloured. The kind gives the Polish truncated rhombic dodecahedron. This was strangely six-coloured. Looking at the figure above, you can see three orthogonal great-circular bands on the solid. I have shaded one of the four regions that form such a band. In the Polish object, two of these bands were solidly coloured and the other four regions were joined with the triangles and given four colours. The third kind of truncation of the rhombic dodecahedron gives the small rhombi-cuboctahedron (C1-9) and these were also available in Poland, but are also widely available elsewhere.
 The East German firm VEB Spielvaren, in Pfaffschwende, is currently producing a series of four variations on the 23. The simplest is just an octahedron formed by truncating the corners of the 23, Each face has three coloured spots, one at each corner, so this is really the same as the six-colouring of the cube. If one puts regular tetrahedra on all eight faces of the octahedron, the result is the Stella Octangula discovered by Kepler. One can view it as two large interpenetrating tetrahedra or as one large tetrahedron with small tetrahedra on the centre of each face. It is four coloured in accordance with this last description - a large face and the small tetrahedron on it are of one colour,
The East German firm VEB Spielvaren, in Pfaffschwende, is currently producing a series of four variations on the 23. The simplest is just an octahedron formed by truncating the corners of the 23, Each face has three coloured spots, one at each corner, so this is really the same as the six-colouring of the cube. If one puts regular tetrahedra on all eight faces of the octahedron, the result is the Stella Octangula discovered by Kepler. One can view it as two large interpenetrating tetrahedra or as one large tetrahedron with small tetrahedra on the centre of each face. It is four coloured in accordance with this last description - a large face and the small tetrahedron on it are of one colour,
If one puts tetrahedra on just four of the faces of the octahedron, the result is a large tetrahedron which rotates on its midplanes. These are the plane which bisect four of the edges of the tetrahedron cutting the tetrahedron in a square cross-section. The tetrahedron is naturally four-coloured. It changes shape as it turns giving rise to some seven different shapes. These correspond to the seven different patterns on the 23 of Obermaier described on C3/4-9.
6
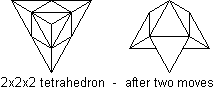 This 2 × 2 × 2 tetrahedron was invented by several people, including Rubik and Barry Lockwood of Rochdale.
This 2 × 2 × 2 tetrahedron was invented by several people, including Rubik and Barry Lockwood of Rochdale.
The last of the East German versions is again a simple idea. Start with an ordinary 2 × 2 × 2 cube and trim four parallel edges to leave a square prism. This also changes shape as it turns. It comes with just two colours - four pieces are solidly red and four are solidly yellow. One of the easy standard shapes is the house shown and the puzzle is called Trick Haus.
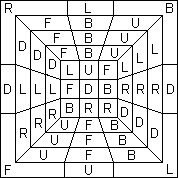 RAINBOW PATTERNS
RAINBOW PATTERNS
Peter J. Kelly sends a 'rainbow' pattern where he gets six parallel stripes of all six colours appearing on two adjacent faces. (We are considering a six-colour rainbow!) I have found the pattern shown, which is an achievable pattern though I found it by construction from a disassembled cube. I haven't found a process for it.
Any two adjacent side faces give a six colour rainbow.
[ try this: D U' B2 D U L' D2 B2 F L2 F2 U2 F' U2 F2 - J ]
7
SHEPHERD'S BLOODY CUBE
In C1-5, I mentioned that one can make interesting cube variations by removing some of the stickers. Removing just the centres gives a cube which is particularly perplexing. Half the times one tries to restore it in a pattern that has a 4-cycle of the centres, but this is not visible because the centre stickers are missing. However, such a pattern is impossible and one finds that it requires an odd permutation of the edges to complete it. This is done by a slice move which also gives the desired odd permutation of centres.
 A more interesting variant has recently been given to me by Alistair Shepherd. He is a haematologist with the Blood Transfusion Service in Liverpool, which produces a small circular sticker showing two adjacent hearts, He has replaced all the coloured stickers on a cube with these, in such a way that each face has all the stickers oriented in the same way. A view is shown in the adjacent figure, where the direction of the hearts is shown by the arrows. Opposite faces have opposite orientations.
A more interesting variant has recently been given to me by Alistair Shepherd. He is a haematologist with the Blood Transfusion Service in Liverpool, which produces a small circular sticker showing two adjacent hearts, He has replaced all the coloured stickers on a cube with these, in such a way that each face has all the stickers oriented in the same way. A view is shown in the adjacent figure, where the direction of the hearts is shown by the arrows. Opposite faces have opposite orientations.
I find this to be perhaps the subtlest cube variation that I have seen, in that its complexity is much greater than its initial appearance. At first, it looks like an Irish Cube, i.e. one where all configurations look the same, since all the stickers are the same. But then one sees that orientations matter, e.g. an B turn produces the next figure.
I then thought there were eight types of corner cube, but further thoughts and careful inspection show that there are just four types of corner and four types of edge. This is most easily seen since the first figure is symmetric under 120° rotation about the URF corner axis. The 4 corner types contain 1, 3, 3, 1 corners, while the 4 edge types all contain 3 edges. Thus there are (3!)2(3!)4/2 . 32/3 = 69984 ways to move the pieces without changing the appearance. The denominator 2 occurs since both edges and corners must have the same parity of permutation and the 32/3 factor gives the indistinguishable twists of the two unique corners.
Additionally, one can multiply this by 24 movements of the centres, since an odd permutation of the centres can be compensated for by an odd permutation of indistinguishable edges and by twisting centres with a total centres twist of 0. This gives 16 79616 positions of the cube having the same appearance. Dividing this into 24N gives 61802 70243 84000 distinguishable patterns.
The above pattern led me to ask: how many ways can one put 6 arrows on the faces of a cube? A priori, there are 46 = 4096 ways, but each of these can be viewed in 24 ways. Further, some patterns are the same from different points of view. Answering this problem thus requires the use of Burnside's Lemma and I find 192 distinct patterns (or 112 if we also consider reflections as equivalent). Many of these have no symmetry and hence a cube with such a pattern
8
of arrows would be both easier and harder to solve - easier because there are fewer confusions and harder because there are fewer distinct ways to make it look right. Even so, there may be pieces which are indistinguishable. Indeed, there are only 10 distinct ways to put arrows on the stickers of an edge piece, so we will necessarily have some edge pieces looking the same. There are 24 ways of putting arrows on the stickers of a corner piece. This leads us to whole set of problems and possible puzzles which I don't want to go into, but if anyone makes up examples, I'd appreciate examples (and some royalties for Alistair Shepherd).
MORE ON THE U GROUP
John F. Jarvis (C5/6-2), at Bell Labs, Holmdel, New Jersey, 07733, USA, has sent me a copy of his 'A set of processes for generating all single face permutations of Rubik's Cube' which gives an extensive, though not complete, analysis of the U group (N49, C3/4-17,36, C5/6-2). Six patterns still require 19 moves. Georges Helm told me that Anneke Treep, Guus Razoux Schultz and friends had it down to 16 moves, but they may be counting differently. Looking again, I see that Jarvis counts 180° turns as one move, so I don't see how Treep & Schultz could be doing so much better. Perhaps there is some mistake somewhere in my remembrance?? Bandelow says that Jarvis's results have been improved and only two patterns remain at 19 moves.
Jarvis applies the following four transformations to a process to get equivalent processes.
- a) Take the inverse of the process.
- b) Reflect the process in the plane between the R and L faces. This interchanges all R and L symbols and takes the inverse of each turn in the process.
- c) Turn the whole cube by I, U, U2, U3.
- d) Turn the top face by I, U, U2,U3
This gives 2·2·4·4 = 64 equivalent processes in general. If these were always distinct, there would be 62208/64 = 972 different classes of equivalent processes to consider. It is not true that these are always all distinct and hence there are 1212 different classes that must be considered.
MORE ON LOCAL MAXIMA
Douglas Hofstadter has sent a note by Dan Hoey and Jim Saxe which studies local maxima in some detail (C5/6-24). By analysis of the group of symmetries of the cube and its possible subgroups, they identify 71 positions which are local maxima.
SOME PRETTY RANDOM PATTERNS
Cecil Smith sends several pretty random patterns (C3/4-32/33). He has six colours on each face and I believe he has the same pattern on each face, though he asserts this clearly only for the first of the following face patterns.
9
SOME COMMENTS ABOUT THE 43
The eccentric 43 made from a 33 which I described on C5/6-5 is due to Nob Yoshigahara. He also made a 23 into a 33 in the same way.
Alistair Shepherd sends a shortish edge 2-cycle.
(Ll)2BrB'U2Br'B'U2B2r'B2(Ll)2 = (UFr,FUl)(Urb,Dlb,Drf,Fld) (Urf,Dlf,Drb,Flu)
Christoph Bandelow sends the following.
r2UbU'F2Ub'UrU2F2r2 = (UFr,FUI)(Ubr,Fdl,Ufl,Fur)(Ubl,Fdr,Ufr,Ful)
In both cases, the two 14-cycles of centres can be viewed as one 4-cycle of pairs of centres.
Ronald Fletterman, Finkenweg 4, D-3501 Niestetal - 2, Germany, has produced several booklets in English on the 33,43,53, the Siamese cubes and on the <U, R> group. His 43 algorithm proceeds: D centres, edges, corners; d edges; u edges; d centres; u centres; U corners in position, then oriented; U centres; U edges. He gives tables of standard processes, but the simplest process for (UFr,FUl) takes 23 moves and is due to Bandelow.
r2 ·(D2l)2Dl'r'd2lrD'l'r'd2·B2rB2l'B2lB2'·r2 = (UFr,FUl)
His shortest edge swap is for (UFl,BUl) and takes 21 moves.
Rudolf Werz sends a solution doing centres, then edges, then corners. Getting the last edges right without disturbing the centres takes some work. But he has an elegant 3-cycle of edges and of corners.
RrUR'U'R'r'FRF' = (RUB,BUL,UFL)(RUb,BUl,UFl)
This can be viewed as a 3-cycle of corner-edge pairs and all the pieces are in the U face!
After some thinking about C5/6-17, it now seems clear that the number of hand moves in making an axial move LalbrcRd on the 4 is the number of consecutive inequalities in the sequence a, b, 4-c, 4-d. That is, it is the number of internal planes on which turning occurs. Thus L, Ll, L'l'r all take one move; LR, r take two moves; l'r2R takes three moves. This number is not affected by turning the whole cube, so we need only consider the 64 cases where a = 0. Of these, 1 has no hand moves, 9 have 1 hand move, 27 have 2 hand moves and 27 have 3 hand moves. So the number, Sn of positions achievable after n hand moves is at most 18 Sn-1 + 54 Sn-2 + 54 Sn-3 for n > 3. For n <= 3, the sum terminates at S0 (= 1) and the coefficient of S0 is multiplied by 3/2 since there is no previous turn to be on a different axis from. (Cf. N34, C2-8, C5/6-17.) Then the sum Tn = S0 + S1 + ... + Sn is asymptotic to 1.39 (20.73)n. This value first exceeds N = 7.4 × 1045 for n = 35, so God's Algorithm must be at least this long.
A 34 SIMULATOR
William J. Shlaer, 2007 Southeast 96th Court, Vancouver, Washington, 98664, USA, sends a 34 simulator for the IBM-PC with colour monitor. He has an outline algorithm for restoring the 34 which took him several hours and 2757 moves!
10
THE THEORY OF THE n3
Several people have asked me about the n3 and the number of patterns on it. A recent letter from Carsten Butz has led me to the following analysis. It turns out that an extra conservation law comes into play for n > 5.
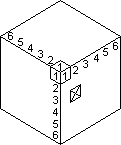 First, one needs further notation. The following is rather ad-hoc for this particular problem and may not be optimal for other problems. We adopt a numerical coordinate system for cubelets. The cubelet (x, y, z) will be in layer x from the R face (so the R face has x = 1), layer y from the F face and layer z from the U face. Then (1, 1, 1) or (111) or 111 denotes the RFU corner which is in the centre of our usual diagram. The case n = 6 is shown on the right with cubelet 111 marked out. I will denote turns as R1, R2, R3, ... meaning to turn the layer x = 1, 2, 3... 90° clockwise as viewed from the R face. Now let a = n+1-a denote the complement of a. Note that 111 is the mirror image of 111 in the midplane of the cube which is parallel to the R face, i.e. the plane given by x = (n+1)/2. On the 33, 111 is LUF.
First, one needs further notation. The following is rather ad-hoc for this particular problem and may not be optimal for other problems. We adopt a numerical coordinate system for cubelets. The cubelet (x, y, z) will be in layer x from the R face (so the R face has x = 1), layer y from the F face and layer z from the U face. Then (1, 1, 1) or (111) or 111 denotes the RFU corner which is in the centre of our usual diagram. The case n = 6 is shown on the right with cubelet 111 marked out. I will denote turns as R1, R2, R3, ... meaning to turn the layer x = 1, 2, 3... 90° clockwise as viewed from the R face. Now let a = n+1-a denote the complement of a. Note that 111 is the mirror image of 111 in the midplane of the cube which is parallel to the R face, i.e. the plane given by x = (n+1)/2. On the 33, 111 is LUF.
Consider now the cubelet 123, whose R facelet is marked with X in the diagram. This can be moved by the turns R1, F2, and U3. Examining the effects of these, we see that
R1 : 123 -> 132 -> 123 -> 132 -> 123 ...; F2: 123 -> 321 -> 123 -> 321 -> 123 ...;
U3: 123 -> 213 -> 123 -> 213 -> 123 ...
We see that any 90° turn gives an interchange of the two values corresponding to the other two directions and a complementation of the value corresponding to the next direction. E.g.
F is a turn in the plane y = 2, so the values in the x and z components are interchanged and the value in the z component is complemented. This leads to a new
CONSERVATION LAW. A piece abc can be moved to a position a'b'c' if and only if a'b'c' is a permutation of abc or of abc or ... or of abc and the parity of this permutation is the same as the parity of the number of complementations.
The argument above established the 'only if' part of this law. The 'if' part is readily seen as it is easy to move the piece onto any face and then into any of the four possible positions on that face. The law shows that a piece can only move to 24 positions at most, while one might have expected 48 positions for a piece like 123. But the law prevents 123 from moving to 132. In fact, a given facelet can move to exactly 24 positions, but for a corner facelet, these lie on just 8 pieces, while for edges and centres, these lie on 24 distinct pieces. (See later.) This phenomenon does not appear on the smaller n because they do not have a centre piece which is asymmetric in the way that 123 is. However Chris Rowley points out that a simpler form of this phenomenon already appears on the 3 and the 4 if one marks them unsymmetrically as indicated on the next page. Each face is given the same appearance, and then the asymmetrical pattern is preserved by any movement of the faces. In fact, this is the principle of White's Irish Cube (C3/4-10) and of the fact that one cannot flip an edge in place on the 43.
Now we can determine the number of patterns on the n For convenience, we begin with the even case: n = 2m. Then we have the following types of pieces.
11
 |
 |
| Patterns showing asymmetric conservation |
| Corners: | 1 type of 8 pieces. |
| Edges: | m-1 types of 24 pieces. |
| Centres: | (2m-2)2/4 =(m-1)2 types of 24 pieces. (Of these, m-1 types are diagonal and the others are non-diagonal.) |
A priori, the corners have 8!·38 arrangements and the other pieces have (24!)m-1·(24!)(m-1)² = (24!)m²-m arrangements. (Here, we have used the fact, discovered on the 43, that edge orientation is determined by position. I.e. we do not have a factor analogous to the 212 which appears on the 33.) We can easily see that we can divide by factors of 3 (conservation of total corner twist), of 24 (direct symmetries of the cube) and of (4!)6(m-2)² (rearrangements within the 6(m-1)2 groups of 4 indistinguishable centres - if we have solidly coloured faces). But we must examine parity conservation rules to see if there are further divisors.
Consider any 90° turn of an outer layer, e.g. B1. This gives a 4-cycle of corners, a pair of 4-cycles on each type of edge and a 4-cycle on each type of centre. Any turn of an inner layer gives a 4-cycle on one type of edge, a pair of 4-cycles on one type of diagonal centre and a 4-cycle on each of 2m-4 types of non-diagonal centre. From this, we see that all types of diagonal centre must have the same parity as the corners, while all types of non-diagonal centre must have the same parity as the total of the corner parity and all the edge parities. Hence all the (m-1)2 types of centre have their parity determined by the corners and edges. Further since we can readily form 3-cycles of each type of piece, twist two corners and adjust the parities of the corners and edges, we see that we have 8!·38·(24!)m²-m / 3·24·2(m-1)² achievable patterns when the centre pieces are distinguishable. If the faces are solidly coloured, then our divisor of (4!)6(m-1)² must also be divided by 2(m-1)² since each of the (m-1)2 types of 24 centres can be rearranged only in half of the (4!)6 ways which preserve the colouring. Thus there are 8!·38·(24!)m²-m / 3·24·(4!)6(m-1)² achievable patterns when the faces are solidly coloured. For m = 3, n = 6, the first number is 1.31 × 10148 and the second number is 1.57 × 10116 (I have computed these in full, but I don't think anyone except me is sufficiently interested in them.)
Now we consider the odd case: n = 2m + 1. This gives us an extra type of edge consisting of just 12 pieces. (On the previous page, I see I said that an edge facelet could move to 24 facelets, lying on 24 distinct pieces. This fails here - when n is odd, there is one type of edge facelet whose 24 equivalents lie on just 12 distinct pieces.) We also have m-1 extra types of centre having 24 pieces (which we will call central centres) and 6 extra Centres, which we will assume to remain fixed. Our a priori number is now 8!·38·(24!)m-1·12!·212·(24!)(m-1)²·(24!)m-1·46, where the 46 corresponds to turning Centres.
12
A 90° turn of an outer layer gives a 4-cycle of corners, a pair of 4-cycles on each type of non-central edge, a 4-cycle on central edges, a 4-cycle on each type of centre except the Centre and a 90° turn of a Centre. Any 90° turn of an inner layer (excluding the central layer since we are keeping the Centres fixed) gives a 4-cycle on one type of non-central edge, a pair of 4-cycles on one type of diagonal centre and a 4-cycle on 2m-3 types of types of non-diagonal centres. From this, we see that the following types must be in the same parity as the corners:
the central edges; all m-1 types of diagonal centres; the number of 90° turns of Centres. All the (m-1)2 types of non-diagonal centres have the same parity as the sum of the parities of the corners and non-central edges.
So far, this gives divisors of 2, 2, 2m-1 and 2(m-1)². We also have the usual divisors of 3 and 2 to allow for the conservation of the total twist of corners and edges. Again it is easy to find 3-cycles of each type of piece, twist two corners or edges and adjust parities of corners and edges. So there are 8!·38·(24!)m²-1 ·12!·212·46/3·2·2·2·2m²-m achievable patterns when all the centres and Centres are distinguishable (including rotation of the Centres). If the faces are solidly coloured, we can divide this by (4!)6(m²-m)·46/2m²-m·2. This gives us 8!·38·(24!)m²-1·12!·212 / 3·2·2·(4!)6(m²-m) achievable patterns when the faces are solidly coloured. For m = 3, 2m + 1 = 7, the first number is 3.04 × 10211 and the second number is 1.95 × 10160 (Again, I have computed these in full.)
You may like to verify that the formulae are correct for n = 2, 3, 4 and 5. The formulae for solidly coloured faces agree with those sent by Butz.
Christoph Bandelow and Rudolf Werz have both obtained the same results.
THE 53
Several designs for the 53 were proposed. The design of Udo Krell, of Hamburg, was produced by Mèffert in Hong Kong. This was marketed in 1983 in Germany as "Rubik's Wahn" (Wahn = delusion or illusion) at about 40DM and in Japan. It is 70mm (2 3/4 in) on an edge and weighs 290g (10 1/2 oz). It moves remarkably well. The mechanism is a 33 whose pieces have grown out to the boundary of the 53 space and then the extra pieces are fitted in between. It is not recommended to take it apart - I managed to do so and was then quite uncertain whether I would ever get it back together. The pieces have quite small parts yet I have not heard of any breaking. I have seen one of the diagonal centre pieces get twisted. The main problem I have found is that the stickers are a bit small and hence easily come off. If one puts the 53 loose into a bag of papers, etc., one discovers a sticker has come off somewhere and has to search every bit of paper to find the missing sticker Hence I now keep it in its own plastic bag. The solution of the 53 is actually no more complex than for the 43, as can be seen from the preceding discussion. It just takes much longer. However, one must take greater care in keeping the cube squared up and this may be slowing one down more than just the greater number of moves. I think that racing the 53 is likely to be a bit hazardous to the pieces.
Although the 53 presents no new problems for solution, there are some nice patterns which can be obtained on it and which cannot be obtained on the 43, e.g. six chessboards or 6-x patterns.
Christoph Bandelow has recently bought the remainder of the German 53 stock and you can buy examples from him.
13
RUBIK'S MATE - THE SIAMESE CUBES
In C3/4-12, I described the Siamese Cubes devised by Tony Fisher. In 1983, Ideal produced this same idea as Rubik's Mate. Initially one hopes that the pieces can move from one cube to another, but a little contemplation shows that each part is separate from the other and that each half behaves like an ordinary 33 with the three pieces along one edge held together. One can easily simulate this by using some heavy tape along an edge. I will refer to this as the rigid edge. Below I analyse the group and describe some methods of solving such a cube.
ANALYSIS
1) One easily determines where the rigid edge belongs. On Rubik's Mate, you cannot see the edge piece in the middle of the rigid edge, so one must use elimination. The ends of the rigid edge are visible and determine its orientation. It is then easy to put the rigid edge in place correctly.
2) The four edges adjacent to the rigid edge can be readily put in place correctly.
3) At this point, we have a correct 2 × 2 × 3 block along the rigid edge. If we hold the cube with the rigid edge as the LB edge, we have only the pieces in the F and B faces to consider. In my discussion of the group <F,R> (N55/57), it is shown that <F,R> contains all permutations of these edge pieces, so we can get all the edges in place using just F and R moves.
4) However, we actually have more moves available. If we hold the cube so the rigid edge is FD, then the first flip in Section 5.8.A (iii) of my Notes (N44), namely a+b+ (= UB+UR+) = B'U2B2UB'U'B'U2FRBR'F', can be applied to flip two edges. Since part 3) above shows that the edges can be moved arbitrarily, it follows that we can flip any even number of edges.
5) Now consider the corners. If we hold the rigid edge as LB, then we can only turn F, R, B, L. As far as the corners are concerned, B is the same as F and L is the same as R. So any sequence of turns of our cube has the same effect on edges as a sequence of F and B turns where F and R are defined with respect to the rigid edge at LB. We know that the action of <F,R> on corners is isomorphic to S5 which has 5! = 120 patterns, half of which are even. We also know that we can obtain the even patterns by use of just F and R moves. Further, we know that we can obtain any permissible twisting by use of F and R moves.
Hence, if the rigid edge is in place, we have
N1 = 11! 5!/2 · 36/3 · 211/2 = N/(12·8·7·6·32·2) = 59595 46306 56000 patterns. (Here N is the number on the normal cube (N12).) If we let the rigid edge take up any of its possible 24 places, then we have
N2 = 24 N1 = N/(8·7·6·32) = 14 30291 11357 414000 positions.
On Rubik's Mate, we have two independent parts, each having this many patterns, so there are
N22 = 204 57326 69569 89719 99443 35360 00000 patterns on the whole thing.
This analysis shows that my question on C3/4-12: can a cube with a column correctly lined up be restored without breaking up the column? is answered: no. For the 6 other corners can be in any one of the six cosets of the action of <F,R> and only one of these cosets can be restored. Thus, if we scramble the cube at random, line up one column and then rigidify it, we have only a 1/6 chance of being able to restore it. This shows up in the 6 occurring in the denominator of N - the rest of the denominator corresponds to fixing two corners by an edge in a column, but the 6 is an extra factor.
14
Having determined the group, it is possible to solve the problem in many other ways. Though I haven't tried it often, I think the following strategy may be easier.
1) & 2) as above.
3) Place corners 1 and 2 correctly (where the corner numbering is in Figure 5.10, p. 56 of my Notes). Then the remaining corners can be put in position by turning R.
4) Orient the corners. Since edges are not important yet, we can use simpler moves than those on N57. Recall that P3 = P22 = [F, R]2 = FRF'R'FRF'R'. Then the following are useful:
(P3R)3R2 = 5-6+;
(P3R')3R2 = 3-4+;
[P3, R] = 3+4+6+;
[P3, R'] = 3-5-6-.
5) Move edges into place. The Varga-Fried move and my P1 (= F2R2)3 can both be used in many conjugates, but not all conjugations are easily accomplished. One can also form the commutator of P2 = [F, R] with the slice RRs': [P2, RRS'] = (UR, FD, RD). This can be used to get a 3-cycle in the R face simply by conjugating with F. This 3-cycle does not preserve orientations of pieces so skilful use of it can correct orientations while placing edges.
6) If necessary, flip edges by the method of 4) in the first method.
GEOMETRY OF THE 63 and 73
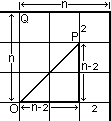 Now that a 53 has been made, people often ask about 63, etc. I was told that these were impossible as the corners would fall off as face turned. However, upon checking, this does not actually happen until n = 7, If we assume the cubies have edge 2, then the distance from the face-centre O to the edge of the cube is n and the distance from O to the inner corner P of a corner piece is x = (n-2)√2. So the corner will fall off as it turns if x > n, i.e. (n-2)√2 > n. This easily gives n > 2√2/(√2 - 1) = 4 + 2√2 = 6.8+. So a 63 is technically possible with cubical cubies, but a 73 is not. One can get around this by making the outer layers thicker than the inner layers, as with Trajber's octahedron (C1-7/8), but I don't know that anyone has done it.
Now that a 53 has been made, people often ask about 63, etc. I was told that these were impossible as the corners would fall off as face turned. However, upon checking, this does not actually happen until n = 7, If we assume the cubies have edge 2, then the distance from the face-centre O to the edge of the cube is n and the distance from O to the inner corner P of a corner piece is x = (n-2)√2. So the corner will fall off as it turns if x > n, i.e. (n-2)√2 > n. This easily gives n > 2√2/(√2 - 1) = 4 + 2√2 = 6.8+. So a 63 is technically possible with cubical cubies, but a 73 is not. One can get around this by making the outer layers thicker than the inner layers, as with Trajber's octahedron (C1-7/8), but I don't know that anyone has done it.
The amount of overlap left as the face turns is the difference n - x. Simple computation of (n-x)/2√2 gives a measure of how much of the cubie diagonal remains on the face. The values of this ratio are given below.
| n= |
2 |
3 |
4 |
5 |
6 |
7 |
| (n-x)/2√2 = |
.707 |
.561 |
.414 |
.268 |
.121 |
-.025 |
So we see that the 63 overlaps by only about 1/8 of its diagonal. This seems too small for practicality since the pieces at the edge of the face must have some thickness.
15
THE SKEWB OR PYRAMINX CUBE
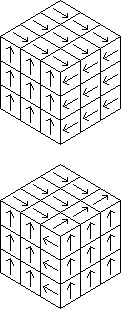
I described this in C3/4-12/13. It has been discussed by Douglas Hofstadter in Scientific American, July 1982, and he suggested the name Skewb. Mèffert has produced the moulds for it and has made up small numbers of it. I find it very intriguing. My analysis now confirms Tony Durham's number of patterns given on C3/4-13.
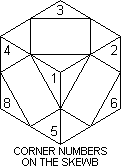 As usual, we first need some notation. We refer to the eight corners as URF, etc. and the six centres as U, R, F, D, L, B. Since a move is most easily described as the turning of a corner, it is convenient to have simple names for the corners. I use the numbers 1 to 8 as shown in the adjacent figure. (Corner 7 is the hidden LDB corner.) Then the move 1 means the turn of the half cube centred on corner 1 by 120° clockwise, as viewed from the outside. I also use 1+, 1- for the action of a move when corner 1 is rotated in its place.
As usual, we first need some notation. We refer to the eight corners as URF, etc. and the six centres as U, R, F, D, L, B. Since a move is most easily described as the turning of a corner, it is convenient to have simple names for the corners. I use the numbers 1 to 8 as shown in the adjacent figure. (Corner 7 is the hidden LDB corner.) Then the move 1 means the turn of the half cube centred on corner 1 by 120° clockwise, as viewed from the outside. I also use 1+, 1- for the action of a move when corner 1 is rotated in its place.
Now we note that the 8 corners form two tetrads. 1,3,6,8 and 2,4,5,7. It is not possible to move a corner from one tetrad to the other. Further, each move is a 3-cycle on one tetrad and a twist on the other. If we only turn corners in tetrad 1,3,6,8, then this tetrad remains fixed in space - its only movement is possible twisting of its corners in their places. Then this tetrad determines the Skewb's spatial orientation and we can recover the spatial orientation from the pattern on the Skewb, Caution. If we mix turns from both tetrads, then the pattern does not determine the spatial orientation. There are 12 rigid motions of the Skewb which rearrange tetrad 1,3,6,8 and there are 24 such motions if we allow the tetrads to be interchanged - but we usually don't. Some patterns are easier to describe after reorienting the Skewb and I will use R, U, for turns of the whole Skewb (C3/4-26). A pleasant example was shown to me by Mèffert: 143214321R'U = (F, L, B, U) (R, D). Note that each 90° turn of the whole Skewb interchanges its tetrads.
Let us explore some basic moves. If we are looking at just two corners, there are only two useful cases. 1,2 and 1,3. Their commutators are as follows.
| | | moves |
| 1. | [1, 2] | = 4+1+2-6- (F, U) (R, B) | (4) |
| 2. | [1, 2]2 | = 4-1-2+6+ | (8) |
| 3. | [1, 2]3 | = (F, U) (R, B) | (12) |
|
| 4. | [1, 2']3 | = (F, B) (R, U) | (12) |
|
| 5. | [1', 2']3 | = (F, R) (U, B) | (12) |
|
| 6. | [1, 3] | = (LUF, FRD)+ (UBR, BLD)- (U, B, F) | (4) |
| 7. | [1, 3]2 | = 4+5+2-7- | (8) |
| 8. | [1, 3]3 | = (FLU, FRD) (BRU, BLD) | (12) |
16
These are already a rich set of moves - we have a pair of corner 2-cycles, a 4-twist and several pairs of centre 2-cycles. It is not hard to see that these are already sufficient to restore the Skewb, but restoration is much easier if we find a few more moves first.
| 9. | [1, 3][6, 8] | = (F, U, D) | (8) |
| 10. | 1.[1, 3][6, 8]·1' | = (R, F, D) | (9) |
| 11. | 6'·[1, 2]3·6 | = (U, F) (B, D) | (14) |
|
| 12. | 5·[1, 2]3·5' | = (U, D) (F, B) | (14) |
|
| 13. | 143214321R'U | = (F, L, B, U) (R, D) | (9) |
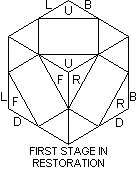 To restore the Skewb, we can proceed as follows.
To restore the Skewb, we can proceed as follows.
Stage 1. Select a tetrad and twist its corners so the tetrad is correct, e.g. as shown in the figure.
Stage 2. We need a:
Theorem. If the tetrad 1, 3, 6, 8 is correct, then the tetrad 2,4,5,7 is either correct or in a pair of 2-cycles.
Proof. The group of rigid motions of the tetrad 2,4,5,7 is A4, the group of even permutations of four elements. This is easily seen to be generated by the 3-cycles (2,5,4), (2,4,7), (2,7,5) and (4,5,7), corresponding to the clockwise corner turns 1, 3, 6, 8, respectively. (Cf. N10.) Let T denote the total number of clockwise corner turns in achieving a particular permutation of the tetrad 2,4,5,7. E.g. 16'132 would have T = 1 - 1 + 1 + 2 = 3. Since the cube of a turn is the identity, we must consider T (mod 3) and we call this the twist of the permutation. Note that this is both the number of 3-cycles used to form the permutation and the sum of the twists of the corners in 1,3,6,8. Direct calculation verifies that the product of two permutations has the sum of their twists. In group theory, we say that the mapping from permutations to twists is a homomorphism from A4 onto Z3. Now if 1,3,6,8 is correct, then its corners have no twist, so the permutation of 2,4,5,7 must be a product of T 3-cycles, where T is 0 (mod 3). The only such permutations are then checked to be I and the three pairs of 2-cycles.
This proof is really too computational to be enlightening. The subgroup where T is 0 (mod 3) is isomorphic to Z22 (N59) and is called the Klein-4-group. It is the smallest non-cyclic group and is the group of symmetries of a rectangle, hence is a subgroup of the symmetries of a square. I have not seen the above geometric description of Z2 in A4 before though it is well known that Z22 is an important subgroup of A4. (Indeed it is the only normal subgroup and its presence is why it is possible to solve an equation of the fourth degree by radicals.) One can get a more geometric perspective on this result by considering the three edge to edge axes of a tetrahedron. (These are the face to face axes of the Skewb if one takes a tetrad as our tetrahedron.) These axes are permuted among themselves by A4 acting on the tetrahedron.
17
Assuming that our axes are directed, so that we can see which end is which, A4 can reverse some of the axes in place. The actions which leave the axes in place, though possibly inverted, form our subgroup Z22. The amount of twist T corresponds to the amount of cyclic rotation of the three axes. We can only reverse 0 or 2 since even permutations of our tetrad correspond to even permutations of our six axis ends. In fact, this description of A4 is the same as the group of centres on Rubik's Cube (N46/47). Our subgroup Z2 corresponds to the three 4-spot patterns and I.
However we see our Theorem, it immediately implies that we can turn the Skewb so that formula 6 above will put the second tetrad in place.
Stage 3. From the proof of our Theorem, we see that the total twist of the corners in 2, 4, 5, 7 must be the same as the number of 3-cycles in the permutation of 1, 3, 6, 8. But 1, 3, 6, 8 has been put right, so then the total twist of 2, 4, 5, 7 must be 0 (mod 3).
We now have four cases. In each case, all the possible arrangements are equivalent by movements of the whole cube.
Case 1. No twists needed - do nothing.
Case 2. Two twists required, one + and one -.
| 14. | [[1, 2], 6] | = 2-5+ (R, B, D) | (10) |
Case 3. Three twists required, all the same.
| 15. | (13)3 | = 2-5-7- (U, L, R, B, F) | (6) |
Case 4. Four twists required, two + and two -. Use formula 7 of the list above.
Stage 4, We now have only to put the centres right and these are in an even permutation since any corner turn or any movement of the whole Skewb has the same parity of corner permutation as of centre permutation. It is not hard to see that formula 3 on our list is sufficient to restore the centres, but formulae 5, 6 and 9-13 greatly simplify the process.
Case 1. Any 3-cycle can be done in <=9 moves by use of 9 and 10.
Case 2. Any pair of 2-cycles can be done in <=14 moves by 3, 4, 5, 11, 12.
Case 3. Any 5-cycle (A, B, C, D, E) is a product of two 3-cycles (A, B, C)(A, D, E), so it can be done in <=18 moves by two uses of case 1.
Case 4. Any (4-cycle and 2-cycle) can be done in <=13 moves by conjugating formula 13 by at most two moves.
Case 5. Any pair of 3-cycles can be done in <=18 moves by two uses of case 1.
Thus we can always restore the Skewb in at most 4 + 14 + 10 + 18 = 36 moves, I suspect this can be reduced considerably - my first attempt had 60 moves and I only discovered formulae 9 & 10 today and they reduced stage 4 by 10 moves.
We now see exactly how many patterns are possible, namely
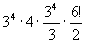 = 31 149280, as given by Tony Durham. This is based on the actual restoration process and one may prefer a different expression as
= 31 149280, as given by Tony Durham. This is based on the actual restoration process and one may prefer a different expression as
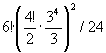 .
That is, the centres can be in any permutation and each tetrad can have its corners in any even permutation and twisted so the total twist is 0 (mod 3), but the whole cube has 24 equivalent placements.
.
That is, the centres can be in any permutation and each tetrad can have its corners in any even permutation and twisted so the total twist is 0 (mod 3), but the whole cube has 24 equivalent placements.
18
It was the 3s in the denominator which I missed before - and the above doesn't make them quite clear. The 4!/2 refers to the even permutations in one tetrad and the corresponding 34 refers to the corner twists in the other tetrad. The Theorem of stage 2 shows that there is an interaction between these so that only 1/3 of the combined possibilities are achieved. So perhaps a better expression is
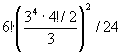 .
Incidentally, the odd permutations of the centres correspond to movements of the whole cube which interchange the tetrads. If we do not allow the tetrads to be interchanged, then both the 6! and the 24 are divided by 2.
.
Incidentally, the odd permutations of the centres correspond to movements of the whole cube which interchange the tetrads. If we do not allow the tetrads to be interchanged, then both the 6! and the 24 are divided by 2.
If we imagine one tetrad held in place, then our only moves are about its corners. E.g. if we consider 1, 3, 6, 8 as held in place, then we only consider the moves 1, 3, 6, 8 and their inverses. Then there are at most 1 + 8 + 8·6 + 8·62 + ... + 8·6n positions after n moves.
This is (8·6n - 3)/5 and this does not exceed 31 149280 until n = 9. That is, God's Algorithm must be at least 9 moves in diameter.
One might say that the Skewb is easily solvable - after all, we have a solution in at most 36 moves already and it will probably come down. But it is much less easy than this would indicate. It is very hard to keep track of movements since each move disrupts so much. I think it would be quite difficult to restore the Skewb after 3 random moves. Any false move usually is difficult to recover from. It takes a good eye and some practice to use a tetrad for orientation. It is a first class puzzle and I send my compliments to the inventor, Tony Durham.
In my Notes (N38), Kate Fried is reported as being able to invert up to 7 random moves from START on the 33. So 8 moves generally is enough to thoroughly randomise a 33. She reports that 4 moves are enough to randomise a Skewb.
GOD'S ALGORITHM FOR THE PYRAMINX
Douglas Hofstadter reports that John Francis (USA), Lothar Teichert (Germany) and Louis P. A. Bobichaud (Canada) have each found God's Algorithm for the Pyraminx. The four trivial vertex moves are ignored. The number Nd of positions at distance d from START is given in the table below. The average distance from START is 7.8.
| d | | Nd |
| 0 | | 1 |
| 1 | | 8 |
| 2 | | 48 |
| 3 | | 288 |
| 4 | | 172 |
| 5 | | 9896 |
| 6 | | 51808 |
| 7 | | 2 20111 |
| 8 | | 4 80467 |
| 9 | | 1 66276 |
| 10 | | 2457 |
| 11 | | 32 |
19
URIBLOCK
Dario Uri, of Bologna, has devised a different form of the 4 × 4 puzzles (C2-9, C5/6-7/8). This has a 4 × 4 field with each row and column able to slide by one square. However, there are only four pieces to a line, so that sliding a line introduces a rigid part of the slide at one end, making the perpendicular slide at that end now immovable. When the 4 × 4 field is in place, the rows and columns are able to slide, but in alternate directions. Thus the top row can go to the right, the second row can go to the left, the third row can go to the right, the fourth row can go to the left. It is convenient that the alternation of pattern is the same no matter which side is up, i.e. the left hand column can slide up. If the alternation is the other way in the second direction, then the corners do not all behave the same; instead there are three types of corner depending on whether none, one or two of the slides affecting it carry the corner out of the field. This would make the puzzle even harder.
The blockage of movement and the alternation of slides makes it not at all obvious how to solve the general puzzle. A little work shows that one can form a 3-cycle in the central 2 × 2 area and there is sufficient transitivity so that all even permutations seem to be readily achievable. As with all puzzles of this nature, only the even permutations are possible. If all the pieces are distinct, this gives us 16!/2 = 1046 13949 44000 patterns. In the actual puzzle, there are only four colours of piece, and four of each colour. This gives
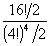 = 630 63000 patterns. The packaging says 63 millions of combinations, so that, for once, the right number is given! My thanks to Dario Uri for sending an example via David Lister. Pentangle is distributing the Uriblock in the UK.
= 630 63000 patterns. The packaging says 63 millions of combinations, so that, for once, the right number is given! My thanks to Dario Uri for sending an example via David Lister. Pentangle is distributing the Uriblock in the UK.
PS. The 2 × 2 Uriblock doesn't do anything, but the 3 × 3 Uriblock is solvable - i.e. any even permutation of the 9 squares is achievable. For the 3 × 3, we necessarily have that the alternation cannot be the same no matter which side is up and there are three types of corner.
MORE ON THE HUNGARIAN RINGS
I discussed the Hungarian Rings in C2-14 and their generalisation at C5/6-9/10. I have now seen the 19th century patent.
William Churchill, of Detroit, obtained US Patent 507,215 on 24 Oct 1893 for a Puzzle, which is conceptually identical to the Hungarian Rings. He permits various sizes of ring, but his drawing shows two rings of 22 pieces, with the intersections being 6 pieces apart on both rings. I.e. this is G(22, 22, 6, 6). His version has simple grooves, so that the pieces can be removed. Removal of one piece gives a sliding piece puzzle. He states the following problem for the puzzle with all pieces in. Start with 20 pieces of each of two colours and two pieces of a third colour. Put the two pieces at the intersections, 20 pieces of one colour in the rest of one ring and the 20 pieces of the other colour in the other ring. By clockwise rotations only, exchange the colours in the rings, leaving the intersections of the third colour. Churchill asserts it can be done in 340 moves!
My paper on the generalised Hungarian Rings groups has appeared in the Bulletin of the Institute of Mathematics and Its Applications 20:9/10 (Sep/Oct 1984) 137-139.
A G(6, 6, 2, 2) version called Rotos is made in East Germany.
20
SOME NOTES ON POLYHEDRA
One or the few products which caught my eye at the 1983 London Toy Fair was a new type of plastic piece for building polyhedra. This led me to the study of certain types of polyhedra. Then this summer, at the International Congress of Mathematicians at Warsaw, I saw a display of a recently discovered class of polyhedra which I have investigated further. These notes cover two topics: pieces for building polyhedra and classes of polyhedra.
 You may have seen some of the different ways of joining pieces. The most common method for cardboard pieces is the use of 'ears' along the edges as shown in Figures 1 - 3. The ears are folded and then joined by a rubber band over them. This idea was patented by Fred Bassetti, an architect from Portland, Oregon, , sometime in the 1960s. I still have a set given to me then and called Flexagons and containing the regular n-gons for n 3, 4, 5, 6, with edge length of 90mm. These were available, in lighter card and different colours, from Book-Lab Inc., 1449 37th St., NY, NY, 11218, but they had stopped production by 1980. A nice booklet by Bassetti and two others, entitled 'Math Projects: Polyhedral Shapes' , was also available.
You may have seen some of the different ways of joining pieces. The most common method for cardboard pieces is the use of 'ears' along the edges as shown in Figures 1 - 3. The ears are folded and then joined by a rubber band over them. This idea was patented by Fred Bassetti, an architect from Portland, Oregon, , sometime in the 1960s. I still have a set given to me then and called Flexagons and containing the regular n-gons for n 3, 4, 5, 6, with edge length of 90mm. These were available, in lighter card and different colours, from Book-Lab Inc., 1449 37th St., NY, NY, 11218, but they had stopped production by 1980. A nice booklet by Bassetti and two others, entitled 'Math Projects: Polyhedral Shapes' , was also available.
 |
 |
| FIGURE 2 |
FIGURE 3 |
Invicta Plastics (Oadby, Leicester, UK), best known for Mastermind, produced a large kit called Polyshapes, based on the same principle and apparently under license since some pictures are the same as in 'Math Projects' . They used heavy white card and an edge length of 70mm. The kit includes regular n-gons for n = 3, 4, 5, 6, 8, 10 and 70 by 140 mm rectangles and 70, 113, 113 mm isosceles triangles (with angles of 72°, 72° and 36°), (The Flexagons had different colours or patterns for each shape. Book-Lab kindly sent some samples when I wrote them. These were all blue and all orange - I don't know if they were mixed in their kits. The Invicta are all white.) Invicta supplies a set of 26 work cards by H. Shaw.
21
 I have seen a number of other methods of joining cardboard polygons, using tabs and slots, but I do not find them easy to use - either they come apart too easily or they don't come apart at all. Joining plastic pieces along a hinged edge is not as easy and I had only noted one attempt to do this before this year, though there may have been others I didn't know about. The object I had first seen was the Happy Cubes made by the US firm of Mag-Nif and unfortunately not available in the UK. This had eight cubes joined in a chain by the edge connection shown at the right1 Figure 14. Unfortunately, the plastic was a bit soft and the outer parts of the hinge were too rigid, so that the balls which fit in the sockets soon wore down and the puzzle would fall apart when you picked it up.
I have seen a number of other methods of joining cardboard polygons, using tabs and slots, but I do not find them easy to use - either they come apart too easily or they don't come apart at all. Joining plastic pieces along a hinged edge is not as easy and I had only noted one attempt to do this before this year, though there may have been others I didn't know about. The object I had first seen was the Happy Cubes made by the US firm of Mag-Nif and unfortunately not available in the UK. This had eight cubes joined in a chain by the edge connection shown at the right1 Figure 14. Unfortunately, the plastic was a bit soft and the outer parts of the hinge were too rigid, so that the balls which fit in the sockets soon wore down and the puzzle would fall apart when you picked it up.
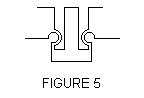 More recently, I have seen the Tri Logic of Mag-Nif. This has 24 triangles in plastic with hinges as shown on the right, Figure 5. Each edge has two of the hinges, one male part and one female part on each side of the edge. I haven't had mine long enough to see how sturdy it is. It does have the obvious disadvantage that they have tried to bring the edges to a real meeting point and this produces an extremely sharp point at each vertex.
More recently, I have seen the Tri Logic of Mag-Nif. This has 24 triangles in plastic with hinges as shown on the right, Figure 5. Each edge has two of the hinges, one male part and one female part on each side of the edge. I haven't had mine long enough to see how sturdy it is. It does have the obvious disadvantage that they have tried to bring the edges to a real meeting point and this produces an extremely sharp point at each vertex.
 Another version of idea is Clixi, produced by ESA Creative Learning, Harlow, UK. Their joint is shown on the right, Figure 6. Again each edge has two of the hinges, with one of each sex on each side. Clixi also provides squares, pentagons, circles and some cross pieces. The squares (at least) have joints moulded into the inside so that one can attach a piece to the interior of the square. This, and the circles and cross pieces, make this a much more general construction kit than the other kits described here. A 140 page booklet, 'Exploring Mathematics with 'Clixi', comes with it and is obviously aimed at 8-12 year olds. The corners are better rounded than in Tri Logic, but the pieces are supplied in moulded sheets and do not detach cleanly.
Another version of idea is Clixi, produced by ESA Creative Learning, Harlow, UK. Their joint is shown on the right, Figure 6. Again each edge has two of the hinges, with one of each sex on each side. Clixi also provides squares, pentagons, circles and some cross pieces. The squares (at least) have joints moulded into the inside so that one can attach a piece to the interior of the square. This, and the circles and cross pieces, make this a much more general construction kit than the other kits described here. A 140 page booklet, 'Exploring Mathematics with 'Clixi', comes with it and is obviously aimed at 8-12 year olds. The corners are better rounded than in Tri Logic, but the pieces are supplied in moulded sheets and do not detach cleanly.
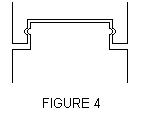
 The version that I saw at the Toy Fair this year seems to be definitely the nicest that I have seen. The hinge was devised by Edward Harvey and the pieces are being produced by Polydron UK, Unit 12, Staveley Way, Brixworth Industrial Estate, Brixworth, Northampton-shire, NN6 9EU, UK. The hinge is shown at right, Figure 7. Because of the intricacy, I have drawn only one side of the hinge. The other side is identical, just turned over. The pieces are thick and come in four primary colours with a smooth finish. The corners are neatly rounded.
The version that I saw at the Toy Fair this year seems to be definitely the nicest that I have seen. The hinge was devised by Edward Harvey and the pieces are being produced by Polydron UK, Unit 12, Staveley Way, Brixworth Industrial Estate, Brixworth, Northampton-shire, NN6 9EU, UK. The hinge is shown at right, Figure 7. Because of the intricacy, I have drawn only one side of the hinge. The other side is identical, just turned over. The pieces are thick and come in four primary colours with a smooth finish. The corners are neatly rounded.
22
At first, only equilateral triangles were produced, but squares became available in 1984. Since the pieces are thick, they are not cheap - a box of 60 retails at about £8.00. But bulk orders for educational use should be considerably cheaper and I think this will be a major market for the pieces, especially when other shapes become available. They seem ideal for classroom use. Polydron kindly sent me a bag of pieces to try out and I certainly find them the most pleasant to handle of all the types described.
In all of the hinges described, some flexibility must be designed in so that the ball and socket joint can be made of hard plastic which will not wear down. But this means that there is no give at the joint and go some give must be designed in elsewhere, again to prevent the joint wearing down. Mag-Nif's Happy Cubes failed to provide flexibility so the balls and sockets just ground each other down. All the other hinges have some sort of thin parts which bend and spring back as the pieces are snapped together or taken apart.
Once one has a kit of snap-together triangles, one wonders what one can build with them. In fact there are many such shapes and they have been called 'deltahedra', since an equilateral triangle looks like the Greek capital letter delta - Δ. Surprisingly, these have not been studied until quite recently - most authors cite a 1947 paper. But first we must note that one must make some restriction since it is easy to build infinitely many deltahedra - simply replace a face by a triangular pyramid on that face. This process can be repeated indefinitely. One can also build pleated tubes of arbitrary length. Most of the deltahedra constructed are non-convex, so we might ask for the convex ones. H. Freudenthal and B. L. van der Waerden, two eminent Dutch mathematicians, published 'Over een bewering van Euclides (On an assertion of Euclid)' in Simon Stevin 25 (1946/147) 115-121. They showed that there are just 8 convex deltahedra. It was later discovered that O. Rausenberger had found the same result in 'Konvexe pseudoreguläre Polyeder' in Zeitschr. fur math. und naturwiss. Unterricht 46 (1915) 135-142. The only English exposition I know of is in A. Beck, M. Bleicher & D. Crowe, 'Excursions in Mathematics', Worth, NY, 1969. A brief description is given in
H. Behnke, et al., 'Fundamentals of Mathematics', vol. 2, pp. 268-271, MIT Press, 1974. See next page for drawings.
Five of the deltahedra are fairly obvious. I, III, VIII are the regular tetrahedron, octahedron and icosahedron. II, III, IV are the triangular, square and pentagonal bipyramids. If we look at the icosahedron, VIII, we can imagine removing the top and bottom pentagonal pyramids and replacing them with pentagons. This gives what we call the pentagonal antiprism. In general, an n-gonal antiprism has two parallel n-gons, one turned by 360°/2n with respect to the other and the space in between filled by 2n equilateral triangles. The octahedron, III, is the triangular antiprism. VII and VIII are the square and pentagonal anti-prisms, with their n-gonal faces replaced by pyramids. (If you try this with the octahedron, the triangular faces pair off into rhombuses and you get a rhombic parallelepiped.) VI is obtained from VII by replacing one of the square pyramids with two triangles. This can also be obtained by starting with a triangular prism and replacing each square face by a square pyramid. V is obtained from VI by replacing one of these square pyramids by two triangles. (Repeating the process gives the pentagonal bipyramid, then the octahedron, then the triangular bipyramid, then the tetrahedron!)
24
The work of Freudenthal and van der Waerden was inspired by reading Euclid, XIII, 18, which asserts (in Heath's translation) that there are only five figures which are "contained by equilateral and equiangular figures equal to one another". Euclid doesn't contemplate non-convex or infinite polyhedra, but the 5 non-regular convex deltahedra certainly still fit Euclid's definition. There are no other cases, since squares and pentagons can only fit with three at each vertex and thereby only give the regular polyhedra
Euclid intended to consider polyhedra whose symmetry group was transitive on vertices, edges and faces. That is, each vertex (or edge or face) can be carried into any other by some symmetry of the solid. Otherwise stated, all vertices, edges and faces appear the same. For a non-regular deltahedron such as the triangular bipyramid (II), some vertices have 3 edges while some have 4, so they are not all the same. Some edges join pairs of 3-fold vertices while others join a 3-fold and a 4-fold vertex, so they are not all the same. But all the faces are the same However, the faces are not all the same on V, VI or VII. By relaxing the criteria that Euclid intended, we can extend the family of regular polyhedra in several ways. Below, I outline several of these ways. The interested reader can find fuller details in the following.
H. Behnke, et al. Fundamentals of Mathematics. Vol. II - Geometry. MIT Press, 1974.
H. S. M. Coxeter. Regular Polytopes. 2nd ed. Macmillan, 1963.
H. M. Cundy & A. S. Rollett. Mathematical Models. 2nd ed., Oxford Univ. Press, 1961.
L. Lines. Solid Geometry. Dover, 1965
M. J. Wenninger. Polyhedron Models. Cambridge Univ. Press, 1971.
A. REGULAR POLYHEDRA
First, let us review the regular or Platonic polyhedra and lattices. The basic argument for these and most other polyhedra is that the sum of the angles at each vertex must be less than 2π (= 360°). (Equality leads to another type of figure - the plane lattices or tessellations.) The angle at the corner of a regular p-gon is (p-2)π/p. If we have q p-gons at a vertex, then we must have q(p-2)π/p <= 2π. This gives pq - 2q <= 2p, hence pq -2q - 2p <= 0, hence pq - 2q - 2p + 4 <= 4, i.e.
(*) (p - 2)(q - 2) <= 4.
For a convex polyhedron with V vertices, E edges and F faces, we also have Euler's formula. V - E + F = 2. For a regular polyhedron with p, q as above, we have pF = qV = 2E, since pF and qV both count all the edges twice over - pF counts them from each side, while qE counts them from each end. Hence (2/q - 1 + 2/p)E = 2, or (2p + 2q - pq)E = 2pq and E = 2pq/(2p+2q-pq). The fact that this denominator must be >= 0 is just (*) again.
There are not many solutions of (*), if we remember that p, q >= 3.
| p | q | V | E | F |
| 3 | 3 | 14 | 6 | 4 | Tetrahedron |
| 3 | 4 | 6 | 12 | 8 | Octahedron |
| 4 | 3 | 8 | 12 | 6 | Cube |
| 3 | 5 | 12 | 30 | 20 | Icosahedron |
| 5 | 3 | 20 | 30 | 12 | Dodecahedron |
| 3 | 6 | - | - | - | Triangular lattice |
| 6 | 3 | - | - | - | Hexagonal lattice |
| 4 | 4 | - | - | - | Square lattice |
25
 I have drawn bits of the triangular and hexagonal lattices to the right since these are the least familiar of the above solutions. These figures are often denoted by the Schläfli symbol {p, q}. The figure {p, q) is dual to the figure {q, p} in that the roles of vertices and faces are interchanged. E.g. the octahedron has 6 vertices and 8 faces, while its dual, the cube, has 8 vertices and 6 faces. The easiest way to construct a dual is to take new vertices at the centres of the old faces and join these if the corresponding old faces are adjacent. I have bracketed the dual pairs in the table on the preceding page. Note that (3,3) and {4,4} are self-dual.
I have drawn bits of the triangular and hexagonal lattices to the right since these are the least familiar of the above solutions. These figures are often denoted by the Schläfli symbol {p, q}. The figure {p, q) is dual to the figure {q, p} in that the roles of vertices and faces are interchanged. E.g. the octahedron has 6 vertices and 8 faces, while its dual, the cube, has 8 vertices and 6 faces. The easiest way to construct a dual is to take new vertices at the centres of the old faces and join these if the corresponding old faces are adjacent. I have bracketed the dual pairs in the table on the preceding page. Note that (3,3) and {4,4} are self-dual.
The regular polyhedra have all vertices, edges and faces the same and they are finite and convex. Removing finiteness in one way gives the regular tessellations or lattices.
B. KEPLER-POINSOT POLYHEDRA
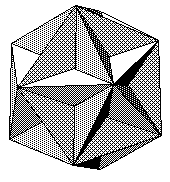
 If we remove the condition that our figure is convex, we obtain Is further polyhedra called the Kepler-Poinsot polyhedra. The great dodecahedron is just the shape of Alexander's Star (C3/4-19/20) - it has five pentagons meeting at each vertex in a pentagram pattern, as shown at the right. The great icosahedron has five triangles meeting at each vertex in a pentagram pattern. These were discovered by Poinsot in 1809. The duals of these are polyhedra whose faces are pentagrams. The small stellated dodecahedron has five faces at each vertex in a pentagonal pattern and looks like a dodecahedron with pentagonal pyramids on each face. The great stellated dodecahedron is actually a stellation of the great dodecahedron and looks like each of the triangular hollows of the great dodecahedron has been filled out to a pyramid. These were discovered by Kepler (in his De Harmonice Mundi, 1609, a work better known for the first appearance of Kepler's Third Law), and were rediscovered by Poinsot. The great icosahedron and the great stellated dodecahedron were rediscovered by Schläfli in 1901, but he did not believe the other two could exist because they do not satisfy Euler's formula, even when adjusted to make the first two satisfy it! It is possible to demonstrate that there are no further examples of this family of polyhedra, but the proof takes some work. See Coxeter, Chapter VI. The pentagram is conveniently denoted by 5/2, where the 2 denotes the connection from a vertex to the one that is two away. In general, the various star-polygons are denoted by rational numbers and one of the approaches to showing there are no further polyhedra in this class depends on seeing that there are no further rational solutions of a certain trigonometric relationship. Coxeter's first approach is to see that a regular polyhedron in our present extended sense has a symmetry group which is the same as the symmetry group of a Platonic regular polyhedron and this depends on some careful analysis of three-dimensional symmetry groups. Once this is established, one has only to examine the various stellatings of the dodecahedron to find all the possible cases.
If we remove the condition that our figure is convex, we obtain Is further polyhedra called the Kepler-Poinsot polyhedra. The great dodecahedron is just the shape of Alexander's Star (C3/4-19/20) - it has five pentagons meeting at each vertex in a pentagram pattern, as shown at the right. The great icosahedron has five triangles meeting at each vertex in a pentagram pattern. These were discovered by Poinsot in 1809. The duals of these are polyhedra whose faces are pentagrams. The small stellated dodecahedron has five faces at each vertex in a pentagonal pattern and looks like a dodecahedron with pentagonal pyramids on each face. The great stellated dodecahedron is actually a stellation of the great dodecahedron and looks like each of the triangular hollows of the great dodecahedron has been filled out to a pyramid. These were discovered by Kepler (in his De Harmonice Mundi, 1609, a work better known for the first appearance of Kepler's Third Law), and were rediscovered by Poinsot. The great icosahedron and the great stellated dodecahedron were rediscovered by Schläfli in 1901, but he did not believe the other two could exist because they do not satisfy Euler's formula, even when adjusted to make the first two satisfy it! It is possible to demonstrate that there are no further examples of this family of polyhedra, but the proof takes some work. See Coxeter, Chapter VI. The pentagram is conveniently denoted by 5/2, where the 2 denotes the connection from a vertex to the one that is two away. In general, the various star-polygons are denoted by rational numbers and one of the approaches to showing there are no further polyhedra in this class depends on seeing that there are no further rational solutions of a certain trigonometric relationship. Coxeter's first approach is to see that a regular polyhedron in our present extended sense has a symmetry group which is the same as the symmetry group of a Platonic regular polyhedron and this depends on some careful analysis of three-dimensional symmetry groups. Once this is established, one has only to examine the various stellatings of the dodecahedron to find all the possible cases.
26
GREAT DODECAHEDRON |

GREAT ICOSAHEDRON |
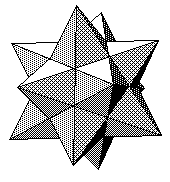
GREAT STELLATED DODECAHEDRON |

GREAT STELLATED ICOSAHEDRON |
| p | q | V | E | F |
| 5/2 | 5 | 12 | 30 | 12 | Great dodecahedron |
| 5 | 5/2 | 12 | 30 | 12 | Small stellated dodecahedron |
| 5/2 | 3 | 12 | 30 | 20 | Great icosahedron |
| 3 | 5/2 | 20 | 30 | 12 | Great stellated dodecahedron |
C. HONEYCOMBS
If we remove the conditions of both finiteness and convexity, we can get infinite 'honeycombs'. For example, consider all the faces of the regular cubical lattice. By removing half of these faces, like the black squares on a chessboard, along each plane, one can get an arrangement which divides space into two congruent halves, sometimes called sponges. If one thinks of the basic unit as 2 × 2 × 2 box of 8 cells, indefinitely repeated, then one half consists of a cube and its three neighbours, forming a 'pyramid' at a corner (as described in C5/6-12), repeated indefinitely. Many other patterns are possible, by using different sizes and halvings of units and by using other space filling polyhedra, such as the rhombic dodecahedron or the truncated octahedron, These get quite complex and Coxeter has written a booklet on them: 'Twisted Honeycombs', Amer. Math. Soc., 1970.
27
D. SEMI-REGULAR POLYHEDRA
Let us reinstate our assumptions that our polyhedra are convex and finite, but remove the assumption that all faces are the same, only requiring that all vertices and edges are the same, and that the faces are regular polygons. Then there are only two types of face - one on each side of each edge - and they must alternate about each vertex. Since the sum of the angles at each vertex must be C 2s, we find just three possibilities. Let the polygons be p1 and p2-gons. A little consideration of the possibilities shows that we must have 4 polygons at each vertex and hence (p1-2)/p1 + (p2-2)/p2 <= 1. Our three cases, beyond the Platonic cases, are then given by the table.
| P1 | P2 | V | E | F1 | F2 |
| 3 | 14 | 12 | 24 | 8 | 6 | Cuboctahedron (C1-7) |
| 3 | 5 | 30 | 60 | 20 | 12 | Icosidodecahedron |
| 3 | 6 | - | - | - | - | Lattice of triangles and hexagons |
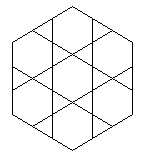 Each of these is a mixture of two dual figures and can be viewed several ways. If we start with a cube and truncate its corners more and more until the triangles formed at the corners just touch, then we have the cuboctahedron. Truncating further leads to the octahedron. We can also truncate the octahedron to get the cuboctahedron and then the cube. We can see that the vertices of the cuboctahedron correspond to the edges of the cube (or octahedron) while the faces correspond to the faces and the vertices of the cube (or octahedron). We have p1F1 = p2F2 = E.
The icosidodecahedron is similarly the truncation of the dodecahedron or the icosahedron. The lattice of triangles and hexagons, shown on the right, can be viewed as a truncation of {3,6} or {6,3}, but it may be easier to see by taking the triangular or hexagonal lattice and placing new vertices in the centre of each edge and joining the vertices of adjacent edges, where adjacent means having a common vertex and a common face. These figures were certainly known to the Greeks. Archimedes, in a lost account, ascribes the cuboctahedron to Plato, and Archimedes describes the icosidodecahedron.
Each of these is a mixture of two dual figures and can be viewed several ways. If we start with a cube and truncate its corners more and more until the triangles formed at the corners just touch, then we have the cuboctahedron. Truncating further leads to the octahedron. We can also truncate the octahedron to get the cuboctahedron and then the cube. We can see that the vertices of the cuboctahedron correspond to the edges of the cube (or octahedron) while the faces correspond to the faces and the vertices of the cube (or octahedron). We have p1F1 = p2F2 = E.
The icosidodecahedron is similarly the truncation of the dodecahedron or the icosahedron. The lattice of triangles and hexagons, shown on the right, can be viewed as a truncation of {3,6} or {6,3}, but it may be easier to see by taking the triangular or hexagonal lattice and placing new vertices in the centre of each edge and joining the vertices of adjacent edges, where adjacent means having a common vertex and a common face. These figures were certainly known to the Greeks. Archimedes, in a lost account, ascribes the cuboctahedron to Plato, and Archimedes describes the icosidodecahedron.
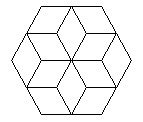 The duals of these figures are less obvious. They are figures with all faces and edges being the same and the vertices are regular. This means that the pattern of faces at a vertex forms a regular polygon. These are less easy to see and hence have not been investigated as much. The faces are all rhombuses, but with different angles. The polyhedral ones are the rhombic dodecahedron and the rhombic triacontahedron. The rhombic dodecahedron is described in C5/6-12/14, but sketchily
The duals of these figures are less obvious. They are figures with all faces and edges being the same and the vertices are regular. This means that the pattern of faces at a vertex forms a regular polygon. These are less easy to see and hence have not been investigated as much. The faces are all rhombuses, but with different angles. The polyhedral ones are the rhombic dodecahedron and the rhombic triacontahedron. The rhombic dodecahedron is described in C5/6-12/14, but sketchily
.
The rhombic triacontahedron, with 30 faces, can be obtained as a die. Both of these are attributed to Kepler, but there is an article: F. Lindemann, Zur Geschichte der Polyeder und der Zahlzeichen, Sitzungsberichte der math.-phys. Classe k. b. Akademie der Wissenschaften zu München 26 (1896) 625-783 & 9 plates, which describes an antique rhombic triacontahedron. He thinks it may date from about the middle of the Byzantine era. The dual of the lattice, shown on the right, is a famous optical illusion and a common patchwork quilt pattern called 'baby blocks'.
28
E. ARCHIMEDEAN POLYHEDRA
If we remove the assumption that all edges are the same, but still ask for regular faces, there are still only a few possibilities for the angles at each vertex. There are two infinite families of such polyhedra - the prisms Πn and the antiprisms An. There are just 13 more such polyhedra, though two types have right- and left-handed forms. These were known to Archimedes, according to a lost account which was summarised by Pappus. To classify these, we represent the pattern of polygons around a vertex by simply listing them in order and abbreviating repetitions by use of powers. E.g. the vertex pattern of a cube is 444 or 43, while the vertex pattern of a cuboctahedron is 3434 or (34)2.
| Number | Vertex
pattern | V | E | F1,F2,F3 | F |
| I | 42n | 2n | 3n | n,2 | n+2 | n-prism, Πn |
| II | 362 | 12 | 18 | 4,4 | 8 | Truncated tetrahedron |
| III | 462 | 24 | 36 | 6,8 | 14 | Truncated octahedron |
| IV | 562 | 60 | 90 | 12,20 | 32 | Truncated icosahedron |
| V | 382 | 24 | 36 | 8,6 | 14 | Truncated cube |
| VI | 3.102 | 60 | 90 | 20,12 | 32 | Truncated dodecahedron |
| VII | (34)2 | 12 | 24 | 8,6 | 14 | Cuboctahedron |
| VIII | (35)2 | 30 | 60 | 20,12 | 32 | Icosidodecahedron |
| IX | 33n | 2n | 4n | 2n,2 | 2n+2 | n-antiprism, An |
| X | 343 | 24 | 48 | 8,18 | 26 | (Small) Rhombicuboctahedron |
| XI | 344 | 24 | 60 | 32,6 | 38 | Snub cube |
| XII | 345 | 60 | 150 | 80,12 | 92 | Snub dodecahedron |
| XIII | 468 | 48 | 72 | 12,8,6 | 26 | Great rhombicuboctahedron |
| XIV | 4.6.10 | 120 | 180 | 30,20,12 | 62 | Great rhombicosidodecahedron |
| XV | 3454 | 60 | 120 | 20,30,12 | 62 | (Small) rhombicosidodecahedron |
The two great rhombi-s can be viewed as truncations of the corresponding polyhedra, but the natural truncation leads to rectangular faces, as with the object shown at C1-9. But adjusting the truncation a bit, one gets square faces. There is a pseudo-Archimedean polyhedron obtained by rotating one 'face' (in the Rubik Cube sense) of the rhombicuboctahedron (X) by 45°, i.e. an eighth turn. Each vertex then has the same pattern, but they are not all the same on the polyhedron as a whole.
29
THE ARCHIMEDEAN POLYHEDRA
30
The dual Archimedean polyhedra have all their faces the same, but they are not regular. Consequently, few of these are well known. We have seen the duals of the semiregular polyhedra in the previous section. The dual of a prism is a bipyramid. The dual of an antiprism is a trapezohedron.
F. ARCHIMEDEAN TESELLATIONS
If we make the sum or the angles at each vertex now be 2π, we have the planar tessellation analogues of the Archimedean polyhedra. It turns out there are just 8 of them, having the following vertex patterns.
3342, 32434, (36)2, 346, 3.122, 482, 4.6.12, 3464.
346 has right- and left-handed forms. (36)2 is semi-regular.
 |
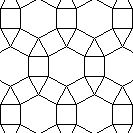 |
| 4·6·12 |
3464 |
31
G. UNIFORM POLYHEDRA
If we drop the assumption of convexity from the concept of Archimedean polyhedron, we have the concept of polyhedra with all vertices the same, and with all faces regular, but possibly star-polygons. These are called uniform polyhedra. The Platonic and Archimedean polyhedra are the convex uniform polyhedra. In general, a non-convex uniform polyhedron looks like an ordinary polyhedron with some bits missing. The simplest example consists of the three square cross-sections of an octahedron, with half of the octahedral faces filled in. Then each vertex has two squares and two triangles. The result is a most peculiar polygon - it only has one side!
The uniform polyhedra have been discovered by a number of people over the last century: Badoureau (1881), Hess (1878), Pitsch (1881), Coxeter and Miller (1930-1932), M. S. & H. C. Longuet-Higgins (1942-1944), Lesarve and Mercier (1947). These results are all presented in:
H. S. M. Coxeter, M. S. Longuet-Higgins & J. C. P. Miller. Uniform polyhedra. Philos. Trans. Roy. Soc. 246A (1954) 401-450. Their end result is that there are at least 53 uniform polyhedra, beyond the 5 Platonic, 13 Archimedean, 14 Kepler-Poinsot and the prisms and anti-prisms. They say: 'it is the authors' belief that the enumeration is complete, although a rigorous proof has still to be given'. Wenninger's book, cited earlier, shows how to construct all 75 of these, where this number excludes Πn, n != 4, and An, n > 3. (Π4, the cube, and A3 the octahedron, fall into the 75 in other ways.)
H. REGULAR-FACED POLYHEDRA
The most recent of the generalisations of the regular polyhedra is the removal of all symmetry to ask: what convex polyhedra can be formed with regular polygonal faces? This has only been resolved in the 1960s. I heard something about it from Dick Hess in 1983 , but my knowledge of it derives from a marvellous exhibition by Professor S. Zych of Bialystock at the International Congress of Mathematicians in Warsaw, summer, 1983. Following on Zych's information, I have found the basic papers. These are;
Norman W. Johnson. Convex polyhedra with regular faces. Canad. J Math. 18 (1966) 169-200. (Johnson also produced an identically titled set of lecture notes at Carleton College, 1961).
Viktor A. Zalgaller. Convex polyhedra with regular faces. Seminars in Mathematics, V. A. Steklov Mathematical Institute, Leningrad, vol. 2, (1967) - in Russian. English translation: Consultants Bureau, NY, 1969, 95pp.
The regular-faced polyhedra are:
the prisms Πn, n >= 3;
the antiprisms An, n >= 3;
the 5 regular, Platonic, polyhedra;
the 13 Archimedean polyhedra;
92 others.
A regular-faced polyhedron is simple if it cannot be cut into two such polyhedra. Otherwise it is composite. For example, an octahedron can be cut into two square pyramids. Note that Π6 can be cut into 6 Π3's, but is still simple. Johnson had obtained the above described polyhedra, but without complete proof. Zalgaller furnished the proof and introduced the notions of simplicity and compositeness. Zalgeller found that the simple regular-faced polyhedra are:
the prisms Πn, n >= 3;
the antiprisms An, n >= 4;
28 others.
32
The tetrahedron and dodecahedron are among the 28; the cube is Π4 and is simple; the octahedron (= A3) and the icosahedron are composite. The larger two irregular deltahedra (VII and VI) are composite, but V is simple. Zalgaller gives names to all these polyhedra: V is the snub disphenoid, VI is the triaugmented triangular prism, VII is the elongated square dipyramid.
An early result in this field by Branko Grünbaum and Johnson is that, except for prisms and antiprisms, the only n-gons that can occur are for n = 3, 4, 5, 6, 8, 10. Consequently these can all be built if you have enough or the Invicta Polyshapes kits. Professor Zych had a display of all these. Interestingly, he used hand cut pieces of coloured fibreglass exactly in the pattern of the eared polygons that started off this whole essay!
I. TESSELLATIONS AND TILINGS
We have already seen the 11 Archimedean tessellations in A (the 3 regular ones) and G (the 8 others). These are apparently due to Kepler. There are 10 further ways one can place regular n-gons around a vertex
in the plane: 32.4.12, 3.4.3.12, 3262, 3426, 3.7.14, 3.8.24, 3.9.18, 3.10.15, 4.5.20, 52.10. There are four cases where the same polygons can be arranged in different ways: 3342 - 32434, 32.4.12 - 3.4.3.12, 3262 - (36)2, 3426 - 3464. In all but the second case, it is possible to combine vertices of both orders to get non-Archimedean tilings of the whole plane. In the latter two cases, all the tilings are obtainable from the Archimedean ones by shifting part of the pattern. In the first case, the possible tilings are not all known.
On a sphere, the Archimedean tessellations are just the projections of the Platonic and Archimedean polyhedra, but there are a number of subdivisions of these which have some sort of regularity. For example, if one subdivides the pentagons of a dodecahedron into 10 triangles by drawing rays from the centre to the vertices and midpoints of sides, then one gets a spherical tessellation into 120 triangles. The symmetry group of the dodecahedron is precisely transitive on these triangles in the sense that there is a unique symmetry carrying a given triangle onto another one.
Our approach to finding these polyhedra and tessellations was by use of angles. It is possible to use Euler's formula for polyhedra and thereby show that they have their combinatorial structure determined. For tessellations, Euler's formula does not apply. But if one examines a finite region of expanding size, then one can get a limiting form of Euler's formula. This can be used to show that the Archimedean tessellations have their combinatorial structure determined. In both cases, it is a happy accident that these structures can be formed with regular polygons.
Let us now consider removing the criterion of building these structures with regular polygons. For example, consider a brick or a tiling by rectangles. Then the only condition we are imposing is that the symmetry group acts transitively on vertices. The symmetry group of such an object will be a subgroup of the symmetries when all the faces are regular. Using an appropriate definition of 'same type', it is a finite, though tedious, task to determine all the different types of polyhedra or tessellations. It is probably easier to consider the dual problem, which considers polyhedra or tessellations in which the symmetry group acts transitively on the faces or tiles. I do not know if this task has been done for polyhedra.
33
It has recently been carried out for tessellations by B. Grünbaum and G. C. Shephard. (See their survey papers. Tiling with congruent tiles. Bull. Amer. Math. Soc. 3 (1980) 951-973. Tilings by regular polygons. Math. Mag. 50 (1977) 227-2147.) They say a tiling is isohedral if its symmetry group acts transitively on the tiles. In particular, all tiles must be congruent. By examining the duals of the 11 Archimedean tessellations, they find that there are 81 types of isohedral tilings. (The tiles need not even be polygons!) They do not describe the duals of these, but it seems apparent that one can form some sort of duals, which would be tilings whose symmetries are transitive on vertices. Interestingly, the sphere has 8 infinite families and 53 other types of isohedral tilings on the sphere.
Grünbaum and Shepherd have also studied tilings with a single shape of tile, but where the symmetries are not transitive on the tiles. There are tiles which tile the plane or space, but which have no isohedral tilings. Indeed, there are convex pentagons with this property.
Any triangle or quadrilateral tiles the plane isohedrally. (Exercise: show this.) There are just 3 types of convex hexagon which tile the plane and there are no convex p-gons, for p >= 7. At present, there are 13 known types of convex pentagon which tile, though some are not 'edge to edge'. There have been several claims to a complete list in the past, but no one presently claims the list is complete. (See D. M. Schattschneider. Tiling the plane with congruent pentagons. Math. Mag. 51 (1978) 29-44 for the history and diagrams.)
It is often asserted that there are only a few space-filling solids. These are sometimes even listed: cube, hexagonal prism, rhombic dodecahedron, elongated dodecahedron (obtained from the rhombic dodecahedron by stretching along a diameter through two 4-fold vertices), truncated octahedron. But these are the parallelohedra, i.e. the convex polyhedra which fill space entirely by translations. No one knows all the space filling solids, even if we exclude the prisms over the tilings of the plane. In the first cited Grünbaum and Shephard paper, many peculiar space filling shapes are shown and described, including 14 types of convex polyhedra with 38 faces.
In C above, I described, rather vaguely, the idea of a honeycomb. Technically, Coxeter uses honeycomb for the filling of space by polyhedra and the infinite polyhedra obtained by considering some of their faces are called sponges. Coxeter showed there are three regular sponges: {4, 6}, {6, 4}, {6, 6}, using the Schläfli symbol in an obvious way. The first comes from the cubical lattice as I described in C. The second comprises the hexagons in the filling of space with truncated octahedra. I have not yet been able to see what the last one looks like. Aha! I've just tried again and I managed to find out what this is. Consider the truncated tetrahedron, which has 4 hexagonal and 4 triangular faces. This does not fill space, but if we also use tetrahedra which fit the triangular faces, then we can pack four truncated tetrahedra around each tetrahedron, face to face with it, then we can pack another six truncated tetrahedra edge to edge with the original tetrahedron and this leaves four gaps at the vertices which we fill with four of the small tetrahedra. The faces of the pieces fall into planes where the hexagons and triangles form the semi-regular tessellation described in B above. In a sense, this is the best possible packing of space with tetrahedra - it can't be done properly, but if we let the tetrahedra overlap at corners, then we have this packing, where the small tetrahedra are the overlaps of the main tetrahedra. The packing of space by truncated octahedra can be viewed similarly as a packing by octahedra which overlap in little octahedra. In this case, one can truncate the octahedra regularly to eliminate all overlaps. In the tetrahedral case, this cannot be done, but we can truncate three corners of the tetrahedron to obtain a shape which fills space. There is another way to fill space that is suggested by these ways. Take an octahedron and add two tetrahedra on adjacent faces of it. The result looks a bit like a fish and copies of it can be joined nose to tail to produce a rhombic prism stretching to infinity. These can be packed side by side to fill space.
34
ADDENDUM
I have recently attended the 1984 London Toy Fair and visited the Polydron stand. They have been doing well. They have improved the finish on their pieces and have started making squares. They will provide en educational kit of 100 triangles for £11.50, including postage and VAT.
A new type of piece was on display. This is called Model Eight and their address is: Model 8, Ltd., Unit 14, Little Marcle Road, Ledbury, Herefords., HR8 2DS.
 The mechanism is quite intricate and fits together in two basic ways. The first diagram on the right shows the basic shape of the piece, although the actual pieces are hollow in the middle. The projecting teeth have cylindrical rods or hollows on them which provide the axis of rotation. There are two types of edge: male with rods projecting from the teeth and female with hollows in the teeth. These are shown in the diagrams below. Because of the alternating nature of the teeth, a male and a female can be joined in two ways.
The mechanism is quite intricate and fits together in two basic ways. The first diagram on the right shows the basic shape of the piece, although the actual pieces are hollow in the middle. The projecting teeth have cylindrical rods or hollows on them which provide the axis of rotation. There are two types of edge: male with rods projecting from the teeth and female with hollows in the teeth. These are shown in the diagrams below. Because of the alternating nature of the teeth, a male and a female can be joined in two ways.
 The more natural is the join of the first diagram on the left with the second one. Then the pieces can rotate about the cylindrical axis. The less obvious join is of the first diagram with the third one. Then the teeth overlap and form a rigid joint.
The more natural is the join of the first diagram on the left with the second one. Then the pieces can rotate about the cylindrical axis. The less obvious join is of the first diagram with the third one. Then the teeth overlap and form a rigid joint.
An extra feature is that four pieces can be joined along an edge!
35
However, joining edges in the second way requires keeping the two pieces in one plane. Otherwise the rods can snap off rather easily.
I find joining the pieces is somewhat fiddly. The pieces are only about half the edge length of the Polydron pieces (32.5mm versus 70mm). Further, the arrangement of male and female edges must vary on the pieces. Triangles have two edges of one sex and one of the other and you need both types to build anything. As I recall, there are also two types of squares, one with the two male edges adjacent and one with them opposite. Only triangles and squares are available so far.
The makers advertise Model 8 'from six years' but I do not think primary children will find them very pleasing, though the makers show some complex objects made by 8 to 10 year olds. I don't think it will compete with Polydron for primary use, but it could have use for older children and adults. Since it is smaller and hollow, it should be much cheaper. Being hollow gives the constructions a linear rather than a solid appearance which can be more pleasing for some objects. If pentagons, hexagons, octagons, decagons and dodecagons are produced, the smaller size of Model 8 and the cheaper price may become dominant considerations for serious model builders.
SLIDING CUBE PUZZLES
On C2-9/10, I discussed sliding cube puzzles and cited Rouse Ball (1892). I have found an even earlier reference. P. G. Tait, in a Note on the Theory of the "15 Puzzle" (Proc. Roy. Soc. Edinburgh 10 (1878-1880) 664-665) says: "The principle above stated is, of course, easily applicable to the conceivable, but scarcely realisable, case of a rectangular arrangement of equal cubes with one vacant space."
The Japanese firm of Kawada is making and marketing a very nice seven cube version in a Piet Hein range. They are also doing a new version of his Soma Cube. This has solid versions of the domino, both trominoes and 4 of the tetrominoes as shown below. These total 24 cubes and the puzzle comes on a 3 × 3 base with a pillar up through the centre.
36
A RUBRIC ON RUBIK CUBICS1
By Claude E. Shannon
[Readers may remember that I referred to this song in C3/4-2. Shannon has sent an amended version. This song is probably unique in musical history in having 15 footnotes for only 6 verses. I have inserted the footnotes after each verse, except for the first, which is a footnote to the title and comes just below. I have corrected a few errors , indicated by use of square brackets.]
1. When T. S. Eliot published 'The Waste Land" in 1922 with a wealth of footnotes, there was considerable commotion among the critics - should a work of art stand on its own feet or refer to such weighty tomes as The Golden Bough. The ambiguity, obscurity and even prurience of modern poetry are also under attack. We intend this to be clean as a hound's tooth, crystal clear, sensible as a dictionary, and with footnotes galore.
First off, this may be either read as a poem or, better, sung to "Ta! Ra! Ra! Boom De Ay!" (with an eight bar chorus). The verses should be sung solo, in a slightly bitter sardonic manner, a la Noel Coward or Bea Lillie; the choruses, in contrast, a joyous rousing salute to the cube.
Once puzzledom was laissez faire
With rebus, crosswords, solitaire.
Comes now the Rubik Magic Cube
For Ph. D. or country rube.
This fiendish clever engineer
Entrapped the music of the sphere.
It's sphere on sphere in all 3 D -
A kinematic symphony!
Ta! Ra! Ra: Boom De Ay!
One thousand bucks a day.
That's Rubik's cubic pay.
He drives a Chevrolet.2
2. A little poetic license here - the Wall Street Journal, Sept. 23, 1981, reports Rubik as receiving $30,000 a month from cubic royalties, but driving a "run-down rattling Polski Fiat". This would neither scan nor rhyme as well as Chevrolet.
Forty-three quintillion plus3
Problems Rubik posed for us.
Numbers of this awesome kind
Boggle even Sagan's mind.4
Some chaps pry their cubes apart
Then reassemble to the "start"
Not cricket! a rude game's afoot
And up with which we will not put!
Ta! Ra! Ra! Boom De Ay!
Cu-bies in disarray?
First twist them that-a-way,
Then turn them this-a-way.
3. There are 8! 12!/2 38/3 212/2 = 43252 00327 44898 56000 possible arrangements of the cube.
4. It would take billions and billions of "billions and billions" for forty-three quintillion plus.
37
Respect your cube and keep it clean.
Lube your cube with Vaseline.
Beware the dreaded cuber's thumb,
The callused hand and fingers numb.5
No borrower nor lender be.
Rude folk might switch two tabs on thee,
The most unkindest switch of all,
Into insolubility.6
In-sol-u-bility.
The cruellest place to be.7
However you persist
Solutions don't exist.
5. While not as debilitating as weaver's bottom or hooker's elbow, cuber's thumb can be both painful and frustrating. For more on these occupational ailments see recent issues of "The New England Journal of Medicine".
6. A friend of mine, Pete, an expert cuber, told me of encountering a friend Bill at a hobby shop. Bill gave Pete his cube, saying that he had been working for days without success. After a few minutes, Pete turned it into a position where he could see that two tabs had been interchanged.
Pete: Bill, somebody has switched two tabs on your cube.
Bill: That's impossible. I've always carried it, or left it in my apartment, and nobody has keys to get in there.
Pete: Nobody?
Bill: That's right, nobody. Just me and my girlfriend.
7. Especially in April.
While most folk watch the idiot tube
Cubemeisters spin the Rubik cube.
Minh Thai's the champ - he's fast as sin.
Minh solves his cube in half a min.8
John Conway leads a Cambridge pack
And solves his cube behind his back.9
Singmaster wrote THE BOOK - first rank;
Now cubes while riding to the Bank.10
Here now a heavyweight
Programming potentate:
Software sophisticate:
Morwen B. Thistlethwaite!11
8. Minh Thai, World Speed Champion, in a public demonstration solved six scrambled cubes, each in less that 30 seconds.
9, Actually, he peeks a little. John Conway, the great Cambridge combinatorialist, in addition to his tour de force blindfold cubing has, with his colleagues, contributed much to Rubik cube theory.
10. Singmaster, David. Notes on Rubik's Magic Cube, now in its sixth edition. [Fifth edition, but who's counting!]
11. A pioneer in programming computers to solve the cube. His program solves the cube in 52 or fewer moves.
38
Eschewing this dull 3 D space
Joe Buhler cubes in hyperspace.12
All hail Dame Kathleen Ollerenshaw,
A mayor with fast cubic draw,13
Is cubing just a crashing bore?
Let Talken's robot do this chore.14
God moves in geodesic ways
And solves His cube in twenty plays.15
Cubemeisters one and all,
Their cubes find final rest
Bronzed in the Hall of Fame
In lovely Budapest.
12. Group theorist Buhler and his colleagues have developed a theory of higher dimensional cubes.
13. Renaissance woman, sometime mayor of Manchester, recreational mathematician, expert cubist and discoverer or the cubist thumb syndrome and its relation to the fetlock problem in horses.
14. In October 1981 the writer foresaw the need for a cubing machine and sketched the design of a pair of mechanical hands to be connected to a computer and manipulate a cube. In the summer of 1982 a crack team of one M.I.T. student was assembled. Late in July the hands were making their first fumbling attempts to hold and manipulate a cube, when we received a crushing newspaper clipping from a friend. It seems that Dan Talken had assembled a crack team of Southern Illinois University students and beat us to the punch. My friend wrote one word across the clipping: "scooped!"
15. Or so Singmaster finds it tempting to conjecture.
The battle's joined in steely grip;
Man's mind against computer chip,
With theorems wrought by Conway's eight
'Gainst programs writ by Thistlethwaite.
Can multi-billion neuron brains
Beat multi-megabyte machines?
The thrust of this theistic schism -
To ferret out God's algorism!
CODA:
He (hooked on cubing) with great enthusiasm:
Ta! Ra! Ba! Boom De Ay!
Men's schemes gang aft agley.
Let's cube our life away.
She: Long pause (having been here before):
-----------------------OY VAY!
I had the pleasure of meeting Shannon this summer when he came to visit when he was in England.
39
THE XL-25
At the London Toy Fair in 1983, Vulcan Electronics (previously known as the importer of the Hungarian Rings (C2-12 & C5/6-9/10)) displayed a new Hungarian electronic puzzle which has an interesting mathematical theory. The XL25 has a 5 × 5 (henceforth denoted 52 in our usual convention) array of buttons with lights behind them so the buttons appear either dark or lit up, starting with all buttons off, pressing a button lights up a pattern of squares. A second press of the same button turns off the same squares. If you press two buttons, both their patterns light up, except that any square which lies in both patterns is first lit up and then turned off. That is, a press of a button reverses all the lights in its pattern. We can phrase this a different way. Each light is affected by a certain pattern of buttons. If these buttons have been pressed an odd number of times, the light will be on, otherwise it is off.
 The XL25 has a choice of two patterns as shown on the right. The cross is five squares in the shape of a cross or +, affected by its central square. The knight is 9 squares comprising the button pressed and the 8 squares which are a knight's move away from it. If one is near an edge of the puzzle, the parts of the pattern which go over the edge are lost - they do not re-enter on the opposite side.
The XL25 has a choice of two patterns as shown on the right. The cross is five squares in the shape of a cross or +, affected by its central square. The knight is 9 squares comprising the button pressed and the 8 squares which are a knight's move away from it. If one is near an edge of the puzzle, the parts of the pattern which go over the edge are lost - they do not re-enter on the opposite side.
After some contemplation, the following structure becomes apparent. Consider the 25 squares as a list or vector of 25 values, where each value is either 0 (for off) or 1 (for on). A particular state of lights is thus a list or vector of 25 0s or 1s. The effect of pressing a button is also such a list and its effect on a given state is the sum of these two vectors, where we mean that we add the corresponding entries and this sum is done (mod 2) which means that 1+1 = 0. (This means that we are just doing the addition of odds and evens: even + even a even corresponds to 0 + 0 = 0; odd + even = odd corresponds to 1 + 0 = 1; odd + odd = even corresponds to 1 + 1 = 0.) The effect of pressing a set of buttons is then the sum of the effects of their individual effects.
This structure is precisely the multiplication of a matrix times a vector, where the arithmetic is done (mod 2) as just described. We now formalise this.
A play of the game is a 25-vector x = (x1, x2, ..., x25) where:
xi=1 if the i-th button is pressed (or is pressed an odd number of times);
xi=0 if the i-th button is not pressed (or is pressed an even number of times).
The state of the game is another 25-vector b, where:
bi=1 if the i-th light is on; bi = 0 if the i-th light is off.
Consider the effect of playing the j-th button when all lights are off. This produces a state which is a 25-vector, which is best considered as a column rather than a row, but it is too difficult to type columns, so I will say the state is (a1j, a2j, ..., a25,j) where aij = 1 if the j-th button affects the i-th light; = 0 otherwise. Then the pattern or state b produced by the play x, starting from the all off state is given by bi. = ∑j=1 aij xj (mod 2 as always). If we consider b and x as column vectors and let A be the matrix whose i,j entry is ai,j then this is the matrix product: b = Ax. I write this out in full below.
40

If x is played from some initial state c, then the result is b = Ax + c. The general problem of the XL25 is: given that you are in state c and want to get to state b, what must you play? This now can be phrased as; given c and b, find x such that b = Ax + c, i.e. such that Ax = b-c. This is the same as getting to the pattern b-c from the initial pattern of all offs. Thus we only need to consider starting from this pattern, which we denote by 0 = (0, 0, ... , 0).
Solving Ax = b is one of the classic techniques of mathematics and there are many methods available, of which the simplest is direct step by step elimination. However, this takes a lot of work (something like 5000 operations), so I wrote a program to do it on my Sinclair ZX81.
Knight pattern. For 22 up through 52, the matrix A is invertible and one can write down A such that AA-1 is the identity, so that Ax = b if and only if x = A-1b. Thus each b has a unique x which produces it. For example, for the 52, one can light the whole board from 0 in 17 moves, pressing all the buttons except the 8 which are adjacent to the corners. If one applies this to a pattern, the result is to form the complement of the pattern.
In fact, there are only 6 types of single location on a 52 (just as there are only six types of piece on a 53 - see C3/4-19). If we number the board as shown at the right, these are the locations 1, 2, 3, 7, 8, 13. Single squares of each type are lit by the following sets of buttons:
1 - 1,2,5,6,8,9,12,17,20,21,24 (11 moves)
2 - 1,4,7,9,10,11,12,13,15,16,17,18,20,23,24,25 (16 moves)
3 - 3,6,7,9,10,11,15,16,20,22,24 (11 moves)
7 - 2,3,4,5,6,7,10,11,14,16,18,21,22 (13 moves)
8 - 1,5,6,8,10,17,19,22,24 (9 moves)
13 - 2,4,6,10,13,16,20,22,24 (9 moves)
I illustrate the last pattern on the right. This has the remarkable feature that to light the central square, we press it and then press the other 8 squares that it lights up! These diagrams allow you to solve any problem. However, do not use them to light up one square at a time -this would use 313 moves to light up the whole board instead of the 17 described above. Instead, you should superimpose the diagrams for the squares which need to be lit and only press those buttons which occur an odd number of times.
41
Since each pattern has a unique play which produces it, there are 225 = 335 54432 patterns and the average number of moves per play is 25/2 = 12 1/2.
Cross pattern. The behaviour for this pattern turns out to be more interesting. For the 22 and 32 boards, the matrix A is invertible. But on the 42 and 52 boards, it is not. The degree of invertibility for an n by n matrix A is the rank of A, which is n if and only if A is invertible. The rank is the number of independent rows of A and we denote it by r. Then n-r is the number of conditions which each vector Ax must satisfy, and Ax = b is solvable if and only if b satisfies these n-r conditions, and then the solutions form a set of dimension n-r, which in our situation means a set of 2n-r elements.
For the 42 board, the matrix has rank 12 and no single square can be lit!
For the 52, the matrix has rank 23. A vector b can be of the form Ax if and only if it satisfies ∑bidi = 0, where d is one of the following to vectors, d, e:
d = (01110 10101 11011 10101 01110)
e = (10101 10101 00000 10101 10101).
From this we see that only the points i where di = ei = 0 can be obtained as singly lit squares - namely 7, 9, 13, 17, 19. There are 223 = 83 88608 patterns which can be obtained from 0 (or from any given starting point) and each obtainable pattern has 22 = 4 solutions.
Although we cannot invert the full 25 by 25 matrix A, one can obtain a pseudo-inverse of it. Our two dependence relations expressed by d and e can be viewed as determining the values of squares 24 and 25 in terms of the values of the first 23 squares. If these conditions are satisfied, we need only consider the first 23 entries of a vector and the corresponding 23 by 23 matrix. This is invertible and applying its inverse to the first 23 entries of b yields a solution x using only the first 23 buttons. If b satisfies our two conditions, then its last two entries must agree with the last two entries of Ax, where x has been extended to 25 entries by adding two 0 entries at the end. If one wants to get the same pattern, using buttons 24 and/or 25, one adds d and/or e to x. (This last result is not true for any matrix A - it depends on A being a symmetric matrix, as it is in our problems.)
From d and e, we can see that lighting just square 1 of the first 23 requires us to also light square 25. This is because d1 = 0, e1 = 1.
Similarly, square 2 implies we must light square 24, while square 3 requires 24 and 25. Let us classify the squares according to which configuration of di and ei or of 24 and 25 they involve.
| Case | di | ei | 24 | 25 | Squares |
| 0 | 0 | 0 | 0 | 0 | 7, 9, 13, 17, 19 |
| 1 | 0 | 1 | 0 | 1 | 1, 5, 21, 25 |
| 2 | 1 | 0 | 1 | 0 | 2, 4, 11, 12, 14, 15, 22, 24 |
| 3 | 1 | 1 | 1 | 1 | 3, 6, 8, 10, 16, 18, 20, 23 |
 These groups are shown on the board at the right. We now examine the effects of single buttons on these groups. Because of symmetry, there are just 9 types of button to consider 1, 2, 3, 6, 7, 8, 11, 12, 13. We denote the effect on groups 0, 1, 2, 3 by a quadruple a0, a1, a2, a3, where ai = 1 if an odd number of group i squares are affected; = 0 otherwise. Then the effects are as follows.
These groups are shown on the board at the right. We now examine the effects of single buttons on these groups. Because of symmetry, there are just 9 types of button to consider 1, 2, 3, 6, 7, 8, 11, 12, 13. We denote the effect on groups 0, 1, 2, 3 by a quadruple a0, a1, a2, a3, where ai = 1 if an odd number of group i squares are affected; = 0 otherwise. Then the effects are as follows.
42
| Buttons | Effect |
| 1 | 0, 1, 1, 1 |
| 2, 6 | 1, 1, 1, 1 |
| 3, 11 | 0, 0, 0, 0 |
| 7, 8, 12, 13 | 1, 0, 0, 0 |
Hence we see that the effect of one button is always of the form a, b, b, b, so the effect of any play must also be of this form. Thus any obtainable pattern (starting from 2) must have the parities of the numbers of lights in groups 1, 2, 3 all equal. Thus only 1/4 of the possible patterns can be achieved. This gives us an elementary approach to the conditions obtained from the analysis of the matrix A, but it doesn't show that all the permissible patterns can actually be achieved, which the pseudo-inverse does show.
Robert Stein, the proprietor of Vulcan Electronics, kindly sent my comments on to the inventor, Laszlo Meero. Meero replied that he had obtained similar results, but not using the pseudo-inverse. As we have seen, each achievable state using the cross has four solutions. Meero has shown that each such state can be achieved in at most 15 moves.
Meero also considers the general problems of n buttons with each button affecting some lights. As before, we set up an n by n matrix A with aij = 1 if the j-th button affects the i-th light; = 0 otherwise. Meero says that A is solvable if we can turn on all lights, starting from 0, i.e. all lights off. He has shown that if A is symmetric (aij = aji) and reflexive (aii = 1), then A is solvable. I managed to prove this also, but I have not tried to verify the following results.
Meero has studied the cross pattern problem on the n2 board and he finds that A is invertible for the following:
n = 1, 2, 3, 6, 7, 8, 10, 12, 13, 15, 18, 20, 21, 22, 25, 26, 27, 28, 31, 36, 37, 38, 40, 42, 43, 45, 46, 48, 51, 52, 55, 56, 57, 58, 60, 63, 66, 68, 70, 72, 73, 75, 76, 78, 80, 81, 82, 85, 86, 87, 88, 90, 91, 93, 96, 97, 100. (57 values up through 100.)
These do not exhibit an obvious pattern! He has shown that A is invertible infinitely often and is non-invertible infinitely often and that the non-invertible cases have positive lower density. (I.e. the number of them up through x is bigger than some positive multiple of x for all large x.) A friend of Meero has studied fixed points in the same problem. A fixed point x is a play which lights up just the buttons of x, i.e. it is a solution of x = Ax. He finds that there are 2n of these. (The phrasing isn't clear if there may be more.) He also studies anti-fixed points, which are plays which light up the complement of the buttons pressed. For n even, there are 2n of these, while for n odd, there are none.
The knight pattern on the n2 has an invertible matrix if n != 6, 7, 8 (mod 9). (I.e. if n is not of the form 9a + 6, 7, 8.) I find this an intriguing assertion and I have not yet seen why this should hold. Meero says the 72 is a hard problem.
Meero has also studied buttons with three states, but his description is too sketchy to reproduce here. Buttons with four states will lead to interesting ? complications since the arithmetic (mod 4) no longer has division and so the standard methods for solving matrices break down and must be replaced by more complex methods.
Clearly there are some interesting questions generated by this puzzle and some of the results sent by Meero are quite intriguing. Are there patterns such that A is invertible for all n? (Obviously the one button per light patterns are always invertible, but are pretty trivial.)
What happens if we think of our board as toroidal - i.e. if a play goes off an edge, it comes back in the opposite edge?
43
CURIOUS CUBIC CORRESPONDENCE
I have received a number of amusing letters. I reproduce them below, but the names have been deleted to protect the innocent!
Dear Sirs(o):
I am inquiring into the cube. I'm find my mistakes to be in the adaptation "of the cube" to the primary purpose of which it should have achieved. Please respect.
(This one came from Florida and was addressed to my Department.)
Dear Sir
I was a full time Ph.D. Student in Computer Science until I discovered the "Magic Cube" (please include my name in the list of possible candidates for your television advertisement) which has converted me to a full time Student in Group Theory (a subject I very much hated in my under-graduate days) and part time Student in Computer Science.
To ease our suffering (another two Ph.D. Students who have also become part timers) please send us 3 copies of ...
Dear Sir,
My name is ... and I live in (Italy). Some time ago I bought the excitant puzzle invented of the now famous engineer Ernő Rubik; I am talking about the cube wich from several time is doing to become insane the west. Is for avoid of be involved in the exasperated multitude who I write it, and I enclose 3 U. 5. dollars for receive his book: "Notes on the Magic Cube". I thank you in advance for your collaboration and I beg you to accept my more friendly regards.
Dear Mr Singmaster,
Recently a friend of mine acquired a Magic Cube through ... from you. Since I first played with the cube I have become a nervous wreck, failed my finals and torn out a large proportion of my hair. They say it is because I did Physics that I haven't cracked the problem yet - but I'll show them I'm not that stupid. The trouble is, our term will soon be ending (a fortnight in fact) and then I'll be cubeless.
Please would you help to keep up your record and not only ruin my degree but also get me the sack from my new job. I'll tell you something else - I'm a sadist - so I would appreciate it if you would help to ruin two other lives, those of my brother and a friend.
You can do all this by sending me three Magic Cubes ...
Mr. David Singmaster
I am any one more many amateur to the "Rubik's Cube", of whom frigthen me his utility for Maths. I am studying Maths.
Thoug, still I haven't some deeps acquaintances about "cube" I pretend to profite the best of his possibilitys.
Then, I would like acquire yours "NOTES ON RUBIK' MAGIC CUBE" and, I am sure, they will be for me very usefuls.
I secure you my cooperation in all that think can be of your interest.
I will await your notices with impatience. Thank you very much.
Mr Singmaster,
My name is ... I am a student of .., at ... I read in our newspaper a text about yours book "NOTES ON RUBICS MAGIC CUBE". I am very interested on it as a long time (about 18 months) I tried and successed to make it well. I can do it (cube) for a one till two minutes. I know a several systems. In our newspapers I found many texts about magic cube, but I didn't learn any new thing from them.
I would like to read your book in originale because I can't bye it in Yugoslavia. Translate of your book is not done yet, and it wouldn't be soon. So, I would like to have your book, and I beg you to send me one copy of it. if you can't send me a book, please send me some texts about magic cube.
I am sorry of my bad English but I think that you will understand this letter.
Thanks in advice.
44
One of the shortest letters received was the following.
Thank-you David
Thank-you David
Thank-you David
Sir:
Here is your dollar extra ...
I strongly suggest you apply for sainthood - your notes have finally made me the cube's master and not the other way around: I Thank you.
The well known science fiction writer Arthur C. Clarke wrote from Sri Lanka, asking for a copy of the Notes, which was duly sent. He sent a card of acknowledgement.
Dear Cubemeister Singmaster,
Thanks for the booklet, I hope to spread the plague in Sri Lanka as soon as I get back.
Meanwhile I wonder what the record time is for the coward's way out, with screwdriver...
William W. Erdis, of County Antrim, couched his request in verse.
Dear Sir,
Oh please your book you must send
This Cube I've got has me round the bend,
I can do face's and crosses.
But all side faces has me at losses.
At the top of the page my address you'll see,
I will be ever so grateful
If you will send to me.
THE NOTES ON RUBIC'S MAGIC CUBE
(Mr. Erdis's typing is a bit erratic - the end of the fourth line is at lost,es which might also be rendered at loss, yes ??)
The following letter is perhaps the most startling and amazing that I received. Among other things it was dated 30 November 1981 and we received it on the 14 November 1981! Part was written in red ink and some parts were doubly written in red and blue. I will underline the red material and enclose the double coloured material in *s.
APPLICATION.
I AM IN TROUBLE
Dear Sir, David.
Your RUBIK'S MAGIC CUBE how it has surprise many people only God knows.
Is that when I read the book and I esplaned to them. About 200 people was'ent believe it at all, only 2 people believe it. *I also believe it.* I am a young boy of 20 years. How I told people.
45
I went to our Chief here, and told him what I have read, and said I'd like people also to hear it, and he gave me a Note. I finish only *30 minuts*, When I finished, the chief called the people. After meeting they told me this: Young boy, you have waist our time and so write to David Singmaster and ask him Rubik's Magic Cube. IF he gave it to you then it's true story but IF he did'nt gave it to you, please you'll be in prison. They have given me only 4 (FOUR) months. If four months, I did'nt have I will be in trouble. Please because of your wonderfull thing am in trouble.
Sir, all the thing I have said to you. Give me, to show them, so that I will set Free they are worry me too much mm! mm! mm!
Thank you for your co-opration and attention I remain
Yours faithful
(The author's writing is occasionally hard to decipher, but I think I've managed. Needless to say, I sent him a copy of the book and a letter and some other material, but it was not clear to me if his people did not believe in the existence of the cube or in the solution method. I never had a reply - I hope he's all right!)
A 43 COMPETITION
I have only heard of one Rubik's Revenge (= 43) Competition. This was organised by the Daily Star, a UK newspaper, on 25 June 1983. Julian Chilvers, the UK Rubik's Cube Champion, was best with a time of 119 sec. He won a Ford Fiesta 950 painted all over with cubes. Unfortunately, he's too young to drive and so he sold it.
1000DM IN PRIZES
In his German book, Christoph Bandelow offered 1000DM (= £263 = $368) in prizes for the best process for forming the Superfliptwist pattern. This has all edges flipped in place and all corners twisted in place, with adjacent corners having opposite twists. Thus the corners with positive twist form a regular tetrahedron. The winning solution came from Rainer aus dem Spring of Oberhausen.
UFs2Rs2U'.L'U2Fs'L2U'F'B'U2L'FsRs'F2B (22)
The contest was dropped from the English edition, but Bandelow has said he will give some prize for any improvement on this. This is thought to be a likely candidate for a most difficult position to achieve. I cannot readily see if this is a local maximum in Hoey and Saxe's theory, and I cannot see that my argument on C5/6-24 works. Wait, I think it does work - the symmetries which preserve the tetrahedron of positively twisted corners is certainly enough to take any face to any other, and the mirror image of the pattern is again itself, so we also get all the inverses of faces. So the argument is the same as for the 12-flip and the superfliptwist should be a local maximum.
A CUBIC SICK JOKE
What goes 'Click-click - have I done it?'
A blind man doing the Rubik Cube.
From: Michael Kilgarriff. Oh No! Not Another 1000 Jokes for Kids. Ward Lock, London, 1983.
46
RUBIK'S FOUNDATION
Hungarian Exporter 33:9 (Sep 1983) 7-8 gives the moat detailed account of the founding of the Rubik Innovation Foundation. Rubik has contributed 7 million forints to establish a foundation to assist Hungarians in 'the practical realization of innovative ideas'. Since the forint is a controlled currency, it is a bit difficult to translate it into western amounts, but I recall rates of about 70 forints to the pound a few years ago. (I've just rung the Hungarian Embassy and they say it is currently 62 forints to the pound.
YOUNGEST CUBIST?
M. Antony, of Cochin, India, reports that his daughter, then 5 years, 1 month and 11 days old, can do the cube from any position in under three minutes. This is certainly the youngest genuine solver that I know of. (But compare C2-4 and C5/6-4.)
CUBIC MAIL BOX
Michael van der Riet has built a cubical post box in front of his house in Bellville, South Africa.
RUBIK CUBIK MAGIK
Magicians may be interested in a book with this title, by Kennedy Smith, published by Kanda Publications, Falkirk, 1982. It gives Ii magic tricks using the Cube as a prop. You will probably have to get it at a magic shop - I got mine at Davenport's, Charing Cross Underground Arcade, London.
A NOVEL APPEARANCE
Alastair Shepherd has found a novel entitled "Rubik's Cube". It is by Leela Dutt and was published by Gee & Son, Ltd., Denbigh, Clwyd, Wales, 1984. The back cover blurb says it's about Cruise missiles in South Wales - "like the squares on Rubik's cube, the pattern gets muddled". On p. 13, we find the following passage.
"... Oh, by the way - she gave him one of those Rubik's cubes yesterday."
"What's that? Oh, I know, my kids used to have one."
"You don't see them about so much now, but there was quite a craze for them in the early eighties - do you remember? My two were too small to do it."
"Yes, I remember. I could never work out what you were supposed to do with the darn thing."
"It was lovely when he first brought it home - all smooth and shiny, with all the colours in the right place. Just right. The trouble is, as soon as you give it a few twists, it all gets muddled up and you can't get back to where you were."
"I always thought they were rather boring. I suppose you have to have that sort of mind...."
47
THE HISTORY AND FURTHER TRIALS OF THE CUBE
In C5/6-23/24, I discussed the prehistory of the cube. I have now seen William G. Gustafson's US Patent 3,081,089 of 12 March 1963 for a 'Manipulatable Toy'. This is a spherical 23. The construction is basically a grooved sphere, with pieces sliding on it. However, his first version is unsymmetric in that the spherical-triangular pieces have a lip only at one corner. The eight lips meet in fours at two antipodal groove crossings and reach in under the groove edges to provide the holding mechanism. It is difficult to see that this does give a fully moveable cube or sphere. It does seem that this is a rather loose mechanism and he gives a second, symmetric, version where each piece has lips at all three corners. Gustafson's pieces do not abut edge to edge - one can see the interior sphere between any two adjacent pieces. Consequently one can relate the exterior pattern to the inner sphere and this gives 24 times as many overall patterns as for an ordinary 23. Interestingly, he does not attach any piece to the central sphere - instead he has detents to let you align the pieces with the grooves on the central sphere. It may be that the need to do this required the interior sphere to be visible.
The suit described in C5/6-23/24 went to trial in late January 1984 in Wilmington, Delaware. Jerry Slocum, the world's leading puzzle collector, was an expert witness for Moleculon for four days of the nine days of the trial. In his opinion, the cubical shape with coloured faces was a major advance over Gustafson's patent. Gustafson has admitted that he had not realised the puzzle aspects of his device. Further, Slocum's study of the patent and puzzle literature revealed no other 'prior art' for this sort of puzzle. Although it now seems obvious to go from the sphere to the cube, neither Gustafson nor anyone else had done so prior to Nichols. Consequently the court ruled, on 2 October 1984, that Nichols' patent was valid and that Ideal (since taken over by CBS) had infringed on that patent.
However, the story is not yet over. The court must assess what damages to award to Moleculon. There is no doubt that Nichols did not have an effective mechanism. His magnets make it too easy to cheat. This may have been a factor in the universal rejection of his device by the toy trade when Moleculon tried to sell it in the early 1970s. (I have also heard that Gustafson tried to market his sphere and was rejected by 80 companies.) All parties are agreed that Rubik's invention was independent. I cannot see that anyone can doubt that Rubik's mechanism represents a major improvement over Nichols' patent and hence it deserves the major credit for the success of the Rubik Cube. In view of this, I would predict that the court will award only a small fraction of the damages sought.
As I have said, the mechanism is the most wonderful part of the Cube. I, and most other people, will continue to acknowledge this by continuing to call it Rubik's Cube.
A RUMOUR
Douglas Hofstadter told me about two years ago that he had heard a rumour
that a Princeton undergraduate had shown that God's Algorithm for the 33
had maximum length 26. However, I've heard nothing more of it, so it seems
unlikely.
48
SOME PYRAMINX VARIATIONS
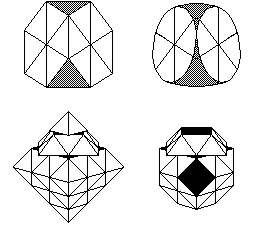 Mèffert made an octahedral version of the Pyraminx, but only in sample quantities. It is shown of the lower left. Several other versions appeared, even in Poland!
Mèffert made an octahedral version of the Pyraminx, but only in sample quantities. It is shown of the lower left. Several other versions appeared, even in Poland!
The first truncated Pyraminx was a crude version made in Canada by Rubin's Toy Company.
The second version looks like a sphere cut by three tangent circles. It came from Taiwan. The truncated octahedron also came from Taiwan. It is a pleasant shape, especially when sitting on a hexagonal face.
A MAD COMMENT
The UK edition of Mad Magazine for November 1984 ha a cartoon showing a Boob Cube (C3/4-9) in a feature on 'Simple Games and Pastimes for the School Drop-Out.' The cartoon is labelled somewhat obscurely 'Two-colour Rubik Cubes'.
© David Singmaster
The text and original drawings are copyright © David Singmaster, reproduced here with
permission. Conversion to html and additional commentary by Jaap Scherphuis.
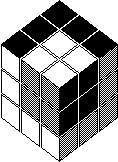
 When I was in Poland in 1983, I accidentally found a shop with four shapes of cube that I have never seen elsewhere. These were labelled Original Toys, Poland. The first was the twisted octagonal prism shown on the right. This has two areas interlocked like the halves of a tennis ball or baseball. These two areas are solidly coloured giving a peculiar two-coloured object. I have shaded one of the areas in the figure.
When I was in Poland in 1983, I accidentally found a shop with four shapes of cube that I have never seen elsewhere. These were labelled Original Toys, Poland. The first was the twisted octagonal prism shown on the right. This has two areas interlocked like the halves of a tennis ball or baseball. These two areas are solidly coloured giving a peculiar two-coloured object. I have shaded one of the areas in the figure. It has twelve rhombic faces whose acute angles meet at four fold vertices and whose obtuse angles meet at three fold vertices. The rhombuses correspond to the edges of a cube or octahedron, The rhombic dodecahedron is the shape obtained by trimming a cube to octagonal cross sections along all three axes, then peaking all the face centres to square pyramids. Alternatively, if you take a geometric cube and cut it by 45° planes along all edges, the result is the rhombic dodecahedron. The third Polish Cube was a proper rhombic dodecahedron, with 12 colours. I find this a most elegant shape. It is actually equivalent to Mondadori's Master Cube (
It has twelve rhombic faces whose acute angles meet at four fold vertices and whose obtuse angles meet at three fold vertices. The rhombuses correspond to the edges of a cube or octahedron, The rhombic dodecahedron is the shape obtained by trimming a cube to octagonal cross sections along all three axes, then peaking all the face centres to square pyramids. Alternatively, if you take a geometric cube and cut it by 45° planes along all edges, the result is the rhombic dodecahedron. The third Polish Cube was a proper rhombic dodecahedron, with 12 colours. I find this a most elegant shape. It is actually equivalent to Mondadori's Master Cube ( The East German firm VEB Spielvaren, in Pfaffschwende, is currently producing a series of four variations on the 23. The simplest is just an octahedron formed by truncating the corners of the 23, Each face has three coloured spots, one at each corner, so this is really the same as the six-colouring of the cube. If one puts regular tetrahedra on all eight faces of the octahedron, the result is the Stella Octangula discovered by Kepler. One can view it as two large interpenetrating tetrahedra or as one large tetrahedron with small tetrahedra on the centre of each face. It is four coloured in accordance with this last description - a large face and the small tetrahedron on it are of one colour,
The East German firm VEB Spielvaren, in Pfaffschwende, is currently producing a series of four variations on the 23. The simplest is just an octahedron formed by truncating the corners of the 23, Each face has three coloured spots, one at each corner, so this is really the same as the six-colouring of the cube. If one puts regular tetrahedra on all eight faces of the octahedron, the result is the Stella Octangula discovered by Kepler. One can view it as two large interpenetrating tetrahedra or as one large tetrahedron with small tetrahedra on the centre of each face. It is four coloured in accordance with this last description - a large face and the small tetrahedron on it are of one colour,
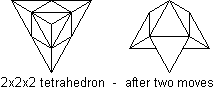 This 2 × 2 × 2 tetrahedron was invented by several people, including Rubik and Barry Lockwood of Rochdale.
This 2 × 2 × 2 tetrahedron was invented by several people, including Rubik and Barry Lockwood of Rochdale.
 RAINBOW PATTERNS
RAINBOW PATTERNS A more interesting variant has recently been given to me by Alistair Shepherd. He is a haematologist with the Blood Transfusion Service in Liverpool, which produces a small circular sticker showing two adjacent hearts, He has replaced all the coloured stickers on a cube with these, in such a way that each face has all the stickers oriented in the same way. A view is shown in the adjacent figure, where the direction of the hearts is shown by the arrows. Opposite faces have opposite orientations.
A more interesting variant has recently been given to me by Alistair Shepherd. He is a haematologist with the Blood Transfusion Service in Liverpool, which produces a small circular sticker showing two adjacent hearts, He has replaced all the coloured stickers on a cube with these, in such a way that each face has all the stickers oriented in the same way. A view is shown in the adjacent figure, where the direction of the hearts is shown by the arrows. Opposite faces have opposite orientations. First, one needs further notation. The following is rather ad-hoc for this particular problem and may not be optimal for other problems. We adopt a numerical coordinate system for cubelets. The cubelet (x, y, z) will be in layer x from the R face (so the R face has x = 1), layer y from the F face and layer z from the U face. Then (1, 1, 1) or (111) or 111 denotes the RFU corner which is in the centre of our usual diagram. The case n = 6 is shown on the right with cubelet 111 marked out. I will denote turns as R1, R2, R3, ... meaning to turn the layer x = 1, 2, 3... 90° clockwise as viewed from the R face. Now let a = n+1-a denote the complement of a. Note that 111 is the mirror image of 111 in the midplane of the cube which is parallel to the R face, i.e. the plane given by x = (n+1)/2. On the 33, 111 is LUF.
First, one needs further notation. The following is rather ad-hoc for this particular problem and may not be optimal for other problems. We adopt a numerical coordinate system for cubelets. The cubelet (x, y, z) will be in layer x from the R face (so the R face has x = 1), layer y from the F face and layer z from the U face. Then (1, 1, 1) or (111) or 111 denotes the RFU corner which is in the centre of our usual diagram. The case n = 6 is shown on the right with cubelet 111 marked out. I will denote turns as R1, R2, R3, ... meaning to turn the layer x = 1, 2, 3... 90° clockwise as viewed from the R face. Now let a = n+1-a denote the complement of a. Note that 111 is the mirror image of 111 in the midplane of the cube which is parallel to the R face, i.e. the plane given by x = (n+1)/2. On the 33, 111 is LUF.

 Now that a 53 has been made, people often ask about 63, etc. I was told that these were impossible as the corners would fall off as face turned. However, upon checking, this does not actually happen until n = 7, If we assume the cubies have edge 2, then the distance from the face-centre O to the edge of the cube is n and the distance from O to the inner corner P of a corner piece is x = (n-2)√2. So the corner will fall off as it turns if x > n, i.e. (n-2)√2 > n. This easily gives n > 2√2/(√2 - 1) = 4 + 2√2 = 6.8+. So a 63 is technically possible with cubical cubies, but a 73 is not. One can get around this by making the outer layers thicker than the inner layers, as with Trajber's octahedron (
Now that a 53 has been made, people often ask about 63, etc. I was told that these were impossible as the corners would fall off as face turned. However, upon checking, this does not actually happen until n = 7, If we assume the cubies have edge 2, then the distance from the face-centre O to the edge of the cube is n and the distance from O to the inner corner P of a corner piece is x = (n-2)√2. So the corner will fall off as it turns if x > n, i.e. (n-2)√2 > n. This easily gives n > 2√2/(√2 - 1) = 4 + 2√2 = 6.8+. So a 63 is technically possible with cubical cubies, but a 73 is not. One can get around this by making the outer layers thicker than the inner layers, as with Trajber's octahedron ( As usual, we first need some notation. We refer to the eight corners as URF, etc. and the six centres as U, R, F, D, L, B. Since a move is most easily described as the turning of a corner, it is convenient to have simple names for the corners. I use the numbers 1 to 8 as shown in the adjacent figure. (Corner 7 is the hidden LDB corner.) Then the move 1 means the turn of the half cube centred on corner 1 by 120° clockwise, as viewed from the outside. I also use 1+, 1- for the action of a move when corner 1 is rotated in its place.
As usual, we first need some notation. We refer to the eight corners as URF, etc. and the six centres as U, R, F, D, L, B. Since a move is most easily described as the turning of a corner, it is convenient to have simple names for the corners. I use the numbers 1 to 8 as shown in the adjacent figure. (Corner 7 is the hidden LDB corner.) Then the move 1 means the turn of the half cube centred on corner 1 by 120° clockwise, as viewed from the outside. I also use 1+, 1- for the action of a move when corner 1 is rotated in its place. To restore the Skewb, we can proceed as follows.
To restore the Skewb, we can proceed as follows.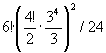 .
That is, the centres can be in any permutation and each tetrad can have its corners in any even permutation and twisted so the total twist is 0 (mod 3), but the whole cube has 24 equivalent placements.
.
That is, the centres can be in any permutation and each tetrad can have its corners in any even permutation and twisted so the total twist is 0 (mod 3), but the whole cube has 24 equivalent placements.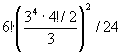 .
Incidentally, the odd permutations of the centres correspond to movements of the whole cube which interchange the tetrads. If we do not allow the tetrads to be interchanged, then both the 6! and the 24 are divided by 2.
.
Incidentally, the odd permutations of the centres correspond to movements of the whole cube which interchange the tetrads. If we do not allow the tetrads to be interchanged, then both the 6! and the 24 are divided by 2. You may have seen some of the different ways of joining pieces. The most common method for cardboard pieces is the use of 'ears' along the edges as shown in Figures 1 - 3. The ears are folded and then joined by a rubber band over them. This idea was patented by Fred Bassetti, an architect from Portland, Oregon,
You may have seen some of the different ways of joining pieces. The most common method for cardboard pieces is the use of 'ears' along the edges as shown in Figures 1 - 3. The ears are folded and then joined by a rubber band over them. This idea was patented by Fred Bassetti, an architect from Portland, Oregon, 

 I have seen a number of other methods of joining cardboard polygons, using tabs and slots, but I do not find them easy to use - either they come apart too easily or they don't come apart at all. Joining plastic pieces along a hinged edge is not as easy and I had only noted one attempt to do this before this year, though there may have been others I didn't know about. The object I had first seen was the Happy Cubes made by the US firm of Mag-Nif and unfortunately not available in the UK. This had eight cubes joined in a chain by the edge connection shown at the right1 Figure 14. Unfortunately, the plastic was a bit soft and the outer parts of the hinge were too rigid, so that the balls which fit in the sockets soon wore down and the puzzle would fall apart when you picked it up.
I have seen a number of other methods of joining cardboard polygons, using tabs and slots, but I do not find them easy to use - either they come apart too easily or they don't come apart at all. Joining plastic pieces along a hinged edge is not as easy and I had only noted one attempt to do this before this year, though there may have been others I didn't know about. The object I had first seen was the Happy Cubes made by the US firm of Mag-Nif and unfortunately not available in the UK. This had eight cubes joined in a chain by the edge connection shown at the right1 Figure 14. Unfortunately, the plastic was a bit soft and the outer parts of the hinge were too rigid, so that the balls which fit in the sockets soon wore down and the puzzle would fall apart when you picked it up.
 More recently, I have seen the Tri Logic of Mag-Nif. This has 24 triangles in plastic with hinges as shown on the right, Figure 5. Each edge has two of the hinges, one male part and one female part on each side of the edge. I haven't had mine long enough to see how sturdy it is. It does have the obvious disadvantage that they have tried to bring the edges to a real meeting point and this produces an extremely sharp point at each vertex.
More recently, I have seen the Tri Logic of Mag-Nif. This has 24 triangles in plastic with hinges as shown on the right, Figure 5. Each edge has two of the hinges, one male part and one female part on each side of the edge. I haven't had mine long enough to see how sturdy it is. It does have the obvious disadvantage that they have tried to bring the edges to a real meeting point and this produces an extremely sharp point at each vertex.
 Another version of idea is Clixi, produced by ESA Creative Learning, Harlow, UK. Their joint is shown on the right, Figure 6. Again each edge has two of the hinges, with one of each sex on each side. Clixi also provides squares, pentagons, circles and some cross pieces. The squares (at least) have joints moulded into the inside so that one can attach a piece to the interior of the square. This, and the circles and cross pieces, make this a much more general construction kit than the other kits described here. A 140 page booklet, 'Exploring Mathematics with 'Clixi', comes with it and is obviously aimed at 8-12 year olds. The corners are better rounded than in Tri Logic, but the pieces are supplied in moulded sheets and do not detach cleanly.
Another version of idea is Clixi, produced by ESA Creative Learning, Harlow, UK. Their joint is shown on the right, Figure 6. Again each edge has two of the hinges, with one of each sex on each side. Clixi also provides squares, pentagons, circles and some cross pieces. The squares (at least) have joints moulded into the inside so that one can attach a piece to the interior of the square. This, and the circles and cross pieces, make this a much more general construction kit than the other kits described here. A 140 page booklet, 'Exploring Mathematics with 'Clixi', comes with it and is obviously aimed at 8-12 year olds. The corners are better rounded than in Tri Logic, but the pieces are supplied in moulded sheets and do not detach cleanly.
 The version that I saw at the Toy Fair this year seems to be definitely the nicest that I have seen. The hinge was devised by Edward Harvey and the pieces are being produced by Polydron UK, Unit 12, Staveley Way, Brixworth Industrial Estate, Brixworth, Northampton-shire, NN6 9EU, UK. The hinge is shown at right, Figure 7. Because of the intricacy, I have drawn only one side of the hinge. The other side is identical, just turned over. The pieces are thick and come in four primary colours with a smooth finish. The corners are neatly rounded.
The version that I saw at the Toy Fair this year seems to be definitely the nicest that I have seen. The hinge was devised by Edward Harvey and the pieces are being produced by Polydron UK, Unit 12, Staveley Way, Brixworth Industrial Estate, Brixworth, Northampton-shire, NN6 9EU, UK. The hinge is shown at right, Figure 7. Because of the intricacy, I have drawn only one side of the hinge. The other side is identical, just turned over. The pieces are thick and come in four primary colours with a smooth finish. The corners are neatly rounded.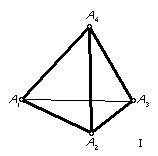
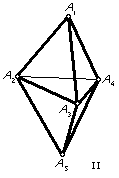
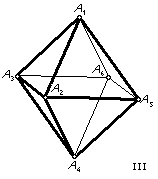
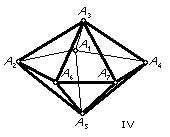
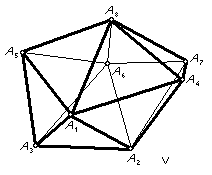
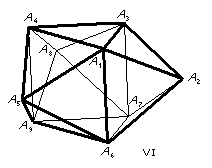
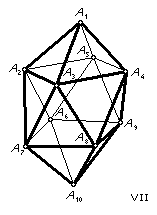
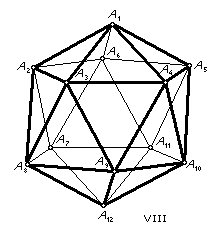
 I have drawn bits of the triangular and hexagonal lattices to the right since these are the least familiar of the above solutions. These figures are often denoted by the Schläfli symbol {p, q}. The figure {p, q) is dual to the figure {q, p} in that the roles of vertices and faces are interchanged. E.g. the octahedron has 6 vertices and 8 faces, while its dual, the cube, has 8 vertices and 6 faces. The easiest way to construct a dual is to take new vertices at the centres of the old faces and join these if the corresponding old faces are adjacent. I have bracketed the dual pairs in the table on the preceding page. Note that (3,3) and {4,4} are self-dual.
I have drawn bits of the triangular and hexagonal lattices to the right since these are the least familiar of the above solutions. These figures are often denoted by the Schläfli symbol {p, q}. The figure {p, q) is dual to the figure {q, p} in that the roles of vertices and faces are interchanged. E.g. the octahedron has 6 vertices and 8 faces, while its dual, the cube, has 8 vertices and 6 faces. The easiest way to construct a dual is to take new vertices at the centres of the old faces and join these if the corresponding old faces are adjacent. I have bracketed the dual pairs in the table on the preceding page. Note that (3,3) and {4,4} are self-dual. If we remove the condition that our figure is convex, we obtain Is further polyhedra called the Kepler-Poinsot polyhedra. The great dodecahedron is just the shape of Alexander's Star (
If we remove the condition that our figure is convex, we obtain Is further polyhedra called the Kepler-Poinsot polyhedra. The great dodecahedron is just the shape of Alexander's Star (



 Each of these is a mixture of two dual figures and can be viewed several ways. If we start with a cube and truncate its corners more and more until the triangles formed at the corners just touch, then we have the cuboctahedron. Truncating further leads to the octahedron. We can also truncate the octahedron to get the cuboctahedron and then the cube. We can see that the vertices of the cuboctahedron correspond to the edges of the cube (or octahedron) while the faces correspond to the faces and the vertices of the cube (or octahedron). We have p1F1 = p2F2 = E.
The icosidodecahedron is similarly the truncation of the dodecahedron or the icosahedron. The lattice of triangles and hexagons, shown on the right, can be viewed as a truncation of {3,6} or {6,3}, but it may be easier to see by taking the triangular or hexagonal lattice and placing new vertices in the centre of each edge and joining the vertices of adjacent edges, where adjacent means having a common vertex and a common face. These figures were certainly known to the Greeks. Archimedes, in a lost account, ascribes the cuboctahedron to Plato, and Archimedes describes the icosidodecahedron.
Each of these is a mixture of two dual figures and can be viewed several ways. If we start with a cube and truncate its corners more and more until the triangles formed at the corners just touch, then we have the cuboctahedron. Truncating further leads to the octahedron. We can also truncate the octahedron to get the cuboctahedron and then the cube. We can see that the vertices of the cuboctahedron correspond to the edges of the cube (or octahedron) while the faces correspond to the faces and the vertices of the cube (or octahedron). We have p1F1 = p2F2 = E.
The icosidodecahedron is similarly the truncation of the dodecahedron or the icosahedron. The lattice of triangles and hexagons, shown on the right, can be viewed as a truncation of {3,6} or {6,3}, but it may be easier to see by taking the triangular or hexagonal lattice and placing new vertices in the centre of each edge and joining the vertices of adjacent edges, where adjacent means having a common vertex and a common face. These figures were certainly known to the Greeks. Archimedes, in a lost account, ascribes the cuboctahedron to Plato, and Archimedes describes the icosidodecahedron. The duals of these figures are less obvious. They are figures with all faces and edges being the same and the vertices are regular. This means that the pattern of faces at a vertex forms a regular polygon. These are less easy to see and hence have not been investigated as much. The faces are all rhombuses, but with different angles. The polyhedral ones are the rhombic dodecahedron and the rhombic triacontahedron. The rhombic dodecahedron is described in
The duals of these figures are less obvious. They are figures with all faces and edges being the same and the vertices are regular. This means that the pattern of faces at a vertex forms a regular polygon. These are less easy to see and hence have not been investigated as much. The faces are all rhombuses, but with different angles. The polyhedral ones are the rhombic dodecahedron and the rhombic triacontahedron. The rhombic dodecahedron is described in 
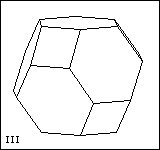
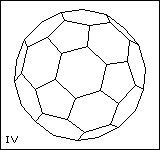
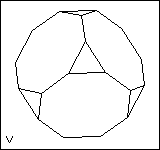
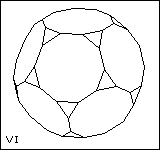
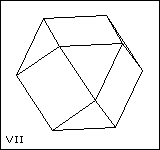
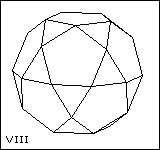
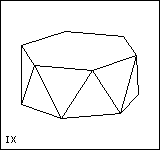
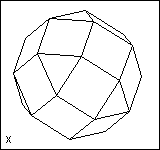
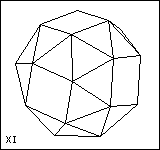
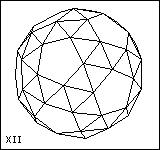
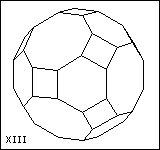
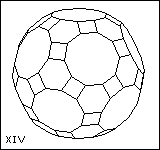
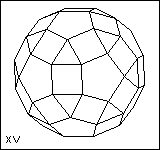



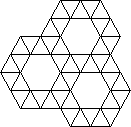
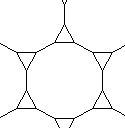
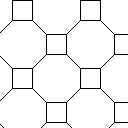


 The mechanism is quite intricate and fits together in two basic ways. The first diagram on the right shows the basic shape of the piece, although the actual pieces are hollow in the middle. The projecting teeth have cylindrical rods or hollows on them which provide the axis of rotation. There are two types of edge: male with rods projecting from the teeth and female with hollows in the teeth. These are shown in the diagrams below. Because of the alternating nature of the teeth, a male and a female can be joined in two ways.
The mechanism is quite intricate and fits together in two basic ways. The first diagram on the right shows the basic shape of the piece, although the actual pieces are hollow in the middle. The projecting teeth have cylindrical rods or hollows on them which provide the axis of rotation. There are two types of edge: male with rods projecting from the teeth and female with hollows in the teeth. These are shown in the diagrams below. Because of the alternating nature of the teeth, a male and a female can be joined in two ways.
 The more natural is the join of the first diagram on the left with the second one. Then the pieces can rotate about the cylindrical axis. The less obvious join is of the first diagram with the third one. Then the teeth overlap and form a rigid joint.
The more natural is the join of the first diagram on the left with the second one. Then the pieces can rotate about the cylindrical axis. The less obvious join is of the first diagram with the third one. Then the teeth overlap and form a rigid joint.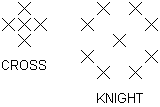 The XL25 has a choice of two patterns as shown on the right. The cross is five squares in the shape of a cross or +, affected by its central square. The knight is 9 squares comprising the button pressed and the 8 squares which are a knight's move away from it. If one is near an edge of the puzzle, the parts of the pattern which go over the edge are lost - they do not re-enter on the opposite side.
The XL25 has a choice of two patterns as shown on the right. The cross is five squares in the shape of a cross or +, affected by its central square. The knight is 9 squares comprising the button pressed and the 8 squares which are a knight's move away from it. If one is near an edge of the puzzle, the parts of the pattern which go over the edge are lost - they do not re-enter on the opposite side.



 These groups are shown on the board at the right. We now examine the effects of single buttons on these groups. Because of symmetry, there are just 9 types of button to consider 1, 2, 3, 6, 7, 8, 11, 12, 13. We denote the effect on groups 0, 1, 2, 3 by a quadruple a0, a1, a2, a3, where ai = 1 if an odd number of group i squares are affected; = 0 otherwise. Then the effects are as follows.
These groups are shown on the board at the right. We now examine the effects of single buttons on these groups. Because of symmetry, there are just 9 types of button to consider 1, 2, 3, 6, 7, 8, 11, 12, 13. We denote the effect on groups 0, 1, 2, 3 by a quadruple a0, a1, a2, a3, where ai = 1 if an odd number of group i squares are affected; = 0 otherwise. Then the effects are as follows. Mèffert made an octahedral version of the Pyraminx, but only in sample quantities. It is shown of the lower left. Several other versions appeared, even in Poland!
Mèffert made an octahedral version of the Pyraminx, but only in sample quantities. It is shown of the lower left. Several other versions appeared, even in Poland!