


Uriblock, also known as Mix Box, is a type of sliding piece puzzle. It consists of 16 tiles in a 4×4 square. Each row and each column has a slide which can move the 4 tiles in that row or column one square. The top row slide can only move to the right, one square (and then back again), the second row slide only to the left, the third to the right, and the bottom one only to the left. Similarly the columns can only move in alternate directions up and down. Note that this arrangement is symmetric - it looks just the same after a quarter turn of the puzzle. When a slide has been moved, part of the slide has entered the 4×4 area, and so blocks the movement of the nearest perpendicular slide.
The 16 tiles are coloured, four of each of the colours red, yellow, green, and blue. The aim is to arrange them in rows (or equivalently columns).
The puzzle is somewhat similar to the Rubik's Fifteen and Tsukuda's Square (a.k.a 'It'). Uriblock was invented by and named after Dario Uri. It was made in the mid eighties. It is mentioned in Cubic Circular Issue 7/8, p19.
If your browser supports JavaScript, then you can play Uriblock by clicking the link below:
Suppose the slides are in their original positions, so that the tiles form a square. There are 16 tiles, so there are at most 16! positions. This limit is not reached because there are 4 sets of 4 identical tiles. This gives 16! / 4!4 = 63,063,000 positions. It is impossible for all four of the outermost sliders to be in the pushed in state at the same time. 9Other than that, all slider positions are possible, so there are 24(24-1) = 240 slider positions. This gives a total of 15,135,120,000 positions. Note however that it does not matter what order the colours are in the solution. Therefore either the puzzle has 15,135,120,000 positions and 4! = 24 solutions, or you can consider colour permutations to be identical which means you have just one solution and 240·16! / 4!5 = 630,630,000 positions.
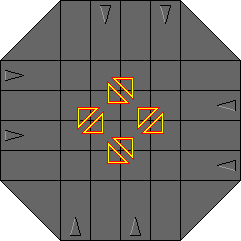
Suppose you slide a row, then a column, then slide the row back, and finally slide the column back. The effect of such a manoeuvre is that three tiles have been swapped around. The affected tiles are the one at the intersection of the column and row, and the adjacent tiles that are moved into that intersection. The picture on the right shows all possible 3-cycles that occur this way. To move the three tiles of a particular triangle in the picture, just alternately move the row and column that lie along the triangle sides.
With the above insight, it becomes quite easy to solve all the pieces of
the puzzle except for the corners. To move a corner, slide it in the direction
of the clockwise next corner (the only other direction to slide this tile brings
it outside the 4×4 area which is pointless). The tile can be moved using
the 3-cycle that doesn't involve the slide you just moved.
For example, the top-left corner can be moved to the right, and then with
the second row slide and second column slide you can do a 3-cycle. This way you
can replace the tile by one of the middle tiles of the second row. Then slide
the top row back to the left.
I won't describe a solution in full detail, but the steps below should suffice.