Jaap's Puzzle Page

The Super 3x3x1 / The Super Floppy

The Super 3x3x1 / The Super Floppy The Imitation Super Floppy

This puzzle is generally known as the Super Floppy, as it is a Floppy Cube which also allows quarter turns. This allows the corner pieces to move to locations above and below the edge pieces, changing the shape of the puzzle. It was also invented by Katsuhiko Okamoto.

There are two versions of the puzzle. The official version has an internal mechanism that blocks you from twisting a side consisting of only an edge piece without any corners. The imitation version lacks that mechanism, and by allowing you to twist an edge piece in isolation makes this easy puzzle much easier.

The number of positions:

There are 4 corners which can be in any of 12 locations. The edge pieces don't travel, but do have 4 orientations each. This gives a total of 12·11·10·9·44 = 3,041,280 positions. All of these are attainable.

Suppose we consider only the shape of the puzzle, ignore the colours. Then there are 12-choose-4 = 12!/(8!4!) = 495 ways the corners can be arranged if the puzzle has a fixed orientation. The puzzle as a whole has 8 orientations, so there are about 495/8 possible shapes. Some shapes have symmetry, so to calculate the exact number we need to apply Burnside's Lemma. This gives 72 distinct shapes. Only 18 shapes are mirror symmetric and the rest form 27 mirror image shape pairs.

I have used a computer search to find God's Algorithm, i.e. the shortest solution for each position. Every position of the official super floppy can be solved in at most 15 moves (9.8558 on average) or if a half turn is considered to be two moves it takes at most 17 moves (12.115 on average). The result for both metrics is shown in the following table:

Face turn metric
Q
u
a
r
t
e
r

t
u
r
n

m
e
t
r
i
c		 0123456789101112131415Total
011
188
244044
340128168
410240224474
51447367041,584
6249042,0162,1445,088
74243,1366,8804,56815,008
8532,71211,44017,74410,56042,509
998410,84836,56842,42420,960111,784
10646,16039,46094,38288,92032,896261,882
111,35223,840112,112199,504142,97636,864516,648
12316,22866,146222,228289,752158,29625,168767,849
1374417,736112,880254,816255,056102,62413,184757,040
1441,12020,05688,432160,112126,67235,0401,792433,228
15249927,44026,84851,24829,4082,432118,392
161201606722,4083,9361,7925769,565
1788
   Total   1   12   90   536   2,341   9,616   38,855   129,156   344,505   665,560   816,480   637,848   308,120   81,568   6,016   576   3,041,280

The eight QTM antipodes are positions with solved corners, three edges that need a half turn, and one that needs a quarter turn.

For the imitation super floppy need at most 13 moves to solve (9.0040 on average), or 16 (11.266 on average) if a half turn is considered to be two moves. The results are as follows:

Face turn metric
Q
u
a
r
t
e
r

t
u
r
n

m
e
t
r
i
c		 012345678910111213Total
011
188
244044
340160200
410256512778
51441,1521,3762,672
6241,1203,9204,0649,128
74645,48813,40810,28829,648
8533,59621,39440,09620,12885,267
91,09617,28072,84896,12031,168218,512
10607,41664,948195,408171,60032,720472,152
111,34431,416185,480357,784185,12017,792778,936
12296,33686,232325,300345,32880,2241,792845,241
1352818,272126,056241,45695,3603,360485,032
14498015,64054,65234,4642,19232107,964
1584082,5922,3682565,632
161481665
Total   1   12   90   584   3,301   15,536   64,935   226,464   602,629   1,027,956   861,916   230,224   7,600   32   3,041,280

If you ignore the colours and consider only the shape of the puzzle, then it takes at most 6 moves to solve. The results are as follows:

Face turn metric
Q
T
M		 0123456Total
011
144
21818
386472
46464128
5126496172
648016100
Total   1   4   26   140   132   176   16   495

Links to other useful pages:

Gentosha Toys is the manufacturer of this puzzle.

Solution:

Phase 1: Solve the shape, i.e. make it flat.

  1. Do any moves necessary to bring together an empty corner location and a corner piece that is sticking out.
  2. Hold the puzzle so that the front right corner location is empty, and the front edge has a corner piece sticking out above or below it.
  3. If the front left corner location is empty, then you can just turn the front to bring the corner that is sticking out into the main layer.
    If on the other hand the front left corner location is full, then turn the left side to make that corner location empty. Turn the front to insert the corner at the front right location. Finally turn the left side back to where it was.
  4. Repeat steps a-c until no more corners are sticking out.

The tree diagram below shows all possible shapes, and you can use it to solve the shapes optimally. The shapes coloured yellow are symmetric, the others occur in mirror image pairs, one on each side.

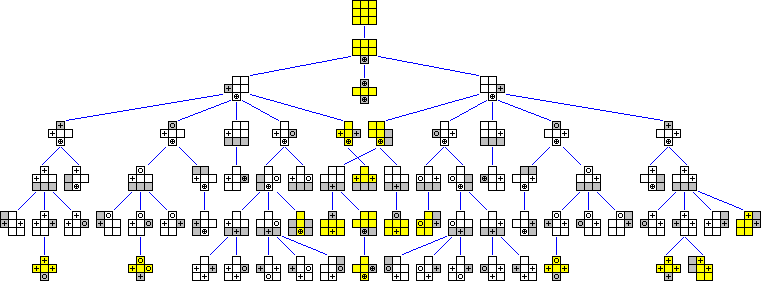
Tree diagram of floppy puzzle shapes

Phase 2: Solve the pieces.

  1. Solve the corners. Note that colour on the outside of an edge piece does not change when that side is rotated. Therefore the outside colour of the four edges can be used as reference points for placing the corner pieces. It is very easy to put one corner in place, then one of the adjacent corners without moving the first, and finally swapping the last two by a single move if necessary.
  2. If there is an edge piece that is not yet solved, then hold the puzzle so that the edge is at the front. Look at the side colours to see how much the edge needs to be twisted, and do one of the following:
    1. Quarter turn clockwise: R F R' F' L F L'
    2. Half turn: R F2 R' F2 R F R' F
    3. Quarter turn anti clockwise: R F' R' F L F' L'
    On the imitation super floppy there is a much easier way, namely to do R L so that the front edge piece is free, rotate the front edge piece to solve it, and then R' L' to restore the sides.
  3. Repeat step b until all the edges are solved.