Introduction

This page is the result of my ambitious attempt to list and classify all nice symmetric patterns of the Rubik's Cube. In doing this, the list of move sequences compiled by Mark Longridge has been an invaluable guide. I have limited myself to symmetric patterns, because these can be categorised more easily. Nevertheless it was a mammoth task, and I have undoubtedly made many mistakes. If you find an error, or have an improvement on the specific move sequences presented here, please let me know. Note that I often give more than one sequence for a pattern, either because one uses only half turns, or is easier to remember. If your browser supports it, you can click on a move sequence to open a new window showing the result of that sequence. Anyway, let's now get stuck in with a little bit of theory about symmetries of the cube.

If you want to colour the faces of a blank cube, and you have already decided which colours you want to be opposite each other, then there are 48 ways to do this: There are 6 possible colours for the U face (which determines the D face), 4 possibilities for the L/R faces, and then 2 possibilities left for F/B. Of these 48 possibilities 24 are the same except for a rotation, and the other 24 are their mirror images.

What the above paragraph illustrates is that the solved cube has a group of symmetry of size 48. For the moment lets just consider the group of 24 rotations only, and leave out the reflections. There are 3 types of axes for rotation:
Axis through a face centre, a 4-fold rotation (90, 180, 270 degrees)
Axis through a corner, a 3-fold rotation (120, 240 degrees)
Axis through an edge, a 2-fold rotation (180 degrees)
There are 3, 4, and 6 of these axes respectively, so there are 3*3+4*2+6*1=23 proper rotations. Of course there is also the identity, not rotating the cube at all, which accounts for all 24 rotations.

We know another group of size 24=4!, namely the group of permutations of 4 items, S₄, and it turns out that these two are essentially the same (i.e. isomorphic). The four items being permuted by the rotations of a cube are the cube's four main diagonals. After numbering the four main diagonals of the cube, any rotation can then be specified simply by using the standard cycle notation. If the main diagonals of the UFL, UBL, UBR, UFR corners are numbered 1-4 respectively, then (1234) is a clockwise quarter turn of the whole cube about the U face, (132) is a clockwise rotation about the UFR corner, and (24) is a rotation about the FR edge.

Lets now consider the reflections. The nicest reflection is the point reflection through the centre of the cube because this does not move the main diagonals at all. We can think any of the 24 reflected positions as a rotation of the cube combined with the point reflection. Let's denote that by underlining the permutation in cycle notation, e.g. (13)(24) is the reflection through the middle layer. The point reflection itself can be denoted by i, the reflection of the identity rotation i.

A mixed cube will usually no longer have the same symmetries as a solved cube, so when it is rotated or reflected it will look different. Nice patterns however will normally have some symmetry. Below I will try to examine each of the subgroups of the symmetry group of the cube, and look at what patterns have that kind of symmetry. Many of such patterns are not nice to look at because they have too many colours on the faces, but by restricting ourselves to patterns with at most 2 colours on each face, many beautiful patterns can be found.

Notation:

The standard notation is used mostly, i.e. the faces of the cube are denoted by the letters F, B, U, D, L, R. Clockwise turns simply use the relevant letter, half turns are denoted by the letter followed by a 2, and counter-clockwise quarter turns by the letter with an apostrophe. Four other types of move are used as well:

• Rs means the moves RL' (called a slice move)
• Ra means the moves RL (an anti-slice move)
• Rm means that the middle slice adjacent to the R face moves clockwise when looking from the R side.
• Rc means moving the whole cube a quarter turn clockwise when looking at the R face. Note that Rc = Rm Rs. This is not strictly speaking a real move.

Of course these moves can be done with respect to the other faces as well. Occasionally a move sequence has to be performed several times, and this is shown using an exponent, for example (U F2)²U would denote the sequence U F2 U F2 U.

For the symmetry groups I will use the cycle notation explained in the introduction but as it is not immediately clear what rotations/reflections such permutations represent, I will also use the following notation:

• m. A reflectional symmetry of any kind.
• r4. A 4-fold rotational symmetry (i.e. 90 degrees) around a face centre.
• r3. A 3-fold rotational symmetry (i.e. 120 degrees) around a corner.
• r2. A 2-fold rotational symmetry (i.e. 180 degrees) around a face or edge. (If the pattern has the 4-fold symmetry above, then this is assumed to be on a different axis, i.e. not r4 applied twice.)

Note that if a pattern has two r2 symmetries, or r4 and r2 symmetry, then there will automatically be a third r2, making a set of three orthogonal axes. To find the size of a symmetry group we must have a set of generators - a complete set of independent symmetries - and then multiply their orders. For example r4r2 has size 4*2=8 even though there is another r2 symmetry.

If you have a nice pattern and want to find out what its symmetry group is, simply see if it has any of the symmetries above. For example consider the 6-spot pattern, Rs Fs Us Rs = R L' F B' U D' R L'. All the pieces have been rotated about the main diagonal of the cube between URF and DLB. This pattern has symmetry m (through its centre point) and symmetry r3 (around the URF-DLB axis). It does not have any other symmetries. Therefore its symmetry group has size 2*3=6. The reflectional symmetry (m) may not be immediately obvious, but it can be demonstrated by applying the reflection to the move sequence. In other words, if we reflect each move (through the centre of the cube in this case) then R becomes L' and vice versa, F becomes B', etc. so the move sequence becomes L'RB'FD'UL'R which has the same effect. In fact, any sequence generated only by slice moves will have this m symmetry.

Since the whole group has size 48, there are 48/6=8 possible ways you could encounter a 6-spot patterned cube. What this suggests is that if someone does a 6-spot pattern on the cube and hands it to you behind your back, then you have only 1 in 8 chance of solving it without looking.

Often it will be necessary to specify what kind of symmetry we are using a little more precisely, and for this I will use the following:
m_f: A reflection through a plane parallel to a face of the cube.
m_c: A point reflection through the centre of the cube.
m_e: A reflection through a plane which goes through the centre and four corners of the cube. Note that this swaps two opposing edges.
r2_f: A 2-fold rotation around an axis through two opposite face centres.
r2_e: A 2-fold rotation around an axis through two opposite edge pieces.

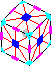
1. Symmetry mr4r3r2, <S₄, i>, 48.

The corners cannot be twisted, because if one were twisted then they all would have to be twisted in the same direction which is impossible. The edges can all be flipped. Any edge piece could be moved only if it swapped with the edge on the opposite side of the cube, and if so then all edges are swapped in that way. The corners cannot be swapped in that way since their orientations would then fix an orientation of the cube and restrict the symmetry. This leaves two main patterns:

1. The 6X pattern (a.k.a. Pons Asinorum) [p10, RCC 3.9.37]
   Rm2 Fm2 Um2 (6f*, 12q*)
   (Rs Fs)³
2. The superflip [p3,p179,p194,p195,p205]
   Ra D2 B' L2 F2 R2 Us' R' D2 Fa' D' F2 D' R2 U' F2 D' (20f*)
   R' U2 B L' F U' B D F Us L D2 F' R B' D F' U' B' Us (24q*)
   ((Rm U)⁴ Rc Uc')³

Note that both patterns have order 2, meaning that if they are performed twice then the cube is restored. Of course we also have:

3. 6X+Superflip (Applying both 1a and 1b) [p139]
   B' D' L' F' D' Fs' U Fs' R2 L Us F L U R D (19f*, 20q*)
4. The solved position! (Applying neither 1a nor 1b)

These 4 patterns form a group of order 4 (isomorphic to C₂², the direct product of two cyclic groups of order 2).

2. Symmetry r4r3r2, S₄, 24.

In section 1 we have already seen all positions with this symmetry that have reflectional symmetry as well. We now also want those that do not have reflectional symmetry. Because of r4 and r3, all faces would need 90 degree rotational symmetry, but the whole cube should not have any reflectional symmetry. This is impossible on a 3x3x3 cube, though it is possible on larger cubes because they have edge pieces that are not in the middle of the cube's edge, for example on a 4×4×4 cube you could cycle the three edges around each corner clockwise like this.

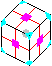
3. Symmetry m_fr3r2r2, <A₄, i>, 24.

It is fairly easy to show that if we combine r3 with a r2_e around an adjacent edge then we get an r4 rotation. We can therefore assume that the r2 symmetries are centred around faces.
We assume for the moment that we have reflectional symmetry through a slice (m_f). The central reflection m_c also lies in this group.

There is r3 symmetry about each corner, so the corner pieces cannot move unless they all swap with their opposites, and this is impossible because their orientation would then spoil the symmetry. Under the action of the r3r2r2 symmetries, they occur in two orbits; the URF, DLF, ULB, DRB corners form one tetrad, the other 4 the other tetrad. If one corner twists, then all other corners in the same orbit must twist in the same direction for the symmetry to hold. The reflection then shows that the two tetrads would have to twist in opposite directions. This gives the following pattern:

1. The supertwist [p82] {URF-,UFL+,ULB-,UBR+,DRB-,DFR+,DLF-,DBL+}
   B2 D2 B' R2 Ua L2 B' U2 F2 U' L2 Fa R2 U' (16f*)

This pattern obviously has order 3, because applying it three times returns the cube to the solved position. The patterns with this symmetry have 48/24=2 distinct orientations. Applying supertwist twice results in the same pattern in its other orientation.

Now consider the edges. These of course can be flipped as before, but again if one is flipped then they all must be (as they are in a single orbit). If an edge is moved to any position not in the same slice, then all the other edges are moved the same way and this spoils the reflectional symmetry. If an edge moves to the opposite position of the slice we just get 6X as before. However, if an edge moves to another position in the slice we get a beautiful pattern with six H faces.

2. The 6H pattern, type 1 [p175]
   U2 B2 R2 Us2 R2 F2 U2 (8f*)
   Ua' Ra' Fa2 Ua2 Ra' Ua
   (Ra Uc)³ Ra2 (Uc Ra)³

Combining this pattern with the 6H in the other orientation results in the Pons Asinorum 6X pattern (1a). The 3a and 3b patterns can also be combined in two ways.

3. 6H+supertwist, type 1
   F2 U2 B L2 Ua R2 B D2 F2 D' R2 Fa' R2 U' (16f*)
4. 6H+supertwist, type 2 (3c+1a)
   B L2 Ua L2 F U2 B2 U' L2 Fa' R2 U' F2 U2 (16f*)
5. Supertwist + 6X (3a+1a)
   R2 D' F2 Ra F2 U L2 D2 L F2 Ua F2 R' U2 (16f*)
6. Supertwist + superflip [p6] (3a+1b)
   R L U F D L U R' F' R F D U' F D' U' B F' L U (20f*,20q*)
7. Supertwist + superflip + 6X (3a+1a+1b) [p141]
   F R L2 U' R2 L' U' D2 R2 F D B D F2 U' R' D' F2 D2 L2 (20f*)
8. 6H pattern + superflip (3b+1b)
   U B' R' Fs U L Fs U' F' Us L2 R' F U' (17f*)
9. 6H+supertwist type 1 + superflip (3c+1b)
   U R B U L F U2 F2 D B2 U' R' B2 D2 R U B D' R2 U' (20f*)
10. 6H+supertwist type 2 + superflip (3d+1b)
    U' F2 D' L U F D2 L2 F' U' L2 D R2 U2 R B U L F U (20f*)

The patterns with this symmetry form a group of 24 elements (isomorphic to C₃×C₂³), of which 4 are 1a-d, the other 20 are the two orientations of the 10 patterns 3a-3j above.

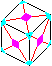
4. Symmetry m_er3r2r2, <(12)(34), (14)(23), (123), (24)>, 24.

This group restrict the movements of the pieces so much that only patterns with full cube symmetry mr4r3r2 remain. This is not the case on larger cubes however.

1. (UFl,DBl)(UbR,DbL)(dFR,dBL)(UBr,DFr)(UfL,DfR)(uFL,uBR)
   D2 (F2 R2)³ D2 L2 (u2 F2)² f2 u2 f2 L2 r2 u2 (f2 u2 r2)³ u2 r2

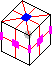
5. Symmetry mr4r2, <(1234), (24), i>, 16.

We can hold the cube so that the r4 symmetry is around the U-D axis. Lets consider the corners first. All the corners must be twisted the same amount with respect to the U/D layers, so they cannot be twisted at all. Suppose a corner is moved to a different position in the same U or D layer. Then all the other corners in the that layer must move in the same way, so they either move around in a 4-cycle, or opposite pairs are swapped. From R2 symmetry the other layer must then move the same way. The m symmetry then rules out a 4-cycle (whatever plane/point of reflection is used).

1. The 4+ pattern of order 2 [p16, RCC 3.9.6]
   R2 F2 R2 Us' F2 R2 F2 Us (10f*)
   Rs2 Fs2 U2 Rs2 Fs2 D2
   Fa Ua Ra2 Ua Fa Ua2
   (Fa2 Ua Ra2)²

If the corners swap U/D layers, then a similar argument shows there are only two possibilities; The corners swap with the corresponding one in the other layer, or they swap with the corner on the other side of cube.

2. 4-swap of corners type 1 (URF,DFR)(UFL,DLF)(ULB,DBL)(UBR,DRB)
   U' Fa U2 R2 U2 R2 Fa' R2 U2 R2 U' (13f*)
   U' Ra Fa Ra U D' Ra' Fa' Ra' D (16q*)
3. 4-swap of corners type 2 (URF,DBL)(UFL,DBR)(ULB,DRF)(UBR,DFL)
   U' F2 U2 F2 Ra F2 U2 F2 U2 Ra' U' (13f*)
   U Ra Fa Ra U' D Ra' Fa' Ra' D' (16q*)

Note that combining any two of these produces the third (and since they have order 2, they form a group with the identity). Now consider the edges. The middle layer edges form a separate orbit, so can be flipped separately from the other 8.

4. 4-flip of middle layer edges [p5]
   R Us2 L Us2 F2 Us L2 F' L2 Us' F2 R' (16f*)
5. 8-flip of U/D edges [p4] (5d+1b)
   (Ra Ua Fa)² (12f*,12q*)

The U/D edges have similar movements to the corners. An edge can swap with any of the other edges in the same slice, giving the following patterns.

6. The 2X pattern [p8, RCC 3.9.39] (UF,DF)(UR,DR)(UB,DB)(UL,DL)
   F2 R2 Fs2 R2 F2 Rs2 (8f*)
   Ua Fs2 Us' Fs2 U2
   (R2 Uc)¹²
7. The vertical 4H pattern of order 2, type 1 [p160, RCC 3.9.7] (UR,UL)(DR,DL)(UF,UB)(DF,DB)
   (U2 Fs2 Rs2)² (10f*)
   Ra Ua Fa2 Ua Ra (12q*)
8. The 2X + vertical 4H of order 2, type 1[p72] (UF,DB)(UB,DF)(UL,DR)(UR,DL)
   (Us Rs2)² (8f*,12q*)
   L2 Us2 L2 F2 Us2 F2 Us2

Again, any two of these combine to make the third.

The middle layer edges must remain in the layer. A 4-cycle is not possible because it is an odd permutation (and there is no other odd permutation available to combine it with), and the edges can therefore only move to their opposite positions.

9. The horizontal 4H pattern of order 2. [p26, RCC 3.9.3] (FR,BL)(FL,BR)
   Us Rs2 Us' Fs2 (8f*)
   Rs Us Rs' Us Rs Us' (12q*)
   R2 (Um2 F2)² R2

Note that 5h+5i=1a, the Pons Asinorum.

The patterns above generate the group of all 128 patterns with this symmetry (the group is isomorphic to C₂⁷), including the subgroup with full cube symmetry we have already seen. Thus there are 124 patterns which have exactly this symmetry.

The patterns 5b-e place more than two colours on each face. The remaining patterns generate a group of 16 nice patterns (including the identity and the patterns 5a, 5f-i, 1a). All these patterns can be generated by using only half turns of the faces, though it is sometimes quicker to use quarter turns as well. Here are sequences for all of them.

10. Vertical 4I pattern [p23, RCC 3.9.13] (5a+5i)
    (F2 R2 B2)² (6f*,12q*)
11. 2X + 4+ [p27] (5a+5f)
    Rs2 Us' Rs2 Us (8f*)
    Rs Fs' Rs' Fs Rs Fs' (12q*)
    F2 Us2 F2 R2 Us2 R2
12. 2X + horizontal 4H (5i+5f)
    U2 Fs2 Rs2 D2 (6f*,12q*)
    Ua Fa2 Ra2 Ua (12q*)
13. 2X + vertical 4I (5a+5i+5f)
    Rs2 Fs2 (4f*,8q*)
14. Horizontal 4I (5a+5g)
    Us2 (2f*,4q*)
15. 4X pattern [p9, RCC 3.9.14] (5i+5g)
    R2 F2 Rs2 F2 L2 Us2 (8f*)
16. 4O or 4-spot pattern [p13, RCC 3.9.5] (5a+5i+5g)
    Rm2 Um Rm2 Um' (8f*,12q*)
    R2 (Um2 F2)² R2 Um2
17. 2X + horizontal 4I (5a+5h)
    U2 Rs2 Us' Rs2 Us U2 (9f*)
    L2 F2 Rs2 F2 L2 Fs2 Us2
18. 2X + 4O [p12] (5a+5i+5h)
    U2 Fs2 Rs2 U2 (6f*,12q*)
    Ua Ra2 Fa2 Ua' (12q*)

6. Symmetry r3r2r2, A₄, 12.

This is tetrahedral symmetry without reflection. There is r3 symmetry about each corner, so the corner pieces cannot move unless they all swap with their opposites, and this is impossible because their orientation would spoil the symmetry. The corners can only twist by 3a. The edges lie in a single orbit, so if one flips or moves, then they are all flipped/moved in the same way. They can be flipped by 1b, and moved not only by 1a/3b but also in four 3-cycles as follows:

1. Four 3-cycles of edges, type 1
   D' Fa' D' Ra D' Fs2 Rs2 U' Fa U' Ra' U' (18f*)
2. Four 3-cycles of edges, type 2 (6a+1a)
   R2 F Rs' Fa D' Ra' D' F2 L Ua' L' F2 U' (17f*)

These two sequences come in 4 forms each (rotation and/or mirror image) so with 1a, 3b, 3b' and the identity, all 12 possible edge movements are accounted for. This group therefore contains 72 patterns. There are few nice patterns in this group because they all have at least 3 colours on each face, but the following are not too bad:

3. Pinwheels [p143] (6a+3a')
   Fa Ra Fa' Ua' Ra Ua (12f*,12q*)
4. Pinwheels + 6X [p201] (6b+3a)
   Fa Ra' Fa Ua' Ra Ua' (12f*,12q*)

7. Symmetry mr3r2, <(123), (12), i>, 12.

There is only one axis with r3 symmetry, because otherwise the pattern will have tetrahedral symmetry which was discussed above. The axis of rotation of the r2 symmetry must therefore be perpendicular to the r3 axis (i.e. through an edge, r2_e). The m symmetry can be any reflection that keeps the r3 axis in place (so is either m_c through the centre, or m_e through a plane containing the r3 axis).

Lets consider the corner pieces first. The corners on the r3 axis cannot move at all, because if they left the r3 axis then the r3 symmetry would be spoiled, and if they swapped then their orientations would spoil the r3 symmetry also. The other 6 corners form one orbit, so the movement of one determines the others. Each corner lies in a plane of reflection m_e, so cannot be twisted, and could only possibly move if it swapped with the opposite corner (which lies in the same plane). Therefore the only way to move the corners would be a triple swap, but this is an odd permutation and therefore cannot occur without edges being moved as well.

The six edges adjacent to the corners on the r3 axis can only be moved if they swap with their opposites (because the planes of reflectional m symmetry go through only those pairs of edges). This is an odd permutation, so it cannot be done without moving the corners as mentioned above.

1. Triple edge swap, triple corner swap type 1 (LUF,RBD)(ULB,DFR)(BRU,FDL)(UF,DB)(UR,DL)(LB,RF)
   U L Ua L' Ua' R B2 U2 B2 Ra' U' (14f*,17q*)

The same six edges can also be flipped.

2. Six edge flip type 1, {UF+,DB+,UR+,DL+,LB+,RF+}
   D F R' U2 B2 U2 R' U' Rs' B U' R2 F2 R2 U' R' U' (18f*)
3. Triple edge swap, triple corner swap type 2 (7a+7b) (LUF,RBD)(ULB,DFR)(BRU,FDL)(UF,BD)(UR,LD)(LB,FR)
   U L U B' U' L R2 U2 B U' L' U' B F2 R2 B' F2 U' (18f*)

This is one of the nicer patterns in this group.

The other six edges can also move. They can be swapped with their opposites, but again cannot move in any other way. Patterns using this can be considered to be patterns where these edges do not move followed by the Pons Asinorum (1a). These edges can also be flipped, which is like following one of the previous patterns by the superflip (1b).

There are 16 patterns in this symmetry group (it is isomorphic to C₂⁴). Excluding the 4 patterns with full cube symmetry, leaves 7a-c, and the 12 patterns listed below.

4. Triple edge swap, triple corner swap, type 3. (7a+1a)
   L2 B' U B' D' Fa D2 F' U' B L2 U' F2 U2 R2 U' (17f*)
5. Six edge flip + Pons Asinorum. (7b+1a)
   R' B' U' B2 R' B' D' U L U B2 F D2 U' L U F R' U' (19f*)
6. Triple edge swap, triple corner swap, type 4. (7c+1a)
   L R2 D' B F2 L2 R' B' D2 R2 Ua' R' D2 B Us' F' U' (19f*)
7. Triple edge swap, triple corner swap, six edge flip, type 1. (7a+1b)
   F' D' R U2 Fa L2 B2 R2 D2 L Us R2 U2 R B' U' (18f*)
8. Six edge flip, type 2. (7b+1b)
   U2 Rs2 F' R' U B R' D Fs2 L' B' D R B' U' (17f*)
9. Triple edge swap, triple corner swap, six edge flip, type 2. (7c+1b)
   F L' Fs2 U B2 F' D R D2 B2 U F2 L Fa D' R' U' (19f*)
10. Triple edge swap, triple corner swap, six edge flip, type 3. (7a+1a+1b)
    D' U2 B2 Rs2 B' R Ds Ls D Fa2 R Fa' R U' (19f*)
11. Six edge flip type 2 + Pons Asinorum. (7b+1a+1b)
    D B D' L U B F' R' F' L B L R' D' F' U R' U' (18f*)
12. Triple edge swap, triple corner swap, six edge flip, type 4. (7c+1a+1b)
    D2 B' U2 L B2 D2 U F2 D B2 R' B2 U B D' F2 U' (17f*)