



The Varikon Box 3×3×3 puzzle superficially looks like a normal 3×3×3 sliding cube puzzle, similar to Peter's Black Hole, IQube, and Magic Jack. It has a transparent box, apparently containing 26 cubes and a space, so that the cubes can slide around. It differs however in that the cubes at the face centres are fixed onto the central cube, so that there are only 19 moving cubes, arranged along the corners and edges of the box. The box also doesn't have (nor need to have) holes for you to slide the cubes, as simply tilting the box suffices. The cubes are red, and each side has a white or blue spot. When solved, all the blue spots are on the outside, with only the space showing three white spots.
There is a tiny hole near one corner of the box, into which you can insert a small rubber pin. This prevents the puzzle from getting mixed up accidentally.
Inversion is an equivalent puzzle which does not have a transparent box. Instead the face centres have rims that keep the cubes contained. Its colour scheme is also different - every small cube looks the same, with three red faces around one corner and three blue faces around another. This means that there are many identical pieces, and also that the puzzle can be made all red or all blue, including the parts visible at the space.
The Varikon Box was invented by Csaba Postasy, Gabor Eszes, and Miklos Zagoni. The German
version of its patent, DE 3,027,556, was
published on 19 June 1981.
Inversion was invented by Patrick A. Roberts. Its patent, US 4,511,144, was published on 16 April 1985.
If your browser supports it, you can click on the link below to play with a Javascript version of the Varikon 3×3×3.
There are 19 loose cubes and a space. Any even cube permutation is possible,
but no odd permutations, so for any position of the space there are 19!/2
cube positions. The space can only really be in the corners, giving a total
of 8·19!/2 = 486,580,401,635,328,000 positions.
The Inversion has many identical pieces. The pieces only differ in their
orientation, and there are 8 orientations they can have. The 19 pieces split
into sets of 3, 3, 3, 3, 2, 2, 2, 1 identically oriented pieces. These can be
invisibly rearranged in 2!33!4 /2 ways by even permutations.
The actual number of positions is therefore 8·19! / 2!33!4
= 93,861,960,192,000.
I will use the Rubik's cube notation, so each letter F, L, U, B, R, D denote a clockwise shifts of all the cube around the Front, Left, Up, Back, Right, Down face respectively. Similarly, I will denote each little cube location by three letters (for a corner location) or two letters (for an edge location), namely the letters of the outside faces of that cube location.
The pieces of the Varikon Box are unique, so you can determine where each piece belongs. A piece belongs in such a spot that all its blue faces are visible, and all its red faces are hidden. To solve the puzzle you therefore merely have to know how to move the pieces to where you want them.
Phase 1: Solve everything but the U layer.
Phase 2: Solve the top layer.
Every piece on the Inversion puzzle has 3 faces of each colour. There is clearly only
one corner of the puzzle where that piece could belong, and if there are several identical
pieces then they go in that corner and in one or more of the adjacent spots. An edge location
therefore has two types of piece that could fit, namely the type that would fit either of
the adjacent corners. There is however one corner for which there is only piece available, so
each edge location next to it has only one type of piece that could fit.
When it is solved, the three pieces next to the gap must be identical, so at the end the gap
must lie at one of the corners for which there are 3 pieces available.
The picture below shows a blue and a red solution.
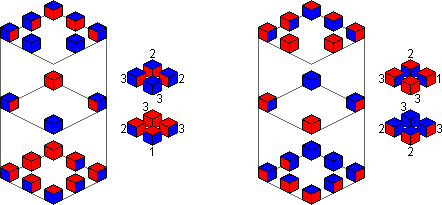
The Inversion puzzle can be solved using the Varikon solution above. It is generally a little easier though to solve all the bottom corners before the middle layer. Once the bottom layer is solved, any pieces with a wrong colour on top will have to be put in the middle layer.