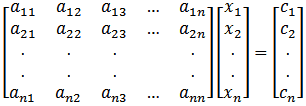
Your Psion Organiser II and the plug-in Maths pack form a sophisticated pocket computer system. While they have been designed for ease of use, we suggest that you read this booklet in conjunction with your Organiser II Operating Manual, to ensure that you make the best of their capabilities.
To avoid possible damage to your Organiser II and all associated Psion products, they should not be subjected to extremes of temperature or humidity, nor should they be subjected to hard knocks or immersed in liquids. Do not use volatile fluids when cleaning the case.
If within 12 months of purchase, this Program Pack can be shown to be faulty, Psion will (at the option of the purchaser) refund the purchase price or replace the Program Pack. All other liability arising from any error, defect or failure of the Program Pack is excluded, including incidental or consequential damage or loss. This does not affect your statutory consumer rights.
COPYRIGHT PSION LIMITED 1986
DESIGN REGISTRATION APPLICATIONS
NOS 1019736 AND 1019737
PATENT APPLICATION NO. 8412628
INTRODUCTION 1 INSTALLING THE MATHS PACK 2 SOLVING EQUATIONS Solving Quadratic, Cubic, and Generalised equations in one variable. Solving sets of linear equations in up to 10 variables. Finding Eigenvalues, and evaluating determinants. 3 INTEGRATING A FUNCTION Numerical integration of analytical or numeric functions 4 STATISTICS Calculating Chi squared, Confidence Levels. Calculating Correlation Coefficients. Calculating the Error Function. 5 CURVE FITTING Fitting polynomials to experimental data. 6 FUNCTIONS Evaluating Bessel Functions of the first kind, the Gamma Function, factorials, inverse trigonometric functions, hyperbolic trigonometric functions. 7 TROUBLESHOOTING 8 WARRANTY
Typeset by Keywords, Manchester
Printed by Premier Metropolis Limited, London
In the box containing this manual you will have found a program pack labelled MATHS PACK for your Organiser II. This pack is identical to an ordinary Datapak, except that it comes pre-filled with programs and useful functions. It is plugged into your Organiser II in exactly the same way as an ordinary Datapak, remove the drive cover (or Datapak if fitted) from one of the drives of your Organiser by pulling on the knurled surface, and simply insert the Maths Pack in the empty slot in the normal way.
The Maths Pack is a substantial software system which enhances the Organiser II, turning it into a powerful tool for mathematical analysis. It consists of a collection of procedures written specially for the Organiser II in OPL. These procedures are saved on the Maths Pack in translated form. They provide a wide range of calculations within a number of specialised areas, and have been written to be easy to use and extremely fast.
As in the CALC mode of Organiser II, all calculations are performed internally to an accuracy of 12 digits, although the Maths Pack usually displays results to fewer digits in order to make the output easier to read.
The procedures and functions in the Maths Pack have been designed for maximum flexibility of use, so that you can incorporate them into your own OPL prograrns. Alternatively you might wish to customise your Organiser II by having specific procedures directly available from the top level menu.
You may install the Maths Pack so that its facilities are available from its own MATHS menu, or you may call the various procedures directly from the CALC or RUN functions.
Remove the Datapak or device cover from one of the slots on the back of the machine and fit the Maths pack firmly in place, then select the DIR option from the top level menu of the Organiser. This will display the name of the first procedure in the pack, and successive presses of the EXE key will display names of the rest. You will see that the Maths Pack consists of a large set of procedures and functions. These can be executed directly in CALC mode simply by typing the function name with its arguments (if any) in brackets, for example:
2.5*asin:(0.3331)/1.2323
or
sqr(jbess:(3,6))
Note the ":" in the procedure names.
These procedures can also be evaluated directly in RUN mode, by typing in the procedure name followed by the values of its arguments (if any), and then pressing the EXE key. Should the procedure require further input, you will be prompted for this when necessary.
To access the Maths pack routines from the top level menu, you may either
or
See Chapter 16 of the basic Organiser manual for details on customising the main menu in this way. However, bear in mind that in this case you cannot pass arguments to function procedures from the main menu.
Should you wish to follow this route for a function procedure (e.g. sinh:(x)) you should create and translate a shell procedure which prompts for the arguments and passes these as parameters to the required procedure, and install the name of this shell procedure at the top level menu.
xsinh: LOCAL x CLS :PRINT"Enter x" :AT 1,2 INPUT X RETURN sinh:(x)
If you translate and save this procedure and install the name xsinh at the top level, you will be prompted for the parameters needed by the routine sinh:(x).
If you have installed MATHS in your top-level menu, when you select this option, you are immediately provided with the Maths Menu, which groups together the various procedures and functions according to the types of calculation they perform. The categories are
| SOLVE | for solving equations |
|---|---|
| INTEGRATE | for performing numerical integration |
| STATISTICS | for analysing statistical data |
| CURVE | for fitting polynomials to observed data |
| FUNCTIONS | for evaluating special functions |
| QUIT | exits the Maths Pack and returns to top level |
The FUNCTIONS are all procedures which have been defined with arguments in the form procname:(arg1,arg2,...) and may therefore also be called directly from any of your own programs.
On selecting an option from the Maths menu a series of sub-menus will be encountered giving you the various options available to you at each point, including QUIT which enables you to return to the Organiser's main menu.
Select SOLVE from the Maths menu and you will be presented with a submenu containing the following options
QUAD / CUBIC / DET / NEWTON / MATSOL / EIGEN / QUIT
Select the QUIT option to return to the Maths menu, from which you may select another task, or quit.
This program solves the quadratic equation
ax2 + bx + c = 0
and returns both real and imaginary roots (if any). Simply run the procedure and enter values for a, b and c when prompted. Long results which scroll across the screen can be stopped and examined using the LEFT and RIGHT cursor keys. As each root is displayed, the program waits for you to press any key before displaying the next result, to give you an opportunity to note the values.
This program solves the equation
ax3 + bx2 + cx + d = 0
and produces the real and imaginary roots.
On selecting CUBIC you are presented with a menu containing the following options
INPUT / EDIT / SOLVE / QUIT
Selecting the INPUT option from the menu enables you to enter the coefficients a, b, c and d. The EDIT option allows you to examine and alter the coefficients, while SOLVE performs the calculation and displays the results. Once again, long results which scroll across the screen can be stopped and examined using the LEFT and RIGHT cursor keys. As each root is displayed, the program waits for you to press any key before displaying the next result, to give you an opportunity to note the values.
To quit the program and return to the main menu, select the QUIT option.
Given any well-behaved analytical function f(x), NEWTON solves the equation
f(x)=0
using the Newton-Raphson method.
Prior to using NEWTON the function f(x) must be defined in a procedure called func:(x) and this should be saved in its translated form.
e.g. to solve
sin(2x) - tan(x) = 0
you must translate and save the following:
func:(alpha) return sin(2*alpha)-tan(alpha)
The Maths pack already has saved within it, by way of illustration, a procedure called func:(x) which evaluates the expression x.sin(x)-x. Should you wish to define another function for use with NEWTON, delete the existing procedure func: and replace it with the new one.
NEWTON asks you to input an approximate solution as a starting point, and computes the nearest solution, to an accuracy of better than 1 part in a million. While looking for the root, it displays the number of iterations performed.
You should bear in mind the fact that if f(x)=0 has more than one- root, the solution found will depend upon the initial starting value of x you give and how the: gradient of the function behaves.
If you think the calculation has gone into a loop, its execution can be terminated by pressing the ON/CLEAR key and then the Q key.
This procedure solves the set of linear equations
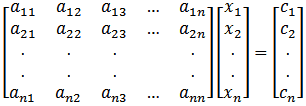
for up to ten variables. Given the elements of the coefficient matrix "a", and those of the right-hand "c" vector, MATSOL solves for the variables x1, x2, ..., xn in turn. The method used is gaussian elimination.
The program is menu driven, the options being
INPUT / EDIT / CALC / QUIT
Selecting the INPUT option, you are prompted to enter the dimension of the coefficient matrix (i.e. the number of variables) and then the elements of the coefficient matrix with its corresponding element of the "c" vector, row by row.
When all of the data has been entered, you are returned to the sub-menu from where you may review and change any at the coefficients by choosing the EDIT option You are first asked to specify which element to edit, and its current value is displayed together with the question "Correct (y/n)?". If you answer "n" you will be prompted to enter the correct value, after which you will be asked whether or not to edit another value. Replying "n" at this stage finishes the editing and mining you to the sub-menu.
The CALC option calculates the solution of the set of equations by gaussian elimination and displays the value of the first variable. The Organiser will wait until you press any key before going on to display the next variable's value.
After displaying the solutions, MATSOL then displays the value of the determinant of a, before returning you to the menu once again, at which point you may edit the coefficients and recalculate, or QUIT.
This procedure finds the real and complex eigenvalues of a three by three matrix of real numbers, given the elements of that matrix.
The Eigenvalues are the values at λ (lambda) which satisfy the characteristic equation:
|A - λI| = 0
where A is the square matrix in question, and I is the Unit Matrix.
On selecting EIGEN you are presented with the sub-menu
INPUT / EDIT / CALC / QUIT
The INPUT option prompts for the elements of matrix A. The EDIT option enables you to review and alter the data entered, after which you are one again returned to the sub-menu. The CALC option computers the Eigenvalues, and this option may be entered repeatedly, thus enabling you to observe changes in the matrix elements.
The results are displayed one by one. If a result is too long to fit on a single line, it will automatically scroll. Use of the LEFT and RIGHT cursor keys stops the scrolling. Pressing any other key causes the next result to be displayed.
This procedure computes the determinant of the matrix
|aij|
where aij is any square matrix of dimension up to 10 × 10
You should note that this program uses gaussian elimination which involves multiplications and divisions, and this leads to the possibility of small rounding errors being found where integer results might have been expected.
DET is menu driven:
INPUT / EDIT / CALC / QUIT
The INPUT option prompts for the elements of the matrix row by row. The EDIT option enables these values to be reviewed and altered, while the CALC option evaluates the determinant. For a large determinant, this could take a few seconds. The QUIT option returns you to the main menu.
There is only one procedure in the Maths pack under the topic Integration to perform numerical integration. This is a generalised procedure and can be used to integrate any analytical or numeric function.
This program performs the numerical integration of a given function using Simpson's Rule
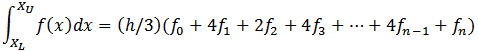
where (n + 1) evenly spaced samples of the function f(x) are taken in the interval xL to xU, and h = (xU - xL)/n.
INTEGR can handle integrands either in analytical or numerical form. If an analytical integrand is supplied, the program automatically performs the sampling and applies the above formula.
If the integrand is analytical, it must be supplied to the program in the form of a translated function procedure previously saved under the name func:(x).
For example, to perform
you must first enter and translate the following:
func:(x) return x*sin(x)
By way of illustration, the Maths pack is supplied with a translated function func:(x) which returns the value of x.sin(x)-x. Delete this and create your own procedure called func:(x) if you require to integrate an analytical function.
The program is menu driven, its sub-menu being:
INPUT / EDIT / CALC / QUIT
If you select INPUT you are prompted to specify whether a numeric or analytic integrand will be supplied. You are then asked to specify the range over which to integrate, and how many evenly spaced points (including the endpoints) to use. The maximum number of points is 99. Calculation of the sample values is performed at this point, resulting in a short delay before proceding.
If a numeric integrand is to be used, the program prompts for the number of sample values to be entered, and then the values at the appropriate points. When data entry is complete, you are returned automatically to the sub-menu.
If you now select EDIT, you will be able to examine and alter the data you have input. You will be shown the current value of each point. If you want to keep it, simply press EXE to go on to the next one. Otherwise alter the value and press EXE.
To perform the integration, select the CALC option from the sub-menu. The QUIT option exits the program.
This set of procedures provides you with a powerful tool for the statistical analysis of data. On selecting the STATISTICS option in the Maths menu, you will be provided with the Statistics sub- menu, containing the following items:
CHI / CONF / CORREL / ERF /QUIT
If you select the QUIT option, you will return to the Main menu of the Maths pack
Selecting any of the remaining options performs the specific tasks within each procedure as described below,
This procedure calculates chi-squared. It prompts directly for the confidence level and the number of degrees of freedom. The confidence level must lie between 0 and 1, and up to 100 degrees of freedom will be accepted.
This function returns the Confidence Level, given chi-squared and the number of degrees of freedom.
If CONF is called from the Statistics sub-menu, you will be prompted to enter the value of chi- squared and the number of degrees of freedom, after which it calculates the confidence level, and holds the display until you press any key.
If you are using CONF directly from within your program, it must be passed two parameters. The first is the value of Chi-squared, and the second is the number of degrees of freedom. Given these values, conf:() returns the associated level of confidence as a decimal value less than 1. The number of degrees of freedom must be less than 100. CONF is called by
z=conf:(chs,degs)
This function returns the value of the normal distribution function:
by using Hasting's approximation. The maximum error is less than 3 parts in ten million.
If the function is called by selecting the ERF option from the Statistics sub-menu, you will be prompted to enter the value of t. The result will then be displayed and held until any key is pressed.
Alternatively, ERF may be called either directly or from within one of your programs, in which case it must be called with one parameter. ERF is called by z = erf:(t)
This program enables you to enter observations on up to five different variables, and to calculate the correlation coefficients between pairs of variables, defined by:
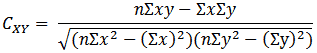
where x and y are the observed values of one pair of simultaneously observed variables, and n is the number of such observations made.
Obviously, if there are five variables being observed, there will be ten such correlation coefficients, ignoring correlations of each variable with itself.
The program will handle a total of up to 500 (200 on Model CM) observations spread over however many variables are being recorded. Thus, if you are observing 5 variables, you can enter up to 100 observations. If you are observing 2 variables, you can enter up to 250 observations.
On first starting up, the program checks to see that sufficient memory is available on device A: and if not, it invites you to make the space available and returns you to the top level.
Assuming sufficient space is available, the program presents a sub-menu of options
INPUT / FILE-IN / CALC / FILE-OUT / QUIT
The INPUT option allows you to enter data via the keyboard. It asks you to enter the names af the variables you are observing, and how many observations have been made, and then prompts for each variable in turn. When all observations have been entered, you are returned to the sub- menu again.
The FILE-IN option allows you to enter data from a previously saved file, rather than key it in manually. This data needs to have been previously saved to the file either by CORREL or it might have been created independently. In the latter case, the structure of the file need be very simple, each record consisting merely of a fixed number of numeric fields, entered in the same order as the variables. The number of fields (variables) can be 2,3,4 or 5. On invoking FILE-IN you are first asked for the name of the file, and then you are then prompted to enter how many variables were observed and then names (in order). The program will then read in the data and return you to the sub-menu when complete.
Note that an error condition will result if the number of variables contained in the file you are trying to read does not agree with the number of variables you specify.
After keying in all of your data via the keyboard, you might want to save it on a Datapak for future reference. The FILE-OUT option permits you to do this. This option can be invoked at any stage after completion of data entry.
The CALC option of the sub-menu performs the computation of the correlation coefficients, and permits you to select the pairs of variables you are correlating. The variable names are displayed in a menu. Selecting one causes the names to be displayed again. On selecting the second, the correlation coefficient between those two variables is displayed. The result will be held until you press any key, alter which you will be returned to the variable name menu. Choosing the END option here returns you to CORREL's functional sub-menu.
There is a single procedure in this topic selected by choosing the CURVE option of the Maths Menu.
This program allows you to enter up to 100 pairs of observed values (x, y), and to find the polynomial:
y = an xn + an-1 xn-1 + ... + a0
which gives the best fit through these points. Polynomials up to order 9 can be used, and the method used is that of minimizing the sum of the squares of the deviations of the observed points from the ideal curve.
On entering the procedure, you are given a sub-menu:
INPUT / EDIT / DEGREE / CALC / QUIT
On selecting the INPUT option, you are prompted for the number of points to be entered, and then for all of the x— and y-values. When all of the data has been entered, you are returned to the menu.
The EDIT option allows you to edit your data. If the data is correct, press EXE, or change to the desired value and press EXE.
Selecting the DEGREE option enables you to enter the degree of the polynomial required to fit, and the CALC option performs the computation.
The results are the coefficients of each power of x displayed consecutively. Press any key to display the next result.
Finally, when all the relevant coefficients have been displayed, the procedure calculates the Root Mean Square Deviation of your data from the fitted curve, as an indication of the quality of the fit.
After determining the polynomial, CURVE will ask if you want to evaluate points on the interpolated curve. If you answer "y" you will then be prompted for an x-value, and the corresponding y-value will be displayed.
The same set of data can be re-used to test for a fit to other polynomials within the range. Simply go to the top sub menu, change the DEGREE and execute CALC again.
The FUNCTION option of the Maths menu allows you to evaluate a range of functions, and be prompted by the Organiser for the required arguments. This contrasts with the way these functions are used in direct mode, where their arguments must be supplied as parameters at the time of calling.
On selecting the FUNCTIONS option of the Maths Menu, a sub-menu containing the following options is displayed:
GAM / JBESS / FAC / ACOS / ASIN / SINH / COSH / TANH / QUIT
Selecting QUIT exits FUNCTION and returns you to the Maths main menu.
Selecting any of the other options will perform the evaluations as described in the following sections:
This function returns the value of the Gamma Function:
Γ(n)
where Γ(n+1) = n Γ(n)
and Γ(1/2) = √π
for integer or half-integer arguments.
GAM must be called with one parameter. If the parameter supplied is non-integer, the function automatically rounds to the nearest half-integer. Negative values are outside the range of the calculation. GAM is called by
z = gam:(n)
This function returns the value of the Bessel function:
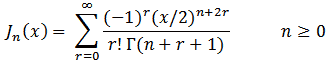
and must be called with two parameters. The first is n, the order of the function, and must be a positive integer or half-integer less than 10. The second is x, the argument.
As in gam:(), if n is non-integer it will be rounded to the nearest half-integer. JBESS is called by
z = jbess:(n,x)
This function returns the (real) factorial of the (integer) parameter provided.
n! = n(n—1)(n-2)....3.2.l
and is called by
z=fac:(i%}
Given an argument in the range -1 to +1, ACOS returns the angle in radians. ACOS is called by
y = acos:(x)
Given an argument in the range —1 to +1, ASIN returns the angle in radians. ASIN is called by
y = asin:(x)
Given an argument, SINH returns
(exp(x)-exp(-x))/2
SINH is called by
y = sinh:(x)
Given an argument, COSH returns
(exp(x)+exp(-x))/2
COSH is called by
y = cosh:(x)
Given an argument x, TANH returns
1-2/(exp(2x)+1)
TANH is called by
y = tanh:(x)
If nothing appears to be happening when you expect otherwise, this could be because:
Your PSION Organiser II Program Pack carries a one year warranty against mechanical or electrical failure other than in the case of misuse or damage arising from negligence. There are no user- servicable parts within your program pack, and any attempt to dismantle or repair your program pack other than by an Appointed Psion Service Agent will invalidate this warranty.
Should you experience any problems consult both this and your basic Organiser II Operating Manual with particular reference to the troubleshooting section. If you find no solution to your problem, send your program pack in suitably protective packaging to:
Service Department
Psion Limited
Psion House
18 Harcourt Street
London W1H 1DT
Psion can accept no responsibility for goods damaged in transit to us. This warranty does not affect your statutory rights.