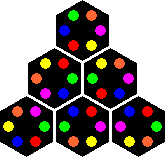
Drive Ya Nuts is a puzzle consisting of seven large hexagonal nuts, each of which has its six edges marked by the numbers 1 to 6 in some order. The aim is to put them in a hexagonal arrangement (one in the centre, the other six touching each side) so that every pair of touching sides have matching numbers. It was manufactured in plastic by Milton Bradley around 1987.







The numbers in clockwise order on each nut are 123456, 143652, 146235, 162453, 164253, 165324, and 165432.
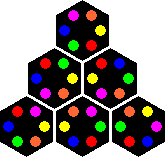
Circus Seven ('The Mind Exerciser') is a different version of exactly the same puzzle. It has seven hexagonal pieces, shaped a bit like circus tents, which have coloured stickers on the sides. Each piece has six colours, and there is a perfect correspondence with the numbers of the Drive Ya Nuts puzzle. The numbers 1 to 6 correspond to the colours red, green, blue, yellow, white, and orange respectively. It was manufactured by the Masudaya Corporation of Japan.

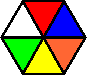
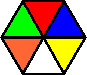


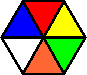
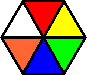
Circus Puzzler is one of many colour variations of the Circus Seven puzzle. It looks like the same puzzle except that the colours are arranged differently, and it has no markings on the plastic box. There are three pairs of identical pieces. Note also that all the pieces have white opposite yellow, green opposite blue, and red opposite orange.




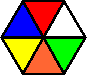


Below I list several other colour variations. Whereas the Circus Seven puzzle has a leaflet that explains the puzzle in remarkably well-written English, the Circus Puzzler's leaflet is badly written. I reproduce it verbatim below.
Test your intellingence.
Can you make all the contacted edges of chesses for the same colour shortly?
(1) Take out seven chesses and separate them to match on the edges of chesses with six different colours as red, white, orange, blue, green and yellow.
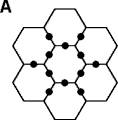
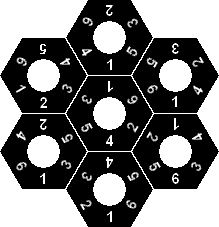
(2) Pick any one of them and put it on the center. The other six chesses will be arranged as shown in Figure (A) below.
(3) If you can make all the contacted edges for the same colour as shown in figure (B) below, then you will find the correct solution.
 |
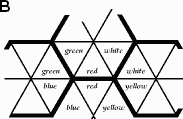 |
Indicates the contacted portions of the 12 edges.
There are several other colour variations of this puzzle, sometimes also sold under the same names or as Color Matcher. It is not clear how many variations there are, but here I list the ones I have seen pictures of. These variations are all different, even if the colours are swapped.
Variation A:


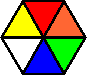
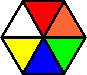
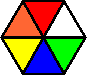

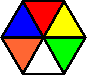
Note that all but one of the pieces have red opposite blue.
Variation B:

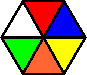





Note that the last two pieces are identical.
Variation C:
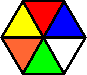
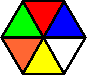


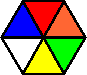
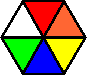
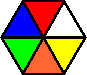
Variation D:
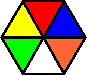
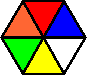

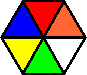


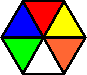
Variation E:
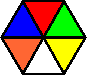




This version is smaller, about 2/3 the size of the standard versions.
Variation F:







This version is made of wood, and is called the Spot Colour Puzzle.
If your browser supports JavaScript, then you can play some of these Circus Puzzle variations by clicking the link below. You can even change the colour scheme to match any other colour variation you might have, and then let the computer find all the solutions.
Thinkominos is another matching puzzle with hexagonal pieces, made by Pressman in 1984. This time there are six pieces, also with six colours each. The aim is to create a triangle.

There are 7 pieces with 6 orientations. This gives 7!·67
ways. The puzzle as a whole has six orientations that are considered
identical, so there really only 7!·66=235,146,240 ways
of putting the pieces back into its box. As is so often the case with
puzzles like this, that number is not really representative of its
difficulty. The orientations are all forced because each newly placed
piece has to match at least one other, so there are certainly
no more than 7!=5040 positions to check when solving it. In fact most of these
positions fail to match its colours well before you place the seventh piece,
the actual number is far less.
The Circus Puzzler has three pairs of identical pieces which
can be swapped without changing the position, so that version has no more than
7!/23=630 positions.
Thinkominos similarly has 6!·65/3 = 1,866,240 ways of
packing the pieces onto the box, but realistically has no more than 6!=720
positions to check.
I have not found any pattern in the numbers on Drive Ya Nuts or the colours of the Circus Seven, so it seems that the only way to find the unique solution is to try all possibilities.
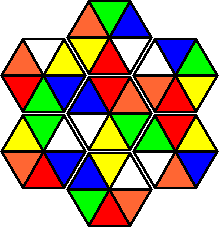
The Circus Puzzler has three pairs of identical pieces. It stands to reason that the piece that occurs only once has to be in the centre, and that each pair goes on opposite sides of the centre piece. This leaves only very few possibilities, and the two solutions shown below are then very quickly found. These are the only solutions.
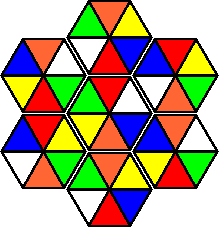
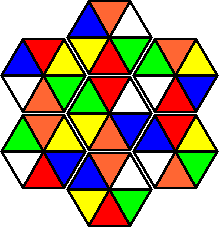
All the listed colour variations have unique solutions.
Variation A: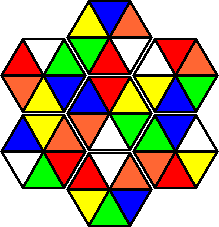 |
Variation B: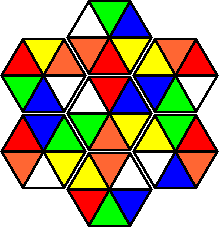 |
Variation C: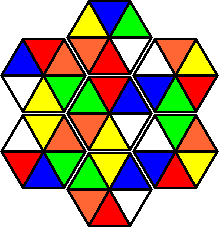 |
Variation D: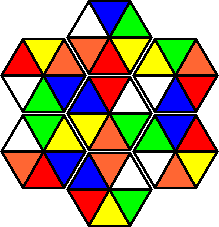 |
Variation E: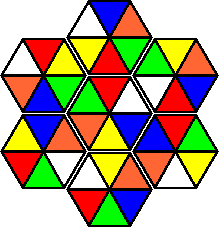 |
Variation F: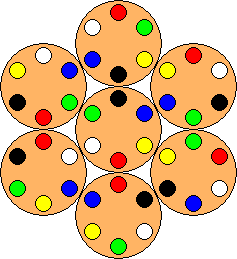 |
The Thinkominos puzzle has two solutions. There does not seem to be a pattern so the only way to solve it is to just try all combinations.