Jaap's Puzzle Page

Cohan Circle / Arusloky

Cohan Circle Arusloky

The Cohan Circle consists of two overlapping circular discs. The distance between the centres is exactly one radius length. The discs are made up of many pieces with curved sides, which allow them to be rotated any number of 1/6th turns. Each disc has 6 blank triangles, and 12 petal-shaped pieces. As some pieces are shared between the two discs, there are all together 10 triangles and 19 petals.

The 19 petals come in 4 colours - 6 red, 6 green, 6 blue, and 1 white. The aim is to make the 6 peripheral pieces of each disc of a single colour, forming two circles, and also place the white piece in the centre.

This puzzle was invented and patented by Hooshang Cohan, number US 4,580,783 published 8 April 1986. It may have been sold as the 'Magic Circle Puzzle', as the solution booklet has that title covered by a label with the correct name.

Arusloky is a recent version of this puzzle, made in Spain. It has a slightly different colour scheme, with 6 red petals, 6 yellow petals, and everything else blue. Its starting configuration has a red and a yellow circle.

If your browser supports it, you can click on the link below to play with a Javascript version of both the Cohan Circle and Arusloky.

Javascript Cohan Circle / Arusloky

Links to other useful pages:

Arusloky homepage. You can order the puzzle from here.

The number of positions:

There are 19 coloured pieces, so there are at most 19! positions. This limit is not reached because The Cohan Circle has three sets of six indistinguishable pieces. This leaves only 19!/6!3 = 325,909,584 positions. If you consider the three coloured sets to be equivalent, then you can divide by a further 3! to get 54,318,264 positions.
Arusloky has two sets of six and one set of seven indistinguishable pieces. It therefore has 19! / (6!2·7!) = 46,558,512 positions.

I have used a computer to calculate God's algorithm for the Cohan Circle. This first table shows the results if the two circles may be any colour. Any position can be solved in at most 14 moves (10.892 on average), or 20 (16.447 on average) if every 1/6 of a turn is counted as a separate move.

Face turn metric
S
i
x
t
h

t
u
r
n

m
e
t
r
i
c		 01234567891011121314Total
066
12424
2244872
3129696204
496288192576
5484327683601,608
6123841,5361,9206724,524
72161,9204,8004,5121,34412,792
8721,6567,65613,77610,3682,68836,216
968888,47226,83237,41623,2925,220102,126
102886,74437,05685,90896,98451,7689,120287,868
11483,81638,160141,492260,832248,160105,92411,448809,880
121,39228,188177,636506,928778,632607,140159,1564,8002,263,872
1326415,624168,576759,7921,800,4322,286,2881,119,54086,4001206,237,036
14485,904122,160887,7003,250,2726,454,8305,176,068709,4162,49616,608,894
151,56063,696789,7084,544,27414,003,77217,464,7283,783,36025,16440,676,262
1626422,056471,3844,445,14821,498,66041,519,52013,868,748160,13481,985,914
17243,672149,3522,358,98418,030,23456,024,25030,471,336609,20424107,647,080
1816815,528430,6445,324,60427,410,35826,806,1641,134,5644861,122,078
1926412,372281,9522,435,4064,791,876509,670248,031,564
2056412,02452,13416,26680,988
Total6603001,4947,29635,472172,572834,4923,964,45217,925,90668,603,088151,332,49880,574,2342,457,61896325,909,584

This table shows the results if the circles must have particular colours. Any position can be solved in at most 17 moves (12.230 on average), or 23 (18.339 on average) if every 1/6 of a turn is counted as a separate move.

Face turn metric
S
i
x
t
h

t
u
r
n

m
e
t
r
i
c		 01234567891011121314151617Total
011
144
24812
32161634
416483296
587212860268
6264256320112754
7363208007522242,132
8122761,2762,2961,7284486,036
911481,4124,4726,2283,88288617,029
10481,1246,17614,27416,1208,6161,69248,050
1186366,35623,45842,96640,72018,4782,824135,446
122324,69829,35082,436124,54099,91836,0403,412380,626
13442,59227,720121,962277,178351,736228,02052,5242,1241,063,900
14897620,198140,820479,742917,036949,630393,29837,8324522,939,992
1527610,922126,848659,9861,881,5532,944,0681,957,096333,1587,508407,921,455
16524,15683,990705,6703,058,2007,133,6727,192,3551,946,76872,65228620,197,801
17891637,364535,0823,650,05013,005,94019,870,4468,252,463477,2952,534445,832,102
18928,816235,2942,683,63715,260,69637,434,23224,801,5552,247,13616,5101282,687,980
1972444,184914,1648,785,58037,350,46044,032,0826,982,22481,0802498,190,522
20202,500100,5761,698,98213,116,08031,080,47810,325,245247,0169056,570,987
21201,88461,496884,1784,605,3713,867,105267,43618819,687,679
22923,29447,380135,16240,391109226,428
2312761602250
Total110502491,2165,91228,766139,266666,3963,114,41813,678,92450,107,040118,257,375115,139,22324,114,855655,4534291325,909,584

The single position that takes 17 face turns is L R' L R' L R2 L2 R L' R L' R' L2 R4 L' R4 L, which has the two circle colours swapped.

Here are the results for the Arusloky. This first table shows the results if the two circle colours may be swapped so there are two solutions. Any position can be solved in at most 14 moves (10.556 on average), or 20 (15.763 on average) if every 1/6 of a turn is counted as a separate move.

Face turn metric
S
i
x
t
h

t
u
r
n

m
e
t
r
i
c		 01234567891011121314Total
0:22
1:88
2:81624
3:4323268
4:329664192
5:16144256120536
6:41205126362241,496
7:726081,5761,4884484,192
8:164962,3484,5203,47284011,692
9:22322,5448,46412,3007,6681,57232,782
10:561,89611,22027,52432,16016,1362,37691,368
11:888810,71644,05285,03280,86429,2602,240253,060
12:2887,43252,244162,592256,720177,91233,772592691,552
13:483,82446,584235,762591,050694,446249,48011,39281,832,594
14:1,14429,972253,2961,023,0981,953,8221,173,93493,4701604,528,896
15:20811,748184,5481,245,3603,890,7923,779,374484,2641,7929,598,086
16:242,35672,648875,0364,595,9567,487,2461,607,8409,54614,650,652
17:17611,992253,3482,253,8126,564,9722,629,03031,30011,744,630
18:844017,044265,4961,447,5561,237,33035,8843,003,758
19:1203,05233,62269,8586,1586112,816
20:8285616108
Total:2201004822,23210,34449,264230,8841,046,9784,360,34813,866,93220,772,2246,133,83284,864646,558,512

And finally, this table shows the results if the Arusloky has only one solved position. This can be reached from any position in at most 15 moves (11.223 on average), or 22 (16.657 on average) if every 1/6 of a turn is counted as a separate move.

Face turn metric
S
i
x
t
h

t
u
r
n

m
e
t
r
i
c		 0123456789101112131415Total
0:11
1:44
2:4812
3:2161634
4:16483296
5:87212860268
6:260256318112748
7:363047887442242,096
8:82481,1742,2601,7364205,846
9:11161,2724,2326,1503,83478616,391
10:289485,61013,75816,0728,0641,20845,688
11:44445,35822,02242,44240,25814,7501,348126,626
12:1443,71626,11080,992127,02488,64619,282728346,642
13:241,91223,264117,171289,206338,453140,38913,072196923,687
14:57214,974125,532495,119927,789650,840111,6703,338162,329,850
15:1045,87891,974603,4141,831,2402,107,752614,30829,0322165,283,918
16:121,21837,564448,1792,324,3224,591,7192,299,538180,0771,96249,884,595
17:1047,200162,2481,522,5605,615,7445,304,343741,55311,6723213,365,456
18:451220,669382,8222,791,6645,621,0941,675,96047,07019010,539,985
19:869423,010352,8981,660,6111,283,15492,7167623,413,853
20:41164,71461,760158,71343,429964269,700
21:21021,0571,6262243,011
22:235
Total:110502411,1165,17224,632115,442523,7212,195,6657,454,91616,276,35215,687,2264,073,080198,7092,17946,558,512

Notation:

Let a clockwise 60 degree rotation of the left disc be denoted by L. Rotations of 120, 180, 240, 300 degrees are then denoted by L2, L3, L4 and L5. Note that L5 can also be considered an anti-clockwise 60 degree turn, and is therefore also denoted by L'. Turns of the right disc are denoted in the same way, but using the letter R.

Terminology:

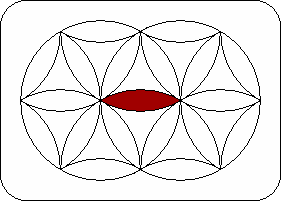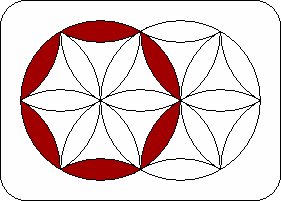
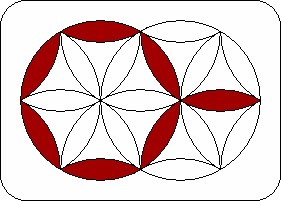
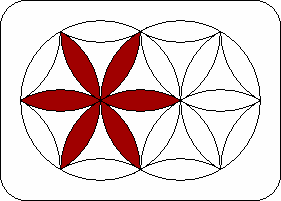
The left circle is the 6 piece locations that lie on the rim of the left disk. Eventually all the pieces of one colour will be placed in the left circle. Similarly, the right circle is the 6 locations on the rim of the right disk, which will be made another colour. The left extended circle is the left circle plus the horizontal piece location at the right hand side. Note that the 7 pieces in the left extended circle will remain in the left extended circle if you do R2, R4, or L moves. Similarly the right extended circle is the right circle plus the left horizontal piece location. The spokes of the left disk are the six locations of the left disk that meet in the centre, i.e. those locations that lie inside the left circle. Similarly the spokes of the right disk are the six locations that meet in the centre of the right disk. The middle is the central horizontal location where the white piece should be when the puzzle is solved. Note that this is a left spoke as well as a right spoke.

Solution:

Phase 1: Put the green/yellow pieces in the left extended circle.

  1. Try to put as many green (Cohan Circle) or yellow (Arusloky) pieces in the left extended circle as you can before doing the steps below.
  2. Find any green/yellow piece that is not yet in the left extended circle.
  3. By doing one of the following steps, move the green/yellow piece so that it becomes the top right spoke of the right disk:
    1. If it is one of the left spokes, turn the left disk so that the piece is in the middle, and then do R2.
    2. If it is the bottom right spoke of the right disk, then do R4.
    3. If it lies in the right circle, then do R2 or R4 to bring the piece into the left disk, and do step 1.
  4. Turn the left disc so that a non-green/non-yellow piece lies at the top right of the left circle (the top left spoke of the right disk).
  5. Do R3 L2 R L4 R' L2 R to insert the green/yellow piece into the left extended circle.
  6. Repeat b-e for the remaining green/yellow pieces.
  7. The left extended circle now contains six green/yellow pieces and one of another colour. If this seventh piece is red, then use steps b-e to place any blue in the left extended circle in place of the red one.

Phase 2: Put the red pieces in their extended circle.

  1. Turn the puzzle around, so that the green/yellow pieces are now in the right extended circle. In the steps below, the red pieces will be placed in the left extended circle in much the same way as the green/yellow ones were in phase 1.
  2. Try to put as many red pieces in the left circle as you can without disturbing the green/yellow pieces from the right extended circle. Note that if you use only L2, L4, and moves of the right disk then the green/yellows will be safe.
  3. Find any red piece that is not yet in the left extended circle.
  4. By doing one of the following steps, move the red piece so that it becomes the top right spoke of the right disk:
    If the red piece is one of the left spokes, turn the left disk so that the piece is in the middle, and then do R2.
    If the red piece is the bottom right spoke of the right disk, then do R4 so that it becomes the top right spoke.
  5. If necessary do L2 or L4 so that a non-red piece lies at the top right or bottom right of the left circle (the top-left/bottom-left spoke of the right disk).
  6. If a non-red piece lies at the top right of the left circle, then do R3 L2 R L4 R' L2 R to insert the red piece there.
  7. If a non-red piece lies at the bottom right of the left circle, then do L2 R2 L4 followed by R3 L4 R' L2 R L4 R' to insert the red piece. Note that the first three moves put the red piece at the bottom right spoke of the right disk, and the rest of the sequence is the mirror image of the sequence of step f.
  8. Repeat c-g for the remaining red pieces.

Phase 3: Make the circles.

  1. Find the non-red piece in the left extended circle. If it is not one of the spokes of the right disk, then do L2 or L4 to make it so.
  2. If necessary, do R2 or R4 so that the left circle is completely red.
  3. Find the non-green piece in the right extended circle.
  4. If it is at a left spoke, then a L2 or L4 turn will complete the green circle, otherwise do one of the following, depending on where in the right circle it lies:
    Top: R2 L4 R2 L2 R4
    Top right: R2 L2 R2 L4 R4
    Bottom right: R4 L4 R4 L2 R2
    Bottom: R4 L2 R4 L4 R2

Phase 4: Place the white petal in the centre.

  1. If the white piece is in the left disk, then turn the puzzle around so that it lies in the right disk.
  2. Depending on which spoke the white piece lies at, do one of the following:
    Top right: L2 R2 L2 R4 L4 R4
    Right: R L4 R L4 R2 L4 R L4 R
    Bottom right: L4 R4 L4 R2 L2 R2

Other neat sequences:

Start position.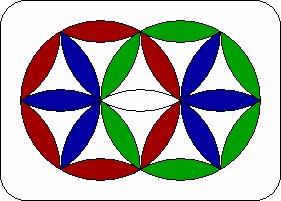
1. Swap circles. L R L4 R L R' L R' L' R2 L4 R L' R L' R L' R' 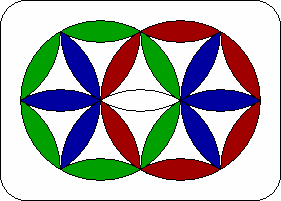L' R' L R' L R' L2 R4 L2 R2 L' R' L4 R' L
2. Swap right circle with spokes. L R' L R4 L R L' R L R L R L3 R' L'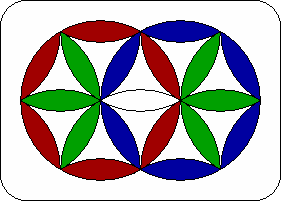
3. Wagonwheel. R L' R' L R L2 R3 L2 R' L3 R L R 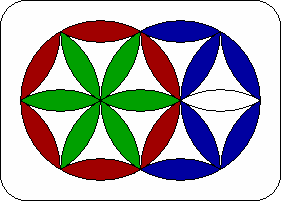L' R' L4 R3 L2 R L2 R4 L R2
4. Pacman. R' L R4 L' R L3 R' L R3 L4 R3 L4 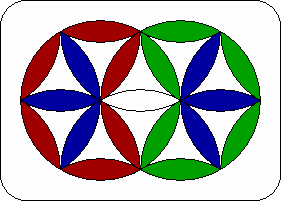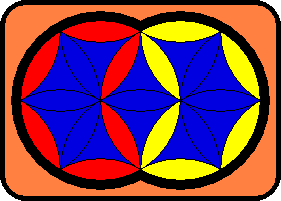L' R4 L R' L R' L2 R4 L R4 L2
5. Hourglass. R L R2 L R' L2 R2 L2 R' L R3 L' R L4 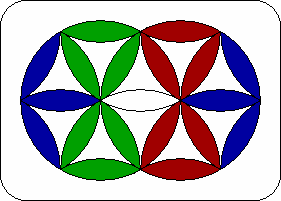R3 L4 R L' R L4 R4 L R' L R' L R2 L4
6. Fish. L' R' L R' L R L R L' R' L R2 L' R3 L3 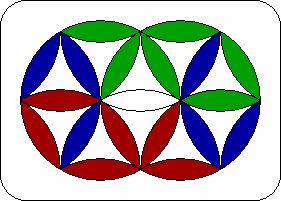L R L' R L R' L4 R' L R L R L4 R4