Jaap's Puzzle Page

Cubedron / Cybedron

Cubedron Cybedron

The Cubedron is a puzzle consisting of a transparent ball containing only 5 pieces. The pieces are square pyramids that together form a cube. Each piece is one face of the cube, and the top face of the cube is missing. By tilting the ball, any of the side pieces can be shifted into the empty spot.

Cubedron tiles

The Cubedron has faces where the edges have four different colours, and the pieces are supposed to be placed so that where two pieces share an edge, their colours should match. All pieces use the same four colours but in a different orders so that the pieces are all unique. There are six possible unique tiles with four colours, and the puzzle simply uses five of them. There are two solutions, but only one is reachable without using dexterity.

Cybedron tile

The Cybedron is a variation of the Cubedron which has identical pieces with only two colours. It has two solutions, both reachable without any dexterity skills.


The puzzle was designed and patented by Pantazis Houlis, WO 2010/064994, published 10 June 2010.

If your browser supports JavaScript, then you can play the Cubedron or Cybedron by clicking the link below:

JavaScript Cubedron/Cybedron

The number of positions:

The cubedron has 5 pieces, each with 4 orientations. This leads to a maximum of 5! permutations and 45 orientations, and so to a maximum of 5! ·45 = 122,880 positions. This limit is not reached because:

This leaves 5! ·45/8 = 15,360 positions. There is only one reachable solution. The second solution can only be reached by doing a single quarter twist of a piece, and so cannot be done except by some dextrous manipulation of the puzzle.

The cybedron has 5 pieces which are all identical so only orientations matter, leading to a maximum of 45 = 1,024 positions. This time an apparent single quarter turn is possible, although that involves invisibly swapping some pieces around. The orientation of the puzzle as a whole does not matter, leading to 45/4 = 256 distinct positions. There are two solutions, both reachable.

A computer search gave the following results:
Cubedron
MovesPositions
01
14
212
336
4108
5320
6898
72118
84030
94894
102350
11534
1250
134
141
Total:15360
Avg Depth:8.3794
Cybedron, 1 solution
MovesPositions
01
14
212
334
476
5102
627
Total:256
Avg Depth:4.3203
Cybedron, 2 solutions
MovesPositions
02
18
224
354
491
568
69
Total:256
Avg Depth:3.8125

This shows that on the Cubedron any position can be solved in at most 14 moves, and on the Cybedron at most 6 moves whether you want a particular solved position or don't care which of the two solutions is reached.

Links to other useful pages:

MindStrat puzzles is the maker of this puzzle.

Notation:

Suppose you tilt the puzzle upwards so that the front tile goes over the top and falls down to become the back face. That move will be denoted by the letter F. Similarly the letters L, B, and R denote moves where the Left, Back, or Right tile moves over the top to the other side.

Solution:

Cubedron solutions Cybedron solutions
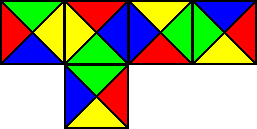Cubedron solution 1 Cybedron solution 1
Cubedron solution 2 Cybedron solution 2

The two solutions are shown above. On the Cubedron the second solution has all the pieces in the same place as the first solution, but they are all rotated a quarter turn clockwise. The two solutions on the Cybedron are identical except that the two colours have been exchanged.

Cubedron:

  1. Solve the bottom face. Simply tilt the puzzle so that the correct piece is on the bottom. You can determine which tile belongs on the bottom face as follows:
    1. Choose two colours, say yellow and green.
    2. There are three ways the two colours could be arranged on a tile - yellow to the left of green, yellow to the right of green, and yellow opposite green. Count how many there are of these three types.
    3. The tile that is unique in its placement of the two colours is the one that belongs on the bottom face. On the standard arrangment above, there is only one tile that has yellow opposite green so that should be the bottom tile.
  2. Solve the front tile. The are two tiles that can fit. The other two tiles will not work because if you were to put one in front and rotate it so that its bottom edge matches the bottom face then it will show the same colour on the left or right side as the bottom face has. This would mean the left or right face has to edges of the same colour. Once you have decided which tile to put at the front, solve it as follows:
    1. Bring the tile to the front position, without caring about the orientation. This is easy to do without disturbing the bottom face.
    2. If the front tile is correctly oriented (i.e. its bottom edge colour matches with the bottom face) then you are done.
    3. Move the front tile upwards, the right tile to the front, and the first tile to the right. This swaps the front and right tiles. In our notation this is F R B followed by rotating the whole puzzle to the right so that the front tile ends up on the right.
    4. Repeat step 3, to again swap the front and right tiles. The combined effect is that the tiles haven't moved position, but that the front and right tiles have both been twisted clockwise a quarter turn.
    5. If the front tile is still not correctly oriented, repeat steps 3 and 4 until it is.
  3. Rotate the whole puzzle to the left, so that the solved tiles are on the left and bottom.
  4. Solve the front tile. This is done in exactly the same way as step b, but you must take care not to disturb the left or bottom faces.
  5. Rotate the whole puzzle to the left, so that the solved tiles are on the left, back and bottom.
  6. Solve the front tile. This is again done in exactly the same way as step b, but you must take care not to disturb the left, back or bottom faces.
  7. Rotate the whole puzzle to the left, so that the only unsolved face is at the front.
  8. If the front face needs a quarter turn in either direction then the solution you are aiming for is not possible. Instead look at the four other faces and decide whether the other solution can be reached by giving them a clockwise quarter turn, or by an anti-clockwise quarter turn. Then, with the unsolved piece in front again, do one of the following:
    Clockwise: RBRB LF RBRB LF
    Anti-clockwise: LBLB RF LBLB RF
    The front tile might now still need a half turn.
  9. To give the front tile a half turn, do RFR BBBB LFL.

Cybedron:

  1. Choose one of the two colours. For the rest of this solution I will assume you chose blue but if you use red everywhere instead then you will get the other solved position.
  2. Hold the puzzle such that the blue edges of the bottom face are at the front and the right.
  3. Solve the front tile so that its blue edges are at the bottom and on the right. If it is not yet correctly oriented, then do the following:
    1. Move the front tile upwards, the right tile to the front, and the first tile to the right. This swaps the front and right tiles. In our notation this is F R B followed by rotating the whole puzzle to the right so that the front tile ends up on the right.
    2. If the new front tile is also not correctly oriented, repeat step 1 until it is correct.
  4. Rotate the whole puzzle to the left, so that the solved tiles are on the left and bottom.
  5. Solve the front tile. This is done in exactly the same way as step b. This results in a blue bottom left corner.
  6. There are now two unsolved tiles. Alternate moving one and then the other until at least one of them is solved.
  7. If the last tile seemingly needs a quarter turn to be solved, then move that tile. It will now either be solved or need a half turn.
  8. If the last tile needs a half turn, then hold the puzzle with that tile in front. If the blue corner of the cube lies at the back left then do LBLBLL, but if the blue corner is at the back right do the mirror image of that, namely RBRBRR.

Nice move sequences:

  1. To swap solutions on the Cybedron, do FRF FRFRF FR.
  2. For a shorter way to swap solutions on the Cybedron, hold it with the monochrome corner at the front bottom right, and do FLFLF.
  3. To rotate the four sides clockwise a quarter turn, do FRBLFR FRBLFR. This can be used on the Cubedron to go from one solution to the other, provided you can also somehow twist the bottom face. This can be done by tilting the puzzle slightly, and rotating it around the main axis. The amount of play between the side tiles causes them to creep forward slightly, so that after a while it is as if the bottom face has turned a quarter turn in the opposite direction.