Dino Cube / Rainbow Cube / Brain Twist

The Dino Cube is a cube shaped puzzle, and like the Skewb, it has eight axes of rotation centred around the corners. Its cutting planes go diagonally through the square faces, cutting off triangular pyramidal corners. There are twelve moving pieces, one on each edge of the cube. It is called a dino cube because it originally had pictures of dinosaurs on the sides. Versions with 6 colours (pictured above) were also made, as well as with only 4 or 2 colours.
Recently new versions of this puzzle were made, some with a pillowed cube shape, either stickered with 6 colours, or using two or three colours of plastic.

The second puzzle pictured above is the Rainbow Cube. It has the shape of a cuboctahedron. It is very much like a Dino Cube in which the corners have been cut off, giving it 8 triangular faces as well as 6 square ones. The puzzle still has only 12 moving pieces, but now there are also stationary centres in the triangular faces. There are two colour schemes. One has 14 colours, the other has only 7 colours with opposite faces the same colour. As the puzzle with the 7 colour scheme does not have any identical pieces, the two colour schemes give puzzles of the same difficulty.

The Brain Twist is a puzzle by Hoberman. The third picture above shows what it looks like when unfolded in its star shape. To make a move, the points of the star are pushed together causing it to fold into a tetrahedron shape, after which the four corners of the tetrahedron can be twisted. You can unfold it and then fold it in the other direction to get a different tetrahedron with four new corners to twist. The equivalence with the dino cube is most easily seen when the puzzle is in its star shape, and imagining the effect of a twist of three pieces around a corner.
There are two solution patterns - one with each tetrahedron face a single colour, and one with each tetrahedron corner a single colour. The second solution does not look as nice when in star shape however.
It was patented by Charles Hoberman and Matthew Davis on 12 May 2005, US 2005/098947.

Jackpot, also known as Platypus, is a puzzle from Meffert's, and the fourth picture above shows a prototype version. Unlike most of the other puzzles on this page, on the Jackpot the eight axes are not identical. It is not cube shaped but is based on the tetrahedron, with the corners extended in a triangular cylindrical shape. There are four large hexagonal faces, marked with card suits, as well as four small triangular faces, marked with J, Q, K, and A card values. The pieces are all similarly marked on their sides. For an extra challenge, on some versions of the Jackpot the hexagonal faces also have coloured marks along their edges, so that their orientations matter.
It was patented by Yusuf Seyhan on 16 January 2003, WO 03/004117.

There is also another puzzle that is equivalent to the Dino Cube, but I do not know much about it. Colloquially known as the Dino Star, it is in the shape of a Stella Octangula, of which the corners can rotate. There are small pieces in between them along the edges of the internal octahedron, and the three pieces around each tip form a circle on the surfaces of the adjacent tips. Each circle should be of one colour. I first saw one in David Singmaster's collection. Most have a body of a single colour (various colours were available), but there are some where each tip has its own colour.

The Dinomorphix is a pillowed tetrahedral version of the puzzle designed by Traiphum. It has only 4 triangular face centres. In the version with plastic of various colours, the face centres are left white,, and it has three pieces of each of the other colours. It is equivalent to the 4-colour dino cube, and it can be solved so that each face has just one colour, or so each tip has one colour. The stickered version also has stickers on the four centres, so has only the faces solution.

The Twist Ball is a spherical version of the Dino Cube. It comes in various designs and colour schemes. In some of the designs (such as the flower, rings, spiral, or square designs) the orientations of all the centres are visible, giving them the largest possible number of positions in this family of puzzles. The Basketball design is very interesting as it can be solved in three different orientations.

The number of positions:

There are 12 moving 'edge' pieces, which seemingly have 2 possible orientations. It is however impossible to flip any piece. Furthermore, every move is an even permutation (a 3-cycle) so the moving pieces can be permuted in 12!/2 ways. Versions with identical edge pieces will of course fewer distinguishable edge positions than that. Centres with visible orientation, if the puzzle has them, can be twisted independently of the rest of the puzzle. Therefore each such centre multiplies the number of distinct positions by a factor of 3. The table below shows the number of states the various puzzles in the dino-cube family have.

	Edges		Centres		Core		Approximate	Actual
Dino Cube 6-colour	12!/2	*	1	/	12	=	19,958,400	19,958,400
Dino Cube 4-colour	12!/3!⁴	*	1	/	24	=	15,400	15,408^*
Dino Cube 3-colour	12!/4!³	*	1	/	24	=	1,443.75	1,479^*
Dino Cube 2-colour	12!/6!²	*	1	/	24	=	38.5	48^*
Dino star	12!/2	*	1	/	12	=	19,958,400	19,958,400
Dino star 8-colour	12!/2	*	1	/	1	=	239,500,800	239,500,800
Braintwist	12!/2	*	1	/	12	=	19,958,400	19,958,400
Rainbow Cube	12!/2	*	1	/	1	=	239,500,800	239,500,800
Jackpot	12!/2	*	1	/	1	=	239,500,800	239,500,800
Jackpot with centres	12!/2	*	3⁴	/	1	=	19,399,564,800	19,399,564,800
Dinomorphix	12!/3!⁴	*	1	/	12	=	30,800	30,816^*
Dinomorphix stickered	12!/3!⁴	*	1	/	1	=	369,600	369,600
Twistball Basketball	12!/4!³	*	3⁸	/	12	=	18,944,887.5	18,946,710^*
Twistball Flower	12!/2	*	3⁸	/	1	=	1,571,364,748,800	1,571,364,748,800

As the Jackpot and Dinomorphix versions show, this puzzle is actually based on tetrahedral symmetry. This is why, even if the puzzle has a cube shape, the edges cannot be flipped. On a Jackpot or Dinomorphix a piece flip would change the shape of the puzzle, and none of the moves change the shape. If the puzzle has no centres, or the centres are all the same, then the core of the puzzle can be in any of the 12 orientations that a tetrahedron has. However, on a cube-shaped puzzle in which the edges do not have a visible orientation, it is not possible to see if all edges are flipped, so the core can be in any of 24 orientations.

The numbers in the table marked with an asterisk ^* had to be calculated using Burnside's Lemma. Some of the positions have symmetry, and so do not give 12 (or 24) different patterns in the 12 (or 24) different puzzle orientations, but fewer. Simply dividing all permutations by the puzzle orientations ignores that fact, and so will give an underestimate of the actual number of distinct positions.

The 6-colour Dino Cube actually has two solutions, which are mirror images of each other. This is similar to the two solutions (faces or tips) of the Brain Twist. The unstickered Dinomorphix not only has a face solution and the tip solution, but on each of those the colour arrangement can also be done in mirror image.

I have calculated how many moves each position of the Dino Cube needs to solve, as shown in the table below. The first column was calculated with the assumption that there are two solutions (mirror images of each other), the second column is based on the assumption that you want a particular one of those. The Rainbow cube was first calculated by Claude Crépeau and Thanh Vinh Nguyen, and is shown in the third column.

Moves	Dino / Brain Twist 2 Solutions	Dino / Brain Twist 1 Solution	Rainbow Cube Jackpot (no colours)	Dino Cube 2-colour	Dino Cube 3-colour	Dino Cube 4-colour	Dinomorphix Unstickered	Dinomorphix Stickered
0	2	1	1	1	1	2	2	1
1	32	16	16	1	2	16	16	8
2	320	160	160	6	15	144	144	72
3	2,816	1,408	1,408	18	62	1,120	1,120	560
4	23,424	11,712	11,712	21	264	5,870	6,804	3,642
5	180,084	90,912	90,912	1	702	7,728	17,988	19,470
6	1,227,084	640,192	644,756		418	516	4,716	74,184
7	6,167,660	3,740,838	4,070,826		15	12	26	153,339
8	10,926,002	11,138,597	21,433,009					106,923
9	1,429,972	4,313,963	76,410,122					11,337
10	1,004	20,577	109,897,795					64
11		24	26,611,502
12			328,215
13			366
Total	19,958,400	19,958,400	239,500,800	48	1,479	15,408	30,816	369,600

Avg Depth	7.6072	7.9502	9.5518	3.25	5.0014	4.4759	4.8448	7.0083

In Sloane's On-Line Encyclopedia of Integer Sequences the first three are included as sequences A079766, A079767, and A079768.

Solution:

These are generally very easy puzzles to solve. There is really only one easy sequence of moves that you need to be able to do. Consider two adjacent axes on the puzzle, with the five piece positions they contain numbered as shown here:

1 2

3

4 5

You are trying to put the correct pieces at positions 1 and 2, and you haven't yet solved 3, 4 and 5 yet (though it is quite possible that one or more of them happen to be correct, ignore them).
Solving the first piece, at position 1 is trivial, since you can just put it there without disturbing previously solved pieces.
Next, you want to put the correct piece at position 2, without disturbing the piece at 1.

First bring the piece belonging at 2 to position 4 or 5, without disturbing any of the pieces you have previously solved.
Then turn the top face/corner clockwise, putting the piece that currently is at position 2 to the intersection at position 3.
Turn the bottom face/corner to bring the piece belonging at 2 to position 3, replacing the old piece.
Turn the top face/corner anti-clockwise, back to its previous position, which puts the correct pieces at both 1 and 2.

Once you understand this simple technique, the puzzle can be easily solved by solving the pieces in the following order:

Solve three adjacent pieces that share an axis (a triangular face in the Rainbow Cube, three pieces at one corner in the Dino Cube, etc).
Solve the six pieces that are adjacent to the first three you solved. You need not move any of the first three solved pieces at all.
Solve the last three pieces (which are the ones directly opposite the first three). This is trivial, as you only need at most a single move to do this (though see note below).

Sometimes however it is hard to recognise which piece belongs where. On the 7-colour Rainbow Cube each colour is used on opposite faces of the puzzle, which means that each piece also has a mirror image twin. If you just keep track only of the colours of the triangular faces, then you cannot go wrong as the mirror piece will have its colours swapped if you try to use it instead. On the Dino Cube adjacent pieces have only one colour in common, so it seems that you could put the wrong pieces next to each other. This is not the case however - if you try to place the wrong piece, it will seem to be flipped.

On the Brain Twist it is easy to get confused because of the constant need to flip the puzzle inside out, but this puzzle has another neat twist in store. It may happen that you solve the puzzle completely but for two pieces that need to be swapped. This is unfortunately not possible (it is an odd permutation and every move is an even permutation). What has happened is that you have built the colour pattern in mirror image. You have to practically re-solve the whole puzzle - choose any face you had solved, swap two of its pieces, and continue from there.

If you have a puzzle on which the face orientations are visible, then the techniques outlined above are not quite sufficient. With a little care you can ensure the face orientations are correct on all but the last face (step c above). If you are solving a Jackpot where the hexagonal faces are marked, then you can simply leave an unmarked triangular face till last instead. If X and Y are moves on adjacent axes, then the move sequence Y X Y' X Y X Y' X twists the face centre on axis X anti-clockwise one step.

Pretty Patterns and other moves:

Spot Patterns

The rainbow cube has two types of spot patterns, patterns in which only the triangular centres have a different colour. One has 8 spots, the other only 6 spots.

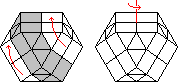The 8 spot is made like this: Hold the puzzle with a square on top. Make a slice move, i.e. turn any triangular face clockwise, and its opposite face anti-clockwise (so the two faces have actually moved as a unit). Turn the whole puzzle a quarter turn around the vertical axis. Repeat this a number of times. After 6 or 10 times (depending on the direction you turn the puzzle) you will get the 8 spot.

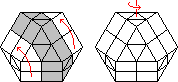The 6 spot is done much the same way, except that a triangular face is on top, the slice move is done on any of the other faces, and the puzzle is rotated through 120 degrees each time. After doing this 8 or 10 times, depending on the direction, the 6 spot will appear.

Swapping between solutions

The Dino Cube has two solutions which are mirror images of each other. To change a solved Dino Cube to show the other solution, perform the following move sequence:
urb urf urb' ulf urf drb' urb' ulb dlb' dlf.
There is a longer method which is much easier to remember:
(urb ulf drf dlb) (urf' ulb' drb' dlf') (urb ulf drf dlb).
This first turns one tetrad of corners clockwise, then the other tetrad counter-clockwise, and then the first tetrad clockwise again.
The same method works on the Brain Twist to swap from the faces-solution to the corners-solution, and vice versa. Simply twist all corners clockwise, flip it, twist all corners counter-clockwise, flip again, and turn all corners clockwise.

Jaap's Puzzle Page