Jaap's Puzzle Page

Dodeca Nona

Dodeca Nona

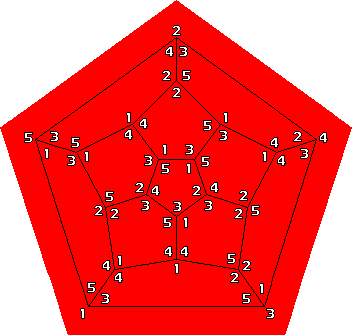
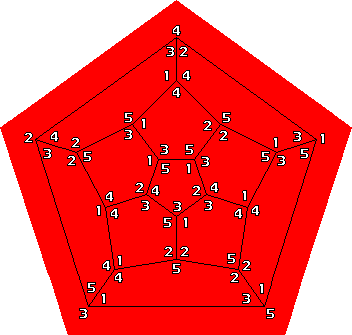
The Dodeca Nona puzzle by Hanayama Toys is a metal dodecahedron with twelve magnetic pentagonal tiles. Every tile has the numbers 1 to 5 arranged in some order at the corners. There are 4!=24 such arrangements, and these all occur on the sides of the 12 tiles. The opposite sides of each tile corner has the same number, so that the arrangements on the two sides of a tile are mirror images. The aim is to place the tiles on the dodecahedron so that every vertex has three numbers that add up to 9.

The number of positions:

There are 12! ways to distribute the tiles on the dodecahedron faces. Each tile then has 5·2 ways to orient it. This gives 12!·1012 = 479,001,600,000,000,000,000 positions. To discount rotations of the dodecahedron, divide by 60 to get 7,983,360,000,000,000,000. Taking the mirror image is also possible (every tile can be placed upside down on the opposite side), so you can divide by 2 for a final number of 3,991,680,000,000,000,000 positions. Most of these are nowhere near solutions, as the first few placed tiles already give sums other than 9. This number therefore does not really indicate the difficulty of the puzzle. However, of this huge number only 1122 are solutions, so it is nevertheless very difficult.

Links to other useful pages:

Math Games article by Ed Pegg about the late Nob Yoshigahara, has some nice background information about this puzzle and others he has invented.

Solution:

I don't know of any good way to solve this puzzle other than trial and error, or a brute force computer search. In the Math Games article, it is mentioned that Harry Nelson used a supercomputer to find all solutions, which took 26 minutes. I assume this was in the late 70s. It now takes only seconds on a standard PC to do the same thing.

There are five ways to sum to nine: 1+3+5, 1+4+4, 2+3+4, 2+2+5, or 3+3+3. It is not possible to have distinct numbers at each vertex (i.e. 1+3+5 or 2+3+4) because there are twelve 3's but 20 vertices. It is possible for the vertices two opposite faces to have distinct numbers. There are two solutions to this:

Dodeca Nona solution Dodeca Nona solution