1. Sets and functions

A set is a collection of things called elements, and each of these elements occurs at most once in a set. A (finite) set can be given explicitly as a list inside a pair of curly brackets, for example {2,4,6,8} is the set of even positive integers below 10. It has four elements. There are infinite sets - sets that have an infinite number of elements - such as the set of integers, but I will generally discuss only finite sets (and groups) here.

On puzzles, we will often consider the set of puzzle positions.

A function f:AB from set A to set B is a pairing that assigns to each element in A some element of B. Set A is called the domain and set B the range. If the function f assigns element b to a then we say that f maps a to b, and call b the image of a. We could write this as f(a)=b, but I prefer to write it as af=b. Writing f on the right like this will also be more natural in the cube context later, but be aware that in many books it is written on the left instead.

A move on a puzzle is usually a function on the set of positions. A move applied to one position results in another position. This assumes however that a move can always be applied to any position - in some puzzles such as the Square-1 this is not the case and makes such a puzzle much harder to analyse.

A function is injective or one-to-one if the function maps different elements in A to different elements in B.
A function is surjective or onto if every element in B is mapped to by the function.
A function is called a bijection if it is both one-to-one and onto.

Lemma 1.1: For a bijection f:AB we can uniquely define a function g:BA, such that if a is any element of A and b is its image in B under f (i.e. af=b) then bg=a.
Proof: Let b be an element of B. Since f is onto, there must be some a in A such that af=b. Since f is one-to-one, this element a is uniquely determined. Therefore it is actually possible to simply define g as that pairing that maps b to a whenever f maps a to b.

The function above is called the inverse function of f, and is usually denoted by f ^-1. Thus every bijection f:AB has an inverse f ^-1:BA such that whenever af=b for some a in A and b in B, then bf ^-1=a.

Lemma 1.2: The inverse of a bijection is also a bijection.
Proof: Let f:AB be a bijection, and f ^-1:BA its inverse. Let a be any element in A, and let b=af. Then a=bf ^-1. Therefore f ^-1 is surjective. Again let a be any element of A. There is a unique b in B such that af=b. In other words there is a unique b in B such that bf ^-1=a. Thus f ^-1 is one-to-one.

Note that if f:AB is a bijection, then f uniquely pairs each element of A with an element of B and vice versa. If A and B are finite, they will therefore have the same number of elements.

On nearly all puzzles, moves have inverses. A move can usually be undone, taking you back to the position you had before. For example on the cube, the move R, a clockwise turn of the right face, can be undone by an anti-clockwise turn of the right face. This can be denoted by R^-1, the inverse of R, though R' is more common.

The composition of two functions f:AB and g:BC, is the function that is the result of applying first f and then g. Thus to an element a in A we map the element c in C given by c=(af)g. This function is denoted fg.

Lemma 1.3: If f:AB and g:BC are one-to-one, then fg is also one-to-one.
Proof: Suppose a₁ and a₂ are elements of A, such that a₁(fg)=a₂(fg). Then (a₁f)g=(a₂f)g and since g is one-to-one we must have a₁f=a₂f. Since f is one-to-one, we get a₁=a₂. Therefore fg never maps different elements to the same image element, in other words it is also one-to-one.

Lemma 1.4: If f:AB and g:BC are onto, then fg is also onto.
Proof: Let c be an arbitrary element of C. There must be some element b in B such that bg=c since g is onto. There must be an a in A such that af=b since f is onto. Therefore c=bg=(af)g=a(fg) which means that fg is onto.

Lemma 1.5: If f:AB and g:BC are bijections, then fg is also a bijection.
Proof: Follows directly from previous two lemmas.

Moves can be combined into move sequences. Instead of having to keep track of what each move in a move sequence does to a position, you instead think only of what the sequence as a whole does to it. A move sequence has become a single entity in itself, which is applied to a position.

Any move sequence is a composition of functions. For example, if we apply the move sequence FRB to a position p, we can do the moves one by one, which gives position ((pF)R)B, or we can consider it as a single function FRB, which gives position p(FRB).

The identity function on A is the function i_A:AA defined by ai=a for every a in A. It is easily seen to be a bijection.

Lemma 1.6: If f:AB is a function, then fi_B=i_Af=f.
Proof: For any a in A, we have a(fi_B)=(af)i_B=af=(ai_A)f=a(i_Af). The three functions f, fi_B, and i_Af all have the same effect on any element, they must therefore be the same function.

Lemma 1.7: If f:AB is a bijection, then ff ^-1=i_A and f ^-1f=i_B.
Proof: For any a in A, we have an element b in B such that b=af. Then bf ^-1=a which gives a(ff ^-1)=(af)f ^-1=bf ^-1=a=ai_A. Therefore ff ^-1=i_A. Conversely for any b in B we can find a in A such that bf ^-1=a and then b(f ^-1f)=(bf ^-1)f=af=b. Therefore f ^-1f=i_B.

Note that if two different move sequences always have the same effect on the cube, then they are simply different ways of writing down the same function. Most of the theory developed here is concerned only with the effect, not with how the function is represented by a move sequence.

The identity on the cube is the move sequence that contains no moves at all, or any other move sequence that does nothing such as F2B2L2R2F2B2L2R2.

The move sequences U2D2 R'L FB' and RL'FB'RL'F'B are inverses. You can check this by doing the first and then the second sequence on a solved cube to again find the cube solved. This automatically means that the second sequence followed by the first will also do nothing to the cube.

Lemma 1.8: Composition is associative, i.e. for functions f, g, and h we have f(gh)=(fg)h.
Proof: Let a be any element of the set on which f is defined, then a(f(gh))=(af)(gh))=((af)g)h=(a(fg))h=a((fg)h). Thus f(gh) and (fg)h have the same effect on any element, and are therefore the same function.

Lemma 1.9: (fg)^-1=g^-1f ^-1.
Proof: (fg)(g^-1f ^-1)=((fg)g^-1)f ^-1=(f(gg^-1))f ^-1=(fi)f ^-1=ff ^-1=i.

To undo or invert the move sequence FRB, we must undo the moves starting with the last. The inverse of the function FRB is B^-1R^-1F ^-1, the inverse of move sequence FRB is B'R'F'.

2. Groups and homomorphisms

A group is a set together with an operation usually called multiplication, which satisfies the following conditions:

1. The group is closed under multiplication, i.e. if you multiply together any two elements of the group, this results in another element of the group. The result from multiplication of element g by element h is denoted gh.
2. There is an identity element, i.e. an element e in the group such that for any element g in the group we have ge=eg=g.
3. Every element has an inverse, i.e. if g is an element of the group then there is an element h in the group such that gh=hg=e. The inverse of element g is denoted by g^-1.
4. The multiplication is associative, i.e. if a, b and c are elements of the group, then (ab)c=a(bc).

Lemma 2.1: The identity is unique.
Proof: If e₁ and e₂ are both identity elements, then e₁=e₁e₂=e₂.

Lemma 2.2: Inverses are unique.
Proof: If h₁ and h₂ are both inverses of element g, then h₂=h₂e=h₂(gh₁)=(h₂g)h₁=eh₁=h₁.

Consider the set of all possible move sequences, which are essentially strings of the letters F, L, U, B, R, D. You can combine any two sequences to give a third, simply by concatenating the two strings of letters, and possibly doing some trivial cancellations. Such sequences form a group: There are inverses (simply undo moves, i.e. invert each move and reverse the order), and there is an identity (simply do nothing, i.e. an empty string). Associativity is obvious. Unfortunately there are infinitely many move sequences, so this is an infinite group. Many move sequences have the same effect on the cube. It is therefore much better to consider only the effects of a move sequence. The effects of move sequences on the cube (i.e. the functions used in the first section) also form a group, and this is called the cube group. Thus any two move-sequences that have the same effect on a cube represent the same element of the cube group.

A group is finite if it has a finite number of elements. The number of elements in a group G is called the order of the group, and is denoted by |G|.

There are only finitely many positions of the cube, and therefore only finitely many functions on that set of positions. The cube group is therefore also finite.

There is another group that is interesting, namely the group of rotations of the cube as a whole. We can hold the cube with any one of the six faces at the top, and then have four choices as to which of the adjacent faces should go at the front. There are therefore 24 possible orientations of the cube. A rotation of the whole cube is simply a change between two of such orientations. It is easily seen that these form a group, and there are 24 such rotations. If we also allow reflections, then we get a group of 48 elements, the group of symmetries of the cube.

The order of an element g in a group is the smallest positive integer n for which gⁿ=e (if such an n exists), where the exponent notation gⁿ has the natural meaning of repeated multiplication. If no such number exists, then g is said to have infinite order. The order of g is usually denoted o(g).

In the group of rotations of the cube, there are the following elements:

• 6 rotations of order 4 around axes through opposite centres.
• 3 rotations of order 2 around axes through opposite centres.
• 8 rotations of order 3 around axes through opposite corners.
• 6 rotations of order 2 around axes through opposite edges.
• 1 identity, order 1.

Lemma 2.3: In a finite group G, all the elements have finite order.
Proof: Let g be an element of G. Then g, gg=g², ggg=g³, ... must all be elements of G. As G is finite, we must have eventually have a repetition, i.e. we must have g^k=g^m for some positive integers k>m. Then multiplying by g^-1 we get g^k-1=g^k·g^-1=g^m·g^-1=g^m-1. By repeating this trick m times, this reduces eventually to g^k-m=g^m-m=g⁰=e, which shows that the order of g is (at most) k-m, a finite number.

The cube group is finite, so if you do any move sequence, and continuously repeat it, you will eventually get back the position from which you started.

A subgroup H of a group G is a subset of G that is a group in its own right using the multiplication operation of G.

Lemma 2.4: A non-empty finite subset H of group G is a subgroup if and only if it is closed under multiplication.
Proof: Clearly closed multiplication is a necessary condition to be a group. To show it is sufficient, we must show that the other three group conditions also hold. Let h be an element of H, and n the order of h (which is finite because the proof of lemma 2.3 applies to H as well). Then hⁿ = e must also be an element of H, so H contains the identity element. Also h^n-1·h = h·h^n-1 = hⁿ = e, so the inverse of h is h^n-1 which is also in subgroup H. The multiplication operation is obviously still associative on H since it is associative on the larger set G.

Lemma 2.5: If g is an element of finite order in G, then the set H = {e, g, g², g³, ...} is a subgroup of G, and |H| = o(g).
Proof: The element g has finite order, so clearly H has at most o(g) elements. Let gⁿ and g^m be any two elements of H. Multiplying them together gives g^n+m which is also in H. H is finite and closed under multiplication, so by the previous lemma, it is a subgroup. Suppose H has fewer than o(g) elements. Then gⁿ=g^m for some m<n<o(g), and therefore g^n-m=e with 0<n-m<o(g). This contradicts the definition of o(g), so H must have exactly o(g) elements.

If g is an element of finite order, then the set H={e, g, g², g³, ...} is actually a group, and is called a cyclic group. The element g is its generator and this group is usually denoted by <g>. Note that if g has infinite order, then we explicitly require g^-1, g^-2, ... to be in the set also, so then <g>={..., g^-2, g^-1, e, g, g², g³, ...}.

It is also possible to construct groups from more than one generator. For example if g and h are elements in G, then <g,h> is the smallest subgroup of G that contains g and h. All its elements can be written as a product of g and h (and their inverses), for example gghg^-1hh.

The cube group G_c is generated by the moves, so G_c=<F,L,U,B,R,D>. There are many subgroups of the cube group G_c. Most useful subgroups are formed by elements with some common feature that is not shared by the rest of G_c. Here are some examples:

• The elements that do not move any corners.
• The elements that do not move any edges.
• The elements that only twist corners.
• The elements that only flip edges.
• The elements that do not move anything in the top two layers.
• The elements generated by F and R. Also called the two-generator group.
• The elements generated by F2 and R.
• The elements generated by F, R and U. Also called the three-generator group.
• The elements generated by F2, B2, R2, L2, U2, D2. Also called the square group.
• The elements generated by FB', RL', UD'. Also called the slice group.
• The elements generated by FB, RL, UD. Also called the anti-slice group.

Given a set A, the Symmetric Group S_A is the set of all bijections from A to A, which forms a group under composition (by lemma 2.4). If A is the finite set {1,2,3,...,n}, then its symmetric group is denoted by S_n and the elements of this group are called permutations. This will be dealt with in much more depth later.

If you number the 48 moveable facelets of the cube, the effect of any move sequence is uniquely specified by how it permutes those facelets. This shows that the cube group G_c occurs as a subgroup of S₄₈. This is why the effect of a move sequence is usually also called a permutation.

A homomorphism is a function f:GH between group G and H which respects the group multiplication, so (g₁·g₂)f=(g₁)f·(g₂)f. Note that the first multiplication is in the group G, while the second is in group H.

Lemma 2.6: If f:GH is a homomorphism then e_Gf=e_H and (g^-1)f=(gf)^-1.
Proof: For any g in G, gf=(e_Gg)f=(e_Gf)(gf) so by multiplying both sides by (gf)^-1 on the right gives e_H=e_Gf. For the second part, e_H=e_Gf=(gg^-1)f=(gf)(g^-1f).

The image of a homomorphism is a group, as it inherits all the necessary properties from the group structure of the domain of the homomorphism. If a homomorphism from group G to group H is not surjective, then its image will therefore be a subgroup of H. If a homomorphism is bijective, then it is called an isomorphism and the G and H are called isomorphic groups. Isomorphic groups are in a sense identical - they have the same order and same structure, even though the two groups might occur in a different context.

There is a homomorphism from the normal Rubik's cube to the 2×2×2 cube. Any move sequence on the normal cube can also be performed on the smaller cube. Thus any permutation on the large cube maps to some permutation on the small cube. This mapping is a homomorphism but is not one-to-one, so it shows that the small cube has a group, which is a sense a simplified version of the group of the larger cube. .

The Symmetric Group S_n for some positive integer n is usually considered to be the group of bijections on the set {1,2,3,...,n}. The group of permutations of any finite set of elements A is then isomorphic to the group S_n where n=|A|. This is a really obvious isomorphism - first we label the elements of A as 1 to n in any way by some bijection f:{1,2,..,n}A, and then bijectively map S_n to S_A using that labelling.

Actually, earlier I really should have said that G_c is isomorphic to a subgroup of S₄₈.

Lets extend the multiplication of elements of G to multiplication of sets of elements of G: If K and H are subsets of G, then let KH be the set of all elements kh with k in K and h in H. Note that K and H need not be subgroups, they merely have to lie in some larger group G so that there is a way of multiplying their elements. I introduce this set multiplication because it will simplify proofs later on.

Lemma 2.7: Set multiplication is associative, i.e. A(BC)=(AB)C for subsets A,B,C of a group G.
Proof: Let x be an element of A(BC). Then x=ad for some a in A and d in BC. Also, for d we must have d=bc for some b in B, c in C. Therefore x=a(bc)=(ab)c by associativity of the elementwise multiplication in G. But ab is in AB, and so (ab)c is in (AB)C. Thus A(BC) is a subset of (AB)C. The converse, that (AB)C is a subset of A(BC), is proved in a similar way and the result follows.

Note that we can also multiply a single element x to a set A to get xA, and the result is simply the set of all elements xa with a in A. This is the same as multiplying {x} by A, so associativity still holds.

Lemma 2.8: If g is an element of group G, then gG=G.
Proof: Let h be any element of G. Then h=eh=(gg^-1)h=g(g^-1h) lies in gG. Conversely, any element in gG must be in G since G is closed under multiplication. Therefore G=gG.

3. Actions and orbits

An action of a group G on a set A is a function f:A×GA which satisfies (a,e)f=a for all a in A and also ((a,g)f,h)f=(a,gh)f. What this means is that any element g of the group G will correspond to a function f_g:AA in such a way that f_e is the identity and f_gf_h=f_gh.

Whenever it is clear what group action that we are dealing with, we might as well write ag instead of af_g, as this can make things much more readable. We can do this because the function that assigns f_g to g is a homomorphism, so the group structure is carried through. In particular, g and g^-1 are inverses in the group, and their associated functions on A are also inverse functions. If we have an action of group G on set A we say that G acts on A. Also for elements g in G and a in A we say g acts on a, and gives ag (an element of A).

The orbit of an element a in A is the set containing ag for all g in G. In other words it is the image of a when it is acted on by all the group elements. This set will be denoted aG. Note that the orbit of a will contain a itself since ae=a.

An action is transitive if for any two elements a and b in the set A, there is some g in G such that ag=b. This means that the orbit of any element is the whole set, so aG=A for any a in A.

The cube group G_c obviously acts transitively on the set of positions of the cube, because by definition the positions are those that can be reached by using cube permutations.

Instead lets consider the positions of the cube that can be reached by taking the cube apart and reassembling it. The cube group again acts on this larger set, but this time it is not transitive as there turn out to be 12 different orbits.

Lemma 3.1: Distinct orbits are disjoint.
Proof: Suppose element z lies in xG, the orbit of x. Then z=xg for some g in G. The orbit of z is then zG=(xg)G=x(gG)=xG. Therefore if z lies in two orbits xG and yG, then xG=zG=yG and the orbits are equal. Distinct orbits then cannot have any elements in common.

Let H be the subgroup of G_c with elements that only move the edges but nothing else. Then H acts on the set of all positions. Each orbit is a set containing positions that differ only in their edge arrangement, and therefore all positions in an orbit will have their corners in the same arrangement. Every possible arrangement of corners gives rise to such an orbit containing all the positions that share that corner arrangement. The number of orbits is therefore the number of possible corner arrangements on the cube.

Theorem 3.2 (Cayley): Every group is isomorphic to a subgroup of some symmetric group, in other words every group can be considered a group of permutations on some set.
Proof: Let G act on the set G by right multiplication. By definition of action, each element g in G gives a function f_g:GG (which in this case if defined by the right multiplication xf_g=xg). This function f_g is a bijection on G since it has an inverse, and it therefore lies in S_G, the group of permutations of the set G. The mapping from G to S_G, namely the one that maps g to f_g, is easily seen to be a homomorphism. This mapping is one-to-one because for any g and h in G, if we have f_g=f_h then g=eg=ef_g=ef_h=eh=h. Thus the result follows.

G acts freely on the set A if any element g of G leaving one element a of A fixed must leave the whole of A fixed, i.e. ag=a implies g=e.

Lemma 3.3: If G acts transitively and freely on A, then the set A is in one-to-one correspondence with G.
Proof: Choose any element a in A. Consider the function f:GA which maps g to ag. The image of this function is obviously aG, but as G acts transitively this is the whole of A. Thus f is surjective. Also, if gf=hf then ag=ah, agh^-1=a and since the action is free we must have gh^-1=e and so g=h. This shows that f is one-to-one. Therefore f sets up the correspondence between A and G. Note that the special element a that was chosen will correspond to the identity in G.

It is a neat fact that there is a correspondence between cube positions and cube permutations. Every cube position is reached by some permutation from the solved position, and every (legal) permutation when applied to the solved position gives some cube position. Since a non-trivial permutation will always have a visible effect on any position (i.e. ag is never equal to a), the lemma shows that the positions and permutations are in an exact one-to-one correspondence. This is not necessarily so on other puzzles.

Any puzzle where all the pieces are distinct has a one-to-one correspondence between its positions and its permutations. If some pieces are identical this need not be the case, as it may be so that there is some permutation that when applied to the solved position swaps identical pieces about, which can't be seen. Nevertheless such a permutation might have some effect on other positions, and not be the identity.

We already know how many possible positions the cube has (approx. 43·10¹⁸), and therefore this is the actual size of the cube group as well.

4. Cosets and coset spaces

If H is a subgroup of G (though H can be the whole of G), then H can act on the set G by right multiplication. Any h in H acts on g in G to give gh in G. The orbits of this action are sets of the form gH, are called right cosets. We could instead have used multiplication from the left, to give the orbits Hg which are called left cosets. (Note: some books call gH a left coset and Hg a right coset, especially if defined as a multiplication of H by g rather than as an orbit of a group action.)

Lemma 4.1: Cosets of a finite subgroup H all have the same number of elements.
Proof: H is itself a coset, because H=eH=He. Let gH be some coset. Clearly H has as least as many elements as gH by construction, since any h in H will give an element gh in gH. Conversely, H=eH=(g^-1g)H=g^-1(gH) means that gH has at least as many elements as H by the same argument. Therefore |H|=|gH|. The same arguments show that |H|=|Hg|.

Now we come to an extremely important result.

Theorem 4.2 (Lagrange): If H is a subgroup of finite group G, then |G| is divisible by |H|.
Proof: The (left) cosets of H all have the same size, are disjoint (because they are orbits and distinct orbits are disjoint), and any g in G lies in some coset (namely gH). Therefore G is partitioned into sets of size |H| and so |H| divides |G|.

The number of cosets of H in G is called the index of H in G and is denoted by (G:H). For finite G, Lagrange's theorem says that (G:H)=|G|/|H|.

Lemma 4.3: If g is an element of finite group G, then the o(g) divides |G|.
Proof: The cyclic group <g> is a subgroup of G. Its order is equal to the order of the generator g, so o(g) divides |G| by the theorem.

The size of the cube group is roughly 43·10¹⁸. The exact number has no factor of 13 or 17 for example, so for any move sequence at all, if you repeat it 13 or 17 times on a solved cube it cannot possibly return to the solved position (unless the move sequence itself did not have any effect in the first place).

Corollary 4.4: If g is an element of finite group G, then g^|G|=e.
Proof: g^|G|=(g^o(g))^|G|/o(g)=e^|G|/o(g)=e.

Any move sequence will have no effect if it were repeated 43252003274489856000 times (the order of the cube group), though I would not want to try it.

Corollary 4.5: If |G| is a prime number, then G is cyclic.
Proof: Let g be an element of G. Then o(g) divides |G| so o(g)=1 or o(g)=|G|. If we choose g to be any element that is not the identity then o(g)=|G|. Now the cyclic subgroup <g> has order |G| so it must be the whole group, which means that G is cyclic and generated by g.

If group G acts on A, then the stabilizer of an element a in A is the set of g in G for which ag=a. In other words it is those group elements that keep a stable, not changing it. It is denoted Stab_a.

Lemma 4.6: The stabilizer of a in A is a subgroup of G.
Proof: If g,h are in the stabilizer, then a(gh)=(ag)h=ah=a, so gh also lies in the stabilizer. The stabilizer is thus closed under multiplication. Also ae=a so the stabilizer has the identity. If g is in the stabilizer then ag^-1=(ag)g^-1=a(gg^-1)=ae=a and so g^-1 is also in the stabilizer. Associativity is inherited as usual.

Suppose we have a cube on which all the edges have had their stickers removed so that they are indistinguishable. This puzzle has fewer positions than a normal cube, but has the same group. The cube group acts on this smaller set. The stabilizer of the solved position for example contains all those elements of the group, which move edges only, and these form a group, too.

If H is a subgroup of G, then the left coset space, denoted by H\G, is the set of all left cosets, i.e. its elements are Hx for each x in G. There is a natural group action of G on this set, by right multiplication. In other words, g in G acts on Hx to give the left coset (Hx)g=H(xg). It is easily seen to be a transitive action. Similarly the right coset space is the set of all right cosets and is denoted by G/H.

Lemma 4.7: The stabilizer of Hx in the left coset space is x^-1Hx.
Proof: Clearly (Hx)(x^-1Hx)=H(xx^-1)Hx=HeHx=Hx, so the set x^-1Hx is certainly a subset of the stabilizer. Suppose y lies in the stabilizer, i.e. Hxy=Hx. Then xy lies in Hxy and hence in Hx. Multiplying on the left by x^-1 shows that y is in x^-1Hx.
Corollary: The stabilizer of H in the left coset space H\G is H.
Corollary: For any x in G, x^-1Hx is a subgroup of G

Most solving methods for the cube implicitly work in coset spaces. Let H be the group of permutations of the bottom layer. Suppose you were to remove all the stickers of the bottom layer pieces of a solved cube. Every element in H then looks the same, and so every element in a coset Hx will also look the same. A coset therefore represents all those positions of the normal cube that are treated the same way when the pieces belonging in the bottom layer are ignored. Solving the first two layers is therefore equivalent to working in H\G. You are applying the moves (letting G act on H\G) until all only the last layer remains to be done (i.e. until you reach the coset H). The last layer then solved by working within the group H itself.

Theorem 4.8: Any transitive action of G on a set A, is isomorphic to the action of G on the left coset space H\G where H is the stabilizer of an element a in A.
Proof: Choose any a in A, and let H be its stabilizer. Consider the function f:H\GA defined by (Hx)f=ax for all x in G. This definition is well-defined (not dependent on which x is used to represent the coset) because if Hx=Hy then xy^-1 is in H, axy^-1=a and hence ax=ay. The same argument in reverse shows that if ax=ay, then Hx=Hy, so the function is one-to-one. The action is transitive, so for any b in A we have b=ax for some x in G, in other words the function is onto. This function shows the correspondence between the sets on which the group action occurs, and this respects the structure of the action since H(xy)=(Hx)y and a(xy)=(ax)y.

Corollary 4.9: If group G acts transitively on finite set A, then |A|=(G:Stab_a) where a is any element in A. In particular, if G is finite, then |Stab_a|=|G|/|A|
Proof: The size of a coset space H\G is the number of cosets, which is (G:H) by definition. The mapping in the theorem above shows that any transitive group action is isomorphic to the action of G on the set Stab_a\G for any a in A, and result follows.

Let's consider the group of rotations of the cube, and its action on the 8 corners. There are 3 rotations that keep one particular corner in place (120 degree turn, 240 degree turn, and identity). As there are 8 corners, this immediately shows that the group has size 3·8=24. There are 6 faces that have order 4 rotations, again showing the group has size 24. Similarly the 12 edges with their order 2 rotations.

The Orbit Theorem 4.10: Suppose G is a finite group acting on finite set A. Let c_g be the number of fixed points of g's action, i.e. the number of elements in A such that ag=a. Then the number of orbits of the group action is equal to the sum of the c_g divided by |G|. In other words the number of orbits is equal to the average number of fixed points of the elements g in G.
Proof: Let's count the number of pairs (a,g) with a in A, g in G, for which ag=a. This total is simply the sum of the c_g, but we can count these pairs in a different way. If S is any orbit, then G acts transitively on S. From the previous theorem we know that |Stab_a|=|G|/|S|, so every element a in orbit S contributes |G|/|S| to the sum of fixed points. As there are |S| elements in the orbit S, the total contribution from this and every other orbit is |G|. Hence there are |G|·t pairs, where t is the number of orbits. Therefore t is the sum of the c_g divided by |G|, as required.

This is often known as Burnside's lemma, but has various other names as well. Let's use it to count how many ways the 6 sides of a cube can be coloured if we have n colours to choose from. In our case G is the group of 24 cube rotations. The number of fixed points of each type of rotation (colourings that remain the same under that rotation) is:

• 6 face axis rotations of order 4: n³.
• 3 face axis rotations of order 2: n⁴.
• 8 corner axis rotations of order 3: n².
• 6 edge axis rotations of order 2: n³.
• 1 identity, order 1: n⁶.

This sums to (n⁶+3n⁴+12n³+8n²)/24 = n²(n+1)(n³-n²+4n+8)/24. Substituting n=1,2,3,... gives the answers 1, 10, 57, 240, 800, 2226, etc. If you insist on using 6 different colours, then none of these are fixed by any rotation except for the identity, so there are 6!/24=30 ways to do that (which can also be thought of as 15=5·3·1 ways of choosing opposite colours, 2 mirror image ways of then colouring the cube).

5. Permutations and parity

Every finite group is (isomorphic to) a subset of S_n for some integer n by Cayley's theorem. Now we will now look in more detail at what a permutation does when it acts on the elements of that set A={1,2,3,...,n}. Even though infinite groups are also permutations (on an infinite set), we will assume G is finite from now on.

Suppose g in G acts on some distinct elements a₁, a₂, ..., a_n of A as a permutation in the following way:
    a_ig=a_i+1 for all i<n,
    a_ng=a₁
    ag=a for all other elements a in A
then we call g an n-cycle, and denote it by (a₁ a₂ ... a_n). A cycle rotates a number of elements around in a loop, and does nothing else. In particular, any permutation that just swaps two elements a and b is a 2-cycle denoted (a b), and any permutation that moves exactly three elements will be a 3-cycle. Note that a permutation that moves exactly 4 elements need not be a 4-cycle (a b c d) as it might instead be a product of two 2-cycles such as (a b)(c d) which swaps elements a with b, and c with d.

The pieces of the cube can also move around in cycles, for example the move sequence F2RL'U2LR' is a 3-cycle of edge cubies, namely (FD BU FU).

Lemma 5.1: Every permutation is a product of disjoint cycles.
Proof: Let g be any permutation of set A. Take any a in A that is permuted by g. The elements a, ag, ag² etc. form a cycle because if agⁿ=ag^m then ag^n-m=a. If g does not permute any other elements in A, then g is simply this one cycle. Otherwise we can take an element b of A that does not lie in this cycle and form a new cycle (b bg bg² ...). These cycles are disjoint, because if bgⁿ=ag^m then b=ag^m-n contrary to our choice of b. This process can be repeated to enumerate all the disjoint cycles, and it is obvious that g acts the same on A as the product of these cycles. Therefore g is the product of these disjoint cycles.

For example, the cycle notation for the move F is (FU FR FD FL)(FUR FRD FDL FLU), and similarly any move or move sequence can be written as a product of disjoint cycles to show where each piece moves to. The orientation of the pieces is not quite captured with this notation however. Suppose for example that one piece moves from UFL to URF but that its U facelet ends up in the right face. As we can choose which facelet to mention first (e.g. FUR or RFU or URF all mean the same piece position) we say that UFL moves to RFU, thus specifying its twist at the same time. In the cycle notation for F above it is clear that all the F facelets stay in the F face. It gets a bit trickier if a cycle itself is twisted, for example (UFL RFU FLU FUR LUF URF). Here two corners are swapped, but it is not the same as (UFL RFU) because that would imply that RFU moved to UFL whereas it should move to FLU. We will denote this by (UFL RFU)⁺, so that it is clear that it is a 2-cycle and also that RFU gets an extra clockwise twist when it is moved. Pieces that don't move but become flipped or twisted will be shown as a 1-cycle, e.g. (BRU)^-.

The representation of a permutation as a product of disjoint cycles is essentially unique, as it can only differ in the order of the product, and cyclically permuting each cycle.

Lemma 5.2: Every permutation is a product of 2-cycles, which can all be of the form (1 a). In other words, S_n is generated by the permutations (1 a).
Proof: A cycle (a₁ a₂ ... a_k) can be split as a product (1 a₁) (1 a₂) (1 a₃) ... (1 a_k) (1 a₁). A cycle involving the element 1 can be split into 2-cycles in a similar way. Therefore any product of cycles is also a product of such 2-cycles, and hence any permutation.

If on a puzzle you could swap any two pieces at will, then it is easy to solve any position - with each swap you can put (at least) one piece in its correct position. If each swap you make has to involve the piece at one particular place, then it is still easy.

Lemma 5.3: |S_n| = n! = n·(n-1)·...·2·1.
Proof: An informal proof runs as follows:
Each permutation is a bijection on A. Suppose we were to specify were each element of A is mapped to by a permutation. The element 1 can be mapped to any of the n elements of A. Element 2 cannot be mapped to the same element as 1, so can be mapped to any of the remaining n-1 elements. Similarly 3 is mapped to any one of the remaining n-2 elements, and so on. Clearly there are n·(n-1)·...·2·1. possibilities, each of which specify a unique permutation. Therefore |S_n| = n!.
Here is a more formal proof:
By definition, S_n acts transitively on the set A={1,2,...,n}. From corollary 4.9 we have |Stab_n| = |S_n|/|A|. The group Stab_n consists of all those permutations which keep n fixed, and so Stab_n can be considered as the set of all permutations of {1,2,...,n-1}, and is isomorphic to S_n-1. Therefore |S_n-1| = |Stab_n| = |S_n|/|A| = |S_n|/n. From this, and the fact that |S₁|=1, the result follows from induction.

Any puzzle which has n distinct pieces, and on which any two pieces can be swapped (though this may not be easy!) will have n! permutations and hence n! positions.

The parity of a permutation (odd or even) is the parity of the number of cycles of even length in the disjoint cycle representation, i.e. if the total number of 2-cycles, 4-cycles, 6-cycles etc. is odd, then the permutation is odd, otherwise the permutation is even.

A quarter turn of a face of the cube is a 4-cycle of corners and also a 4-cycle of edges. It is therefore an even permutation.

Lemma 5.4: Multiplying a permutation by a 2-cycle changes its parity.
Proof: If the 2-cycle is disjoint from the other permutation, then it is obvious. Otherwise there are three cases to consider, depending on where the two elements in the 2-cycle lie in the disjoint cycles of the permutation. We can relabel the elements to get one of these cases:
(2 3 4 ... n)(1 2) = (1 2 3 ... n)
(1 2 3 ... a ... n)(1 a) = (1 2 3 ... a-1)(a a+1 ... n)
(1 2 3 ... a)(a+1 ... n)(a a+1) = (1 2 3 ... a-1 a+1 a+2 ... n a )
In all three cases the parity changes (regardless of the parity of n and a) and hence the parity of the whole permutation changes too.

Corollary 5.5: The parity of a permutation is the parity of the number of 2-cycles when written as a product of them.
Proof: Follows from the previous lemma and the fact that the identity is even. Note that a permutation can be written as such a product in many ways of different lengths, but this shows that the parity is fixed.

Parity theorem 5.6: When multiplying permutations, the parities are added. In other words multiplying even by even gives even, odd by odd gives even, and multiplying odd by even gives odd, and even by odd also gives odd.
Proof: Follows immediately from corollary above.

The parity theorem is also sometimes given differently as follows: There exists a homomorphism sgn:S_n{1,-1} that is onto.

Every single move on the cube is an even permutation. Therefore every move sequence is also an even permutation. Thus a single swap of two pieces is an odd permutation and is impossible to achieve using moves alone - you would have to take the cube apart.

The Alternating Group A_n is a subgroup of S_n containing only the even permutations. The parity theorem above proves that it is a group.

Lemma 5.7: Every even permutation is a product of 3-cycles, which can all be of the form (1 2 a).
Proof: Write the permutation as a product of 2-cycles of the form (1 a), which is possible by lemma 5.2. Each pair of 2-cycles is a product of three cycles of the required form because (1 a)(1 b)=(1 a b)=(1 2 a)(1 2 b)²(1 2 a)².

Lemma 5.8: |A_n|=n!/2
Proof: Lets consider the left cosets of A_n in S_n. For any odd permutation p we have p=p(1 2)(1 2) so it lies in the coset A_n(1 2). The even permutations lie in A_n itself, and so there are only two cosets. By Lagrange's theorem we then have |A_n|=|S_n|/2.

Many puzzles have a parity restriction, so that only the even permutations of pieces can be achieved and its group is A_n. This means that such a puzzle will have only half as many positions as it would otherwise have, namely n!/2 instead of n! (assuming its pieces are distinct so that there is a one-to-one correspondence between permutations and positions).

6. Symmetry and Platonic solids

If a three-dimensional geometric shape stays unchanged by a rotation around an axis by an angle less than 360° then that is said to be a rotational symmetry of that shape. In this section we will enumerate all the different types of finite rotational symmetry there can be in a three-dimensional object.

Although this section is not directly related to permutation puzzles, many puzzles are based on three-dimensional symmetry. Also, if you wish to design new three-dimensional permutation puzzles then a familiarity with the possible symmetry types is necessary.

The set of rotational symmetries of a shape clearly form a group: Combining any two rotational symmetries will still leave the geometrical shape unchanged and so is also rotational symmetry. Throughout this section G will denote any finite such group of rotational symmetries. The order of a rotational symmetry is simply its order when considered as an element of this finite group.

Lemma 6.1: For any bounded geometrical shape the axes of the rotational symmetries of the shape (if any) intersect in a single point.
Proof: Take any point of the shape and consider its orbit. This orbit is a set of points that by definition remains unchanged (or rather gets mapped to itself) by any of the rotational symmetries of the shape. Let O be the gravitational centre of these points. This single point will therefore also remain unchanged by any rotational symmetry, and hence must lie on the axis of every rotational symmetry. The result then follows.

Consider a unit sphere centred on the point O from the lemma above. Any axis of a rotational symmetry intersects this sphere at a pair of opposite points, the poles of this symmetry. The order of a pole is the highest number that occurs as the order of one of its symmetries.

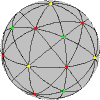The rotational symmetries of the cube have been listed already. These correspond to:

• 6 poles of order 4 (faces)
• 8 poles of order 3 (corners)
• 12 poles of order 2 (edges)

Note that although there are rotational symmetries of order two around the face centres, its poles have order 4.

Lemma 6.2: There is a group action of the group of rotational symmetries G on the set of poles A.
Proof: Let p be any pole in A, and let r in G be any one of its corresponding rotational symmetries. By definition, pr=p. For any rotation s, ps is a pole of the rotational symmetry s^-1rs because (ps)(s^-1rs)=p(ss^-1rs)=prs=ps. Thus ps is a pole for any pole p and any rotational symmetry s, and so this is a group action.

Corollary 6.3: Any orbit of this group action has poles of the same order.

Lemma 6.4: If an orbit S of this group action has poles of order k, then k|S|=|G|.
Proof: G acts transitively on S (by the definition of an orbit), so by Corollary 4.9 we have |Stab_p|=|G|/|S|. The stabilizer of a pole p is the group of the rotational symmetries around this pole. Let r be the rotational symmetry with pole p with the smallest (non-zero) angle, α. If s is any other rotational symmetry around pole p of angle β, then a rotation of β-cα is also a rotational symmetry for any integer c. If we choose c to be the integer nearest to β/α, then -α<β-cα<α. As α is the smallest possible non-zero symmetry angle, we get β-cα=0, and so β must be divisible by α, and hence s is multiple of r. The rotations therefore form a cyclic group generated by r. The order of this group is the order of r, which is also the order of the pole. The result follows.

In the example of the cube there are 24 rotational symmetries, and we do indeed find that multiplying the number of poles of each order by their order we indeed get 24 again: 24=6·4=8·3=12·2.

Lemma 6.5: Let n=|G| and let k_i be the order of the poles in the i-th orbit of the G-action on the set of poles. Then 2(1-1/n)=Sum(1-1/k_i).
Proof: Let t be the number of orbits. From the orbit theorem 4.10 we have t=Sum(c_g)/n. The number of fixed points of any non-trivial rotation g in G is 2. The identity rotation however fixes all poles. From lemma 6.4 we know that there are n/k_i poles in the i-th orbit. Putting this all together we find that t=( 2(n-1) + Sum(n/k_i))/n, where the sum ranges over the orbits from i=1 to t. After some rearranging the result follows. Note that in this rearranging, the t term is split up into t ones and brought into the sum.

Theorem 6.6: The only rotational symmetry groups are:

• The cyclic groups, the symmetry of an n-gonal pyramid.
• The dihedral groups, the symmetry of an n-gonal cylinder.
• The tetrahedral group, the symmetry of a tetrahedron.
• The octahedral group, the symmetry of a cube or octahedron.
• The icosahedral group, the symmetry of a dodecahedron or icosahedron.

Proof: We enumerate all possible solutions of the equation from lemma 6.5.
Suppose there are only two orbits. Then 2(1-1/n)=2-1/k₁-1/k₂ or 2=n/k₁+n/k₂. Both terms on the right must be strictly positive integers (n/k_i is the number of poles in the i-th orbit), so k₁=k₂=n is the only solution. There are only two poles (both of order n), so this means that there is only one axis of rotation, and we get the cyclic group of order n.
Suppose there are three orbits. Then 2(1-1/n)=2-1/k₁-1/k₂-1/k₃, where we can assume that the orbits are arranged so that k₁ is smallest and k₃ largest. Since the left hand side is greater than 1, not all k_i can be 3 or greater. So we can assume that k₁=2. Suppose that also k₂=2. Then k₃=n/2. In this case we have a rotational symmetry of order k around one axis, and k axes of symmetry of order 2. This gives the dihedral group or order 2k.
Suppose now that k₂=3. Then 1/k₃-1/6=2/n, and we find that the only further solutions that occur are (k₃,n)=(3,12), (4,24), or (5,60). These solutions give the symmetries of the Platonic solids. The first solution gives tetrahedral symmetry, and has 8 poles of order 3 (in two orbits of four poles), and 6 poles of order 2. The second solution has octahedral symmetry, with 8 poles of order 3, 6 of order 4, and 12 of order 2. The last is icosahedral symmetry and has 20 poles of order 3, 12 poles of order 5, and 30 of order 2.
No solutions are possible with k₂>3, so there are no more solutions.

The rotational symmetry groups of the Platonic solids - tetrahedron, cube/octahedron, and dodecahedron/icosahedron - are in fact isomorphic to the permutation groups A₄, S₄, and A₅.

Consider the four vertices of a tetrahedron, which are permuted by any rotational symmetry. It is easily seen that the two types of rotation are even permutations of the vertices, and since there are 12 rotations in the group it must in fact be the whole of A₄.

In a similar way every (non-trivial) rotational symmetry of the cube is a (non-trivial) permutation of the four main diagonals of that cube. As there are 24=|S₄| rotations, the group must be the whole of S₄. It is interesting to note that a tetrahedron can be embedded inside a cube so that they share vertices. This also establishes the tetrahedral symmetry group A₄ as a subgroup of the cube's symmetry group S₄. There are actually two ways of embedding a tetrahedron in a cube, and this corresponds to the two cosets of A₄ in S₄.

It is possible to embed five tetrahedra inside a dodecahedron so that all 20 of its vertices are shared. Every (non-trivial) rotational symmetry is a (non-trivial) even permutation of the five tetrahedra, and this shows that the 60 rotations form a group isomorphic to A₅.

The pyraminx is a tetrahedron, and obviously has tetrahedral symmetry. The pieces are moved by rotations of order 3 around the corners, or equivalently rotations of order 3 of the faces. The pyramorphix has the same symmetry, but its moves are around the poles of order 2, i.e. around the edges of the tetrahedron. If moves are restricted to half turns, the tetrahedral shape is maintained.

The Rubik's cube has the octahedral symmetry group, its moves are around the 6 poles of order 4. The Dino cube also has the same symmetry but its moves are around the 8 poles of order 3, and similarly the Helicopter Cube uses moves around the 12 poles of order 2, The octahedral symmetry group (S₄) has the tetrahedral symmetry group (A₄) as a subgroup. This is seen in the pyramorphix - its moves are like the 2x2x2 cube and so in essence have octahedral symmetry, but its shape does not have that symmetry which is why its shape changes when mixed. By restricting to half turns the tetrahedral symmetry is maintained, and so does its shape.

The Megaminx, Impossiball, Alexander's star and the Dogic all have icosahedral symmetry. In fact they all use moves around the 12 poles of order 5. There are some less common puzzles that use the other poles, such as the Starminx I, Bauhinia, Eitan Star (20 poles of order 3) and the Helicopter Dodecahedron (30 poles of order 2).

The Skewb is actually a slightly odd case because the symmetry of its moves is actually tetrahedral as can be seen when taking the puzzle apart - it is impossible to exchange the two sets of corners. The original Skewb (and the Skewb Diamond) has more symmetry than that in its outward shape. A rather pleasing consequence of this is that when the Skewb is embedded into a dodecahedron instead (i.e. the Skewb Ultimate) then the shape does not change because the tetrahedral symmetry group (A₄) is established as a subgroup of the dodecahedral symmetry group (A₅).

Note that it is possible to make puzzles that use moves which are based on several types of poles. For example, it is possible to build a cross between the Dino cube and the 2x2x2 cube, or more easily a Rhombic Dodecahedron (which has octahedral symmetry) where each corner can turn, i.e. both those of order 3 and those of order 4.

7. Conjugation and commutation

If g is an element of the group G, then a conjugate of g is an element h^-1gh for some h in G. Note that if x is a conjugate of y, then y is also a conjugate of x.

Lemma 7.1: Conjugate permutations have the same cycle structure.
Proof: Suppose x and y are conjugates, i.e. there is some g in the group such that x=g^-1yg. Suppose part of the cycle structure of y is (... a b ...), i.e. ay=b. It easily seen that (ag)x=(ag)g^-1yg=ayg=bg. Therefore part of the cycle structure of x is (... ag bg ...). This extends to all elements on which y acts. If y acts on the elements a_i, then x acts on the elements a_ig in the exact same way.

Conjugates have the same cycle structure, so they have the same effect except that it is applied to different pieces. In a puzzle, this means that if you have a move sequence that swaps/cycles/flips/twists some particular pieces, then using conjugates of that move sequence you can swap/cycle/flip/twist any other pieces you want.

Lemma 7.2: If g is any element in G and H is a subgroup, then the g^-1Hg is also a group, and is isomorphic to H.
Proof: The map f:Hg^-1Hg given by hf=g^-1hg is an homomorphism because (h₁h₂)f=g^-1h₁h₂g=g^-1h₁gg^-1h₂g=h₁fh₂f. It is obviously onto. If g^-1h₁g=g^-1h₂g then h₁=h₂ so f is one-to-one. Thus g^-1Hg and H are isomorphic groups.

Consider the group of permutations on the Cube, which do not move the UFL corner. By conjugating this group with the move U, we get permutations that do not move URF. This is clearly isomorphic to the first group, which is obvious if you simply rotate the cube as a whole.

The centre C_G of a group G is the set of elements in G that commute with every element in G, i.e. for any h in C_G and g in G we have gh=hg.

Lemma 7.3: The centre is a subgroup.
Proof: Suppose x and y are in the centre. Then for any g in G, gxy=xgy=xyg so then xy is in the centre. Also ge=g=eg and gx^-1=x^-1xgx^-1=x^-1gxx^-1=x^-1g.

Lemma 7.4: The centre of S_n is trivial (contains only the identity) when n>2.
Proof: Let g be a permutation that is not the identity. Then there must be some distinct elements a and b of {1,2,3,...,n} such that ag=b. Let c be another element that is different to a and b. The permutation (a c)g will map c to b whereas g(a c) maps a to b, so g does not commute with (a c). Therefore g is not in the centre, and hence no non-identity element is in the centre.

Lemma 7.5: The centre of A_n is trivial (contains only the identity) when n>3.
Proof: As above except that the even permutation (a c d) is used instead of (a c).

Many puzzles have a trivial centre group, because usually any move sequence that commutes with everything cannot move any pieces from their position and twists/flips every similar piece the same amount. On the cube it is impossible to twist all the corners in the same direction, which leaves only the superflip, the manoeuvre that flips all 12 edges.

Lemma 7.6: S_n is generated by the two elements p=(234...n) and q=(12).
Proof: p^-1(1 a)p = (1 a+1), so any two-cycle (1 a) can be achieved by conjugation of q by p. By lemma 5.2, these generate all of S_n.

The cube group can obviously be generated by six elements, the six moves that you can do. It can in fact be generated by two elements. Number the corners 1-8 and the edges A-L and let p be the following permutation:
p = (2345678)(BCDEFGHIJKL)
Taking powers of p that are multiples of 7 and 11 we find:
p⁵⁶ = (BCDEFGHIJKL)
p²² = (2345678)
It is fairly easy to show that if q=(12)(AB) then p and q can generate all possible positions of the corners and edges of the cube. To get all orientations as well, we can use q=(12)-(3)+(AB)+(C)+ instead. We find that the positions can still be generated in the same way, but we also have:
q⁴ = (1)+ (2)+ (3)+
q⁶ = (A)+ (B)+
By applying conjugates of these we can generate all orientations of the pieces. Short examples of such generators are:
p = R2FLD'R' = (URF,BDR,LFD,LDB,LBU,LUF,FRD) (FU,DR,FR,UR,DF,BD,RB,DL,BL,UL,FL)
q = UBLUL'U'B' = (UBR,LUF)- (ULB)+ (UR,BU)+ (UL)+
It is even possible generate the cube group using a very different pair p and q, one of order 2, the other of order 4.

If g and h are elements of the group G, then the commutator of g and h is the element g^-1h^-1gh. The commutator is a measure of how much the elements g and h commute - if they do commute then the commutator is the identity. The commutator of g and h is sometimes denoted by [x,y].

Commutators are a very fruitful source of useful move sequences. Since a commutator is a kind of measure of how near two elements commute, taking a commutator of two elements that nearly commute will give something that moves very little and hence is likely to have a useful effect.

Lemma 7.7: Every homomorphism f:GH between groups respects commutators, i.e. [g,h]f=[gf,hf].
Proof: [g,h]f = (g^-1h^-1gh)f = (g^-1f)(h^-1f)(gf)(hf) = (gf)^-1(hf)^-1(gf)(hf) = [gf,hf].

Corollary 7.8: g^-1[x,y]g=[g^-1xg,g^-1yg].
Proof: Taking conjugates is a homomorphism (see lemma 7.2) so the result follows, though it can just as easily be proved directly.

The commutator subgroup of G is the subgroup generated by all commutators in G. Note that the commutator group is not simply the set of commutators itself but instead is generated by that set, as this set is not necessarily closed under multiplication and therefore is not necessarily a group in its own right.

Lets see how far the Cube could be solved by using only commutators. It is fairly straightforward to find commutators that flip two edges, or twist two corners. As conjugates of commutators are still commutators, all the orientations can be solved using only commutators. A three-cycle of edges or corners can also be done by commutation, and so conjugates give every possible three-cycle. By 5.7 every even permutation of edges and every even permutation of corners is possible. Commutators cannot generate odd permutations as it is easily seen that every commutator is even. Therefore the Rubik's Cube can be solved completely using commutators only, except possibly for a single quarter turn.

On the other hand, the Megaminx only has even permutations of the pieces. An argument similar to the above shows that the Megaminx can be solved using only commutators. The same holds for the Dino cube.

8. Normal groups and quotient groups

A subgroup H is a normal subgroup of G if gH=Hg for every element g in G. For normal subgroups, the left and right cosets are exactly the same for each element.

Lemma 8.1: If H is a normal subgroup of group G, then the (right) cosets form a group under the multiplication xH·yH=(xy)H.
Proof: First it must be shown that this definition of coset multiplication is well-defined, in other words that the result (xy)H is independent of which particular elements x and y that are used to represent the cosets. Using the set multiplication we have (xH)(yH)=x(Hy)H=x(yH)H=(xy)(HH)=(xy)H. This is the unambiguous result we want, so the group multiplication of cosets is in fact the set multiplication we were using all along, and it is indeed well-defined. The other requirements of a group are inherited from G as it easily shown that eH is the identity, x^-1H is the inverse of xH, and that multiplication is associative.

If H is a normal subgroup of G then the cosets of H form a group called the quotient group, which is denoted by G/H. The order of the group equals the number of cosets so |G/H|=|G:H|, the index of H in G. If G is finite, this equals |G|/|H|.

The group of permutations that move only corners, but leaves the edge pieces alone, is an example of a normal subgroup on the cube. After solving the edges of the cube first, this group is used when solving the corners.

Lemma 8.2: If H is a normal subgroup of group G, then ghg^-1 is in H for every element h in H and g in G.
Proof: H is normal, so gH=Hg for any g in G. Therefore (gH)g^-1=(Hg)g^-1=H(gg^-1)=H.

Suppose we solve edges first, and then the corners. Suppose also that we have a move sequence that has some useful effect on the corners and which does not move the edges. If we want to use a conjugate of the sequence, in order to apply it to a different set of corners, then we need not worry about the edges at all, because any conjugate will not move the edges.

Lemma 8.3: If H is a subgroup of index 2 of group G, then H is a normal subgroup.
Proof: H has index 2 so there are only two left cosets, one of which is H itself. The other coset therefore must consist of all elements of G that are not in H. The same argument works for right cosets. Let g be any element in G. If g is in H, then gH=H=Hg. If g is not in H, then gH and Hg are both cosets not identical to H. There is only one such coset, so then also gH=Hg, and H is therefore normal.

Corollary 8.4: A_n is a normal subgroup of S_n.
Proof: From lemma 5.8 we know that A_n has index 2 in S_n.

9. Bibliography and Further Reading

There are very many books on Algebra. The two algebra books I mainly used while compiling this page are:

1. P.M. Cohn, Algebra (Vol. 1), second edition, John Wiley and Sons, 1982.
2. I.N. Herstein, Topics in Algebra, second edition, John Wiley and Sons, 1975.

For section 6 I had some help from the following book, which also has a very short section on the Rubik's cube:

3. P. Neumann, G. Stoy, E. Thompson, Groups and Geometry, Oxford University Press, 1994.

There are few books that delve into the mathematics of the Rubik's cube. The following are the groundbreaking classics, and any serious cubist should have at least one of these, if not all:

5. Christoph Bandelow, Inside Rubik's Cube and Beyond, BirkHäuser, 1982.
6. Alexander Frey, David Singmaster, Handbook of Cubik Math, Enslow Publishers, 1982.
7. David Singmaster, Notes on Rubik's 'Magic Cube', Fifth edition, Enslow Publishers, 1980.

This recent book comes highly recommended, and not just because it favourably mentions this site below a quote by Winston Churchill:

8. David Joyner, Adventures in Group Theory, Johns Hopkins University Press, 2002.