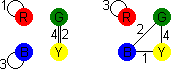Instant Insanity / Buvos Golyok / Drive Ya Crazy
'Instant Insanity' consists of four separate cubes. Each side of a cube
has a single colour. There are four colours. The aim of the puzzle is to put the
cubes on top of one another in a tower such that each side is a mix of all four
colours. The colours of the other faces (hidden inside the tower or top/bottom) do
not matter.
It is often incorrectly thought that each side of the tower should have
only one colour. This is impossible on all versions I have seen.
The second picture shows a Hungarian version (Buvos Golyok) which uses a frame containing balls
with spots on them instead of separate cubes.
The puzzle became popular in the 1960's when it was produced by Parker Brothers,
but it is actually much older. It was first made around 1900 and was then called
'The Great Tantalizer'. More recently it has also been sold as Cube-4, or Trikki 4.
As far as I know, most four cube versions of the puzzle that have been produced
are essentially the same. They nearly all have the following cubes, though possibly
with slightly different colours (for example white instead of yellow, or the yellow,
green and blue colours swapped around), or some of the pieces in mirror image.
This standard version has a unique solution. James East told me about a version
called "Watch It!" which has clocks on the sides of the cubes instead of
colours. Instead of red faces it has clocks showing 2 o'clock, yellow becomes 4
o'clock, green is 8 o'clock, and blue is 10 o'clock. The aim of this puzzle is
for the sides to add up to 24 hours. This can be solved by having each side
show all different clocks, since 10+8+4+2=24. It does however have ten more
solutions, since the 24 can also be reached by 10+10+2+2 or 8+8+4+4.
I recently acquired a German version called Mutando, made by Logika
Spiele,which has a different arrangement
of colours. It not only allows the usual arrangement with four colours on each side, it
is also possible to form a 2×2×1 block with each face one colour. Its
cubes have the following colours:
There is also a nice version with 6 cubes and 6 colours called Drive Ya Crazy. It is available
from Uwe Meffert. Note that all six colours (yellow, orange,
red, green, blue, cyan) occur on each cube. Its cubes have the following colour arrangement:
A nice five cube version called Dorobo is by the Japanese manufacturer Hanayama.
Its cubes have the following colour arrangement:
The number of positions:
The cubes can be stacked in any order, each cube has 24 orientations, giving a
maximum of 4!·244 positions. This limit is not reached because:
- The solved puzzle as a whole has 8 orientations (8)
- The order of the cubes does not really matter to the solution (4!)
This leaves only 244/8 = 41,472 distinct positions.
Similarly six cubes have 246/8 = 23,887,872 positions.
If your browser supports JavaScript, then you can click on the link below.
This script allows you to colour in your own four cubes and find all their
solutions.
Solution:
Here is the unique solution to the standard version described above. As mentioned
earlier, the cubes can be in any order. The cube with three red faces is
easiest to recognize, so start with that one. The other cubes can also be
recognised by the colours which occur more than once.
| Instant Insanity |
Mutando |
Drive Ya Crazy |
|---|
|
|
|
|
There is a neat method for solving this puzzle. It shows whether
there is no other solution, and works for any version of the puzzle.
- Number the cubes. I will use the numbering shown at the top of the page.
- You will next build a graph. Draw four points, arranged in a square
which will represent the four colours.
- Take the first cube. There are three pairs of opposite faces. For
each pair, draw a line between the points of those two colours,
and mark it with the number 1 to show it comes from the first
cube. Note that if two opposite faces have the same colour, then
you will draw a loop from the point of that colour back to itself.
- Repeat this for the other three cubes, but now marking the lines with
the appropriate numbers 2,3 and 4.
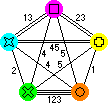
- With the standard version this results in the following graph:
- Now find two loops in this graph, such that each loop visits all four
colours once, and uses lines with each number once. The two
loops may not use the same lines.
-
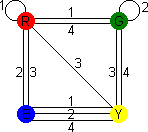
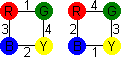 In this example, you can find the loops:
In this example, you can find the loops:
R - 1 - G - 4 - Y - 2 - B - 3 - R
R - 4 - G - 3 - Y - 1 - B - 2 - R
One loop will solve the front and back, the other the right and left sides.
- Take cube 1, and see where it occurs in the loops. Cube 1 connects R-G and Y-B,
so place the cube with Red at the front (Green at the back) and Yellow on
the right (Blue on the left).
- Do exactly the same for the other cubes, and you will then have a solution when
they are stacked together. This solution is unique up to reordering the cubes or turning over the stack
of cubes.
Actually, it might be possible (or necessary) to solve a set
of opposite sides with several loops instead of one. In the example we needed a 4-cycle for
each set of opposite sides, but two 2-cycles, or a 3-cycle with a single loop can work just
as well. Together they will still have to use all 4 colours and all four cubes. The
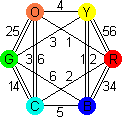
solution to Mutando is such a solution. Its graph is as follows:
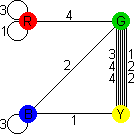
As red is only connected to one other colour, it is clear that there is no loop
that contains red and other colours. The solution is this:
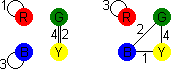
R - 1 - R, B - 3 - B, G - 4 - Y - 2 - G
R - 3 - R, B - 2 - G - 4 - Y - 1 - B.
Again this solution is essentially unique, though most cubes have two orientations
that show the same colour. This puzzle is actually much easier than the standard
instant insanity.
Mutando also allows you to make a 2×2×1 block,
where each side has a single colour. As you can see from its graph, each cube has green
opposite yellow, so the 2×2 sides must be green and yellow. Cube 3 will have red
and blue on its other visible sides. Cube 1 also must show red, cube 2 has no red, so
there is exactly one 2×1 red side formed by cubes 3 and 1. Cube 4 has no blue, so
cube 2 must form the blue side with cube 3. The red side of cube 4 must be hidden, so the
other sides can only be yellow and green. To recap:

| Side | Colour |
|---|
| Front | Blue |
| Left | Red |
| Back | Yellow |
| Right | Green |
|
| Cube | Position |
|---|
| 1 | Back left |
| 2 | Front right |
| 3 | Front left |
| 4 | Back right |
|
Note that there are actually two solutions. The top can be yellow, the bottom green
or vice versa.
Drive Ya Crazy has six cubes, but the same method can be used
to analyse the solutions. Draw six points in a hexagon to represent the six colours, and
as before connect each pair of opposite faces on each cube. This results in the following
graph:
This graph is a bit more complicated than the others, but it turns out to have the
nice feature that there are three sets of loops that visit each colour using all cubes:
O - 1 - R - 2 - C - 5 - B - 6 - G - 3 - Y - 4 - O
O - 2 - G - 4 - C - 6 - O, Y - 1 - B - 3 - R - 5 - Y
O - 5 - G - 1 - C - 3 - O, Y - 2 - B - 4 - R - 6 - Y
Any two of these sets gives a solution. Note that you may reverse the direction
of one or more of the loops and this may result in a slightly different solution. An
interesting feature of this puzzle is that if you have a solution (such as the one
shown at the beginning of this section) then it does not matter which direction you stack
the cubes in, i.e. you can put them in a row on top of, next to, or behind each other, giving
a solution each way. These three solutions correspond to the three ways of choosing two of
the three sets of loops above. If you choose the two pairs of short loops for the four
sides then the long loop is used in the internal cube faces, and this allows the cubes to
be reordered such that touching faces have the same colour.
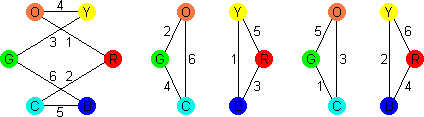
The Dorobo five cube version also is easily analysed by the same method. It has the following graph:
The diagonals all belong to cubes 4 and 5, and the outer edged to the other three
cubes. Therefore the loops we are looking for must use exactly two diagonals. There
is only one loop shape that does so, which makes it easy to find the solution. Like
the Drive Ya Crazy version this graph splits into three loops that visit each colour using all cubes:
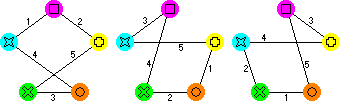
G - 3 - O - 4 - C - 1 - P - 2 - Y - 5 - G
G - 2 - O - 1 - Y - 5 - C - 3 - P - 4 - G
G - 1 - O - 5 - P - 3 - Y - 4 - C - 2 - G
There are essentially three solutions, constructed as before by using any two
of these loops to determine the two pairs of opposing sides. Unlike the Drive Ya Crazy,
it is not possible to use the third loop to make the touching faces the same because
some cubes would need to be turned over to get the matching faces together. This also
means that to go from one solution to the other you must not only just stack them in a
different direction but also turn around two cubes (cubes 2 and 5 to be exact).








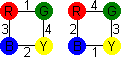 In this example, you can find the loops:
In this example, you can find the loops: