Notation:

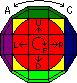
In the solution below you will always hold the puzzle so that one of the faces is towards you, with the bands of tiles running through it horizontally and vertically. Moving the horizontal band of tiles to the right or left for one tile will be denoted with the letters R or L respectively. Similarly moving the vertical band of tiles up or down is denoted by U or D, shifting the third band of tiles clockwise or anti-clockwise is denoted by C or A and turning the front face clockwise one quarter turn is denoted by F. A move letter can be followed by a number indicating how often the move is performed (thus F2 is a half turn of the front face, and L3 means shifting the horizontal band 3 tiles to the left etc.).

Solution:

1. To move a tile from the front centre to the top centre, do:
   D F D F U2.
2. To move a tile from the front top to the top centre, do:
   F D2 F3 U2.
3. To move a tile from the front top to the top front, do:
   1. Without twisting: F D F3 U.
   2. With clockwise twist: D F U F D F3 U.
   3. With half turn: D F2 U F D F3 U.
   4. With anti-clockwise twist: D F3 U F D F3 U.
4. To move a tile from the front centre to the top front, do:
   1. Without twisting: F2 D F2 U.
   2. With clockwise twist: F3 D F2 U.
   3. With half turn: D F2 U.
   4. With anti-clockwise twist: F D F2 U.

The sequences above are more than enough to solve 5 faces.

Phase 2: Orient the pieces of final face.
Hold the final face at the front.

1. First you must determine what the correct orientation of the pieces is. Of the 4 possible orientations of the front face, only one can be solved. The way to determine the correct orientation, is to count how many clockwise quarter turns of the individual tiles you would need to get all the numbers on them upright. This should be a multiple of 4 for it to be solvable. If it is not, then give the front face as many clockwise quarter turns as needed that would make this number a multiple of 4.
2. Choose one of the tiles that need to be twisted. If it does not lie in the horizontal band of tiles (i.e. it is at the front top or bottom), then do F.
3. Do C3, then R until the piece is in the centre of the right face, and then do A3.
4. Turn the top face as much as necessary to give the tile the twist it needed.
5. Do C3, then L until the horizontal band is back into position, and then do A3.
6. The steps b-e above have twisted the tile correctly, and also twisted the top centre tile in the opposite direction. Repeat steps b-e for all tiles that need to be twisted. Afterwards, the top centre tile should be correct again provided you chose the correct face orientation in step a.

Phase 3: Fix permutation parity.
Note that you could actually do this parity fix as soon as you have determined the orientation of the pieces, i.e. after step 2a.

1. Determine the parity of the permutation of the tiles of the final face. If you don't know what that is or find it hard to determine, you can ignore this phase for now and come back to it if the next phase fails to solve the puzzle.
2. If the tile permutation is odd (i.e. if you would need to swap pairs of tiles an odd number of times to solve it), then do the following sequence of moves:
   R2 RURD RURD RURD R5
   This does a 4-cycle of pieces, one from each side face, without affecting any other pieces.
3. Go back to phase1 to fix the four pieces that were disturbed. When you next reach this point the permutation parity on the last face will be even.

Phase 4: Position the pieces of the final face.

1. The following sequence of moves performs a 3-cycle of pieces in the front face. The right tile moves to the bottom, the bottom tile to the centre, and the centre tile to the right.
   DLUR F DLUR F DLUR F2
   To cycle the three tiles the other way, do the inverse of the sequence:
   F2 LDRU F3 LDRU F3 LDRU
2. It is fairly easy to use the sequences above to solve the final face. You need to perform the sequence at most three times. The first 3-cycle can always solve at least one of the 4 non-central tiles, the next will solve one of the adjacent ones, and the last will solve the final three tiles.
3. Once three tiles are in position, then the last two should also automatically be solved. If not, then you have done the permutation parity fix in phase 3 incorrectly, so go back and do the parity fix move sequence and try again.
    
4. An alternative method is often slightly quicker. The sequence ULDR does exactly the same 3-cycle of pieces as above, but also does the same on the back face. Using this together with turns of the front face, the front face can be easily solved as before provided you take care to keep the puzzle in the same orientation all the time. Once the front face is solved, the back face might have been disturbed but it can be solved using the 3-cycle in part a.