Izzi is a tiling puzzle consisting of 64 square cardboard tiles designed by Frank Nichols and made in 1992 by Binary Arts (now called ThinkFun). A square can be divided into 8 equal triangles by its diagonals and the horizontal and vertical mid-lines. There are 70 (see below) possible patterns created by colouring the triangles either black or white, and 64 of those patterns are used on the tiles in the Izzi puzzle. The six patterns not used are shown below.

The aim of the puzzle is to put the tiles in an 8×8 square, obviously while making sure that all the touching tile edges match in colour. The packaging shows one solution, reproduced below:

As there are very many solutions ("Zillions" apparently), extra conditions can be imposed such as a diagonal line across the large square as shown here:

Diagonal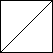

Other solvable patterns shown on the packaging are:

Diamond	X	Border

In fact, it is possible to do the patterns above such that the left side of the large square matches the right side, and the top side the lower side. Six further patterns I have found solutions to (with matching sides) are:

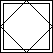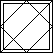Diagonals	Diamond and diagonal	Diamond and border	Cross and border	Diagonals and border	Diamond, diagonal, and border

Note that given one solution, others can be found by taking the mirror image, and/or exchanging white and black.

The number of tiles:

As it is not easy to say anything useful about the number of positions, I will instead show how Burnside's Lemma can be used to quickly count that there are only 70 Izzi tiles possible.
First of all, there are 8 triangular parts on a tile which can each be black or white, giving 2⁸=256 tiles.
Next we count how many have 180 degree rotational symmetry. If we colour half a tile, the other half is then determined by the symmetry, so there are 2⁴=16 tiles with that symmetry.
Finally, we count the tiles with ±90 degree symmetry. Here a quarter of the tile determines the rest, giving 2²=4 such tiles.
Now we can apply Burnside's Lemma using the numbers are 256, 16, 4, and 4. Note that the 4 is repeated, once for clockwise quarter turns, and once for anti-clockwise turns. The average is (256+16+4+4)/4=70, so there are 70 possible tiles.