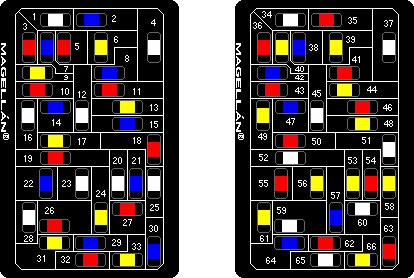
The Magellán puzzle has a rectangular casing with a drawing of 33 numbered regions on both sides. The regions on the front are numbered 1 to 33, on the back 34 to 66. Each region contains a small coloured wheel which can be turned to make any of its six colours visible. The wheels turn independently, though some of the wheels are visible on both sides of the puzzle so that setting the colour of the front region determines the colour of the corresponding back region. The aim is to set the wheels such that no two adjacent regions have the same colour. This is quite easy to do with the 6 colours that are available, but is harder if you want to use fewer.
A drawing of the puzzle showing all the regions is shown below. Note that the two sides are the same except for the numbering.
The wheels all have the same six colours but not all in the same order. The order of the colours around a wheel does not matter for wheels that are only visible on one side, but wheels visible on both sides of the puzzle will obviously only show colours that lie opposite each other on the wheel. The wheels come in two versions. The wheels that are visible on both sides are:
| Order of the colours | Wheels visible on both sides |
| White, Blue, Green, Black, Red, Yellow | 2/35, 14/46, 21/55, 22/54, 29/62 |
| Green, White, Blue, Black, Red, Yellow | 3/37, 4/36, 13/47, 32/65 |
Magellan comes in 3 different versions. Mine has a completely black casing, but there are also ones that are completely white, and others half black half white.
There is a well-known theorem in mathematics called the Four Colour Theorem. It states that with just four colours it is possible to colour the countries on any flat map such that adjacent countries get different colours. Some maps can be done with fewer colours, but four colours is always enough for flat maps for which each country consists of only one region. This theorem shows that it is possible to solve either side of the Magellan with 4 colours, but it says nothing about solving both sides of the puzzle simultaneously, as the colouring on one side influences that of the other.
There are 58 wheels, and each can show any of the 6 colours. This gives a 658 positions. As with most pattern matching puzzles this number is not a good measure of its difficulty.
The graph below repressents the map of the Magellan. A line between two numbers means that the regions with those numbers are adjacent, and so must have different colours.
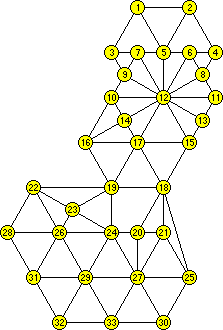
Suppose we try to use only three colours. After colouring region 27, its
neighbours must then use the two remaining colours. These neighbours form a loop,
so they must alternate between the two colours. Unfortunately there are seven regions
in that loop, an odd number, so they cannot alternate throughout and the fourth
colour has to be used.
Another interesting fact is that region 12 has a large number of neighbours, eleven
of them. It is therefore easiest to choose the colour of region 12 first (and similarly
region 45 on the other side), and then do the rest. The puzzle then becomes relatively
simple to solve systematically.
Below is a solution of the puzzle using only 4 colours.