Jaap's Puzzle Page

Marusenko Sphere

Marusenko Sphere Prototype Marusenko Sphere, two colour

The Marusenko Sphere is a ball-shaped puzzle which is an extension of the 2×2×2 puzzle balls. The ball is divided into eight octants by three perpendicular cuts and moves just like a 2×2×2 Rubik's Cube. Unlike such puzzle balls, this puzzle also has 24 pieces arranged in 6 circular faces. Each octant has three such pieces, in three different faces.

This puzzle was invented by Alexandr Marusenko, and has the patent WO2007/028837, published on 15 March 2007. The pictures above show a prototype version, which has painted colours, and a two-colour production version.

The number of positions:

The 8 octant pieces have 3 orientations each, giving a maximum of 8!·38 positions. There are also 24 face segments which can be arranged in 24! ways, resulting in a total of 24!·8!·38. Just as with a 2·2·2 cube, this limit is not reached because:

This leaves 24!·8!·37/24 = 2,279,626,699,712,199,018,518,937,600,000 or approximately 2.2·1030 positions.
That number is based on the assumption that all pieces are distinct and that orientations of the octant pieces are distinguishable. This is not the case on most colour schemes.

There are 5 types of colour scheme available, labelled with difficulty levels 1 to 5. The lower levels have more identical pieces, and so fewer possible positions. To get the exact number of distinct positions you then have to take into account that some positions have symmetry by applying Burnside's Lemma.
Level Picture Name Octants Segments Approximate Exact
1 Level 1 Black and White 4+4 12+12 8!·24! / (24·4!2·12!2) 7,889,304
2 Level 2 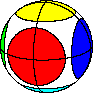Circular 8 4+4+4+4+4+4 8!·24! / (24·8!·4!6) 135,277,941,853,080
3 Level 3 Flag 4+4 4+8+8+4 8!·24! / (24·4!4·8!2) 1,932,542,454,240
4 Level 4 Classic 2+2+2+2 6+6+6+6 8!·24! / (24·2!4·6!4) 242,418,070,100,640
5 Level 5 Triangular 1+1+1+1+1+1+1+1 3+3+3+3+3+3+3+3 8!·24! / (24·3!8) 620,590,250,933,452,800,000

Links to other useful pages:

marusenko.com is the homepage of this puzzle.

Notation:

Let's use the same notation as with a 2·2·2 cube. A clockwise quarter turn of half the ball is denoted by one of the letters L, R, F, B, U and D for each side of the puzzle (Left, Right, Front, Back, Up, and Down). Anti-clockwise quarter turns are denoted by the letter followed by an apostrophe (i.e. L', R', F', B', U' or D'). Half turns are denoted by the letter followed by a 2 (i.e. L2, R2, F2, B2, U2 or D2). Turns of the small circular faces are denoted in the same way, but with small letters, i.e. l, r, f, b, u, d.

Solution to Level 5:

Phase 1: Solve the segment pieces.
In this phase the segment pieces are arranged such that each octant piece has its three matching segment pieces. This reduces the puzzle to the 2×2×2 ball.

u F'D'F u2 R'D2R u2
u F' D' F
u2 R' D2 R
u2

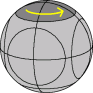
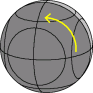
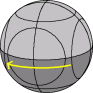
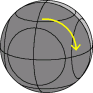
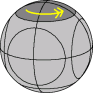
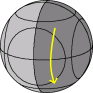
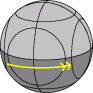
There is a sequence of moves that swaps two segment pieces without changing any other part of the puzzle. You can use this sequence to solve all the segment pieces one by one. There is a much faster way, similar to the method described on the Dogic, which I will not describe here.

  1. Find two segment pieces you want to swap. They must lie in different octant pieces. If at all possible, they should be chosen such that the swap would make at least one of the two pieces match up to an octant piece.
  2. Hold the puzzle so that one of the two segments you want to swap lies in the top circle (the u face), at the back right.
  3. Using only turns of the F, L, D ball halves, put the other segment also in the top circle, at the front right, next to the first segment.
  4. Do the move sequence: u F'D'F u2 R'D2R u2
    This should swap the two segments. This sequence does rearrange the octants as well, but you can follow it with R'D2R F'DF to have no changes other than the segment swap.
  5. Repeat steps a-d until all segment pieces are correct relative to the octant pieces.

Phase 2:Solve the octants.
The puzzle can now be solved in the same way as a 2×2×2 Rubik's Cube.