Jaap's Puzzle Page

Megaminx

Megaminx Megaminx with tiles Supernova Ball.B, flags design Holey Megaminx

This is a variant of the Rubik's cube, in the shape of a dodecahedron. It is a very logical progression from the cube to the dodecahedron, as can be seen from the fact that the mechanism is virtually the same, and that many people invented it simultaneously. To quote from Cubic Circular, Issue 3&4, (David Singmaster, Spring&Summer 1982):

"The Magic Dodecahedron has been contemplated for some time. So far I have seen photos or models from: Ben Halpern (USA), Boris Horvat (Yugoslavia), Barry Lockwood (UK) and Miklós Kristóf (Hungary), while Kersten Meier (Germany) sent plans in early 1981. I have heard that Christoph Bandelow and Doctor Moll (Germany) have patents and that Mario Ouellette and Luc Robillard (Canada) have both found mechanisms. The Hungarian version is notable as being in production ... and as having planes closer to the centre so each face has a star pattern."
"Uwe Mèffert has bought the Halpern and Meier rights, which were both filed on the same day about a month before Kristóf. However there is an unresolved dispute over the extent of overlap in designs."

There are several versions that have been made.
The standard megaminx has either 6 colours or 12 colours. The face layers are fairly thin, so the edge pieces have some width to them.
A version called the Supernova was made in Hungary, and it has 12 colours and thicker face layers which meet exactly at the middle of an edge.
The Ball.B is a spherical of this puzzle. The version with flags on the faces has the extra complication that the orientation of the centres are visible, making it more difficult.
The Holey Megaminx is a version without face centres, inspired by the Void Cube.

Related puzzles are Alexander's Star, which is equivalent to a megaminx without corners or centres, and the Impossiball, which is equivalent to a megaminx without edges or centres.

The number of positions:

There are 30 edge pieces with 2 orientations each, and 20 corner pieces with 3 orientations, giving a maximum of 30!·20!·230·320 positions. This limit is not reached because:

This leaves 30!·20!·227·319 = 100,669,616,553,523,347,122,516,032,313,645,505,168,688,116,411,019,768,627,200,000,000,000 or 1.0·1068 positions.

If only 6 colours are used, giving 15 pairs of indistinguishable pieces, then this number has to be divided by 214 (not 215 since only an even number of swaps are possible) which gives 6,144,385,775,971,883,979,645,753,925,393,402,415,081,061,792,664,780,800,000,000,000 or 6.1·1063 positions. Despite these huge numbers, the puzzle is no harder than the Rubik's cube.

If the face centres have visible orientations, then the number of positions is multiplied by a factor 512 because each of the 12 centres can be twisted independently. A super-megaminx with 12 colours therefore has 30!·20!·227·319·512 = 24,577,543,103,887,535,918,583,015,701,573,609,660,324,247,170,659,123,200,000,000,000,000,000,000,000 or about 2.5·1076 positions.

Links to other useful pages:

Meffert's puzzles Uwe Meffert's pages. He produces and sells many puzzles, including a stickered megaminx with 6 colours. He used to sell tiled ones with 12 colours too.
Meffert's pages The solution as provided in its booklet.
Mark Longridge's page Some move sequences, and some nice spot patterns.
David Joyner's Page A proof by one of his students, formalizing the permutation group of the puzzle and proving the assertions I used above to calculate its size.
David Joyner's Page A catalogue of moves that can be used to solve the puzzle.
Grant Tregay's Page speedsolving solution.
Andy Klise's Guide to the Megaminx last layer.

Notation:

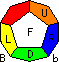Let U, R, F be three adjacent faces (Up, Right and Front), in other words, U, R, F are faces arranged clockwise around a vertex. Let D be the other face adjacent to both F and R. Clockwise 1/5 twists of a face are denoted by the appropriate letter, anti-clockwise 1/5 twists by U', R', F' or D'. In the solution below, the D face is usually still unsolved. We can denote the locations of the edge pieces by using two letters, for example UF is the edge location that lies in both the U and F faces. Similarly, corner locations are denoted by three letters as they lie in three faces.

Solution:

If you can solve the top and middle layer of the Rubik's cube, then you can use the same techniques on the megaminx to solve everything but the final layer.

Phase 1: Solve all but final face

  1. Solve the edge pieces of one face. This is easy to do and need not be explained in detail. Let that face be the U face.
  2. Solve the corners of the U face as follows:
    1. Find a corner that belongs on the U face.
    2. Hold the puzzle so that the corner belongs at URF, and that face D is unsolved.
    3. Use any turns that do not disturb already solved pieces to place the corner at RDF.
    4. Use one of the following sequences to place the corner:
    RDF->URF: R'D'R
    FRD->URF: FDF'
    DFR->URF: R'DR FD'D'F'
    These sequences only disturb the FR edge piece and the D layer, but nothing else except for the corner. The sequences differ only in the orientation of the corner. If you use the wrong sequence for your situation, the URF corner can be twisted in place by R'DR FDF'.
    5. Repeat 1-4 till done. If necessary you can use to use this method to displace a corner that you need somewhere else.
  3. Place all yet unsolved edges adjacent to the solved corners. This is similar to placing the corners, except that you use the following sequences to place them:
    DR->FR: DFD'F' D' R'DR
    FD->FR: D'R'DR D FD'F'
    These sequences only disturb the D layer, but nothing else except for the edge. If an edge is in position but flipped, then displace it by placing any other edge piece there with one of the sequences, and then insert the edge piece in the correct orientation.
  4. Repeat steps b-c to solve each adjacent face in turn, until only one unsolved face is left.

In the phases below, we need to have names for all the faces adjacent to the D face in order to describe all the possible pieces on the D face. Lets call these faces in clockwise order: L, F, R, b, B.

Phase 2: Orient the edges of the final face.
The edges are flipped in pairs. It is impossible to have only one edge upside down.

  1. Hold the puzzle so that the unsolved face is D, one edge to be flipped is at DR, and another is either at DL or DF.
  2. Do one of the following sequences to flips the edges:
    To flip DF, DR, do R D F D' F' R'
    To flip DL, DR, do R F D F' D' R'
  3. Repeat the above if necessary.

Phase 3: Position the edges of the final face.

  1. Rotate D to place as many edges as possible in their correct places. If, like Alexander's Star, your megaminx has only 6 colours, you might find that the edges are in an odd permutation. In this case you will have to swap any two identical edges elsewhere on the puzzle and try solving it again.
  2. Hold the puzzle so that you can use one of the following sequences to solve it:
    1. DR->DF->DL->DR: R D R' D R D'D' R'
    2. DR->DL->DF->DR: R DD R' D' R D' R'
    3. DR->DF->DB->DR: R D R' DD R DD R'
    4. DR->DB->DF->DR: R D'D' R' D'D' R D' R'
    5. DR-DB, DF-DL: R D R' D R D' R' DD R DD R'

Phase 4: Position the final corners.

  1. Hold the puzzle so that you can use one of the following sequences to solve it:
    1. DFR->DLF->DBL->DFR: RUR' D RU'R' D RUR' D'D'RU'R'
    2. DFR->DBL->DLF->DFR: RUR' DD RU'R' D' RUR' D' RU'R'
    3. DFR->DLF->DbB->DFR: RUR' D RU'R' DD RUR' DD RU'R'
    4. DFR->DbB->DLF->DFR: RUR' D'D'RU'R' D'D'RUR' D' RU'R'
    5. DFR-DbB, DLF-DBL: RUR' D RU'R' D RUR' D' RU'R' DD RUR' DD RU'R'
    Note the similarity between these sequences and those of phase 3.

Phase 5: Orient the final corners.

  1. Hold the puzzle so that the DFR corner needs to be twisted anti-clockwise. If there is no such corner, then put a different twisted corner there.
  2. To turn DFR anti-clockwise, and another clockwise, do one of these:
    1. DFR->RDF, DLF->LFD: RU'R'F'U'F D F'UFRUR' D'
    2. DFR->RDF, DBL->BLD: RU'R'F'U'F DD F'UFRUR' D'D'
    3. DFR->RDF, DbB->bBD: RU'R'F'U'F D'D' F'UFRUR' DD
    4. DFR->RDF, DRb->RbD: RU'R'F'U'F D' F'UFRUR' D
  3. Repeat the above until all corners are correct.

Phase 6: Orient the centres (for some types of megaminx only).

  1. Hold the puzzle so that the D face has a centre that needs to be twisted.
  2. The following sequences twist the centre by the amounts listed:
    1. Once clockwise: F'F' RR FF D R'R' D performed three times
    2. Once anti-clockwise: RR F'F' R'R' D' FF D' performed three times
    3. Two steps clockwise: R' DD R D R' DD R F' DD F D F' DD F DD
    4. Two steps anti-clockwise: F' D'D' F D' F' D'D' F R' D'D' R D' R' D'D' R D'D'
  3. Repeat the above until all centres are correct.