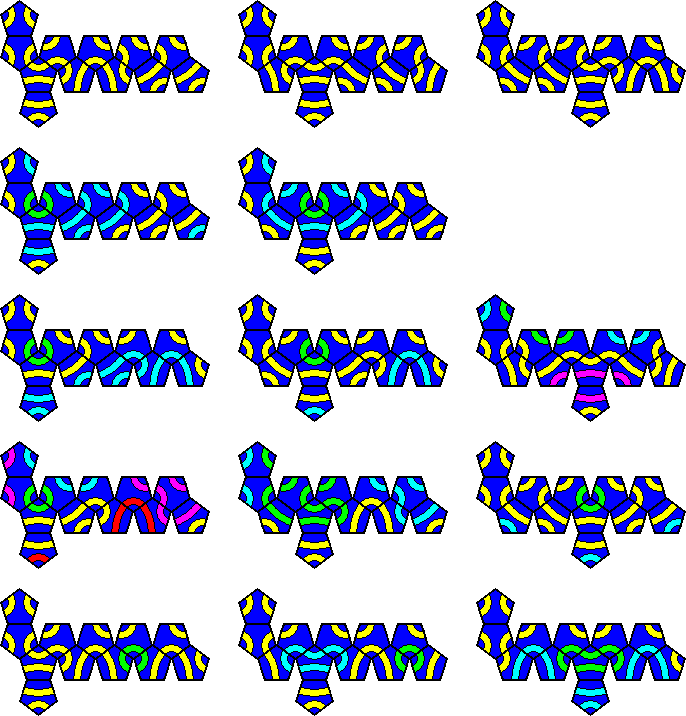The Möbius Line Puzzle is dodecahedron with pentagonal tiles attached to each face.
The tiles can rotate but cannot be removed. There are two line segments on each tile
and the aim of the puzzle is to rotate the tiles such that all the line segments connect
up and form one long loop over the surface of the dodecahedron. There is a blue and a red
version of this puzzle, but apart from colour they are identical.
There are two types of tile, shown on the right. There are the only arrangements of line segments where they do not cross. Each type of tile is used on one 'hemisphere' of the dodecahedron, i.e. on one face and the five neighbouring faces surrounding it.
This puzzle can easily be analysed by hand without the help of a computer. Find a tile that is surrounded by tiles of the same type. There are two of these, at opposite sides of the puzzle like North and South poles. There are five ways these two can be oriented with respect to each other. Every tile has exactly one edge without a line crossing it. This means that in any solution the tiles fall into pairs that share an uncrossed edge. The chosen orientation for the poles therefore fixes the orientation of two more tiles, and the remaining eight tiles need to be divided into four pairs of adjacent tiles. It turns out that in all five pole tile orientations, there are five ways to pair up the remaining tiles. This gives merely 25 loop patterns. Three of these are symmetric, so by discounting mirror images there are really only 14 patterns.
Below all 14 patterns are shown. The top row are the real solutions with a single loop. One pattern has five loops, one has four loops, one has two loops, and the remaining eight patterns have three loops.
