Octacube

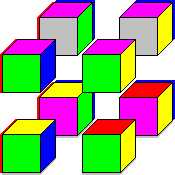
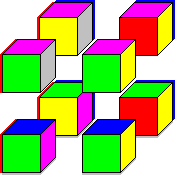
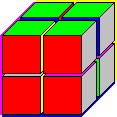
Octacube, as the name implies, consists of eight cubes. The eight cubes all have the same 6 colours on their faces, though they are all arranged differently. The aim is to build a 2×2×2 cube, so that every side of the larger cube has only one colour, and so that faces that touch each other match in colour.

There are two versions of this puzzle. The version pictured above has metallic cubes, with a magnetic square slab between them to keep them in place. There is a cheaper version with black plastic cubes held together by a square frame.

The colour arrangements of the eight cubes are shown below, in no particular order.

1.	B
	G
R	W	P
	Y

2.	B
	G
P	W	Y
	R

3.	B
	G
R	Y	P
	W

4.	B
	G
W	Y	R
	P

5.	B
	G
W	P	R
	Y

6.	B
	G
Y	P	W
	R

7.	B
	G
P	R	Y
	W

8.	B
	G
Y	R	W
	P

My thanks to Puzzlemaniac for giving me this puzzle.

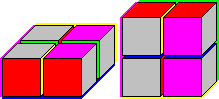
Solution:

The first solution:

	P
R	W	G	B
	Y

	P
G	W	Y	B
	R

	P
R	G	B	W
	Y

	P
B	G	Y	W
	R

	Y
R	P	G	B
	W

	R
G	P	Y	B
	W

	Y
R	G	B	P
	W

	R
B	G	Y	P
	W

The second solution:

	P
R	Y	W	B
	G

	P
W	R	Y	B
	G

	P
R	G	W	Y
	B

	P
W	G	Y	R
	B

	G
R	Y	P	B
	W

	G
P	R	Y	B
	W

	B
R	G	P	Y
	W

	B
P	G	Y	R
	W

The colour arrangement on the cubes is quite clever. Consider the following cube:

	P
R	G	Y	B
	W

Suppose you had 8 of the cubes above, stacked in a larger 2×2×2 cube so that the larger cube has the same colour arrangement on the outside, which matches that of the two Octacube solutions. The touching internal faces of these identical cubes obviously do not match in colour. Suppose that on four non-adjacent cubes (for example the top front right and back left cubes and the bottom front left and back right cubes) you cycle around the colours on their three internal faces in one direction, and on the remaining four cubes you cycle their three hidden colours in the other direction. This will cause the touching faces to match colour.

The procedure above produces one solution. If you had cycled all the hidden faces in the other direction, then you get the other solution. It turns out these are the only solutions, though this is not obvious.

I will now describe a quick method to find the solution.

Choose a colour, say blue. Place the cubes in a widely spaced row with the blue face on the bottom.

There is one colour that does not occur on any top face, i.e. which does not occur opposite blue. This is probably green. Turn all the cubes so that green is at the back (and blue remains at the bottom).

There are four colours that occur on the top faces, each on two cubes. Put the cubes with the same top colour next to each other, making four pairs of cubes. Make sure that in each pair the touching faces match in colour. If they don't, then swap the two cubes.

There are four pairs. Two pairs have red and yellow on the front, and the other two pairs have purple and white on the front. Put together the pairs that have the same front colours, so you have two 1×1×4 blocks. The touching faces will automatically match in colour.

In one of the 1×1×4 blocks, split it in half, turn one half upside down and place the other half on top to make a 1×2×2 block. The touching faces are all blue.
In the other 1×1×4 block, take the left and the right cubes, and place them back to front behind the middle cubes, making a 1×2×2 block. The new touching faces here are mostly green.

Put the two 1×2×2 blocks together to form the solved 2×2×2 cube.

Jaap's Puzzle Page

Octacube

The number of positions:

Solution: