Jaap's Puzzle Page

Port to Port / Triple Cross

Port to Port Triple Cross

Description
Port to Port Solution
Triple Cross Solution

Links to other useful pages:

ThinkFun homepage, the new name of the manufacturer Binary Arts.
David Barr's God's Algorithm software for Triple Cross.
Passion For Puzzles has images of the booklet which had a solution.

Description

These two puzzles have the same shape and mechanics, but have different designs. They have 18 tiles, which are moved by various plungers. The main area consists of a 2x7 rectangle and this can be moved one tile to the left or to the right (i.e. there are 3 positions; left, right and centre). There are also two small plungers which each hold a 3x2 rectangle of tiles, 4 of which are common to the main area. These plungers are connected so that if one is pushed upwards, the other is pushed downwards and vice versa.

This mechanism was invented by Ferdinand Lammertink, and patented on 6 August 1996, US 5,542,673.

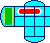
The Port to Port puzzle is the easiest of the two. Three of its tiles form a ship, and the aim is to move them from one side of the puzzle to the other. The other tiles are not important (four have a little boat on them, two form the Binary Arts logo, the rest are blank).

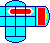
Triple cross is much more difficult because more tiles take part. Four tiles in a 2x2 square have one large circle on them. There are also three identical tiles with a horizontal line on them which should go together in any order in a 1x3 rectangle. As in Port to Port, there are two tiles with the Binary Arts logo. The start position has the circle on the far right, the line on the top left, the left plunger is pushed down and its bottom two tiles contain the logo. The aim is to restore these parts after the puzzle has been mixed.

These are tricky puzzles, because there are only a few possible moves and each one moves many tiles. Even Port to Port's ship is a little tricky to put together again once it has been broken up.

Port to Port

The number of positions:

All even permutations of the tiles are possible, but only the tiles that have part of the design on them matter. In Port to Port, only the three ship tiles matter, and these can be in 18·17·16 different positions. The plungers can only be in two different positions as I will only count positions with the main area centralised. Therefore there are only 2·18·17·16 = 9,792 positions.
Note that of these positions, there are 4 with the ship on one side and 4 with the ship on the other. Despite this low number, it is certainly not trivial. If you include the logo tiles, there are 2·18·17·16·15·14 = 2,056,320 positions.

I used computer searches to analyse the puzzles and to find good move sequences to use in the solutions. Ignoring the logo, there are no positions more than 33 moves away from being docked anywhere, 39 moves from being docked at the left side, 42 moves from being docked at the top left with the left plunger down, or 45 moves from being docked at the top left with the left plunger up.

If your browser supports JavaScript, you can play Port to Port by clicking this link:

JavaScript Port to Port Puzzle

Notation:

Let R and L denote moving the central area right and left respectively, and let / denote a movement of the plungers.

Solution to Port 2 Port:

There are 4 positions with the ship docked at the left port, and 4 with the ship in the right port. Therefore are 16 ways of crossing, but through symmetry there are only 6 essentially different ways. The following table shows all of the left to right crossings. The position of the ship and that of the plunger at that side is given. The shortest sequence is 29 moves.

Ship Plunger Sequence Ship Plunger
top down R/LL/R/L/R/R/L/L/R/R/L/R/LL/R (29) top down
top up /L/RR/L/L/R/R/LL/R/L/RR/L/R/L/ (30) top down
bottom up L/R/R/LL/R/L/RR/L/R/L/L/R/R/LL/R (32) top down
bottom down L/R/R/L/L/RR/L/R/LL/R/L/RR/L/R/L/ (33) top down
bottom down R/L/L/R/R/L/R/LL/RR/L/R/LL/R/R/LL/RR/L/ (39) bottom down
top up R/LL/RR/LL/R/R/L/R/LL/R/R/L/R/LL/R/R/L/L/R (42) bottom down

Here are the 4 essentially different ways to re-dock at the same port, i.e. keep the ship on the same side but change its position or the position of the plungers. The table below lists all these for a ship on the right hand side. The position of the ship and that of the plunger at that side is given.

Ship Plunger Sequence Ship Plunger
top up R/L/L/RR/L/L/R/ (15) top down
bottom up R/LL/RR/L/L/R/R/L/R/LL/R/ (25) top down
top up R/LL/R/R/LL/RR/L/L/R/R/L/ (25) bottom down
bottom down L/RR/L/L/R/R/L/R/L/R/LL/R/ (26) top down

There now follows a general method of moving/reassembling the ship in Port to Port. Denote each of the 18 tile positions by letters as shown in the following diagram.

QR
ABCDEFG
HIJKLMN
OP

The steps below will move the ship to the left, and reassemble it there. Start with the left plunger pushed down, and the main area centralised.

  1. If there is a ship tile in the right hand side, then
    1. Repeat sequence /L/R or its inverse L/R/ until positions D, E and K are empty, and there is a ship tile at Q, R, F, L or M.
    2. Repeat sequence /R/L or its inverse R/L/ until a ship tile lies at position D.
  2. Repeat step a until no ship tiles remain on the right hand side.
  3. Repeat sequence /L/R or its inverse L/R/ until positions D, K are empty.
  4. Consider the left and middle tiles of the ship. Repeat sequence /R/L or its inverse R/L/ until one of them lies at A, and the other does not lie at J.
  5. Repeat sequence /L/R or its inverse L/R/ until the left/middle tiles of the ship lie at A and B in either order.
  6. If the right tile of the ship lies at L then
    1. If the left tile of the ship lies at A then do /L/R/R/LL/R/R/L.
    2. If the middle tile of the ship lies at A then do L/R/R/LL/R/R/L.
  7. Do /R/L to leave the left/middle ship tiles at A and H.
  8. If the middle tile of the ship lies at A then
    1. If the right tile of the ship lies at J then do /R/L/R/L/L/RR/L/ to solve it.
    2. Otherwise repeat sequence L/R/ or /L/R till the right tile lies at position B and then do R/L/.
  9. If the left tile of the ship lies at A then
    1. If the right tile of the ship lies at J then do R/L/R/L/L/RR/L/ to solve it.
    2. Otherwise repeat sequence L/R/ or /L/R till the right tile lies at position O and then do /R/L/.

If you desperately want to recombine the logo tiles, then one method follows below. This assumes the ship lies at the top left, with the left plunger pushed down. The logo will be constructed at the bottom of the left plunger.

  1. Find the 'Binary' tile. To place it at O, do the relevant sequence in this list:
    D. R/LL/R/L/RR/L/L/R/L/R/R/LL/R/R/LL/RR/L
    E. /R/L/L/R/R/LL/R/R/LL/R/R/LL/R/R/L/R/L/
    F. /R/LL/RR/L/L/RR/L/R/LL/R/R/L
    G. R/L/L/R/L/RR/L/R/LL/R/L/RR/LL/RR/LL/R/
    H. /L/RR/LL/R/R/L/R/L
    I. L/RR/L/R/LL/RR/L/R/LL/RR/LL/R/
    J. R/L/R/LL/RR/LL/R/L/RR/L/R/LL/R
    K. /R/LL/R/L/RR/L/R/L/L/R/L/R/L/R/R/L
    L. L/RR/L/L/RR/L/L/RR/L/L/RR/L/
    M. L/RR/L/R/LL/R/R/L/R/L/R/L/
    N. R/L/L/RR/L/R/LL/R/R/LL/RR/L/
    P. R/LL/RR/LL/R/R/L/R/L/R/L
    Q. R/L/R/L/L/R/R/LL/RR/LL/RR/L/R/L/R/L/L/R/
    R. /L/RR/L/R/LL/RR/LL/RR/L/R/L/R/L/L/R/
  2. Find the 'Arts' tile. To place it at P, do the relevant sequence in this list:
    D. R/LL/R/R/L/R/L/R/LL/R/R/L/R/L/R/L/L/RR/L
    E. /R/LL/RR/LL/RR/LL/RR/LL/RR/L/R/LL/R/R/LL/R
    F. /L/R/R/LL/RR/L/L/RR/L/L/RR/L/L/RR/L/R/L/L/R/
    G. L/RR/L/l/R/L/R/L/RR/LL/RR/LL/R/R/L/R/L/L/R
    H. /L/RR/LL/R/R/L/L/RR/LL/R/R/LL/RR/LL/R/
    I. R/LL/R/R/L/R/L/R/L/L/RR/L/R/L/R/L/L/RR/L
    J. /R/L/R/L/R/LL/RR/LL/RR/L/R/L
    K. R/LL/RR/LL/RR/LL/RR/L/R/LL/R
    L. /R/L/R/LL/R/R/LL/RR/LL/R/R/L
    M. L/RR/L/R/LL/RR/LL/RR/LL/RR/L
    N. R/L/L/RR/L/R/L/L/RR/L/L/RR/LL/RR/L/L/RR/LL/R
    Q. R/L/L/RR/LL/RR/L/L/R/R/LL/RR/LL/RR/L/R/L
    R. L/R/R/L/L/RR/L/L/R/L/RR/L/R/L/R/LL/R/L/R/R/L

Triple Cross

Triple Cross

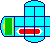
Triple cross is much more difficult than Port to Port because more tiles take part. Four tiles in a 2x2 square have one large red circle on them. There are also three identical tiles with a horizontal line on them which should go together in any order in a 1x3 rectangle. As in Port to Port, there are two tiles with the Binary Arts logo. The start position has the circle on the far right, the line on the top left, the left plunger is pushed down and its bottom two tiles contain the logo. The aim is to restore this exact position after the puzzle has been mixed.

There are actually a couple of different version of the puzzle, though they are equivalent. Instead of three tiles with a yellow line, there are versions with green dots on them instead. There are versions in which all the tiles and the frame are grey, and also ones with blue tiles and a purple frame.

The number of positions:

All even permutations of the tiles are possible, but only the tiles that have part of the design on them matter. In triple Cross, there are 9 viz. the 4 circle tiles, the 3 line tiles and the 2 logo tiles. These can be in 18!/(18-9)! positions. The three line tiles are indistinguishable so that leaves 18!/(18-9)!/3! different positions. I will only count positions with the main area centralised. The plungers can therefore be in two positions, which means the total number of positions for the puzzle is 2·18!/(18-9)!/3! = 5,881,075,200 positions.

If your browser supports JavaScript, you can play Triple Cross by clicking this link:

JavaScript Triple Cross Puzzle

Notation:

Let R and L denote moving the central area right and left respectively, and let / denote a movement of the plungers.
Denote each of the 18 tile positions by letters as shown in the following diagram.

QR
ABCDEFG
HIJKLMN
OP

Solution to Triple Cross:

This solution was constructed by using computer searches to find sequences that move specific tiles without moving others. This means it is mostly just lists of sequences without any visible underlying strategy. If anyone has a more transparent method, I would like to know about it.
Start with the left plunger pushed down, and the main area centralised.

Phase 1: Solve the circle.

  1. If there is a circle tile in the left hand side, then
    1. Repeat sequence /R/L or its inverse R/L/ until positions D, J and K have no circle tiles, and there is a circle tile at B, C, I, O or P.
    2. Repeat sequence /L/R or its inverse L/R/ until a circle tile lies at position K.
  2. Repeat step a until no circle tiles remain on the left hand side.
  3. Repeat sequence /R/L or its inverse R/L/ until positions D, K have no circle tiles. This might not be possible if both G and N have no circle tiles, so in that case first do /R/L or R/L/ until there is a circle tile at M but none at K, do /L/R, and then repeat this step.
  4. Consider the top right tile of the circle. If it lies at F then do the sequence R/L/L/R/L/R/R/LL/R, and repeat sequence /R/L or its inverse R/L/ until positions D, K have no circle tiles. Otherwise do /L/R or L/R/ till the top right tile is in position at G.
  5. Now consider the bottom right tile of the circle. If it is not in position at N then do the relevant sequence below:
    E. L/RR/LL/R/R/L/R/L/L/R/
    F. /R/L/L/R/L/R/R/LL/R/
    L. /R/LL/R/R/L/R/L/R/LL/R
    M. L/R/R/LL/R
    Q. /R/L/R/L/L/RR/L/L/R/L/R/
    R. R/LL/R/R/L/R/L/L/RR/LL/R
  6. Repeat sequence /R/L or its inverse R/L/ until there is a circle tile at M but none at D, K or L.
  7. If the bottom left circle tile is (correctly) positioned at M, then place the final circle piece using the relevant sequence the list below.
    E. /L/RR/L/R/LL/RR/LL/R/L/RR/LL/RR/L/R/L/
    Q. L/RR/LL/RR/LL/R/L/RR/LL/R/L/RR/L/L/R
    R. /L/R/L/R/R/LL/R/L/RR/L/L/R
    If the other circle tile lies at M, then one of the sequences below, depending on the position of the bottom left circle tile.
    E. L/R/L/R/L/RR/LL/RR/LL/R/L/R/R/L/
    F. /L/R/L/R/R/LL/R/L/RR/L/L/RR/L/
    Q. L/R/L/R/R/L/R/L/L/R/L/RR/L/L/R
    R. /R/L/R/LL/RR/LL/RR/L/L/R/L/R/L/R

Phase 2: Solve the line.

  1. Find a line piece that does not lie at position A, B or C.
  2. If C has no line piece, then do the relevant sequence below:
    D. /L/R/R/LL/R/R/LL/R/R/LL/R/R/L/
    E. L/R/R/LL/R/R/LL/R/R/LL/R/R/L
    H. L/RR/LL/R/R/LL/R/L/R/R/LL/R/R/LL/RR/LL/R/R/L
    I. /R/L/R/L/L/RR/L/L/R/L/RR/LL/R/R/LL/RR/L/L/R/R/LL/R
    J. R/L/L/R/R/L/L/R/R/L/L/R/R/L/L/R/
    K. /R/L/L/R/L/R/R/LL/RR/L/L/R/L/R/R/LL/R/
    L. /L/RR/L/L/R/L/R/R/LL/RR/L/L/R/L/R/R/L/
    O. /L/R/L/RR/LL/RR/L/L/R/R/LL/RR/L/L/R/R/LL/RR/LL/R
    P. /R/LL/R/L/R/R/LL/RR/L/L/R/L/R/R/LL/RR/L/R/L/
    Q. /L/R/R/L/L/R/R/L/L/R/R/L/L/R/R/L
    R. R/LL/R/R/L/L/R/R/L/L/R/R/L/L/R/R/L/R/L
  3. Otherwise, if B has no line piece, then do the relevant sequence below:
    D. R/L/R/L/L/R/R/L/L/R/R/L/L/R/R/L/L/RR/L
    E. L/RR/L/L/R/L/RR/L/L/RR/L/L/RR/L/L/RR/LL/R/R/LL/R
    H. L/R/L/R/R/L/L/R/L/RR/L/R/L/L/R/L/R/L/R/R/L/R/L
    I. R/L/R/L/R/LL/R/R/L/R/L/L/R/R/L/R/L/L/RR/L/R/L/
    J. /L/RR/L/L/R/R/L/L/R/R/L/L/R/R/L/L/R/L/R/
    K. /L/R/L/R/R/LL/R/R/LL/R/R/L/R/L/L/R/R/L/L/R/R/L
    L. L/R/L/R/R/L/R/L/L/R/L/RR/L/L/R/R/L
    O. R/L/L/R/R/LL/R/L/R/R/L/R/L/L/R/L/R
    P. L/R/R/LL/R/R/LL/R/R/L/R/LL/R/R/LL/R/R/LL/R/R/L/R/L
    Q. /L/R/L/R/L/R/R/L/R/L/L/R/L/R/L/R/R/L/L/R/R/L
    R. /L/R/L/R/R/L/L/R/R/L/L/R/R/L/L/R/R/LL/R/
  4. Otherwise, if A has no line piece, then do the relevant sequence below:
    D. R/LL/R/L/R/R/LL/RR/LL/R/R/L/L/R/R/LL/RR/L/L/R/L/R/R/LL/R
    E. L/RR/L/R/L/L/RR/LL/R/L/RR/LL/R/R/L/R/LL/R/L/R/
    H. /L/RR/LL/RR/L/L/RR/L/L/R/L/RR/L/L/RR/LL/RR/L
    I. R/LL/R/R/L/R/LL/R/R/LL/R/L/RR/L/L/RR/L/R/L/L/R
    J. /R/L/R/LL/R/L/R/R/L/L/R/R/L/L/R/R/L/L/R/R/LL/RR/L/
    K. /R/LL/RR/L/L/R/L/R/R/LL/RR/L/R/LL/RR/LL/R/L/R/L/R/
    L. R/L/L/R/R/L/L/R/L/R/L/R/R/L/R/L/L/R/L/R/L/R/
    O. L/R/R/L/R/L/L/R/L/R/R/L/R/L/L/RR/L/L/R/L/R/R/L
    P. /R/L/R/LL/R/R/L/R/L/L/R/R/L/R/L/L/RR/L/R/L/R/L
    Q. /R/L/L/R/L/RR/L/L/RR/LL/RR/LL/RR/LL/RR/L/R/LL/R/L/R/
    R. R/LL/RR/LL/R/R/LL/R/L/R/R/LL/R/R/LL/RR/LL/R/
  5. Repeat the above till all three line pieces are at A, B or C.

Phase 3: Solve the logo.

  1. Find the 'Binary' logo tile, and do the relevant sequence below to place it at position O.
    D. L/RR/L/L/R/L/R/R/L/L/R/R/L/L/R/R/L/L/R/R/LL/R/R/LL/R
    E. L/RR/L/R/L/R/LL/RR/L/L/R/L/RR/L/R/L/L/RR/L/L/R/L/R/L/R/R/L
    H. /R/LL/RR/L/R/L/L/RR/L/R/LL/R/R/L/R/LL/R/R/LL/R/L/R
    I. /R/LL/RR/LL/RR/L/L/R/L/R/R/LL/RR/L/L/R/L/R/L/RR/L/
    J. /R/L/L/R/R/LL/RR/L/L/R/L/R/R/LL/RR/L/L/RR/L/
    K. /R/LL/R/R/LL/RR/L/L/R/L/R/R/LL/RR/L/L/R/R/L/
    L. /R/L/R/L/L/RR/L/L/R/R/L/L/R/R/L/L/R/R/L/L/R/L/R/R/L/R/L/
    P. L/R/R/L/L/R/R/L/L/R/L/RR/L/L/R/L/R/R/LL/RR/L/L/RR/L/
    Q. /L/RR/LL/R/R/L/R/LL/R/L/RR/L/L/R/L/R/L/RR/L/L/R/L/R/R/LL/R/R/L
    R. /R/LL/R/L/R/L/R/R/LL/RR/L/L/R/L/R/R/LL/RR/LL/RR/L/
  2. Find the 'Arts' logo tile, and do the relevant sequence below to place it at position P.
    D. L/RR/L/L/R/L/RR/LL/RR/LL/RR/LL/RR/LL/RR/L/L/R/R/LL/R
    E. /L/RR/L/L/R/L/R/R/LL/R/L/R/R/L/L/R/R/L/R/L/L/RR/L/L/R/
    H. /L/R/R/LL/R/R/L/R/L/L/R/R/L/L/R/L/RR/L/L/R/L/R/R/LL/R/
    I. L/RR/L/L/R/R/LL/RR/LL/RR/LL/RR/LL/RR/LL/R/L/R/R/LL/R
    J. /R/L/L/R/R/L/L/R/R/L/L/R/R/L/L/R
    K. /L/R/R/L/R/L/L/R/R/L/L/R/R/L/L/R/R/L/L/RR/L/L/R/
    L. L/R/R/L/L/R/R/L/L/R/R/L/L/R/R/L/
    Q. R/L/L/RR/L/L/R/L/R/R/L/L/R/R/L/L/R/R/L/L/R/R/LL/R/R/LL/R/R/L
    R. L/RR/LL/RR/LL/R/L/R/L/RR/L/L/RR/L/L/RR/L/L/RR/LL/R/L/RR/LL/RR/LL/R