



The Great Pyramid Puzzle is a puzzle consisting of a tetrahedral body, and 36 loose triangular tiles that are coloured with red and white patterns. The tiles can be stuck onto the tetrahedron, nine tiles on each face, because every tile has a peg in its centre and the tetrahedron has holes they fit into. The aim is to cover the tetrahedron with the tiles such that all adjacent tiles match along their common edge.
There is also a smaller version with 4 tiles on each face, 16 tiles all together, which is called the Great Pyramid Pocket Puzzle.
The tiles are regular triangles, which are split into 12 segments by 6 lines - the 3 bisectors and 3 lines parallel to the sides. The four segments along each side are coloured either red or white. The following pictures show all the tiles of both puzzles:
The Great Pyramid Puzzle: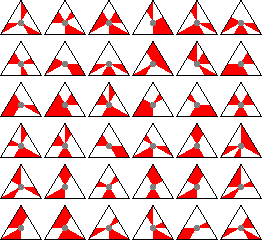
The Great Pyramid Pocket Puzzle:
The puzzles were made by Eliot Inventions Ltd. in 1981. The pocket puzzle comes in a neat transparent plastic box that opens in an unusual way. The large pyramid puzzle has a metal stand, giving you easy access to all the sides.
There was a competition associated with the Great Pyramid puzzle. For each puzzle sold in the UK,
one pound was placed in a prize fund account. On 10 September 1982, all entries would be examined in
order of receipt, and the first entrant with a correct solution would win the prize fund. Interest
on the fund account went to charity. If there were no correct entries, the competition would remain
open till the first correct entry was received. If no winner was found by 31 December 1999, the
whole prize fund would go to charity. The size of the prize fund would be published on the first
Monday of every month in the personal columns section of the Times.
The notice printed in the Times on 6 December 1982 stated that £21,480 was paid to the
winner, and that £1,731 went to charity.
The puzzle's 36 tiles can be ordered in 36! ways. Two tiles have rotational
symmetry, the rest have 3 visibly different orientations so they can be oriented
in 334 ways.
A tetrahedron has 12 orientations, so the Great Pyramid Puzzle has 36!·334/12
= 5.1698·1056 possible arrangements for the tiles.
The pocket puzzle's 16 tiles can be arranged in 16! ways, and oriented in 316 ways.
The Pocket Puzzle therefore has 16!·316/12 = 75,054,791,570,863,104,000
possible arrangements for the tiles.
This is of course not a realistic measure of difficulty, since you would not continue placing tiles
after one tile is wrongly positioned.
One of the many solutions to the Great Pyramid Puzzle is shown below.

I used my computer to find all solutions of the Pocket puzzle, and there are 87 of them.They are all shown below. To save space, if some solutions differ only by two or three tiles then only one of them is shown and the relevant tiles are given a different colour. The number of solutions represented by the drawing is also given.
