


Peg Solitaire, sometimes sold as Hi-Q, is a classic peg-jumping puzzle. It consists of a board with 33 holes, arranged in the shape of a cross - a 3×3 square with four 2×3 rectangles added to its sides. At the start, all but the centre hole contains a peg. A move consists of jumping one peg over another to land in a vacant hole, and then removing the peg that was jumped over. At the start of the move, the jumping peg, the peg jumped over, and the landing hole must be adjacent and lie in a straight line. The aim of the puzzle is to remove all but one of the pegs, and preferably to leave that final peg in the centre of the board.
I don't think there is any way to calculate this directly. Instead I have written a computer program to enumerate all the reachable positions. The results are shown in the table below.
| Starting hole at | |||||||
|---|---|---|---|---|---|---|---|
| Jumps | d4 | d5 | d6 | d7 | c5 | c6 | c7 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 4 | 4 | 1 | 1 | 4 | 2 | 2 |
| 2 | 12 | 15 | 6 | 3 | 18 | 8 | 6 |
| 3 | 60 | 74 | 29 | 15 | 86 | 46 | 29 |
| 4 | 296 | 362 | 144 | 77 | 433 | 230 | 147 |
| 5 | 1,338 | 1,657 | 669 | 366 | 2,000 | 1,079 | 731 |
| 6 | 5,648 | 7,085 | 2,907 | 1,635 | 8,727 | 4,816 | 3,404 |
| 7 | 21,842 | 27,827 | 11,528 | 6,740 | 34,889 | 19,637 | 14,551 |
| 8 | 77,559 | 99,457 | 41,688 | 25,495 | 126,531 | 72,360 | 56,671 |
| 9 | 249,690 | 320,728 | 137,130 | 87,357 | 413,940 | 240,412 | 198,784 |
| 10 | 717,788 | 922,771 | 404,721 | 267,748 | 1,207,725 | 713,626 | 621,426 |
| 11 | 1,834,379 | 2,346,137 | 1,063,088 | 729,543 | 3,112,769 | 1,876,329 | 1,713,327 |
| 12 | 4,138,302 | 5,231,358 | 2,473,311 | 1,755,981 | 7,016,324 | 4,332,867 | 4,128,222 |
| 13 | 8,171,208 | 10,140,538 | 5,052,961 | 3,703,898 | 13,691,570 | 8,707,596 | 8,605,721 |
| 14 | 14,020,166 | 16,962,675 | 8,996,006 | 6,793,053 | 22,931,476 | 15,102,419 | 15,381,583 |
| 15 | 20,773,236 | 24,370,107 | 13,871,043 | 10,761,539 | 32,749,346 | 22,445,872 | 23,406,926 |
| 16 | 26,482,824 | 30,010,119 | 18,414,714 | 14,643,000 | 39,743,305 | 28,443,075 | 30,188,034 |
| 17 | 28,994,876 | 31,702,230 | 20,985,971 | 17,054,786 | 41,081,942 | 30,699,210 | 32,991,221 |
| 18 | 27,286,330 | 28,854,923 | 20,527,646 | 16,981,596 | 36,420,647 | 28,337,649 | 30,700,024 |
| 19 | 22,106,348 | 22,716,967 | 17,257,832 | 14,478,582 | 27,865,545 | 22,501,128 | 24,480,322 |
| 20 | 15,425,572 | 15,487,869 | 12,474,155 | 10,595,121 | 18,471,677 | 15,423,736 | 16,795,327 |
| 21 | 9,274,496 | 9,151,588 | 7,745,937 | 6,663,269 | 10,624,895 | 9,145,500 | 9,936,310 |
| 22 | 4,792,664 | 4,683,233 | 4,129,039 | 3,594,343 | 5,298,785 | 4,687,990 | 5,067,365 |
| 23 | 2,120,101 | 2,065,635 | 1,880,351 | 1,656,611 | 2,280,236 | 2,068,914 | 2,217,560 |
| 24 | 800,152 | 780,211 | 728,129 | 650,342 | 840,445 | 781,688 | 828,091 |
| 25 | 255,544 | 250,415 | 238,654 | 216,129 | 263,204 | 250,283 | 261,848 |
| 26 | 68,236 | 67,006 | 64,950 | 59,910 | 68,782 | 66,861 | 68,988 |
| 27 | 14,727 | 14,493 | 14,262 | 13,503 | 14,755 | 14,574 | 14,710 |
| 28 | 2,529 | 2,562 | 2,551 | 2,395 | 2,615 | 2,604 | 2,570 |
| 29 | 334 | 345 | 345 | 329 | 346 | 346 | 345 |
| 30 | 32 | 29 | 29 | 32 | 24 | 24 | 29 |
| 31 | 5 | 4 | 4 | 5 | 3 | 3 | 4 |
| Total | 187,636,299 | 206,218,425 | 136,519,802 | 110,743,405 | 264,273,045 | 195,940,885 | 207,684,279 |
| Avg Depth | 17.093 | 16.906 | 17.341 | 17.468 | 16.785 | 17.031 | 17.106 |
For further analysis techniques, see the Analysis of Peg Solitaire page.
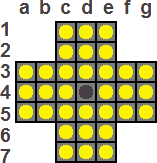
I will label the rows from top to bottom with the numbers 1 to 7, and the columns from left to right with the letters a to g. Every board location then can be denoted by its coordinates, e.g. d4 is the central hole. Any jump can be described by two coordinates, of the start and end hole of the jump, e.g. b4-d4 for a jump to the right into the centre hole.
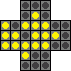
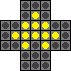
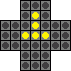
Here is one of the best known solutions, which is easy to memorise.
| First move | Clear first arm |
Clear second arm |
Clear third arm |
Clear fourth arm |
Break down the house |
Finish |
|---|---|---|---|---|---|---|
| d6-d4 |
f5-d5 e7-e5 c7-e7 e4-e6 e7-e5 |
e2-e4 g3-e3 g5-g3 d3-f3 g3-e3 |
b3-d3 c1-c3 e1-c1 c4-c2 c1-c3 |
c6-c4 a5-c5 a3-a5 d5-b5 a5-c5 |
d3-b3 b3-b5 b5-d5 d5-f5 f5-f3 f3-d3 |
d4-f4 d2-d4 c4-e4 f4-d4 |
 |
 |
 |
 |
 |
 |
 |
Note that the set of moves for clearing each arm is essentially the same, so after doing the five moves to clear the first (bottom) arm, you can rotate the board clockwise, and repeat the exact same five moves for the next arm, which is now at the bottom. The same procedure can be done for the other two arms.
Here are other solutions, taken from the book The Ins and Outs of Peg Solitaire by John D. Beasley.
| Start | End | Moves | ||
|---|---|---|---|---|
| d4 | d1 | d6-d4 | b5-d5 c7-c5 c4-c6 e7-c7 c7-c5 d5-b5 c2-c4 a3-c3 c4-c2 b5-b3 a5-a3 a3-c3 d3-b3 f3-d3 e1-e3 d3-f3 c1-c3 b3-d3 g3-e3 d3-f3 g5-g3 g3-e3 d1-d3 f5-d5 e3-e5 | e6-e4 d4-d2 f4-d4 d5-d3 d3-d1 |
| d7 | d1 | d5-d7 | ||
| d4 | d4 | d6-d4 | e6-e4 d4-d6 f4-d4 d3-d5 d6-d4 | |
| d7 | d4 | d5-d7 | ||
| d4 | d7 | d6-d4 | e6-e4 d4-d6 f4-d4 d3-d5 d5-d7 | |
| d7 | d7 | d5-d7 | ||
| d4 | g4 | d6-d4 | e5-c5 d3-d5 c5-e5 e6-e4 e4-g4 | |
| d7 | g4 | d5-d7 | ||
| c2 | c2 | c4-c2 | a3-c3 c2-c4 a5-a3 b5-b3 a3-c3 c4-c2 c1-c3 d3-b3 e1-c1 e2-c2 c1-c3 b3-d3 e4-e2 g3-e3 e2-e4 g5-g3 f5-f3 g3-e3 d5-f5 e7-e5 f5-d5 c7-e7 c6-e6 e7-e5 e4-e6 c5-e5 e6-e4 | e4-c4 e3-c3 c4-c2 |
| c5 | c2 | c3-c5 | ||
| c2 | c5 | c4-c2 | e4-c4 e3-c3 c3-c5 | |
| c5 | c5 | c3-c5 | ||
| c2 | f5 | c4-c2 | d3-d5 e3-e5 d5-f5 | |
| c5 | f5 | c3-c5 | ||
| d2 | d2 | d4-d2 b3-d3 b4-d4 | c1-c3 d3-b3 e1-c1 e2-c2 c1-c3 b3-d3 e4-e2 g3-e3 f5-f3 g5-g3 e2-e4 g3-e3 d5-f5 e7-e5 f5-d5 c6-c4 a5-c5 d5-b5 a3-a5 a5-c5 c4-c6 c7-c5 d7-d5 | c5-e5 d3-f3 e5-e3 f3-d3 d4-d2 |
| d5 | d2 | d3-d5 b3-d3 b4-d4 | ||
| a5 | d2 | c5-a5 b3-b5 c3-c5 | ||
| d2 | d5 | d4-d2 b3-d3 b4-d4 | e3-e5 d5-f5 d3-d5 c5-e5 f5-d5 | |
| d5 | d5 | d3-d5 b3-d3 b4-d4 | ||
| a5 | d5 | c5-a5 b3-b5 c3-c5 | ||
| d2 | g5 | d4-d2 b3-d3 b4-d4 | e3-e5 d5-f5 d3-d5 c5-e5 e5-g5 | |
| d5 | g5 | d3-d5 b3-d3 b4-d4 | ||
| a5 | g5 | c5-a5 b3-b5 c3-c5 | ||
| d2 | a5 | d4-d2 b3-d3 b4-d4 | e3-e5 d5-b5 d3-d5 e5-c5 c5-a5 | |
| d5 | a5 | d3-d5 b3-d3 b4-d4 | ||
| a5 | a5 | c5-a5 b3-b5 c3-c5 | ||
Note that if, for example, you want to start at g4 and finish at d7, then you can do the inverse of the d7 to g4 solution above. These solutions, together with their inverses, rotations, and mirror images, can supply a solution for any solvable combination of starting hole and final peg location.
For further analysis techniques for this and other peg solitaire games, see the Analysis of Peg Solitaire page.