


Solo is a version of Peg Solitaire. Instead of pegs however, it has balls that are mounted inside a frame. The balls are black one side, white on the other, and can be rotated in place to show either of those colours to represent the presence or absence of a peg. The board is based on a rectangular grid, and the number of balls in each row from top to bottom are 7, 9, 9, 7, 5, 3, and 1, centred so its shape looks like a cut diamond.
For further analysis techniques, see the Analysis of Peg Solitaire page.
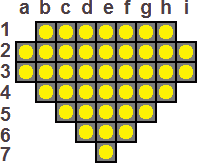
Hold the puzzle with the sharp 90 degree corner at the bottom. I will label the rows from top to bottom with the numbers 1 to 7, where row 7 has just one ball, and the columns from left to the right with the letters a to i. Every board location then can be denoted by its coordinates, e.g. the bottom corner is e7. Any jump can be described by two coordinates, of the start and end hole of the jump, e.g. e7-e5 for a jump from the bottom corner upwards.
This is rather difficult puzzle, due to it not having many straight edges.
Here are some solutions.
| Start | End | Moves | ||
|---|---|---|---|---|
| d3 | c3 | f3-d3 e5-e3 f5-f3 | e7-e5 h4-f4 f3-f5 f6-f4 d5-f5 d3-d5 d6-d4 g5-e5 e2-e4 e5-e3 g2-g4 i2-g2 g1-g3 g4-g2 i3-g3 e1-g1 h1-f1 c2-e2 c1-e1 a2-c2 c3-c1 b1-d1 a3-c3 f1-f3 f3-d3 d4-d2 b4-d4 d1-d3 g2-g4 g4-e4 e4-c4 d3-b3 c5-c3 b3-d3 e1-e3 | e3-c3 |
| d6 | c3 | f6-d6 e4-e6 f4-f6 | ||
| g3 | c3 | e3-g3 e5-e3 f5-f3 | ||
| d3 | f3 | f3-d3 e5-e3 f5-f3 | d3-f3 | |
| d6 | f3 | f6-d6 e4-e6 f4-f6 | ||
| g3 | f3 | e3-g3 e5-e3 f5-f3 | ||
| d3 | i3 | f3-d3 e5-e3 f5-f3 | e7-e5 e2-e4 e5-e3 c4-e4 c2-c4 d6-d4 c5-c3 h4-f4 f3-f5 f6 f4 e4-e2 e2-c2 d4-d2 d1-d3 c2-c4 b4-d4 a3-c3 a2-c2 b1-d1 g2-e2 e1-e3 c3-c1 c1-e1 d4-d2 f1-d1 d1-d3 d3-f3 h1-f1 f4-f2 f1-f3 i2-g2 g2-g4 i3-g3 f3-h3 g5-g3 g3-i3 | |
| d6 | i3 | f6-d6 e4-e6 f4-f6 | ||
| g3 | i3 | e3-g3 e5-e3 f5-f3 | ||
| d6 | f6 | d4-d6 f5-d5 e7-e5 d6-d4 d3-d5 b3-d3 c5-c3 d3-b3 d1-d3 b1-d1 a3-c3 c2-c4 b4-d4 a2-c2 f3-f5 f6-f4 d5-f5 h3-f3 g5-g3 f3-h3 f1-f3 h1-f1 i3-g3 g2-g4 i2-g2 f4-f2 f1-f3 e1-c1 c1-c3 e3-e5 c3-e3 e3-g3 h4-f4 g2-g4 g4-e4 e5-e3 e2-e4 d4-f4 f4-f6 | ||
| a3 | i3 | c3-a3 b1-b3 a3-c3 d2-b2 a2-c2 d4-d2 b4-d4 c2-c4 c5-c3 e4-c4 d6-d4 f5-d5 e7-e5 d5-f5 c4-c2 c1-c3 f3-d3 c3-e3 d1-d3 d4-d2 g4-e4 f6-f4 g2-g4 f1-f3 h1-f1 e1-g1 d2-f2 i2-g2 i3-g3 f3-f5 h4-f4 g2-g4 g5-g3 f5-f3 e4-e2 e2-g2 f3-h3 g1-g3 g3-i3 | ||
| d3 | f6 | Mirror and inverse of d6-f3 | ||
| g3 | f6 | Mirror and inverse of d6-c3 | ||
| a3 | f3 | Mirror and inverse of d3-i3 | ||
| a3 | f6 | Mirror and inverse of d6-i3 | ||
| a3 | c3 | Mirror and inverse of g3-i3 | ||
| b1 | e2 | d1-b1 c3-c1 d3-d1 | a3-c3 a2-c2 f2-d2 d1-d3 b1-d1 d3-b3 b4-b2 b2-d2 c5-c3 e4-c4 d6-d4 f5-d5 e7-e5 d5-f5 g4-e4 f6-f4 g2-g4 i2-g2 i3-g3 f3-h3 h4-h2 h1-h3 g5-g3 h3-f3 g1-g3 d1-d3 f1-d1 d4-d2 d1-d3 c4-c2 f4-d4 d4-d2 c2-e2 e2-e4 g3-e3 | e4-e2 |
| e1 | e2 | c1-e1 c3-c1 d3-d1 | ||
| b4 | e2 | d4-b4 c2-c4 d2-d4 | ||
| e4 | e2 | c4-e4 c2-c4 d2-d4 | ||
| b1 | e5 | d1-b1 c3-c1 d3-d1 | e3-e5 | |
| e1 | e5 | c1-e1 c3-c1 d3-d1 | ||
| b4 | e5 | d4-b4 c2-c4 d2-d4 | ||
| e4 | e5 | c4-e4 c2-c4 d2-d4 | ||
| b1 | h2 | d1-b1 c3-c1 d3-d1 | a3-c3 a2-c2 f2-d2 d2-b2 b1-b3 b4-b2 f3-d3 c3-e3 c5-c3 e4-c4 c4-c2 b2-d2 d6-d4 f5-d5 e7-e5 d1-d3 f1-d1 c1-e1 h1-f1 d3-f3 f3-f5 f6-f4 d5-f5 g4-e4 d4-f4 f5-f3 g2-g4 i2-g2 i3-g3 f3-h3 e1-g1 g5-g3 h3-f3 g1-g3 f3-h3 h4-h2 | |
| b4 | h2 | d4-b4 c2-c4 d2-d4 | ||
| b1 | b2 | d1-b1 c3-c1 d3-d1 | f3-d3 f1-f3 h1-f1 f4-f2 f1-f3 h4-f4 g2-g4 i2-g2 i3-g3 f4-h4 g2-g4 h4-f4 e4-g4 g5-g3 g3-e3 f6-f4 d5-f5 e7-e5 f5-d5 c4-e4 d6-d4 d4-d2 d1-d3 b1-d1 e1-c1 a2-c2 a3-c3 f4-d4 c2-c4 c5-c3 e2-e4 e4-c4 c4-c2 c1-c3 d3-b3 b4-b2 | |
| b4 | b2 | c1-e1 c3-c1 d3-d1 | ||
| e1 | b2 | d4-b4 c2-c4 d2-d4 | ||
| e4 | b2 | c4-e4 c2-c4 d2-d4 | ||
| e7 | b2 | e5-e7 e3-e5 g4-e4 f6-f4 f3-f5 e5-e3 g5-e5 g2-g4 e2-e4 h4-f4 e4-e6 c5-e5 d3-d5 d5-f5 e7-e5 f5-d5 d6-d4 f1-f3 f4-f2 c2-e2 i3-g3 i2-g2 h1-f1 f1-f3 g3-g1 d1-f1 g1-e1 e1-e3 f3-d3 d4-d2 b1-d1 d1-d3 a2-c2 b4-d4 c2-c4 a3-c3 | c4-c2 d4-d2 d2-b2 | |
| e7 | e2 | c4-c2 d4-d2 c2-e2 | ||
| e7 | e5 | c3-c5 d3-d5 c5-e5 | ||
Note that if, for example, you want to start at e2 and finish at b1, then you can do the inverse of the b1 to e2 solution above. These solutions, together with their inverses, and mirror images, can supply a solution for any solvable combination of starting hole and final peg location.
For further analysis techniques for this and other peg solitaire games, see the Analysis of Peg Solitaire page.