Swissmad is a puzzle with 12 square tiles arranged the shape of a cross. The tiles are contained in a flat frame which has transparent front and back plates, so that both sides of the tiles are visible. The cross has a 2 by 2 square in the centre and arms 2 tiles wide and one tile long. The two columns of the vertical arms can slide up or down one tile, independently of each other, by pushing the two parts of the transparent front plate of the puzzle up or down. Similarly, the two rows of the horizontal arms of the cross can individually slide left or right by pushing the transparent back plate sections left or right.
Each tile is red or white on the front and red or white on the back. This gives four possible tile types, and there are exactly three of each type of tile. In the standard solved position the back of the cross is half white and half red, while the front of the cross is in quarters of alternating colour.
Embossed on the frame are eight patterns that you can try to make. I reproduce them below with the names they have been given in the leaflet.
 Time |
 Interaction |
 Excellence |
 Balance |
 Diversity |
 Audacity |
 Mutual help |
 Security |
The leaflet quite amusingly tries to justify the names of these patterns. The leaflet itself is also in the shape of a cross, normally with the arms folded over to make it square. The arms of this leaflet show the patterns 'Time', 'Excellence', 'Balance' and 'Diversity', so by changing the order in which you fold these arms, you can have any of these patterns on the front. By some clever folding, you can however also get it to show the 'Mutual help' pattern instead.
Swissmad was invented by Olivier Pahud, and patented on 16 June 2005, WO 2005/053809.
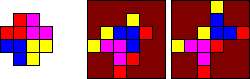
There is a very rare version of the puzzle with four colours. It has a grey frame and the
pieces are yellow, green, black, and purple. Every combination of front and back
colours occurs exactly once. If each quadrant on the front has one colour, there are only
six fully symmetric patterns the back can have. These are shown in the picture on the right.
The first of these, with each colour on a diagonal line is normally considered the goal.
If your browser supports JavaScript, then you can play with Swissmad by clicking the link below:
The packaging states "Two faces, two colours, one million combinations". As you will see, this is not quite accurate. Lets assume the rows and columns are centred. There are 12 pieces, in four sets of identical triplets. These can be arranged in 12!/3!4 = 369,600 positions. If you don't assume the rows and columns are centred, then this number must be multiplied by 34 because each row/column has 3 states. Then there are 12!·34 / 3!4 = 29,937,600 positions.
I have used a computer search to find God's Algorithm, i.e. the shortest solution for each position. The result is shown in the tables below.
| Multiple Tile Metric | Single Tile Metric | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
This shows that if pushing a slide from one extreme to another is considered a single move,
then the Swissmad takes at most 21 moves to solve (14.519 on average). If that is counted two
moves, then it takes 28 moves at most (18.074 on average). All this assumes that you are working
towards one particular solved position that has a Time/Time or Time/Diversity pattern. Other
patterns may give slightly different results. The antipodal positions for each metric are unique
up to rotation, and are shown on the right using four colours to represent the four types of tile.
The table shows which combinations of the eight patterns can be put on the front and back of the puzzle.
| Front |  |
Back | |||||||
| Time | Interaction | Excellence | Balance | Diversity | Audacity | Mutual help | Security | ||
|
|||||||||
Time |
 |
 |
|
|
|
|
|
||
|
|||||||||
Interaction |
|
|
|
|
|
|
 |
|
|
|
|||||||||
Excellence |
|
|
 |
 |
|
|
|
||
|
|||||||||
Balance |
|
|
|
|
|
|
|
|
|
|
|||||||||
Diversity |
|
|
|
|
|
||||
|
|||||||||
Audacity |
|
|
|
|
|
||||
|
|||||||||
Mutual help |
|
|
|
|
|
|
|||
|
|||||||||
Security |
|
|
|
|
|
||||
There is a very simple sequence of four moves that cycles three pieces around. Slide a column down, a row to the right, the column back up, and finally the row back to the left. The three pieces that are moved are the tile at the intersection of the row and column, as well as the tile above and the tile to the left.
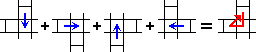
Any three adjacent tiles that do not lie in a straight line but in a kind of L formation, any such three tiles can be cycled around. Simply shift the row and column alternately to push the two outside tiles towards the middle one, and then move the row and column back. Using this sequence it is quite easy to solve any position.
To solve a position, the best general strategy is to first solve the arms of the cross one by one. With the move sequence you can move any tile from an arm into the central area, then move it around the central area to the side you want, and finally move it out into an arm of the cross. Once all the arms are correct it is usually an easy matter to solve the central area. Always remember to check both sides of the tile are correct for the spot you are moving it to.
One minor complication that can arise with this method is that you may end up needing to swap two pieces without moving anything else. This usually happens when all the arms have been solved, and the central area contains all four types of tiles. In this case replace any tile on an arm by the identical one from the central area. After this, the puzzle can be solved easily.
When solving the standard pattern (time/diversity), I usually do things differently. I solve the 'time' side first, putting all the reds in one half, all the whites in the other. When doing this I don't need to worry about the other side of the puzzle. Then I turn it over and separate each of those halves again, into red and white quarters. By never letting any tile from the other half enter the half you are solving, the 'time' pattern on the back will not be disturbed. The advantage of this method is that you don't need to keep track of the reverse colours of the tiles at all.