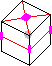
8. Symmetry r4r2, <(1234), (24)>, 8.

We can hold the cube so that the 90 degree symmetry is around the U-D axis. Lets consider the corners first. The same arguments as in 5 apply, so the corners cannot be twisted. If they move about in the same U/D layer, then they must all move in the same way, either in a 4-cycle, or in swaps with opposite pairs in their layer. This time there is no reflectional symmetry so the 4-cycles are not ruled out.

1. Two 4-cycles of corners, type 1 (UFR,ULF,UBL,URB)(DRF,DBR,DLB,DFL)
   Fs2 Rs2 U Fs2 Rs2 D (10f*,18q*)

The corners can again swap U/D layers. There are two new possibilities: each corner swaps with the one a quarter turn to its right in the other layer, or they swap with those to the left.

2. 4-swap of corners, type 3 (URF,DRB)(UFL,DFR)(ULB,DLF)(UBR,DBL)
   F2 R2 Ua' (R2 F2)² Ua F2 R2 (12f*)
   (F2 R2)² D2 F2 U2 (F2 R2)² U2 F2 D2
3. 4-swap of corners, type 4 (URF,DLF)(UFL,DBL)(ULB,DRB)(UBR,DFR)
   F2 R2 Ua (R2 F2)² Ua' F2 R2 (12f*)
   (F2 R2)² U2 F2 D2 (F2 R2)² D2 F2 U2

Note that 8c is the same as combining 8a and 8b and a pattern from section 5. The permutations 8a and 8b do not commute, i.e. 8a+8b is not the same as 8b+8a. (In fact, x=8a has order 4, y=8b has order 2, xy=yx^-1 so x,y generate a group isomorphic to the dihedral group D₄, the symmetries of the square.)

Now consider the edges. The edges can only be flipped in the same way as in section 5. The middle edges have no new possible movements. This time however the movement of the U/D edges, like the corners, also allows 4-cycles in the U/D layers, or swaps with any of the edges in the opposite layer. This gives three new edge patterns.

4. Two 4-cycles of edges, type 1 (UF,UR,UB,UL)(DF,DL,DB,DR)
   Fs2 Rs2 U Fs2 Rs2 U' (10f*)
5. 4-swap of edges type 1 (UR,DF)(UF,DL)(UL,DB)(UB,DR)
   (D' Rs2 U)² (8f*,12q*)
6. 4-swap of edges type 2 (UR,DB)(UF,DR)(UL,DF)(UB,DL)
   D Rs2 Us' Rs2 U' (8f*,12q*)

Note that 8f is the same as combining 8d and 8e and a pattern from section 5.

These patterns (together with those in section 5) form a group of order 512 (isomorphic to D₄²×C₂³). The only new nice patterns are those that only involve 8b (or 8c) in combination with patterns of section 5, because all others have 3 colours on some faces.

7. 2+, 4 diagonals [p18] (5o+8b)
   (Fa Ra3)³ (12f*,12q*)
   (F2 R2)² (D2 F2)² L2 F2 L2 U2 B2 D2
8. 2O, 4 diagonals [p63] (5r+8b)
   B2 R2 Ua' L2 F2 R2 B2 Ua F2 L2 (12f*)
   (F2 R2)² (U2 B2)² R2 F2 L2 U2 F2 D2
9. 2+, vertical 4S [p199] (5i+8b)
   Ra' Fa' Ra' Fa Ra Fa (12f*,12q*)
   (F2 R2)² (U2 F2)² L2 F2 L2 D2 B2 D2
10. 2O, vertical 4S (5l+8b)
    B2 L2 Ua L2 F2 L2 F2 Ua' F2 R2 (12f*)
    (F2 R2)² (U2 B2)² R2 F2 L2 U2 F2 U2
11. 2+, horizontal 4S (5g+8b)
    F2 R2 Ua' L2 F2 R2 B2 Ua F2 R2 (12f*)
    (F2 R2)² (D2 B2)² L2 B2 L2 U2 F2 D2
12. 2O, horizontal 4S [p111] (5h+8b)
    B2 L2 Ua' L2 B2 R2 F2 Ua F2 R2 (12f*)
    (F2 R2)² (D2 F2)² R2 B2 L2 D2 B2 U2
13. 2O, 4 Deuce (5f+8b)
    B2 L2 Ua' R2 B2 R2 B2 Ua F2 R2 (12f*)
    (R2 F2)² (D2 R2)² F2 L2 B2 D2 L2 D2

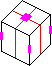
9. Symmetry m_cr2_er2_e, <(13), (24), i>, 8.

Suppose the r2 symmetries are centred around the middle layer edges, and that a plane of reflectional m symmetry goes through the centre point. Note that the reflection through the middle layer (m_f) also lies in this symmetry group, as well as the vertical planes m_e.

The corners occur in two orbits; the URF, DFR, ULB, DBL corners form one orbit, the remainder the other. They can be moved by two (disjoint) swaps in three ways:

1. 2-swap of corners, type 1 [p75/p77] (URF,ULB)(DFR,DBL)
   Us2 L2 F R2 Us2 L2 B R2 (10f*)
   U2 L2 F2 L2 U2 F2 (U2 L2)³ F2
2. 2-swap of corners, type 2 (URF,DBL)(ULB,DFR)
   R2 B2 R2 U L2 U' R2 B2 R2 D F2 D' (12f*)
3. 2-swap of corners, type 3 (9a+9b) (URF,DFR)(ULB,DBL)
   D R2 Ua R2 F2 R2 F2 D2 R2 F2 R2 U' (13f*)

If a corner were to move anywhere else, the symmetry would be broken. The 4 corners in an orbit must all twist the same way, due to the r2 symmetries, but the reflectional symmetry does not allow this.

An edge in the U/D layers can be moved to any other position in the U/D layer, and this then fixes the movement of the other U/D edges. Three such movements have been seen in 5f-h, and here are two more (which occur in two orientations around the U/D axis). These account for all 8 possible edge movements.

4. 4-swap of edges, type 3; vertical 4H order 2 type 2 [p168] (UF,UR)(DF,DR)(UB,UL)(DB,DL)
   Rs2 Fs2 U Rs2 D2 Fs2 U (11f*)
   Ls Ds R F2 L' Us Ls U R2 U' (16q*)
5. 4-swap of edges, type 4; 2X + vertical 4H order 2 type 2 [p162] (UF,DR)(DF,UR)(UB,DL)(DB,UL)
   U Fs2 Ua' Fs2 D (8f*,12q*)
   (U F2 D)⁴

Two opposite middle layer edge pieces could theoretically be swapped within this symmetry, but there is no other odd permutation to combine it with, so all 4 middle edges must be swapped at the same time, as seen before in 5i. The can be flipped in separate pairs however.

6. 2-flip of edges type 1, {FR+,BL+}
   F' R U' F R' Um2 R F' U R' F Um2 (14f*)
   R' B' R' B' R B2 R2 B' F' U' B U F R' (14f*,16q*)

These patterns (together with those in section 5) form a group of order 2048 (isomorphic to C₂¹¹), of which 128 were seen in section 5. The nice patterns are of two different types. This first few use only opposing colours on each face, and must use 9a on the corners.

7. 4a + 2X (9a+5f)
   F2 U2 Ra B2 D2 R2 F2 D2 Ra' (11f*)
   (F2 L2 U2)² R2 B2 D2 (F2 R2)²
8. 4T (9a+5g)
   L2 B' L2 Us2 R2 F' R2 (8f*)
   Ra D2 Fa D2 Fa' Ra' U2 (14q*)
   R2 (F2 U2)³ R2 U2 F2 R2 F2 D2
9. 4T + 2X [p135] (9a+5h)
   Ra' Fa D2 Ra2 Fa' U2 Ra' U2 (13f*)
   (U2 F2 R2)² D2 R2 F2 U2 (F2 R2)² U2 (antipode in square group)
10. 4c [p78] (9a+5i)
    R2 F Rs2 F2 Rs2 F' R2 (9f*)
    U2 B2 L2 B2 U2 L2 (U2 F2)³ L2
    (F2 R2 U2)² R2 F2 U2 (F2 L2)²
11. 4c + 2X (9a+5f+5i)
    B2 U2 Ra B2 U2 R2 F2 D2 Ra' (11f*)
    (F2 R2 U2)² L2 B2 D2 (F2 R2)²
12. 4D (9a+5g+5i)
    Ra D2 Fa' U2 Fa Ra' U2 (11f*)
    R2 (B2 U2)³ R2 U2 F2 R2 F2 D2
13. 4D + 2X [p137] (9a+1a)
    Fs2 R2 F L2 Us2 R2 B R2 (10f*)
    (L2 B2 U2)² B2 R2 Fs2 U2 (R2 F2)² (antipode in square group)

The remaining nice patterns show adjacent colours on the sides, all except the first use 9c and/or 9b' on the corners.

14. 4K (9d+9f)
    L D B' U' F' L' B F2 L2 F R F L U' F' R' (16f*,18q*)
15. 6+ of order 2, Christman Cross [p14, p113, RCC 3.9.33] (9b'+9c)
    U F2 U2 Rs F2 U2 F2 Rs' U (11f*, 16q*)
    U Fa Ra2 Fa Ua Fa2 D
16. 2 Deuce + 4T type 1 (9b'+9d)
    D' B2 D2 Rs2 D Fs2 Rs2 U' F2 U' (13f*)
17. 2 Deuce + 4T type 2 (9c+9d)
    D U2 B2 U' Rs Us2 Rs' U' F2 U' (13f*,18q*)
18. 2+ + horizontal 4I (9b'+9c+9d)
    B2 D2 L2 B2 Us' R2 F2 U2 R2 (10f*)
19. 4T + 2 diagonals, type 1 (9b'+9e)
    D' F2 R2 F2 L2 Ua' L2 F2 R2 F2 U' (12f*)
20. 4T + 2 diagonals, type 2 [p161] (9c+9e)
    U' Fa' L2 Fa U2 Ra F2 Ra' U' (13f*,16q*)
    (U Ra D)³ (Um2 B2)²
21. Horizontal 4I + 2O (9b'+9c+9e)
    Fa Ra2 Fa' Us (8f*,10q*)
22. 2 Diagonal + 4a (9b'+9d+9e)
    D' F2 U' Rs2 Us Rs2 U' F2 U' (12f*)
23. 2 Diagonal + 4a (9c+9d+9e)
    D Ra2 D2 Fa L' Fs2 Us2 R' Fa' U' (15f*)
24. 2O + 4+ (9b'+9c+9d+9e)
    Rs Us2 Rs' D L2 U2 Fs2 U2 R2 U' (14f*)
25. 4Y + 2 deuce (9b'+9f)
    D2 B2 U B2 D' R2 B2 D' R2 F D R' B2 R D' F' U' (17f*)
26. 2 flipped columns (9c+9f)
    F2 L2 F' R F2 L' U L2 U' L F2 R' F' (13f*)
27. 4t + 2+ (9b'+9c+9f)
    D L2 F2 Us R Us' B L2 B' Us L2 R' U' (16f*)
28. 4V + 2 deuce (9b'+9d+9f)
    U' B2 D L2 B2 L2 U2 B2 F U' F L2 R U2 B' U B' R' (18f*)
29. 4ct + 2 deuce (9c+9d+9f)
    B2 R' D' L2 U2 F2 R' U' R' U2 B F2 L2 B' R U L2 R' (18f*)
30. 4U + 2+ (9b'+9c+9d+9f)
    R2 F2 Rs2 Us L' Fs U' F2 D2 U' Fs R' (16f*)
31. 4K + 2X (9e+9f)
    U' R2 U2 B2 D2 R2 D2 R Us F' L2 F Us' R' U' (17f*)
32. 4V + 2 diagonals [p93] (9b'+9e+9f)
    D F2 U F2 R2 F2 D' L B' D' Fs2 U B R U' (16f*)
33. 4ct + 2 diagonals (9c+9e+9f)
    D F2 U' R2 B2 R2 D R' F D Rs2 U' B' R' U' (16f*)
34. 4U + 2O (9b'+9c+9e+9f)
    L2 B2 Us L' Fs D2 U B2 U Fs R' (14f*)
35. 4A + 2X (9d+9e+9f)
    Ua B2 Us' R2 B2 R Us F' L2 F Us' R' U2 (17f*)
36. 4Y + 2 diagonals (9b'+9d+9e+9f)
    D2 B2 U L2 U' F2 R2 L F' D F2 D' F L F2 U' F2 U' (18f*)
37. 4 rectangles + 2 diagonals (9c+9d+9e+9f)
    B2 L2 F2 L2 R' U F2 U' F L2 F' U F2 U' R' (15f*)
38. 4t + 2O (9b'+9c+9d+9e+9f)
    U L2 D' Rs2 B2 D F2 L U' B U2 B' U L' F2 U' R2 (18f*)

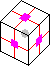
10. Symmetry m_fr2_er2_e, <(13), (24), (12)(34)>, 8.

Suppose the r2 symmetries are again centred around the middle layer edges, but that now a plane of reflectional m symmetry goes through a vertical slice.

The corners are no longer in two orbits but in a single one, so now the movement of one corner determines the movement of all the other corners. There are two ways the corners can move that were not in section 5, both of which can be used in two orientations:

1. 4-swap of corners, type 5 (URF,UBR)(UFL,ULB)(DFR,DLF)(DBL,DRB)
   L2 U2 B2 R2 D2 F2 L2 D Rs2 Fs2 U' F2 (14f*)
2. Two 4-cycles of corners, type 2 [p66] (URF,DLF,ULB,DRB)(ULF,DFR,UBR,DBL)
   U2 R2 B2 U2 R2 Fa' D2 L2 Us2 Fa (13f*)
   B2 U2 (R2 B2)² (L2 F2 U2)² B2 L2 F2 (antipode in square group)

Note that applying 10b twice gives the 4-swap 5a.

The corners can also be twisted:

3. 8-twist [p155] {URF+,UFL-,ULB+,UBR-,DRB-,DFR+,DLF-,DBL+}
   F2 Ra B2 U' L2 D2 L' B2 Ua F2 L' U2 R2 U' (16f*)

Note that 10a/b and 10c do not commute (e.g. 10a+10c is not equal to 10c+10a), and this is the first occasion we have seen where the corner twists do not commute with corner permutations.

The edges in the middle layer can only move and flip in the same way as in section 5. There is a vertical plane of symmetry through each of the U/D edges, so these edges cannot leave their slice without breaking the symmetry. They occur in two orbits, {UF,UB,DL,DR} and {UL,UR,DF,DB}. An orbit can only move as follows:

4. 2-swap of edges, type 1 (UR,UL)(DF,DB)
   (U Rm2 U)² (7f*,12q*)
   (F2 U2)² F2 R2 F2 U2 L2 D2 B2 L2

These two edge orbits can be swapped by 5f. Furthermore, they can be flipped separately:

5. 4-flip of edges {UR,UL,DF,DB}
   L' U R2 B' L2 D Ra D' L2 F R2 U' R' (14f*)

The U/D edges can only be flipped together, as in section 5.

These patterns (together with those in section 5) form a group of order 3072 (=2¹⁰3, but the exact group structure is a bit too complicated to describe here), of which 128 were seen in section 5.

6. 2O, 4a (10b+5f)
   D U2 R2 F2 Us2 F2 R2 U' (9f*)
   (L2 U2)³ F2 R2 U2 F2 U2 L2 B2
7. 2+, 4T [p118] (10b+5i)
   U2 F2 R2 U2 F2 Ra U2 F2 Ra3 (11f*)
   (U2 R2)² U2 L2 B2 R2 D2 F2 D2 L2 D2
8. 2O, 4T [p80] (10b+5f+5i)
   U L2 Fs2 Us2 L2 U2 D' (9f*)
   (R2 F2)² (U2 F2)² U2 R2 B2 U2 R2 U2 L2 (antipode in square group)
9. 2+, 4 rectangles (10b+10d')
   Rs2 U2 F2 Rs2 Us2 B2 (9f*)
10. 2O, 4 rectangles (10b+10d'+5f)
    D2 Ra Fa2 Ra' (7f*,10q*)
    R2 Fs2 L2 Fs2 U2 B2 Us2 B2
11. 2+, 4ct (10b+10d'+5i)
    B2 D2 R2 Fs2 R2 U2 F2 U2 (9f*)
    Fs2 U2 R2 F2 Us2 F2 L2
12. 2O, 4ct (10b+10d'+5f+5i)
    F2 U2 Rs' B2 U2 B2 Rs' (9f*)
    Rs2 U2 F2 Rs2 Us2 F2 Rs2
13. 2+, 4Y (10b+10d)
    B2 Us2 Rs2 F2 U2 Rs2 (9f*)
14. 2O, 4Y (10b+10d+5f)
    Fs2 U2 F2 R2 Us2 R2 B2 (9f*)
15. 2+, 4V (10b+10d+5i)
    R2 F2 Us2 F2 L2 D2 Fs2 (9f*)
16. 2O, 4V (10b+10d+5f+5i)
    B2 Rs2 U2 Fs2 U2 F2 U2 (9f*)
17. 2+, 4c [p100] (10b+10d+10d')
    R2 Us2 R2 Fs2 U R2 Fs2 L2 D (12f*)
    (F2 R2)² (U2 L2)² D2 F2 R2 (U2 F2)² (R2 F2)² (antipode in square group)
18. 2O, 4c (10b+10d+10d'+5f)
    D' F2 R2 Us2 R2 F2 U' (8f*)
    (F2 U2)² (F2 U2 R2)² D2 F2 R2
19. 2+, 4D (10b+10d+10d'+5i)
    U2 F2 L2 D2 F2 Ra D2 F2 Ra' (11f*)
    (U2 F2)² U2 B2 R2 F2 U2 R2 D2 F2 L2
20. 2O, 4D [p99] (10b+10d+10d'+5f+5i = 10b+1a)
    U F2 Rs2 Us2 F2 D (8f*)
    (F2 R2)² (D2 R2)² U2 B2 R2 (U2 F2)² (antipode in square group)

21. 2X, 4A (10d+5f)
    Fa D2 Fa Ra' D2 Ra' (10f*,12q*)
    (R2 U2)² L2 B2 R2 U2 F2 U2 R2 Us2 B2
22. 4K [p188] (10d+5i)
    D' Fs2 Ua' Rs2 U' (8f*,12q*)
    (U Ra U)⁴
    R2 U2 R2 F2 D2 R2 F2 L2 D2 F2 U2 L2
23. 2X, 4K (10d+5f+5i)
    Fs2 Rs2 U' Fs2 U2 Fs2 U' (11f*)
    (R2 U2)² L2 F2 L2 D2 F2 U2 R2 F2
24. 4t (5a+10d)
    U' Fs2 U2 Fs2 U' (7f*,12q*)
    (R2 U2)² R2 F2 R2 D2 F2 D2 R2 F2
25. 2X, 4t (5a+10d+5f)
    Fs2 Rs2 D' Fs2 Ua' Rs2 U' (12f*)
    L2 D2 F2 D2 L2 F2 L2 U2 F2 R2 U2 R2
26. 4U of order 2 type 1 [p57] (5a+10d+5i)
    U Fa Ua2 Fa' U' (8f*,10q*)
    (R2 U2)² Fs2 L2 F2 L2 D2 B2 U2 L2 F2
27. 2X, 4U (5a+10d+5f+5i)
    B2 L2 U2 B2 Ra U2 F2 Ra' (10f*)
    (F2 U2)² B2 L2 B2 U2 R2 U2 B2 R2

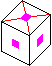
11. Symmetry m_fr2_fr2_f, <(12)(34), (14)(23), i>, 8.

Suppose the r2 symmetries are centred around the faces, and that a plane of reflectional m symmetry goes through the middle layer. Note that the point reflection m_c also lies in this group, as do m_f through the vertical slices.

The corners lie in a single orbit, so the movement of one determines the movement of the others, and there are therefore (at most) eight possible corner positions. These are generated by the 5a-b and the following:

1. 4-swap of corners, type 6 (URF,UBR)(UFL,ULB)(DFR,DRB)(DLF,DBL)
   F2 U' F2 U2 F2 Ra (F2 U2)² Ra' U' F2 (15f*)

They can be twisted only by the supertwist 3a.

There is a plane of symmetry through each slice, so none of the edges can move from their slices. They can swap with their opposites using 5i (in any orientation) or the following double swap:

2. 2H pattern; 2-swap of edges, type 2 [p21, RCC 3.9.4] (UF,DF)(UB,DB)
   (Rm2 F2)² (6f*,12q*)
   D2 Rs Fs2 Rs' U2

By using this in different orientations all 4 allowed positions of the edges in a slice can be achieved. The slices can also be flipped separately (use 5d in a different orientation).

These patterns form a group of order 12288 (isomorphic to C₂³C₃×C₂⁹).

All patterns which twist or move the corners relative to each other in any way or flip any edges will have more than 2 colours on some faces. Therefore the nice patterns are much more limited than the group size suggests. Here are all patterns (other than 3b, 11b and those in section 5) that don't move the corners:

3. 2H + 4X [p32]
   Us2 R2 Fs2 R2 (6f*,12q*)
4. 6H, type 2 [p174]
   D2 Fs' Us2 Fs' U2 (8f*,12q*)
   U2 (R2 Fs2)² U2 Fs2
5. Vertical 2H, horizontal 2H
   R2 Ua Fa2 Ua L2 (8f*,12q*)
   F2 R2 (Fs2 U2)² R2 B2
6. 2X, vertical 2H, horizontal 2H
   R2 U2 Fs2 U2 L2 (6f*,12q*)
7. 2X, horizontal 2H
   Fa' Ua2 Fa Ua2 (8f*,12q*)
   Fs2 U2 F2 R2 Fs2 R2 F2 U2
8. 2X, vertical 2H
   F2 R2 Fs2 R2 Us2 F2 (8f*)

All nice patterns where the corners do move can be made by doing one of the nice patterns above (or of section 5) and then turning one pair of opposite faces 180 degrees.

9. 2I, 2O, type 1 (11b'+Us2)
   R2 Um2 R2 (4f*,8q*)
10. 2H + 2I + 2O; Ohio type 1 (11e+Rs2)
    U2 Ra Fa2 Ra U2 (8f*,12q*)
    F2 R2 Us2 R2 F2 Rs2
11. Horizontal 2I, vertical 2I [p23a] (5j+Fs2)
    R2 U2 Rs2 U2 R2 (6f*,12q*)
12. 2H, horizontal 2I, vertical 2I, type 1 (11g+Rs2)
    Ra Fs2 Ra (6f*,8q*)
    F2 R2 U2 Rs2 U2 R2 B2
13. 2H + 2I + 2O; Ohio type 2 (5g+Rs2)
    Ra' Fa Ra2 Fa Ra (12q*)
    Fs2 R2 Fs2 Us2 R2 (8f*)
14. 2X, 2I, 2O, type 1 (11h+Fs2)
    D2 F2 Us2 F2 Rs2 U2 (8f*)
15. 2H, horizontal 2I, vertical 2I, type 2 (11h+Rs2)
    D2 B2 Rs2 Us2 F2 U2 (8f*)
16. 2X, horizontal 2I, vertical 2I [p34] (5o+Fs2)
    F2 Ua Fs2 Ua F2 (8f*,12q*)
    U2 L2 Us2 L2 U2 Fs2 (8f*)
17. 2+, 2O [p30] (11e+Us2)
    R2 Fs' Rs2 Fs L2 (8f*,12q*)
    R2 U2 Fs2 U2 R2 Fs2 (8f*)
18. 2H, 2+, 2O, type 1 (3b+Rs2)
    Ua Fa Ua2 Ra2 Fa Ua
    D2 L2 F2 Us2 F2 R2 U2 (8f*)
19. 2+, vertical 2I [p203] (11h+Us2)
    B2 R2 Us Rs2 Us' R2 F2 (10f*)
    F2 R2 Fs2 R2 Us2 F2 Us2
    R2 D2 (Fs2 R2)² D2 R2
20. 2H + 2I + 2+, type 1 (11f+Rs2)
    R2 Us Rs2 Us' R2 (8f*,12q*)
21. 2H, 2+, 2O, type 2 [p24] (11d+Rs2)
    Fa D2 Rs2 U2 Fa (8f*,12q*)
    Fs' D2 Rs2 U2 Fs (8f*,12q*)
    R2 Fs2 U2 Fs2 U2 L2 (8f*)
22. 2X, 2+, 2O [p33] (11f+Us2)
    Us2 B2 U2 Rs2 U2 F2 (8f*)
23. 2H, 2I, 2+, type 2 (5l+Rs2)
    Us2 B2 Rs2 Us2 F2 (8f*)
24. 2X, 2I, 2+, type 1 (11c+Fs2)
    (Us2 F2)² Rs2 (8f*)
25. 2H + horizontal 4I (11b+Us2)
    F2 Rs2 B2 Rs2 Us2 (8f*)
26. 2+, horizontal 2I (11b+Fs2)
    (Rs2 U2)² (6f*,12q*)
27. 2H, 2I, 2+, type 3 (5i+Rs2)
    Rs Fs2 Rs' (6f*,8q*)
    F2 Rs2 B2 U2 Rs2 U2
28. 2H, 2I, 2+, type 4 (11e+Fs2)
    Us2 B2 Ra Us2 Ra F2 (10f*)
    (Fs2 R2)² U2 Rs2 U2 (10f*)
29. 2X, 2I, 2+, type 2 (11g+Fs2)
    (Rs2 Ua)² (8f*,12q*)
    R2 U2 F2 Us2 F2 U2 R2
30. 2H, 4+ (11d+Fs2)
    R2 (F2 Us2)² R2 (8f*)
31. 2H, 4O [p71] (11d+Us2)
    D2 Fs Us2 Fs D2 (8f*,12q*)
    Fs2 D2 (R2 Fs2)² U2
32. 2I, 2O, type 2 [p22, RCC 3.9.12] (11g+Us2)
    Fa Ua2 Fa' (6f*,8q*)
    Fs2 U2 F2 R2 Fs2 R2 F2 D2
33. 2H + 2I + 2O; Ohio type 3 (5p+Fs2)
    Fs Us2 Fs (6f*,8q*)
    U2 Fs2 D2 Fs2 R2 Fs2 R2
34. 2H + 2I + 2O; Ohio type 4 (5f+Rs2)
    U2 F2 Rs2 F2 U2 (6f*,12q*)
35. 2X, 2I, 2O, type 2 [p11] (11c+Rs2)
    Rs2 D2 Fs2 U2 (6f*,12q*)
36. 2H + vertical 4I (11c+Us2)
    R2 Fs2 R2 (4f*,8q*)

Patterns with three colours on a face can be nice too:

37. Stripes [p92] (11a+5b+11b'+5d)
    F U F R L2 B D' R D2 L D' B R2 L F U F (17f*, 20q*)

12. Symmetry m_er2_fr2_f, <(12)(34), (14)(23), (13)>, 8.

Suppose the r2 symmetries are again centred around the faces, and that now a plane of reflectional m symmetry goes through the U/D axis and four corners, i.e. diagonally through the U/D faces.

The corners occur in two orbits, of which URF,ULB,DFL,DBR form one. Each set can be moved in only one way:

1. 2-swap of corners, type 4; 4-deuce [p76] (URF,ULB)(DFL,DBR)
   D2 U' L2 B' L2 Us2 R2 F' R2 U' (11f*)
   L2 D2 B2 D2 B2 R2 B2 L2 (U2 F2)² R2 F2

The two corner orbits can also be swapped by 5b-c (the corner permutation group is then isomorphic to D₄). The corners cannot be twisted.

The movement of one U/D edge determines the movement of all the others, so there are only eight possible U/D edge positions. These are generated by the 5f-h and the following:

2. Two 4-cycles of edges, type 2 (UF,DL,UB,DR)(DF,UR,DB,UL)
   Rs2 U Rs2 Fs2 U' Fs2 (10f*)
   U Fa D2 Fa Ra' D2 Ra' U' (14q*)

Note that applying it twice has the same effect as 5g. As before these 8 edges can only be flipped all at once. The middle layer edges only move the same as in section 5.

These patterns form a group of order 512 (isomorphic to D₄²×C₂³).

Patterns using 12b or edge flips always have at least 2 colours on some faces so generally do not make nice patterns. To be a new pattern, it must therefore use 12a in one orientation only. This leaves only the following:

3. Vertical 4S pattern [p64a, RCC 3.9.11] (12a+5i)
   U R2 F Rs2 F2 Rs2 F' R2 U' (11f*)
   Ra Fa' Ra Fa Ra' Fa (12q*)
   (R2 F2)² U2 L2 U2 (R2 F2)² D2 R2 D2
4. Horizontal 4S pattern (12a+5g)
   U L2 B' L2 Us2 R2 F' R2 U' (10f*)
   (R2 F2)² U2 L2 U2 (R2 F2)² D2 R2 U2
5. 4 diagonals [p17/61, RCC 3.9.10] (12a+5g+5i)
   (Fa Ra)³ (12f*,12q*)
   (F2 U2)² R2 U2 L2 B2 U2 F2 (U2 R2)²
6. 2X + 4-deuce [p198] (12a+5f)
   Ra Fa Ra' Fa' Ra Fa (12f*,12q*)
   (F2 U2)² R2 D2 R2 B2 D2 B2 (U2 L2)²
7. 2X + vertical 4S pattern (12a+5f+5i)
   F2 R2 Ua R2 B2 L2 F2 Ua F2 R2 (12f*)
   B2 (D2 R2)² B2 L2 B2 (D2 L2)² F2 L2
8. 2X + horizontal 4S pattern (12a+5h)
   Fa' Ra Fa Ra Fa Ra' (12f*,12q*)
   (R2 B2)² (U2 L2)² F2 R2 B2 D2 L2 U2
9. 2X + 4 diagonals [p65] (12a+5h+5i)
   F2 R2 Ua' L2 B2 L2 B2 Ua' F2 R2 (12f*)
   (B2 U2)² L2 D2 R2 B2 D2 F2 (U2 R2)²

13. Symmetry m_cr4, <(1234), i>, 8.

We can hold the cube so that the r4 symmetry is around the U-D axis. Note that reflection m_f through the middle layer also lies in this symmetry group.

The movement of one corner determines the movements of the others, so there are eight possibilities. These are generated by 5b and this double 4-cycle:

1. 4+ pattern of order 4 [p15, RCC 3.9.15] (URF,UFL,ULB,UBR)(DFR,DLF,DBL,DRB)
   (Fm2 U2 Rs2 U)² U2 (12f*)
   (Rm2 D Rm2 U')³
   (Rs2 U Rs2 U')³

The corners can be twisted if the U corners all twist in the opposite direction to the D corners.

2. 8-twist {URF-,UFL-,ULB-,UBR-,DRB+,DFR+,DLF+,DBL+}
   D' L2 F D2 F2 U L2 Fa' R2 U B2 U2 F R2 U' (16f*)

Note that this commutes with 13a, but not with 5b (and the corner group is thus isomorphic to C₄×D₃). The U/D edges move in the same way as the corners, in the movements generated by 5f and this double 4-cycle:

3. 4H pattern of order 4 [p19, RCC 3.9.16] (UF,UL,UB,UR)(DF,DL,DB,DR)
   Rs2 D2 Fs2 D Fs2 D2 Rs2 D' (12f*)

These can all be flipped. The middle layer edges could do a 4-cycle in this symmetry, but this is an odd permutation and there is no other odd permutation possible. Therefore they can only move as before (5i) and be flipped (5d).

These patterns form a group of order 1536 (isomorphic to C₄²×D₃×C₂⁴).

4. Horizontal 4I pattern of order 4 (13a+13c)
   Us (2f*,2q*)
5. 2X + horizontal 4I pattern of order 4 (13a+13c+5f)
   U2 Fs2 Us' Fs2 U2 (8f*)
6. 4+, 2X (13a+5f)
   U' L2 U2 R2 F2 Ua' F2 L2 U2 R2 U' (12f*)
7. 4H, 2X (13c+5f)
   U Fa' D2 Fa' Ra' U2 Ra' U' (12f*,14q*)

8. 4a, 2+ (13a+5b)
   Fs2 Ra' Fa' D2 Fa' U2 Ra' U2 (13f*)
   (B2 R2)² U2 L2 B2 D2 F2 Us2 L2 U2 B2 L2 (antipode in the square group)
9. 4a, 2O (13a+5b+5f)
   B2 L2 Ua B2 R2 Ua' F2 R2 U2 (11f*)
   F2 R2 F2 U2 R2 F2 D2 (F2 U2)² R2 U2
10. 4T, 2+ (13a+5b+5g)
    B2 U2 Ra F2 D2 L2 F2 D2 Ra' (11f*)
    (F2 R2)² D2 R2 F2 (U2 F2 R2)²
11. 4T, 2O [p109] (13a+5b+5h)
    F2 L2 Ua F2 R2 Ua' B2 R2 U2 (11f*)
    (R2 F2)² U2 B2 R2 (U2 L2 F2)²
12. 4c, 2+ p[140] (13a+5b+5i)
    Fs2 Ra' Fa U2 Fa U2 Ra' U2 (13f*)
    (R2 B2)² U2 Rs2 F2 L2 (U2 R2 F2)² (antipode in square group)
13. 4c, 2O (13a+5b+5i+5f)
    B2 L2 Ua' F2 L2 Ua F2 R2 U2 (11f*)
    F2 (R2 U2)² R2 D2 B2 U2 L2 F2 R2 U2
14. 4D, 2+ (13a+5b+5i+5g)
    F2 U2 Ra F2 U2 L2 F2 D2 Ra' (11f*)
    (F2 R2)² D2 R2 B2 (U2 B2 R2)²
15. 4D, 2O (13a+5b+5i+5h)
    F2 L2 Ua' B2 L2 Ua B2 R2 U2 (11f*)
    (R2 F2)² U2 B2 L2 (U2 R2 F2)²

14. Symmetry m_er4, <(1234), (13)>, 8.

Again we can hold the cube so that the r4 symmetry is around the U-D axis. This time the plane of reflectional symmetry is vertical, through the U-D axis (can be either m_e or m_f since if one lies in the group then so do all the others).

The U-corners form one orbit, but due to the reflection they cannot move in a 4-cycle, nor can they be twisted. The only remaining possibility is swapping diagonally:

1. 2-swap of corners type 5 [RCC 3.9.1] (URF,ULB)(UFL,UBR)
   (F2 Rm2 F2 U)²
   L2 Fs2 R2 D' L2 Fs2 R2 U' (10f*)
   (U2 F2 R2)² (F2 R2)² U2 R2 F2

The same goes for the D-corners. The two orbits can be swapped only by the sequences 5b and 5c. (This leads to a corner permutation group isomorphic to the dihedral group D₄.)

The U/D edges also cannot move in 4-cycles, but can be swapped with the opposites in the same layer, by 5g or by:

2. 2-swap of edges type 3 [p52, RCC 3.9.2] (UR,UL)(UF,UB)
   (F2 Rm2 F2 U)² U2
   Ra U2 Ra' Fa' U2 Fa (10f*,12q*)
   F2 R2 U2 (F2 R2)² U2 R2 F2

They can also be flipped by 5d and:

3. 4-flip of edges type 2 [p182, p192, RCC 3.2.3] {UF+,UL+,UB+,UR+}
   Rs2 B2 Rs' U2 B' U2 Rs B2 Rs2 U (14f*)
   (Fa U Ra)⁶

The U and D layer edges can also be swapped by the sequence 5f. The middle layer edges move the same as in section 5.

These patterns therefore form a group of order 1024 (isomorphic to D₄C₂²xD₄×C₂²). Below are all the nice patterns.

4. U2 (14a+14b)
   U2 (1f*,2q*)
5. 4T [RCC 3.9.9] (14a+5i)
   D' B2 Rs2 F2 U' L2 Fs2 R2 (10f*)
   F2 (U2 F2 R2)² F2 D2 L2 D2 F2 U2
6. 4K (14b+5i)
   D' B2 Rs2 F2 U' L2 Fs2 R2 U2 (11f*)
   F2 (U2 F2 R2)² F2 D2 L2 D2 F2
7. 4Y (14a'+14b)
   R2 Fs U2 R2 U2 Fs' R2 (9f*)
8. 4t (14a+14a'+14b)
   D' L2 Fs2 R2 U' L2 Fs2 R2 U2 (11f*)
   (F2 D2)² F2 R2 B2 D2 R2 U2 F2 L2
9. 4ct (14a+14b+5i)
   D' Fs2 Us' Rs2 U' (8f*,12q*)
   F2 Us2 R2 Us2 L2 F2 U2
10. 4V (14a+14b'+5i)
    R2 F2 Rs2 F2 L2 D2 (7f*)
11. 4U of order 2 type 2 [p58 RCC 3.9.8] (14a+14a'+14b'+5i)
    Ra' U2 Ra Fa' U2 Fa (10f*,12q*)
    (R2 U2)² F2 (B2 L2)² D2 B2 D2 R2 F2
12. 4c (14a+14b+14b')
    F2 R2 U2 B2 Ra' U2 F2 Ra' U2 (11f*)
    (U2 F2 R2)² (B2 R2)² D2 L2 B2
13. 4D (14a+14b+14b'+5i)
    B2 Rs2 F2 D U2 L2 Fs2 R2 U' (11f*)
    L2 U2 B2 U2 R2 B2 R2 D2 F2 (R2 U2)² (11f*)
14. 4a + 2X (14a+5f)
    Fa' D2 Fa' Ra' U2 Ra' U2 (11f*)
    L2 (U2 R2 F2)² L2 U2 B2 D2 R2 D2
15. 4A + 2X [p59] (14b+5f)
    Fa' U2 Fa' Ra' D2 Ra' (10f*,12q*)
    (F2 D2)² L2 (R2 F2)² U2 R2 D2 F2 L2
16. U2 + 2X (14a+14b+5f)
    Ua Rs2 Us' Rs2 (8f*,12q*)
    F2 Us2 F2 R2 Us2 R2 D2
17. 4T + 2X (14a+5i+5f)
    Fa' U2 Fa' U2 Ra' U2 Ra' (11f*)
    (D2 F2 R2)² (F2 L2)² D2 L2 B2
18. 4K + 2X [p55] (14b+5i+5f)
    Fs2 U' Rs2 U2 Rs2 U' Rs2 (11f*)
    (R2 D2)² L2 F2 R2 D2 F2 D2 R2 B2
19. 4Y + 2X (14a'+14b+5f)
    Rs2 Us' Rs2 Ua' (8f*,12q*)
    R2 Us2 R2 F2 Us2 F2 U2
20. 4t + 2X (14a+14a'+14b+5f)
    L2 U2 L2 F2 Ua' F2 R2 U2 R2 Ua' (12f*)
    L2 (D2 R2 F2)² R2 U2 F2 D2 L2
21. 4ct + 2X (14a+14b+5i+5f)
    D2 Fs2 Rs2 (5f*,10q*)
22. 4V + 2X (14a+14b'+5i+5f)
    Fs2 Rs2 D2 (5f*,10q*)
23. 4U + 2X (14a+14a'+14b'+5i+5f)
    F2 R2 D2 F2 Ra U2 F2 Ra' (10f*)
    L2 (U2 R2 F2)² R2 U2 B2 D2 L2
24. 4c + 2X (14a+14b+14b'+5f)
    Fa' U2 Fa' Ra' D2 Ra' U2 (11f*)
    L2 (D2 R2 F2)² R2 U2 F2 D2 L2 D2
25. 4D + 2X (14a+14b+14b'+5i+5f)
    F2 Ua' L2 B2 D2 L2 B2 Ua' R2 (11f*)
    B2 L2 U2 B2 U2 L2 F2 U2 (R2 D2)² L2 (11f*)

15. Symmetry m_cr3, <(123), i>, 6.

Suppose the reflection is through the centre of the cube. First consider the corners. The corners on the r3 axis cannot move (if they were swapped their orientation would spoil the r3 symmetry), but can be twisted in opposite directions.

1. 2-twist of corners UFR-,DLB+
   (L' F2 L U' B2 U)² (12f*)
   F' L' U' L D L' U L F U F' D' F U' (14q*)

The other six corners can move in two 3-cycles around the axis.

2. Two 3-cycles of corners, type 1 (URB,FUL,RFD)(DRB,BUL,LFD)
   U F' R F R' B' U R F' R' F U' B U' (14f*, 14q*)

Each corner can also be swapped with its opposite, but this is an odd permutation so cannot be done without moving edges too. These six corners can also be twisted, 3 one way and 3 the other.

3. 6-twist of corners, type 1 {UBR-,FUL-,RFD-,DRB+,BUL+,LFD+}
   R2 F2 U' F2 R2 F' R' F' U R' B U' B' F R2 F' R' F2 (18f*)

The edges adjacent to the corners on the axis can also be cycled around, in two 3-cycles in opposite directions (when looking at their respective corners).

4. Two 3-cycles of edges, type 1 (UR,FU,RF)(DL,BD,LB)
   U' B D2 R' D2 B' U D' R U2 B U2 R' D (14f*,18q*)

Swapping these with their opposites is an odd permutation, but this can be combined with the corner swap mentioned above, and this is the same as 7a. Note that sequence 7a does not commute with the 6-twist 15c (in fact the sequences 15c and 7a generate a group isomorphic to the dihedral group D₃).

The ring of the other 6 edges can also move around in two 3-cycles.

5. Two 3-cycles of edges, type 2 (FL,RD,UB)(FD,RB,UL)
   F L B U L Fs2 R' Fs2 U' B' L' F' (14f*)
   D L' U R' B' R B U2 D B D' B' L Us (16q*)

These two orbits of six edges can also be interchanged by using the 6H pattern 3b in either of its two orientations, and flipped separately by 7b, and 7h. Note that 3b and 7b do not commute (and generate a group isomorphic to C₄).

These patterns form a group of order 7776 (= 2⁵3⁵, but its exact group structure is a bit too complicated to describe here), of which only 16 were seen in section 7.

This group has many nice patterns. There are two different types; a few with a pair of opposite colours on each face, and many with adjacent colours.

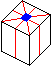
6. 6+ pattern order 3 a.k.a. Plummer's Cross [p101, RCC 3.9.28] (15a+15b)
   D2 U' R B2 D' R' Us Rs D R F2 D' L R2 (16f*, 20q*)
   F Ra2 Fa Ra2 F L Fa2 Ra Fa2 L Ua2
7. Tripod type 1 (15a+15d)
   F L F2 R F R' F2 L2 D F' L B R' B' D2 F' (16f*)
   B' L U' L' F U' B L2 B' L' U' F' U' F' U' Fs' (18q*)
8. Tips+ring turned (15a+15e)
   D U' R' U F' L' F D U' B D' B' L D' B R B' U (18f*,18q*)
9. Duck feet type 1 (15b+15d)
   F R' B R U F' L' F' U2 L' U' D2 B D' Fs U2 (17f*, 20q*)
10. Cube within a cube type 1 [p7, RCC 3.9.30] (15b+15e)
    U' L2 B D B' L U L2 F2 U' R' U F' L' F' (15f*, 18q*)
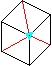
11. 6X of order 3. [p1, RCC 3.9.29] (15d+15e)
    R2 L' D F2 R' D' Fs Us F L D2 F' R L2 (16f*, 20q*)
    Us' L Us2 R2 Fs2 L F' Rs2 F2 Us2 F' Rs2 Us
12. Cube within cube within cube type 1, Twisted rings [p86] (15a+15b+15d)
    B R B' R2 U' F' L U R D L U' B' L U L2 (16f*,18q*)
13. Cube within cube within cube type 2 (15a+15b+15d')
    F' U B' R' U F2 U2 F' U' F U2 D B' D' R2 B2 U' (17f*)
    U' L' U' F' R2 B' R F U B2 U B' L U' F U R F' (20q*)
14. Anaconda [p121, RCC 3.9.31] (15a+15b+15e)
    F D R' D' Fs' R B' Rs' U B U' L' (14f*, 14q*)
15. Diagonal bands (15a+15d+15e)
    U R' U2 Fa R' D2 F2 D2 F2 L Ua' Fa U F' (17f*)
    R' F U' F' U B R' U' F U F' L Ds Fs' R' U (18q*)
16. Cherries / Chickenfeet, type 1 (15b+15d+15e)
    F L' D F' U' B U F U' F R' F2 L U' R' D2 (16f*, 18q*)
17. The 6-spot pattern [p202, RCC 3.9.25] (15a+15b+15d+15e)
    Rm Fm' Rm' Fm (8f*, 8q*)
    (Rm Uc)⁴
18. A 6A pattern (15d'+7b)
    U R2 B Rs' U' Ra' U' B' U' Fs' L F (15f*,16q*)
19. Small rectangles (15a+15d'+7b)
    U2 L2 D F R' F' D' F' R' B2 L' U R2 D2 F2 U' (16f*)
20. A 6F pattern (15b+15d'+7b)
    L2 F U' R F R' U L2 D R' U2 L' D B' D' L B' U2 (18f*)
21. A 6K pattern (15e+15d'+7b)
    D' L' B' D' B' U' L' D' U2 R B' F R B U F U (17f*,18q*)
22. A 6t pattern, type 1 (15a+15b+15d'+7b)
    Us2 L' F' R2 U' Rs2 F' L Fs2 D B2 L F Us2 (18f*)
23. (15a+15e+15d'+7b)
    L' D' B2 L (D2 B' L')² B R2 D' B' R' D L2 R U' (19f*)
24. (15b+15e+15d'+7b)
    B L Ua' F' U F D2 F2 D' B' D Fa R' U' (16f*,18q*)
25. A 6U pattern (15a+15b+15e+15d'+7b)
    F' R2 D' Rs F Ra F D B Ls U' F' (15f*,16q*)

25. A 6a pattern (15b+15c)
    D2 L2 Us' L2 F2 Us' F2 U2 (10f*)
    R2 F2 U2 (F2 R2)² U2 R2 F2
26. A 6c pattern [p200] (15b+15c+3b)
    Ua' B2 L2 Us R2 F2 U2 (9f*)
    U2 L2 F2 L2 U2 L2 D2 F2 U2 R2
27. A 6T pattern [p98] (15b+15c+3b')
    U2 R2 F2 Us B2 L2 Ua' (9f*, 14q*)
    F2 U2 R2 D2 B2 U2 B2 R2 B2 U2
28. A 6D pattern (15b+15c+1b)
    U2 L2 F2 Us' B2 L2 Ua' (9f*)
    R2 B2 U2 F2 L2 B2 R2 U2 L2 F2

29. 6X order 6 [p2] (15k+1a)
    F D R2 B' U' Rs Us' L2 R' B D2 L' F' Us2 (17f*)
    Rs2 U B L2 D' B2 F Rs Fs' R D F2 L' U'
30. 6-spot plus Pons [p197]
    Fs2 Rs' Fs Us Rs' (10f*,12q*)

16. Symmetry m_er3, <(123), (23)>, 6.

There is a plane of reflection through every corner. Because of this, they cannot be twisted, and the only remaining movement is that every corner except URF and BDL swpas with its opposite. This is an odd permutation, so it must be combined with an odd edge permutation, such as move 7a. The six edges that lie on the symmetry planes similarly can only swap with their opposites. In order to break the r2 symmetry the other six edges need to move, and they can do so either in two 3-cycles in opposite directions, or by three swaps (combined with an odd permutation of the other pieces).

1. Two 3-cycles of edges (FD,UL,RB)(FL,RD,UB)
   Ua R2 B Us2 L' Us2 R B' R2 Ua' (14f*)
2. 6 edge swaps (FD,LF)(UL,BU)(RB,DR) (FU,BD)(FR,BL)(UR,DL)
   D' B L2 U F2 L U2 B R2 U B2 L D' (13f*)

These patterns can be combined with the edge flips 1b, 7b, as well as the previously mentioned 7a. There are 48 patterns in this group, though only 16 have exactly this symmetry.

3. 16a+1b
   D' R2 F2 D2 B' D B' R' Fa L' F' U F' U2 B2 L2 U' (18f*)
4. 16a+7b
   R U' R D B D' L2 D2 L' Us2 Ra' Fs L' F' D' (18f*)
5. 16a+7b+1b
   L2 D' Rs2 F L D2 F' Rs' D B2 R' B' D L2 (16f*)
6. 16b+1b
   D F L2 D R' Fs2 Us2 L2 R' D' L2 F' D' (15f*)
7. 16b+7b
   B D' R2 F' U2 R' D F L U2 Fs2 U Fs' R D F U (19f*)
8. 16b+7b+1b
   Rs2 F' L' F' L B2 R' B D R D' Fa' R Us2 (17f*)
9. 16b+7a
   U Ra' B2 U' R2 B L2 D' F2 Ra' U' (13f*)
10. 16b+7a+1b
    B' U2 L' D B' L F U R2 B Ua R2 F' R' B2 D2 U (18f*)
11. 16b+7a+7b
    B' D R D B2 F Us' R' Fs' L2 B2 R2 D F2 L' U (18f*)
12. 16b+7a+1b+7b
    B' D R' Fs2 L2 U F L2 B' Rs U L U (15f*)
13. 16a+7a
    U R U2 Fa L' B2 D2 B2 R F2 R D2 F' D' (15f*)
14. 16a+7a+1b
    D F' D' L B D F D R B' U' Rs2 D Fa U (17f*)
15. 16a+7a+7b
    F2 U' B2 Us L2 U2 B U Rs' B' D Rs' U L' B R (19f*)
16. 16a+7a+1b+7b
    Rs2 F2 L2 U' Fs' L D' L D F D' B D' U2 (16f*)

None off the patterns above have only two colours per face. On larger cubes such patterns do exist, for example (UFr,UFl)(UfR,UbR)(uFR,dFR)(uFl,dFr)(Ufl,Ubr)(ubR,dfR), which looks like this.

17. Symmetry r3r2, S₃=<(123), (23)>, 6.

The r2 and r3 axes must be perpendicular (otherwise we get tetrahedral symmetry as handled in section 6), so the r2 axis goes through a pair of edges.

First consider the corners. The corners on the r3 axis cannot move (if they were swapped their orientation would spoil the r3 symmetry). They cannot be twisted because they would have to go in the same direction, and there is no way other corners can be twisted to compensate in this symmetry.

The other six corners can move in two 3-cycles around the axis, in the same direction.

1. Two 3-cycles of corners, type 2 (UFL,UBR,DFR)(ULB,DLF,DRB)
   U' R2 U' L' U Rs' D' L' U' L Ua R' U (15f*,16q*)

Each corner can also be swapped with its opposite, but this is an odd permutation so cannot be done without moving edges too. The corners can be twisted, all in the same direction.

2. 6-twist of corners, type 2 {UFL-,FRD-,RUB-,ULB-,FDL-,RBD-}
   U2 Ra' U R' U2 R' U Ra' U R' U' L2 U' R' U' (17f*)

The edges adjacent to the corners on the axis can also be cycled around, in two 3-cycles in the same direction.

3. Two 3-cycles of edges, type 3 (UF,RU,FR)(LD,BD,LB)
   Ua B2 L' F Us2 B' Us2 L B2 Ua' (14f*)

Swapping these with their opposites is an odd permutation, but this can be combined with the corner swap mentioned above, and this is the same as 7c.

The ring of the other 6 edges cannot move (except by swap with opposite by using 1a) because there is an axis of r2 rotation through each one. The two sets of 6 edges can be flipped separately, by 7b and 7h.

These patterns form a group of order 432 (isomorphic to D₃×C₄×C₃²×C₂).

The only nice patterns use opposing colours, but they do not lie in the square group:

4. 6a pattern (17a+17b')
   F2 R2 U2 R2 U R2 U' F2 U2 F2 R2 U F2 U (14f*)
   U B D F L' D2 U B' D U' B' U' L F U F' U' (18q*)
5. 6D pattern (17a+17b'+1a)
   F2 U' B2 L2 U' R2 U2 F2 U' F2 R2 D R2 U2 (14f*)

There is also one nice pattern (other than 17c) using adjacent colours:

6. 6A pattern of order 3 (17c+7b)
   L U Rs2 U' L U Rs' B' U' L' B Rs' U' (16f*,18q*)