Jaap's Puzzle Page

Rubik's Tangle

Rubik's Tangle

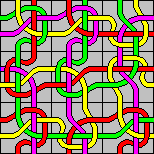
Rubik's Tangle is a tile puzzle. There are several variants of this puzzle, which all have very similar tiles. Each tile is square, and shows four ropes of different colours so that each rope connects two sides of the square, and each side has two ropes leading to it. All the tiles have the same rope pattern and uses the same four colours, though the colour arrangement usually differs. When laying tiles next to each other the ropes connect up, but you should only connect ropes of the same colour.

Rubik's Tangle, Original (5×5, one-sided):
The original version of Tangle was sold around 1990, has 25 cardboard tiles, and the aim was simply to make a 5×5 square with matching edges. The four rope pieces on a tile can be coloured in 4!=24 ways, and all these occur in a Tangle set. There is one duplicate piece to make the 25 tile set complete. The original Tangle came in four flavours, each with a different duplicate piece. An additional puzzle could be created by collecting all four sets, and trying to combine them into a 10×10 square. The four duplicate pieces are shown here:

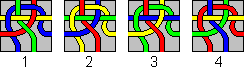
Tangle 1-4 Duplicate pieces

Another neat puzzle using any 5×5 tangle set is to use only the 24 unique tiles to cover the surface of a 2×2×2 cube.

Rubik's Mini Tangle (3×3, one-sided):
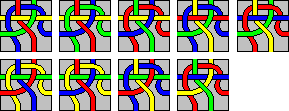
A simpler version of Tangle was also released around 1990 which was still made from cardboard but had only 9 tiles making a 3×3 square. The tiles are shown below. I believe it was used as a give-away item to promote the regular 5×5 tangle sets.

Mini Tangle tiles

Rubik's Tangle (3×3, double-sided):
The final version of Tangle came out in 1995. It is made of 9 plastic tiles, which have the rope pattern on both sides but with different colour arrangements. The aim is again of course to make a 3×3 square. The front and back of each tile is shown here:

Tangle tiles

The number of positions:

In the original tangle, there are 25 pieces, each with 4 possible orientations which gives 25!·425 = 1.75·1040 possible arrangements. Of course this number is a gross overestimate of the number of positions you would try out before finding all solutions since there is no point finishing an arrangement if the first few tiles you place already do not match. For comparison, the 10×10 Tangle has 100!·4100 / (4!20 5!4) = 1.8·10182 arrangements. The 3×3 Tangle on the other hand has a mere 9!·89 = 4.87·1013.

Links to other useful pages:

Patrick Hahn's page has further 10×10 tangle info here.
Raymond Penner's Site has similar information to this page.

Solution:

The four types of 5×5 tangles are all essentially the same, because we can get one from the other simply by swapping the rope colours around. Therefore their solutions are also exactly the same up to colour swaps. There are in fact two solutions, and you can see them all below. The duplicate tiles are shaded.

Tangle 1 Tangle 1 Solution A Tangle 1 Solution B
Tangle 2 Tangle 2 Solution A Tangle 2 Solution B
Tangle 3 Tangle 3 Solution A Tangle 3 Solution B
Tangle 4 Tangle 4 Solution A Tangle 4 Solution B

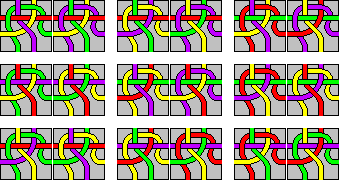
Sadly, the combined set of 100 tiles cannot be placed in a 10×10 square. The furthest you can get is 99 tiles, a square with one corner tile missing, and then you have one of the duplicate tiles left. Note how the pattern is built up from 2×2 squares which are repeated along broken diagonals. The four duplicate pieces don't quite make up the 2×2 square of which you would need 5 along the main diagonal in this type of pattern.

Near solution for 10x10 conbined tangle

Covering the surface of a 2×2×2 cube is possible, and the unique solution is shown here. Note how each face has exactly the same 2×2 pattern.

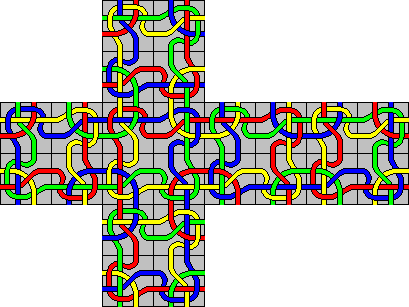
Solution for Tangle Cube

The original Mini Tangle (one-sided tiles, 3×3) has one solution shown below. It is interesting to note that it is actually the top left sub-square of the first Tangle 1 solution shown above.

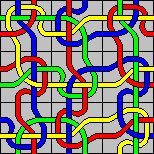
Mini Tangle Solution

The solution to the 3×3 tangle with double-sided tiles is shown here.

Tangle Solution