Introduction
Original Tantrix Puzzle (Crazy Tantrix)
About the background of this page
Tantrix Xtreme Puzzle
The Super 5 Puzzles
Three Pyramid Puzzles
The Rainbow Puzzles
The Discovery Puzzles
The "Unsolved" puzzles
My own puzzles
The Rock
Tips on solving a loop puzzle
Solutions to the Original Puzzle
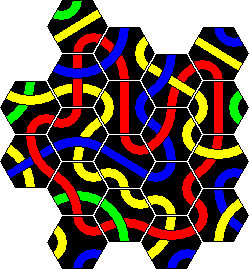
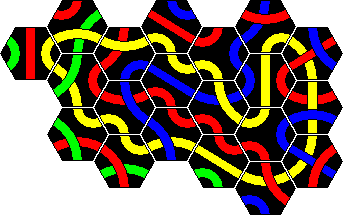
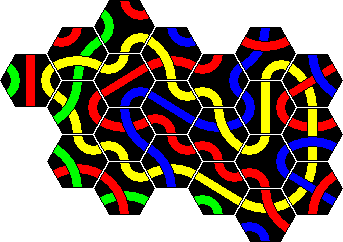
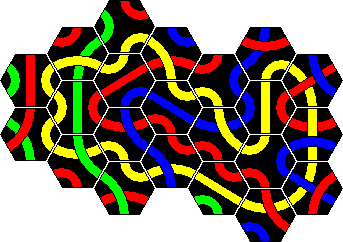
Solutions to Tantrix Xtreme
Solutions to the Super 5 puzzles
Solutions to the Pyramid Puzzles
Solutions to the Rainbow Puzzles
Solutions to the Discovery Puzzles
Solutions to the "Unsolved" puzzles
Solutions to my own puzzles
Solutions to the Rock
Tantrix is the brand name for a set of hexagonal Bakelite tiles. Each tile has three lines, of different colours, which go from one side to another. Some sets of tiles can be use as puzzles, in which you have to arrange the tiles so that the edges match in colour, thus forming coloured lines or even loops. The tiles can also be used for playing a game with two or more people. On this page however, I will only discuss the puzzles.
There are three kinds of line segments - straights, bends, and corners - and these lead to four different types of Tantrix tile:




The fifth possible tile shape, a tile with three straights, is not used in Tantrix.
The Tantrix game and puzzles were invented by Mike McManaway. The Tantrix tiles seem to be based on an older tile set, created some 40 years earlier by Charles Titus and Craige Schenstedt. It was marketed then as Psychepaths, but is now made and sold by Kadon Enterprises, Inc. with the name Kaliko. The Kaliko tiles form a complete set of all possible path patterns with 3 or fewer colours. Their patterns differ from Tantrix only in that a colour may be repeated on a tile, and the tile type with 3 straights is used as well.
There are and have been several different Tantrix tile sets available. There are various small sets, each containing about 10 distinct tiles, with which there are one or more puzzles to solve. There is however also a complete set of 56 tiles, and from that any of the small sets can be selected.
Each tile uses exactly 3 colours. There are 14 possible tiles with three colours: 2 with three corners, 3 with a straight and two corners, 3 with a straight and two bends, and 6 with a corner and two bends. The full set of tiles uses four colours (red, blue, green , yellow). Each tile is therefore missing exactly one of the four colours. This means that there are 4 sets of 14 tiles, for a total of 56 tiles.
I acquired the full set of 56 tiles quite a few years ago. At that time the numbering of the tiles was given in the accompanying booklet. Nowadays a different numbering scheme is used, and the numbers are engraved on the backs of the tiles and those numbers are painted in 5 different colours.
If we use the letters R, B, G, and Y for the path colours (red/blue/green/yellow), then the pattern on a tile can be described by a list of six such letters which denote the colour at each of the edges, going clockwise around the tile. Below are conversion tables for the two tile numberings, also listing all the tile patterns, and the colour of the number in the new numbering.
| Old | New | Colour |
|---|---|---|
| 37 | 1y | YYBRBR |
| 33 | 2y | RRBYYB |
| 29 | 3y | BBYYRR |
| 36 | 4r | BRYBYR |
| 32 | 5r | BBRYYR |
| 34 | 6b | YBRYRB |
| 42 | 7b | BBYRYR |
| 41 | 8b | BBRYRY |
| 35 | 9y | RBYRYB |
| 38 | 10r | YYRBRB |
| 39 | 11r | RRBYBY |
| 40 | 12y | RRYBYB |
| 31 | 13b | BBYRRY |
| 30 | 14b | BBRRYY |
| 5 | 15r | GGRYYR |
| 3 | 16r | GGYRRY |
| 10 | 17y | YYGRGR |
| 9 | 18r | YYRGRG |
| 13 | 19r | RRGYGY |
| 14 | 20y | RRYGYG |
| 1 | 21y | GGRRYY |
| 4 | 22y | RRGYYG |
| 2 | 23y | GGYYRR |
| 47 | 24r | GGBRRB |
| 43 | 25r | BBGGRR |
| 45 | 26r | BBGRRG |
| 53 | 27r | RRBGBG |
| 44 | 28r | BBRRGG |
| 54 | 29r | RRGBGB |
| 46 | 30r | BBRGGR |
| 11 | 31y | GGRYRY |
| 7 | 32g | GRYGYR |
| 12 | 33g | GGYRYR |
| 8 | 34g | RGYRYG |
| 6 | 35g | YGRYRG |
| 52 | 36g | GGRBRB |
| 56 | 37g | BBGRGR |
| 55 | 38g | BBRGRG |
| 48 | 39b | GBRGRB |
| 50 | 40b | BGRBRG |
| 51 | 41b | GGBRBR |
| 49 | 42b | RBGRGB |
| 15 | 43b | BBYYGG |
| 20 | 44y | YBGYGB |
| 16 | 45g | BBGGYY |
| 25 | 46g | GGBYBY |
| 17 | 47g | BBYGGY |
| 19 | 48w | GGBYYB |
| 18 | 49w | BBGYYG |
| 22 | 50w | BGYBYG |
| 21 | 51w | GBYGYB |
| 26 | 52w | GGYBYB |
| 24 | 53w | YYGBGB |
| 23 | 54w | YYBGBG |
| 27 | 55w | BBGYGY |
| 28 | 56w | BBYGYG |
| Old | New | Colour |
|---|---|---|
| 1 | 21y | GGRRYY |
| 2 | 23y | GGYYRR |
| 3 | 16r | GGYRRY |
| 4 | 22y | RRGYYG |
| 5 | 15r | GGRYYR |
| 6 | 35g | YGRYRG |
| 7 | 32g | GRYGYR |
| 8 | 34g | RGYRYG |
| 9 | 18r | YYRGRG |
| 10 | 17y | YYGRGR |
| 11 | 31y | GGRYRY |
| 12 | 33g | GGYRYR |
| 13 | 19r | RRGYGY |
| 14 | 20y | RRYGYG |
| 15 | 43b | BBYYGG |
| 16 | 45g | BBGGYY |
| 17 | 47g | BBYGGY |
| 18 | 49w | BBGYYG |
| 19 | 48w | GGBYYB |
| 20 | 44y | YBGYGB |
| 21 | 51w | GBYGYB |
| 22 | 50w | BGYBYG |
| 23 | 54w | YYBGBG |
| 24 | 53w | YYGBGB |
| 25 | 46g | GGBYBY |
| 26 | 52w | GGYBYB |
| 27 | 55w | BBGYGY |
| 28 | 56w | BBYGYG |
| 29 | 3y | BBYYRR |
| 30 | 14b | BBRRYY |
| 31 | 13b | BBYRRY |
| 32 | 5r | BBRYYR |
| 33 | 2y | RRBYYB |
| 34 | 6b | YBRYRB |
| 35 | 9y | RBYRYB |
| 36 | 4r | BRYBYR |
| 37 | 1y | YYBRBR |
| 38 | 10r | YYRBRB |
| 39 | 11r | RRBYBY |
| 40 | 12y | RRYBYB |
| 41 | 8b | BBRYRY |
| 42 | 7b | BBYRYR |
| 43 | 25r | BBGGRR |
| 44 | 28r | BBRRGG |
| 45 | 26r | BBGRRG |
| 46 | 30r | BBRGGR |
| 47 | 24r | GGBRRB |
| 48 | 39b | GBRGRB |
| 49 | 42b | RBGRGB |
| 50 | 40b | BGRBRG |
| 51 | 41b | GGBRBR |
| 52 | 36g | GGRBRB |
| 53 | 27r | RRBGBG |
| 54 | 29r | RRGBGB |
| 55 | 38g | BBRGRG |
| 56 | 37g | BBGRGR |

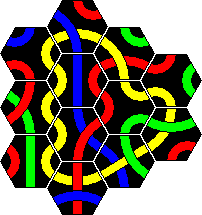
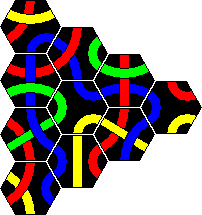
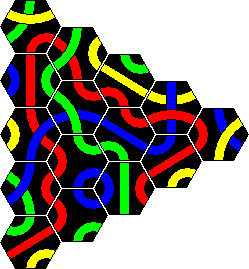
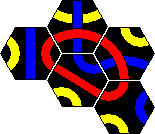
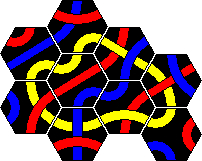
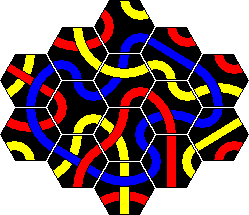
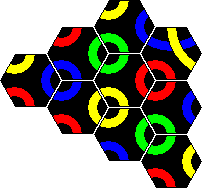
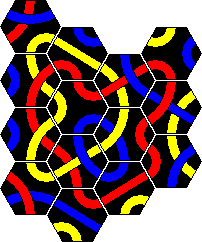
The first version of Tantrix was a puzzle consisting of 10 hexagonal tiles. The aim is to tile the pieces (without leaving holes) to make a single loop using all the parts of one colour and such that the edges of all adjacent tiles match colours. Any colour loop is possible. It is therefore three puzzles in one, one for each colour.
The tiles are shown below. I have shown them using the colours red, blue, and yellow. The colours of the real sets did vary however. I got one set with the aforementioned colours. For a present I received second set of 10 Tantrix pieces, but these used green instead of yellow. Other than that they are exactly the same.










The solutions of the red/blue/yellow loops are shown further down the page. You can click the link below-right to jump there directly.
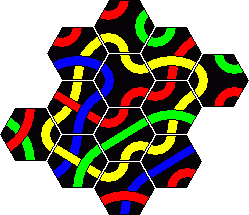
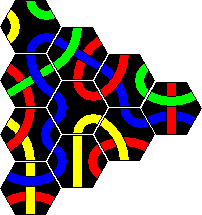
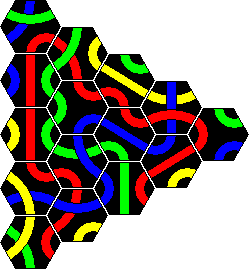
It is possible to combine two differently coloured Crazy Tantrix sets to make a larger puzzle. I have combined my red/blue/yellow and red/blue/green sets to make a large red loop. A blue loop is also possible, though more difficult. A solution to the red loop is given in the solutions section.
Solutions to the original puzzle
Tips on solving loop puzzles
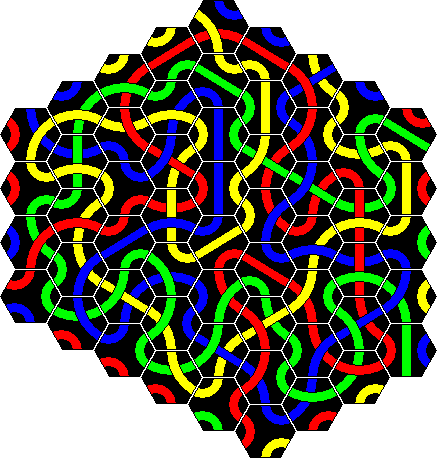
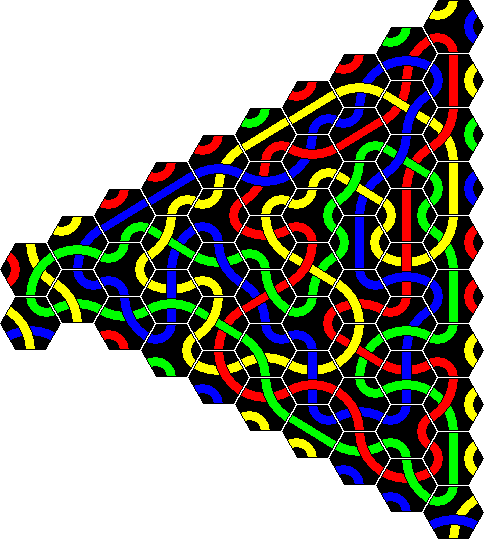
The background image used on this page consists of a repeated pattern using the ten tiles of the Original Puzzle. It was quite difficult to find a ten-tile shape that can be tiled easily. I do not believe that there is such a shape that tiles the plane with only translations, and that only shapes that need rotations as well are possible. What makes it harder is that the background image must be rectangular. In the end I plumped for the triangle shape shown below that combined with an upside down copy of itself forms a 4 by 5 diamond. By making sure its edges were such that the diamond could be tiled in a regular rectangular manner, the eventual background image would remain fairly small. Click the image to see the rectangular repeated pattern. I found several solutions, but this one is the only one I found that has infinitely long lines of all three colours, though it does have a loop. I did not find any with only loops or only lines that use ten tiles, but have not done an exhaustive search.
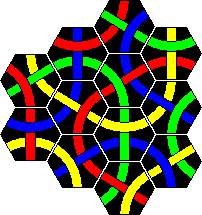
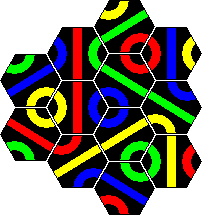
I did find a very nice 9-tile shape (3x3 diamond) that tiles the plane (without rotations) and has only loops, and another that has only lines. The trouble with these however is that they do not tile in a rectangular way, so the background image would have to be quite large and contain many copies if this shape (18 in fact), or be skewed in some way. The tiling patterns are shown below. Click on them to see the large rectangular tile that would be needed for a background.
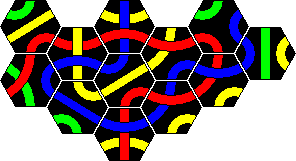
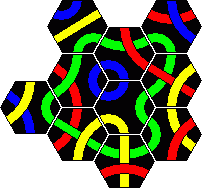
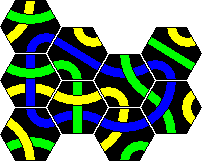
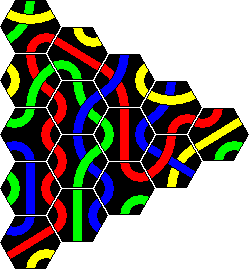
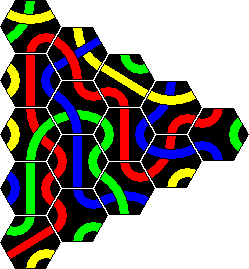
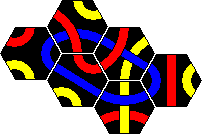
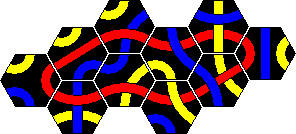
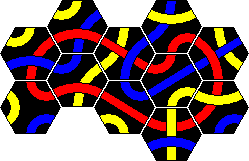
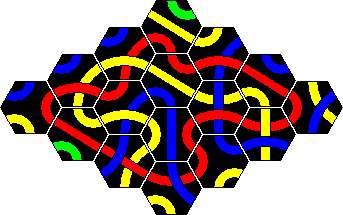
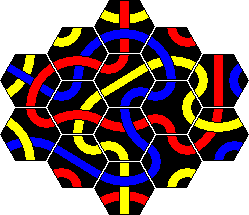
Tantrix Xtreme is a puzzle version of Tantrix similar to the original, but more challenging. It also consists of 10 hexagonal Tantrix tiles, but now four colours are used in the set, and the tiles are numbered on the back. The tiles are shown here:










Note that the exact colours may vary. In my set it is more purple than red, and uses white instead of yellow. For consistency I have used the four standard colours on this page however.
There are all together 10 challenges, from easy to rather hard. Start with
the tiles numbered 1-3, and make a single loop of one colour. The same rules
apply as with almost all other Tantrix puzzles - all adjacent tile edges
should match colour, and there should not be holes in the tile arrangement.
Once you have done a loop with tiles 1-3, then try to make a loop with 1-4,
and then 1-5 and so on until you eventually use all ten tiles to build a loop.
In most cases only one of the colours can be used for making the loop, the
others being impossible. In some cases, in particular the 10 tile loop, more
than one colour loop is possible.
 After those eight loop challenges, there are two difficult line puzzles. The aim
is to put the ten tiles in a triangle shape, but with the red or the blue colour
forming one long line through all the tiles. Both red and blue have solutions.
After those eight loop challenges, there are two difficult line puzzles. The aim
is to put the ten tiles in a triangle shape, but with the red or the blue colour
forming one long line through all the tiles. Both red and blue have solutions.
Solutions to the Xtreme Tantrix
Tips on solving loop puzzles
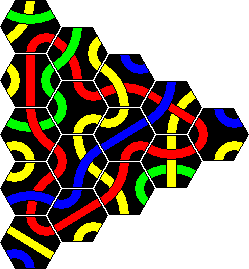
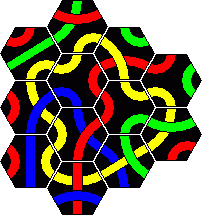
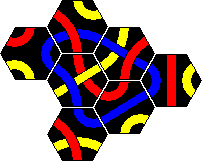
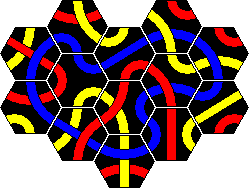
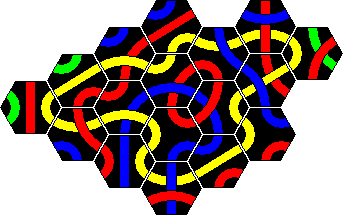
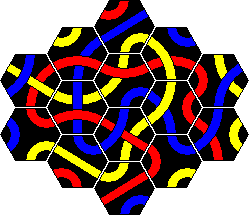
In the booklet that comes with the 56 tile set several puzzles are given. The tiles can be separated into 5 separate sets, which are called the 'Super 5' puzzles. They are called Junior, Student, Professor, Master, and Genius. Apparently these were sold separately as well.
In the Junior, Student and Master puzzles the aim is to make a loop of one colour, just like the Original puzzle. Of course, the loop must include all the tiles with that colour, and the tiles may not enclose a hole. In the Professor puzzle the aim is to make two simultaneous loops. Again each loop must use all the tiles of that colour. Tiles which have both chosen colours must therefore be incorporated in both loops. The Genius puzzle is extremely difficult, as now you must make two lines instead of loops. The restrictions that loops impose do not apply to this puzzle. It has two types of solutions (red/blue, red/yellow), and it took me about a week to find a solution for each. I thought there was essentially only one solution of each type, but Alexander Fronk sent me a second solution for the red/yellow lines.
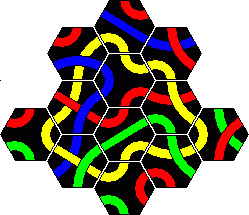
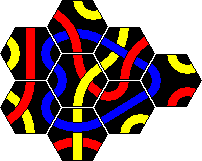
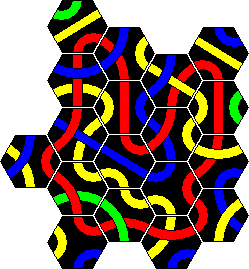
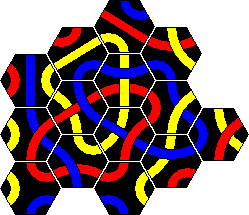
The booklet of the Tantrix game used to contain three pyramid puzzles. With these you have to use 15 tiles and they all have solutions in a pyramid shape, i.e. a size 5 triangle. In puzzle 1 you have to make a red loop, in puzzle 2 two loops using any two colours (like the Super 5 Professor puzzle), and in puzzle 3 two lines of any two colours (like the Super 5 Genius puzzle). Puzzle 3 is extremely hard to solve. The current booklet no longer contains these puzzles. The tiles to use are listed below:
Nowadays another set of puzzles is given. Like the Super 5 puzzles there are five puzzles that together make the full set of 56 tiles. The numbers engraved on the back of the tiles are painted in 5 colours, so that they can easily be separated into the 5 sets of tiles used. The puzzles are as follows:
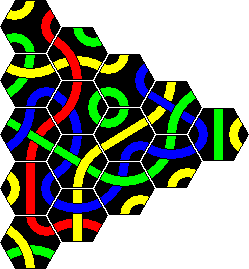
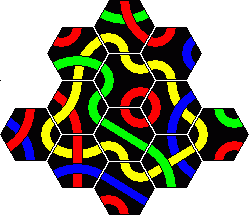
The Tantrix Discovery is very much like Tantrix Xtreme. It is a set of 10 tiles with which you can do several loop puzzles. They are exactly the tiles numbered 1 to 10 in the complete set (as it is sold now, i.e. the new numbering scheme). Start with the tiles numbered 1-3, which are yellow numbers, and make a single yellow loop. Then add tile number 4, which is a red number, and try to make a red loop. Continue on in the same way, each time adding the next tile and trying to make a loop of the colour which that number has.
If you have more than one Discovery set then you can combine them to make larger loops, again adding individual tiles in numerical order and making a loop of the colour given by colour of the tile number just added. This can continue to indefinitely large loops, but I will not give solutions to that.
The current booklet with the full set also says that you can continue by adding tiles from 11 onwards, all the way up to 30. In the solutions section you can find a solution for each of these loops. For completeness, here are the tiles used in the Discovery puzzles from the full set:
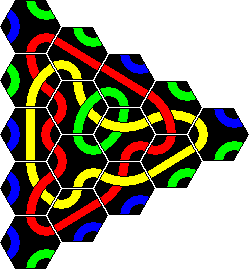
There are two so-called "unsolved" puzzles, using all 56 tiles.
1. The first is to find an arrangement with the four longest lines, one of each colour. Only the longest line of each colour counts, and the best is the one with the longest total length. The current record according to the Tantrix homepage is 146=40+37+35+34. Note that since all possible tiles are in the set, any solution can be rearranged such that the colours are swapped around.
It can be proved that 146 is the maximum attainable, so this puzzle has actually been solved.
Nobody has ever done so by hand without computer assistance.
Sketch of proof: Consider an arrangement with 4 lines of total length 146. A line of length n
uses n tiles, and therefore involves 2n tile sides. Of these, 2n-2 sides are internal, and 2 sides are
the endpoints. The 4 lines will therefore use 2·146-8=284 internal sides of tiles. The 56 tiles have
6·56=336 sides all together, leaving 336-284=52 sides along the outside of the arrangement. Longer
lines would leave fewer external sides. The size 5 regular hexagon with one edge shaved (i.e. a hexagon
with sides 5, 5, 5, 4, 6 and 4) is the shape with the smallest possible perimeter, namely 52. Therefore
the lines cannot be longer than 146.
The difficult step is proving that the hexagon shape has the smallest perimeter. I have proved this, in a
long and tedious manner as follows: first show that the best shape is nearly convex, i.e. has at most one
tile with one external edge. Then write the number of tiles in each row in a list, and show that with the
best shape the list will look something like this: 7, 8, 9, 10, 9, 8, 5, i.e. first strictly increasing
then decreasing and with successive differences equal to 1 except possibly for the last one. This leaves
only a relatively small number of possibilities, and of these the sequence 6, 7, 8, 9, 10, 9, 8, 7, 6, 5
is the best.
2. The second unsolved puzzle is to find the arrangement with the four longest loops. The current record is 136=38+35+33+30. In 2003 Jack Kuipers became the first person to solve this puzzle by hand without using a computer.
It can probably be proved that 136 is the maximum attainable.
Sketch of proof:Any shape
with 56 tiles must have some tiles with an odd number of external sides, because they cannot be arranged
in a triangle (tiles with 4 external edges are at a 60 degree corner, with 2 external edges along a
straight side of the arrangement). Each tile with an odd number of external sides must have
at least one line connecting to an internal with an external side. Thus any such odd corner will be the
start of a line leading into the arrangement, wasting internal sides which are better used for forming
loops. The best shape is therefore one with a small perimeter, but which has few odd corners and has its
odd corners close together.
Consider a size 10 triangle with one extra tile added anywhere on its side. This has perimeter 62, and
its two odd corners are adjacent so these waste only 2 internal sides. This leaves 336-64=272 internal
sides for a total loop length of 272/2=136. Any other shape with more odd corners that is more convex
will have a smaller perimeter but all internal sides gained are probably all wasted on the lines between
the odd corners. It is likely that no other shapes have more available internal sides.
Again the difficulty is proving that this shape is the best. I have not properly proved this.
 From the full set, take the 12 pieces which have a straight line and two bends. Try to make the shape
shown on the right - a triangle with sides of length 5 but with its tips missing. In other words, the
shape with rows of lengths 2,3,4,3.
From the full set, take the 12 pieces which have a straight line and two bends. Try to make the shape
shown on the right - a triangle with sides of length 5 but with its tips missing. In other words, the
shape with rows of lengths 2,3,4,3.
The Rock is a three-dimensional version of Tantrix. It has the shape of a truncated octahedron, which
has 8 hexagonal faces and 6 square faces. There are hexagonal and square Tantrix tiles which attach to these
faces, and the aim is of course to place all these tiles so that all the coloured lines match up. This means
that each colour will be one or more loops on the surface of the rock. Instead of taking the tiles off
completely and trying to solve it, it is also possible just to rotate the tiles in place which makes for an
easier puzzle.
The tiles are as follows:
Hexagonal tiles:
BBYRYR, BBRYRY, YYBRBR; BRYBYR, RBYRYB; RBBRYY, BRRBYY; BBRRYY
Square tiles:
BRBR, BYBY. RYRY, BBRR, BBYY, RRYY
This puzzle has only 5 solutions.
Before you read on, please be aware that these tips will make some of the puzzles quite easy and may spoil your enjoyment of the puzzle.
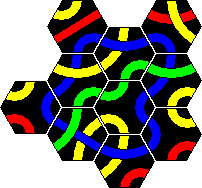
Here are three solutions of the original Tantrix puzzle, one of each colour. There are dozens of possibilities for each, so these are only examples.

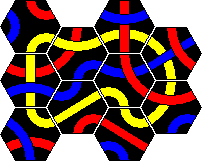
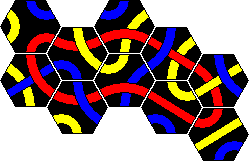
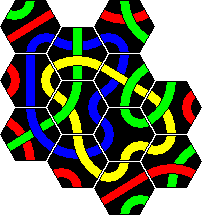
Here is a solution for a large red loop with two sets combined. A blue loop is a little more difficult, and I leave that to you.
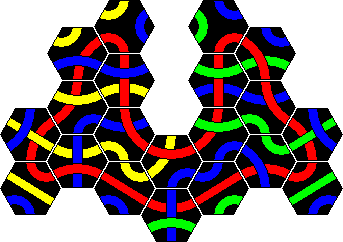
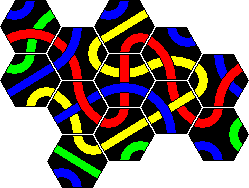
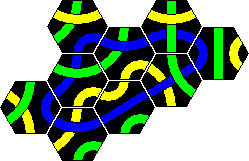
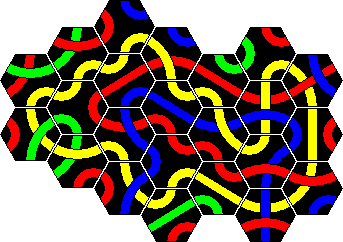
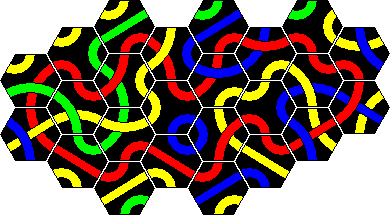
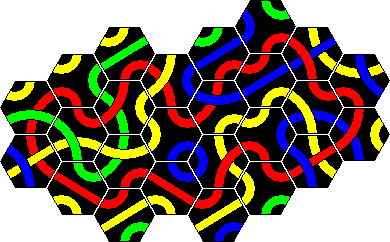
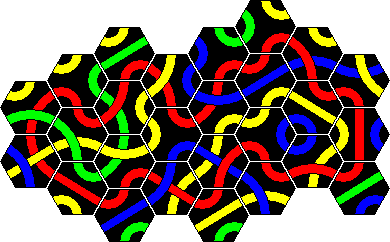
Here are solutions to the 8 loop puzzles. Two solutions are given for the 7 and the 10 tile loop, because two colours are possible. In all the other cases, only one of the colours can be used to make a loop.
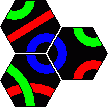
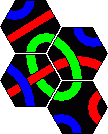

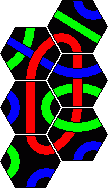
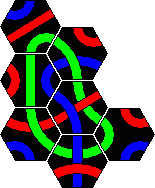
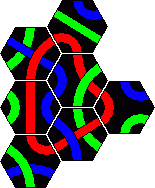
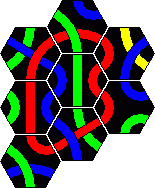
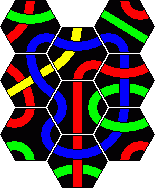
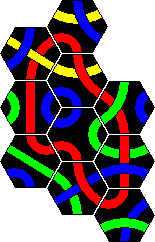
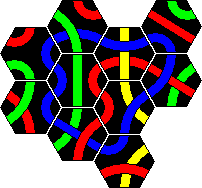
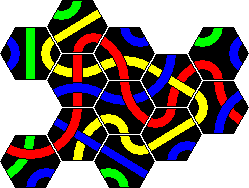
Here are the solutions to the 2 pyramid puzzles. There are essentially three solutions for a red line and only one for a blue line. These are shown below.
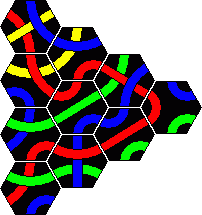
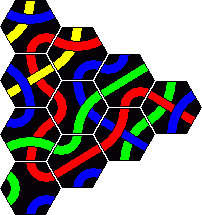
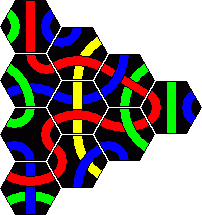
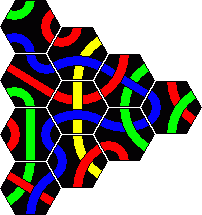
Minor variations are possible by rearranging one or more sets of tiles. For example in the first solution you could swap tiles 2 and 4, or swap tiles 5 and 7, or turn tile 1 around a bit, which leads to 8 variations. In solution 2 only tiles 3 and 8 on the corners can be trivially swapped. In solution 3 we can swap 3 and 5 as well as the trivial corners 2 and 6. There are six variations of the blue solution by rearranging the tiles from left and right columns (tiles 1-5).
While the professor and Genius solutions are essentially unique, the others have other solutions than those given here.