













This page is about seven related puzzles. They consist of a number of layers made of paper or plastic, divided into a number of cells. Each cell is coloured or transparent (or cut out). The aim is to stack the layers on top of each other to get a particular colour arrangement on front and back.
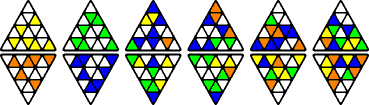
Transposer 6 has six triangular layers, and the aim is to make
each side a single colour. This can be yellow or orange on one side,
and blue or green on the opposite side.
The packaging claims it has 16,796,160 possible
combinations, though I make it one third of that, 6!·66/6
= 5,598,720. The division by 6 is in order to remove the orientations of
the combined packet.
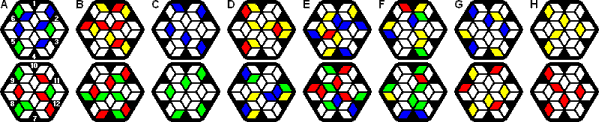
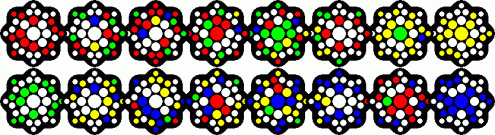
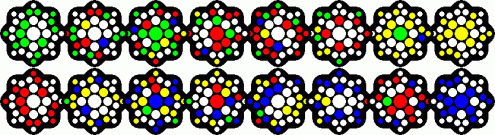
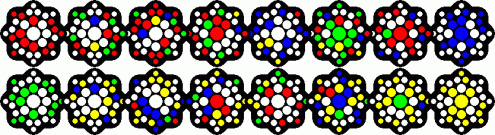
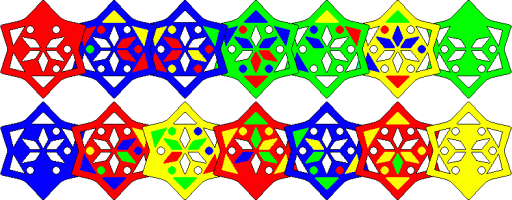
Transposer Tiffany has eight hexagonal layers, and the aim is to make each side a single colour. This can be green opposite yellow, or red opposite blue.
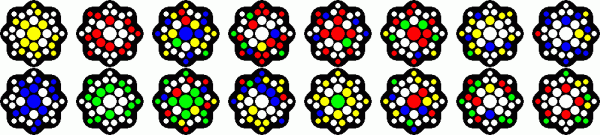
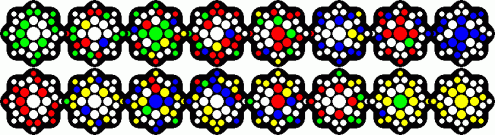
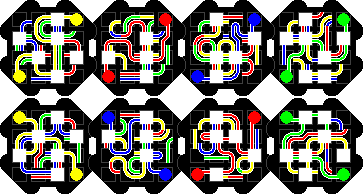
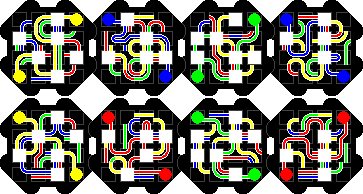
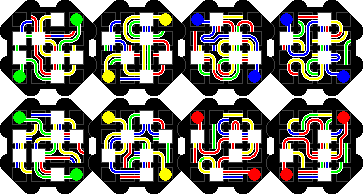
Transposer Bonbons has eight octagonal layers, and the aim is to make
each side a single colour. This can be green opposite yellow, green opposite
blue, red opposite yellow, or red opposite blue.
The packaging claims it has 48,318,382,080 possible combinations, though I
make it 8!·168/16 = 10,823,317,585,920. The division by 16
is in order to remove the orientations of the combined packet. Even if you
only count those combinations that have the two monochrome layers on the
outside, then you still have 2·6!·168/16 =
386,547,056,640 positions, eight times the listed number.
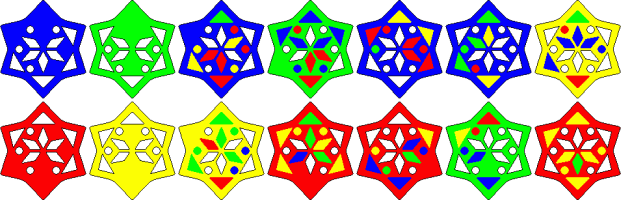
Transposer Genesis has seven heptagonal layers, and the aim is to make each side a single colour. This can be green opposite red, green opposite blue, yellow opposite red, or yellow opposite blue.
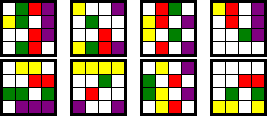
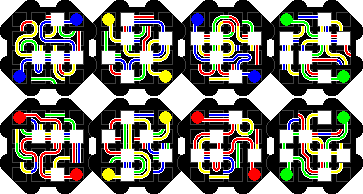
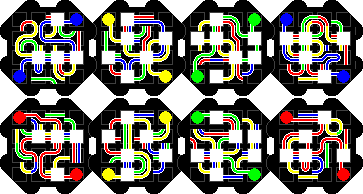
Kaboozle has four square layers, covered with various coloured paths. A solved position has on each side a path of a single colour. There are four colours, and every pair of colours can be chosen for the front and back paths, so there are six puzzles to be solved.
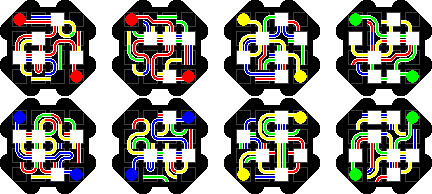
The Transposer puzzles are made by Albatross Games in the UK. They are patented by Chaim Raphael Weinreb on 19 July 2000, WO 99/15248 (and GB2345645, EP1021227, US5281986).
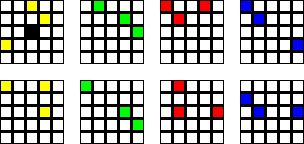
Trixxy has only four square layers, each consisting of 4 by 4 square cells. In the solved state, the front has one row of each colour, and the back has one column each colour. Trixxy is the trickiest of the puzzles on this page despite its low number of possibilities because every piece has rows/columns of each colour and this can be very misleading. It was invented by Dror Green and made in Israel.
Stained is a Japanese puzzle of this kind. It has only eight transparent square layers, each consisting of 5 by 5 square cells. Every layer has exactly three squares of one colour and the rest is transparent. Whereas in the other puzzles coloured cells can cover each other, here there are just enough coloured squares to go around, so the colours are never covered up. The aim is to do just that, make all 24 non-central cells to show a colour. Note also that unlike the other puzzles, here the front and back of each layer has the same colours, as even the coloured cells are transparent. The order of the layers does not matter. It has three solutions.
The following table compares the various attributes of these four puzzles.
| Puzzle | Shape | Layers | Colours | Cells | Avg. Filled | Number of arrangements | |
|---|---|---|---|---|---|---|---|
| Transposer 6 | Triangle | 6 | 4 | 16 | 8.67 | 6!·65 | =5,598,720 |
| Transposer Tiffany | Hexagon | 8 | 4 | 24 | 8 | 8!·127 | =1,444,738,498,560 |
| Transposer Bonbons | Octagon | 8 | 4 | 33 | 14.75 | 8!·167 | =10,823,317,585,920 |
| Transposer Genesis | Heptagon | 7 | 4 | 18 | 7.86 | 7!·146 | =37,948,861,440 |
| Kaboozle | Square | 4 | 4 | 16 | 5.5 | 4!·83 | =12,288 |
| Trixxy | Square | 4 | 4 | 16 | 8.5 | 4!·83 | =12,288 |
| Stained | Square | 8 | 4 | 24 | 3 | 87 | =2,097,152 |
Yellow-Blue solution:
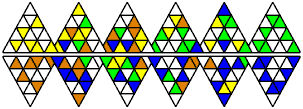
Orange-Green solution:
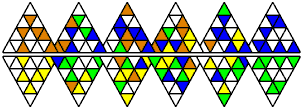
Yellow-Green solution:
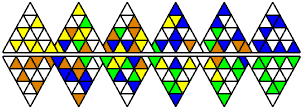
Orange-Blue solution:
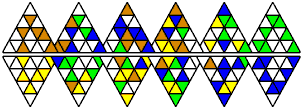
Blue-Red solution:
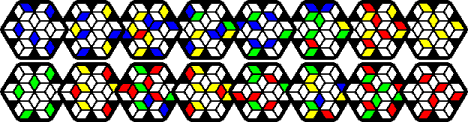
Green-Yellow solution:
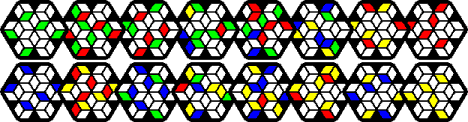
Red-Blue solution:
Green-Blue solution:
Red-Yellow solution:
Green-Yellow solution:
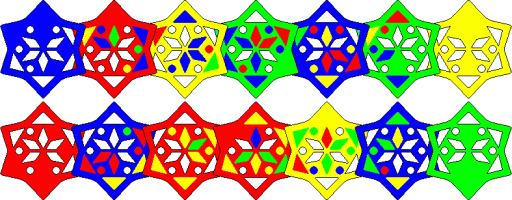
Blue-Green solution:
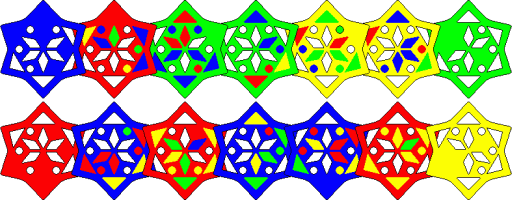
Blue-Yellow solution:
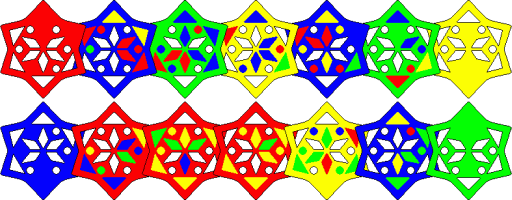
Red-Green solution:
Red-Yellow solution:
Blue-Green solution:
Blue-Red solution:
Blue-Yellow solution:
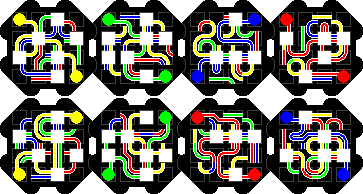
Yellow-Green solution:
Yellow-Red solution:
Green-Red solution:
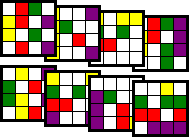

The first two solutions are similar, they just have red and yellow swapped. The third
solution has two adjacent red cells, but the first two solutions have no adjacent cells
of the same colour.