Jaap's Puzzle Page

Ultimate Skewb / Puzzleball

Ultimate Skewb

The puzzle is a variant on the Skewb which has a dodecahedral shape. A cube can be embedded in a regular dodecahedron so that its corners coincide with eight of the corners of the dodecahedron. This puzzle can be considered to be a regular Skewb cube which has been extended into a dodecahedron in the same way. It has 8 triangular corner pieces, and 6 square roof-like face pieces. The puzzle usually has only 6 colours, and opposite (parallel) faces have the same colour. When Meffert first made some of these, it was called the Pyraminx Ball.

This puzzle differs from the most other Skewb variants because here the orientation of all the pieces is visible. It is therefore the most difficult Skewb variant. On the regular Skewb face orientation is not visible, whereas on the diamond the orientation of the triangular pieces is not visible. Some puzzleball puzzles also have visible orientations on most pieces, and they may be solved in the same manner as the ultimate Skewb.

The number of positions:

There are 4 fixed corners with 3 orientations, 4 free corners with 3 orientations and 6 face pieces with 2 orientations, giving a maximum of 6!·4!·38·25 positions. This limit is not reached because:

This leaves 6!·4!·36·23 = 100,776,960 positions.

Every position can be solved in at most 14 moves. Thanh Vinh Nguyen was the first to calculate God's Algorithm, i.e. the shortest solution for each position. Many thanks to Thanh and Claude Crépeau for sharing these results. In the table below I have placed the results for all the Skewb variants together for comparison.

Moves Beachball Diamond Pyraminx Skewb M-H Pyramid Ultimate Skewb
0 1 1 1 1 1 1
1 8 8 8 8 8 8
2 48 48 48 48 48 48
3 252 288 288 288 288 288
4 930 1,632 1,728 1,728 1,728 1,728
5 884 8,568 9,896 10,248 10,128 10,248
6 37 36,114 51,808 59,304 57,780 59,976
7 74,799 220,111 315,198 305,483 346,740
8 16,547 480,467 1,225,483 1,239,266 1,958,850
9 220 166,276 1,455,856 1,879,631 10,297,604
10 15 2,457 81,028 237,320 39,466,215
11 32 90 778 46,217,578
12 21 2,417,060
13 615
14 1
Total 2,160 138,240 933,120 3,149,280 3,732,480 100,776,960
Avg Depth 4.2694 6.6921 7.7955 8.3636 8.5081 10.352

The single antipode on the ultimate Skewb is the superflip, the position with all six faces flipped but otherwise correct.
In Sloane's On-Line Encyclopedia of Integer Sequences these are included as sequences A079763, A079765, A079744, A079745, A079746, and A079874.

Links to other useful pages:

Meffert's puzzles Uwe Meffert's pages. He produces the Pyraminx, the Skewb and many variants of it.
Meffert's page. Contains the solution provided in the booklet for the standard Skewb.
Meffert's page. Contains the solution provided in the Creative Puzzleball booklet.
Meffert's page. Contains the solution provided in the Ultimate Skewb booklet.
David Joyner's page. A catalogue of move sequences.

Notation:

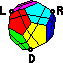
Note that the corners fall in two classes; four left-handed and four right-handed ones. You will only turn one of these classes, so that these will be considered fixed in space while the other 4 free corners move about. Hold the puzzle so that the tetrad of fixed corners point left, right, down and back. Denote clockwise moves at the corners by L, R, D and B. Anti-clockwise turns are denoted L', R', D' and B'. Any face can be specified by two letters, e.g. DR is the face between the down and right fixed corners. The other 4 corners can similarly be specified by 3 letters.

There now follow 2 different solutions. The first solution below closely follows that of the pyraminx.

Solution 1:

3 top corners3
3 top faces14
bottom corner1
3 bottom faces8
4 free corners13
total:39 moves

Phase 1: Solve 3 top corners

Rotate L, R, and B so that their orientation is correct. On the Ultimate Skewb these corners do not have any sides in common, but as opposite faces of the solved puzzle usually have the same colour, then the three corners can be turned so that their matching colours are on opposite faces.

Phase 2: Solve 3 top faces

  1. Find a face piece at the D corner which does not belong there.
  2. Hold the puzzle so that the belongs at the LR position.
  3. Rotate D to bring the piece to the back so that it is in the RD or BD position.
  4. Use one of the following sequences to place the piece correctly:
    1. Move BD->LR:   Do LDL'.
    2. Move DB->LR:   Do R'DR.
  5. Repeat the above until all three top faces are correct. If necessary, you can use one of the above sequences to displace incorrectly placed faces from the top layer.

Phase 3: Solve the D corner.

Simply rotate D to orient its corner correctly. See the remarks in Phase 1. If you are solving a puzzle ball and the D triangle has no visible orientation, then rotate D so that either all 4 free moving corners are correctly positioned, or such that none of them are (If there are identical free corners then keep in mind that they may be considered to be swapped).

Phase 4: Solve the D faces.

There are now only a few possibilities for the last 3 faces left:
1. To cycle RD->LD->BD->RD:   Do: R'DRDR'DR.
2. To cycle RD->BD->LD->RD:   Do: R'D'RD'R'D'R.
3. To flip RD->DR, LD->DL:   DRD'LD'L'DR'.
4. To cycle RD->DL->DB->RD:   RLDL'D'R'
5. To cycle RD->DB->DL->RD:   RDLD'L'R'

Phase 5: Solve the final 4 corners.

  1. If the corners are positioned correctly, but only need to be oriented properly, then the following sequences can be used. You will probably need to rotate the whole puzzle to get into one of these positions:
    1. LRD->DLR, RBD->DRB, BLD->DBL:   B' RD'R'D BD' L'R'L'RL' D
    2. LRD->RDL, RBD->BDR, BLD->LDB:   D' LR'LRL DB' D'RDR' B
    3. BLD->DBL, RBD->BDR:   LDL'D' R B'D'BD R'
    4. LRD->DLR, RBD->BDR, BLD->LDB, LRB->RBL:   D' LR'LRL DB' D'RDR' B
  2. If the corners are not in the correct position, then one of the following sequences will do:
    e. DLR->BRL->DLR, LDB->RBD->LDB:   DR'D' L'D'LD R D'L'DL
    f. DLR->LBR->RDL, LDB->DRB->DBL:   DL' D'RDR' L RD'R'
    g. DLR->RLB->LRD, LDB->BDR->BLD:   B'LD'L'D B D'LDL'
    h. DLR->BRL->DLR, LDB->DRB->LDB:   DR'L'B'LRDLBL'D
    i. DLR->LBR->RDL, LDB->RBD->DBL:   R D R'LRL' D' LR'L'
    j. DLR->LBR->RDL, LDB->BDR->DBL:   L'R'L B' L'RLR' B R
    k. DLR->LBR->LRD, LDB->BDR->BLD:   L RD'R'D L' D'RDR'
    l. DLR->LBR->RDL, LDB->DRB->LDB:   L'R'DRL BRD'R'B'
    m. DLR->LBR->RDL, LDB->BDR->LDB:   LDBL R' L'B'D'L' R

Solution 2:

Phase 1:

Do any standard Skewb solution. This solves everything except the face orientations.

Phase 2: Orient the faces.

Do one of the following sequences to flip the faces correctly:
1. Flip DL, DR:   B'LB D'R'DR BL'B' RDR'D'
2. Flip DB, LR:   DBL B'R'BR D'L'B' LRL'R'
3. Flip DL, DR, DB, LR:   B' D'RD' L'B'R DB'D LR
4. Flip DL, DR, BL, BR:   DRD B' RD'LD'R'D B' DR'DB'L'
5. Flip DL, DR, DB, LR, BL, BR:   DRD' L'B DRD' L DB'DL'RDL