



The Varikon Box 2×2×2 puzzle is a 2×2×2 sliding cube puzzle,
similar to the 3×3×3 versions Peter's Black Hole,
IQube, and Magic Jack. It is a transparent box containing 7 cubes and a space.
The cubes can easily be moved by tilting the box.
The puzzle pictured above has white cubes, and each side has a red or blue spot. When
solved, all the blue spots are on the outside, with only the space showing three red
spots. There is also a version made of red plastic with white and blue spots.
There is a tiny hole near one corner of the box, into which you can insert a small
rubber pin. This prevents the puzzle from getting mixed up accidentally.
One of the earliest versions of this puzzle is the BloxBox, invented by Piet Hein around 1972.
The Minus Cube is a Russian version of this puzzle with a different colour scheme. Its
7 cubes are identical, all having three white faces (of which two are opposite
each other) and three faces of another colour. Their orientations are not all the same, and
the aim is to arrange it so that whichever side of the puzzle you look at you will see 4
squares that match in colour.
There are at least two versions of this puzzle. The red and white one was made in Moscow, and
the blue and white version in Sverdlovsk (now Yekaterinburg). The latter is more difficult
as it has fewer solutions. There also seems to be a black and white one, but I don't know
what pattern it uses.


The Varikon Box was invented by Csaba Postasy, Gabor Eszes, and Miklos Zagoni. The German version of its patent, DE 3,027,556, was published on 19 June 1981.
If your browser supports it, you can click on the link below to play with a Javascript version of the Varikon Box 2×2×2.
There are 7 loose cubes and a space. Any even cube permutation is possible, but no odd permutations, so for any position of the space there are 7!/2 cube positions. This gives 8·7!/2 = 20,160 positions for the Varikon Box. It has only one solution.
The red Moskow Minus Cube has 3 identically oriented pieces, so it has 8·7!/3! = 6,720 positions. It has 16 solutions. The blue Sverdlovsk Minus Cube has two pairs of identically oriented pieces, so it has 8·7!/(2·2) = 10,080 positions. It has only 2 solutions.
Below is a table that shows how many positions there are at each distance from the starting position of the Varikon Box. It shows that no position needs more than 19 moves to solve (12.971 on average).
|
|
There are a three observations that will greatly simplify the solving process.
1. It seems like this puzzle has two solutions - blue on the outside, or
red on the outside. This is not so, as only one of these can be solved. Trying
to put the wrong colour outside will leave you with a position where two cubes
need to be swapped, and that is impossible. The version shown above should have
blue on the outside.
2. The small cubes have different colours on opposite sides. This allows you
to easily determine what the colours are on a cube's hidden sides, and therefore
to determine where in the solved position that cube belongs.
3. The small hole in the outer box shows which corner will be empty in the
solved position.
The Moskow Minus Cube has 16 solutions, two for each location of the blank space. To make this puzzle more difficult, you can choose which corner to put the space before starting the solve.
Here are four solutions that are only a few moves away from each other.

If you have chosen where to put the blank space, exactly one of these four solutions is
possible. You can determine which one by looking at the orientation of the three identical pieces,
which is different in each solution.
The same solutions can also be done in mirror image:

The other eight solutions are essentially the same but with the box turned upside down. Unless the box is marked in some way, it is not possible to distinguish these from the above solutions, but it does make it easier to solve.
The Sverdlovsk Minus Cube has 2 solutions which are mirror images of each other. You can get from one solution to the other by sliding just three cubes.
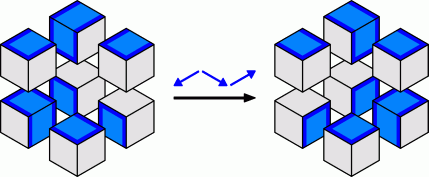
If you were to open the box and to reorient the cubes inside, there are only 38 ways to do this that have a solution (up to rotation, mirror images are considered distinct). Some of these are mirror images of each other, or are the same if their colours are swapped.