Yours for Improvement,
"Numeri Mundum Regent"
![]() THE
THE ![]()
ARITHMACHINIST
A
PRACTICAL SELF-INSTRUCTOR
IN
Mechanical Arithmetic
BY
HENRY GOLDMAN,
AUTHOR AND INVENTOR
OF
Advanced System for Locating Errors,
Self-Checking Trial Balance and Blank Books,
Short Methods for Computing Interest and Discount,
New Method for Averaging Accounts,
Security System for Preventing Forgeries,
Instantaneous Index, Automatic Binder,
Etc., Etc.
CHICAGO:
The Office Men's Record Co.,
.. 1898 ..
The engravings in this work being photographic reductions of
larger cuts, may be advantageously viewed through
a magnifying glass, if an examination of
minor details is desired.
COPYRIGHT, 1897, BY HENRY GOLDMAN.
All Rights Reserved.
Address all communications intended for the Author to
HENRY GOLDMAN,
Author and Inventor,
143-149 La Salle Street, Chicago.
PREFATORY.
THOUGH at different times printed directions for the manipulation of special calculating devices have been published, these presented the subject in such a limited and one-sided manner as to make a more thorough and comprehensive treatise of Mechanical Arithmetic not only desirable, but necessary. "The Arithmachinist" is the significant title chosen for this book, which is intended to serve as a practical self-instructor in a comparatively new branch of an old science, and particularly to popularize the adoption of machine methods in practical accounting. This has become possible with the advent of the Arithmachine, the first and only rapid and reliable Computing Machine of small dimensions and large capacity, which is low in price and noiseless in operation, and therefore answers the popular demand and practical requirements in every essential particular.
The purpose of this book, however, is not merely to take the place of a thorough instructor in the practical manipulation of the Arithmachine, but to teach the science of Mechanical Arithmetic in an exhaustive and interesting manner. It presents an illustrated, historical and technical review of the subject of machine computation; explains the reasons why up to the present it did not enter as a factor in modern business economies; states the causes of failure of computing apologies and gives complete instructions in the use of the Arithmachine, as a means of performing all arithmetical operations with accuracy and speed, offering at the same time labor saving methods for ascertaining and verifying results, entirely original with the Author, and not contained in any other work published. The many valuable points of information to be gleaned from the pages of this book will therefore not only prove beneficial and instructive to Arithmachinists, that is, users of the Arithmachine, but give a knowledge and appreciation of the practicability and utility of mechanical appliances in a hitherto untried field, and the possibility of substituting matter for mind, or rather physical force, for mental energy. The importance and helpfulness of such substitution in an age, in which the struggle for existence and supremacy taxes the nervous system to the utmost, must be at once apparent to all who give the subject any consideration.
- 4 -Methods of computation which are perfectly natural to the mental calculator are almost inapplicable to the machine, and vice versa, and this points out the radical difference and principal difficulty in writing a really helpful work on Mechanical Arithmetic, taking the textbooks now in use, either as guide or starting point. For it should always be borne in mind that in Mental Arithmetic the calculator is controlling his own efforts. While in Mechanical Arithmetic the operator is simply directing the workings of the machine, which for the time being assumes a separate and distinct personality.
About 95 per cent of the accounting work required by mercantile, manufacturing and banking houses consists of addition, and for this no more serviceable mechanism has ever been devised. It adds all columns at the same time and particularly prevents errors caused by carrying wrong hundreds or crowding two figures into one column, a frequent source of trouble, experienced by mental calculators. It further permits giving immediate attention to other important matters while engaged in adding long columns, without loss of time or the least risk or danger of making mistakes, thereby proving the old saying, "There is nothing so deaf as an adder," false and out-of-date. It performs subtraction with greater ease than other computing machines, particularly on account of the introduction of the double complemental scales, which is also fully protected by our letters patent, and represents a scientific achievement of considerable merit in itself. In multiplication the Arithmachine saves the carrying and adding of the partial products, and in division it multiplies the divisor by the quotient figures and subtracts the products simultaneously. Similar advantages are gained in squaring and cubing numbers, extracting square and cube roots, etc.
The Arithmachine can also be advantageously employed in combined operations, such as, for instance, balancing accounts, in which the balance is obtained directly, without first ascertaining the totals of both sides; in computing interest, discount, etc. In averaging accounts and all computations, in which a number of products are added together and the sum divided by the total, of a number of items, the final result is found by a single continuous process, which is a great step forward from the cumbersome mental and manual processes now in vogue. With the aid of simple attachments, chain covers, digit shutters, bar stop and decimal point, calculations with fractions and denominate quantities can be performed with ease and without the strain and effort attending the methods generally practiced. It can be used with advantage in listing, aggregating, etc., separate or scattered items; and in conjunction with interest, discount, - 5 - exchange, etc., is well as logarithmic, trigonometric, etc., tables, for the various arithmetical operations, occasioned by their use.
It is free from the objections which may be raised against other computing devices. It is low in price, costing less than one-fifth of the price of other computing machines, which only do part of its work, and that less satisfactorily. It is light in weight, about equaling that of an ordinary paper weight, and so small in sire that it can be easily covered by the palm of the hand. It is practically noiseless in manipulation, the sound produced by it resembling that of winding a watch. It can be conveniently held in the hand, fastened to the desk, moved over a blank book column, suspended on a hook or carried in the vest pocket.
It acts as a guide to the figures to be operated on and overcomes the awkward and annoying necessity of continually changing the range of vision from paper to machine and vice versa. The same glance which takes in the figures controls the operation of the Arithmachine, which corresponds in width and general arrangement with a regular blank book ruling. It can be operated by one or two persons, or with one or two hands, as may be required or prove desirable.
It is strongly and durably constructed, being composed entirely of metal, every working part properly strengthened and every wearing part made of steel, capable of performing about ten times the work actually required of it, which enables us to absolutely and unreservedly guarantee the Arithmachine for two years, while with proper care and usage it may last a lifetime. It is handy and graceful in turn, highly finished, an ornament to any desk as well as a necessity in every office.
The cashier of a leading financial institution, after thoroughly examining the Arithmachine, expressed himself as follows: "Yours is the machine we have been waiting for. It answers the most important requirements of a practical computing machine, and is particularly desirable, as it can be taken to our books, instead of compelling us to take our books to the machine. We can use twenty-five of them in this bank.
The operation of the Arithmachine is more natural and convenient than writing, while calling into play other muscles of the hand and forearm, and relieving those employed in writing, thereby preventing and curing writers' cramp. It saves at least one-third of the mental and physical energy expended in writing, the placing of ciphers being entirely avoided, not to speak of the fact that every significant figure is registered by a single, short and straight movement - 6 - of the stylus-pencil. It does away with the nerve-racking noise, wear and strain, incidental to the incessant pounding of numberless keys with the fingertips. The movement is easy, smooth, straight, forward, horizontal, continuous and natural, furnishing at the same time a light and healthful exercise.
The eyes are rested, because in place of a large and bewildering array of constantly moving and rebounding keys, the operating surface of the Arithmachine always presents the appearance of complete repose, the movement of the mechanism being so even and instantaneous as not to be noticeable. The number of sections being limited to the number of columns in the machine, and the operation of each section being completed before another section can be brought into action, the factor of simplicity is combined with that of safety against errors, not possessed by other machines, having either a multiplicity of keys, or keys requiring separate and distinct depressions of varying depths, in order to register accurately.
The practical manipulation of the Arithmachine, especially as far as the four species of arithmetic are concerned, can be acquired in less than an hour's time, while after a few days practice or actual use considerable confidence and speed are easily attained. It brings the ability of rapid and correct computation within the reach of everybody, and makes the remarkable skill of the lightning calculator, that of adding a number of columns simultaneously or multiplying numbers without first setting down the partial products, an easy attainment for school boys less than ten years old. And it argues strongly in favor of Mechanical Arithmetic that our boys and girls, after eight years' drilling in mental and manual arithmetic, are far from being equipped for the practical requirements of the counting room, while any one can become expert in the operation of the Arithmachine with a few hours' practice. If the sole purpose of education consisted of "Mental Discipline," so-called, the slowest and most awkward methods of computation would certainly be preferable, and as a matter of fact the brand of arithmetic commonly dispensed in our schools represents "Mental Discipline" with a vengeance. If, on the other hand, practical efficiency is a desideratum in modern education, Mechanical Arithmetic undoubtedly deserves fair and unbiased consideration on the part of teachers and parents as well.
It is bound to open now channels of employment for those who on account of their arithmetical difficulties or limitations have been debarred from higher accounting or office work, while in time it is very likely to throw out of employment those who wish to stem the - 7 - tide of progress; by stubbornly refusing to accept the advantages and facilities derived from mechanical computation. Its field of usefulness is as broad as that of business and the public schools, and far from being only beneficial to concerns who deal with large amounts exclusively, it will prove a special blessing to those who have little figuring to do, but are not fully prepared to do that little.
In short, we believe that the Arithmachine is unquestionably the most desirable and practical computing machine known, capable of performing the arithmetical work required by accountants, actuaries, bookkeepers, business men, clerks, scientists, students, teachers, etc., with accuracy and speed and without mental strain or straining physical effort.
Naturally a new invention has to overcome some popular prejudices, and a computing machine is no exception to the rule. After disposing of those objections which may be properly urged against other computing devices in particular, it is well to discuss and dispel the principal objections raised against the adoption of computing machines in general.
Some argue that computing machines destroy the mental faculty of computation. To this we simply reply that the reverse is true. They permit of the highest mental activity and development, harmoniously blending the operation of the hand with that of the mind, and thereby producing better results with less effort and fatigue. Modern educators fully appreciate the advantages of manual training in other branches and certainly arithmetic must, with proper facilities, be susceptible of similar treatment. Mechanical Arithmetic being an important branch of mathematics, full of valuable, interesting and instructive features, necessarily broadens the mental horizon of every one who becomes familiar with it, and it is difficult to comprehend how those who have mastered this scientific knowledge should become intellectually interior to those who are ignorant of it. Nor need anyone fear that the purchase or adoption of a practical computing machine reflects discreditably upon one's mental ability of computation. The world has advanced to a point where the users of improved mechanical appliances, whether in the office, the shop or the farm, are considered superior in accomplishment and efficiency to those who struggle along with old and antiquated tools and methods. Others, less old-fogy, say that while the machine may be very desirable and satisfactory in its workings, it does not furnish a proof of the accuracy of the results arrived at. The answer to this is that the machine works with proverbial "mechanical accuracy." It cannot make a mistake! Any possible mistake must be that of the operator, and there are ten chances for the mind to go - 8 - wrong before one is offered to the hand. The Arithmachine reduces computation to the act of reading, and it is evident that the tired brain is much more likely to report a wrong result, than that the tired hand is apt to place a wrong figure. In addition to this the various processes by which results are proved mentally, can be applied with greater facility to the machine, and the best methods adapted for this purpose are also briefly described in this work. It therefore appears that this argument speaks rather in favor of the Arithmachine, and against the cumbersome mental and manual processes now employed.
Last, but not least a few contend that after all "The old way is the best," not knowing or not having experienced the advantages of the new way. This is the only objection which will not yield to reasons! It is the argument which has preserved the quill pen, the tallow, candle, the stage coach, etc., against the invasion and encroachment of the typewriter, the electric light, the railroad, and other "new-fangled ideas." It proves our civilization a grand mistake and the barbarous state the ideal condition of man! It is true, but fortunately with an ever decreasing number of people. With malice toward none and charity tor all, we are not particularly catering to this class.
"The Arithmachinist," while necessarily condensed to serve as a handbook, and small in form to conform with the Arithmachine (Instructions for the more bulky computing machines ought to be printed on sheets of newspaper size), is the result of careful thought, study, investigation and research and will, it is hoped, not only prove an interesting and instructive contribution to the Literature of Accounts, but at the same time pave the way to a more exhaustive work on the subject.
In conclusion, acknowledgments are due for many valuable and important sources of information, particularly the Century Dictionary, Davies' Mathematical Dictionary, Knight's Dictionary of Mechanics, as well as numerous books, magazines, patent reports, pamphlets, circulars, etc, to the authors, publishers and compilers of which we herewith tender our sincere thanks!
THE AUTHOR.
CONTENTS
| Introductory. | PAGE. | |
|---|---|---|
| Scope and Purpose | 11 | |
| Elementary Arithmetic and Higher Mathematics | 11 | |
| Practical Methods | 12 | |
| Mental or Manual Discipline | 12 | |
| The 3 Rs and the 3 Ms | 12 | |
| Branches of Arithmetic | 13 | |
| Explanatory. | ||
| Importance and Utility | 14 | |
| Information and Prejudice | 14 | |
| Arithmo-Mechanics and Mechanical Arithmetic | 14 | |
| Origin of Terms | 15 | |
| Good Names | 15 | |
| Historical. | ||
| Early History | 16 | |
| Mensa Pythagorea | 17 | |
| Greek and Roman Notation | 18 | |
| Euclid, Diophantos and Boethius | 18 | |
| Roman Abacus and Chinese Suan-Pan | 20 | |
| Hindu or Arabic Notation | 21 | |
| Saccarium and Exchequer | 22 | |
| Tally System | 22 | |
| Sacro-Bosco and Nemorarius | 24 | |
| Adam Reese and Petrus Apianus | 24 | |
| Invention of Decimal Fractions | 24 | |
| John Napier and "Napier's Bones" | 25 | |
| Blaise Pascal and Samuel Morland | 26 | |
| Leibnitz, Poloni and Leupold | 26 | |
| Newton, Euler and Lagrange | 26 | |
| Babbage, Scheutz and Donkin | 27 | |
| Thomas' Arithmometer | 29 | |
| Alexander and Davies | 29 | |
| Nineteenth Century Development | 29 | |
| Present Conditions | 30 | |
| Technical. | ||
| Classification of Computing Machines | 32 | |
| Fingers and Figures | 32 | |
| Primitive Appliances | 32 | |
| Disk Devices | 34 | |
| Tape Contrivances | 35 | |
| Bar Machines | 36 | |
| Crank Machines | 37 | |
| Key Machines | 39 | |
| Listing Instruments | 42 | |
| Slide Rules | 43 | |
| Goldman's Arithmachine | 44 | |
| Arithmetical. | ||
| Practical Requirements | 46 | |
| Original Features | 47 | |
| Advanced Methods | 48 | |
| Combined Processes | 49 | |
| New Principles | 49 | |
| Accountant's Insight and Mechanic's Skill | 50 | |
| Arithmetical Mixtures | 50 | |
| PAGE. | ||
| Catch Question | 51 | |
| Educational Possibilities | 52 | |
| Mechanical. | ||
|---|---|---|
| Practical Consideration | 53 | |
| Elements of Success | 53 | |
| Conception and Execution | 54 | |
| Difficult Problem | 54 | |
| Mechanical Construction | 55 | |
| Out-of-Pocket Machines | 57 | |
| Patent Claims | 57 | |
| Operating Mechanisms | 57 | |
| Hygienic Advantages | 58 | |
| Descriptive. | ||
| Proportions and Dimensions | 59 | |
| Chain-Board and Indicator Opening | 59 | |
| Double Numeral Scales | 60 | |
| Attachments and Accessories | 62 | |
| Curved Pencil Stylus | 64 | |
| Modern Sphinx | 65 | |
| Directive. | ||
| Necessity of Directions | 66 | |
| Treatment | 66 | |
| Total Abstinence | 67 | |
| Vest Pocket Carrying Case | 68 | |
| Supply and Demand | 68 | |
| Operation | 70 | |
| Manipulation of Stylus-Pencil | 72 | |
| Resetting to Zero | 73 | |
| Desirable Positions | 75 | |
| Utilization of Attachments | 76 | |
| The Arithmachine Grip | 78 | |
| Instructive. | ||
| General Observations | 79 | |
| Mechanical Notation | 80 | |
| Double Complemental Scales | 81 | |
| Machine Addition | 83 | |
| Machine Subtraction | 90 | |
| Machine Multiplication | 93 | |
| Machine Division | 98 | |
| Combined Operation | 101 | |
| Common Fractions | 103 | |
| Denominate Quantities | 105 | |
| Miscellaneous Computations | 108 | |
| Powers and Roots | 110 | |
| Logarithms | 114 | |
| Correction of Mistakes | 116 | |
| Machine Proofs | 118 | |
| Speed Drills | 120 | |
| Conclusive. | ||
| Mind and Matter | 125 | |
| Truth and Fiction | 125 | |
| Size and Price | 127 | |
| Progress and Poverty | 128 | |
| Prospect and Retrospect | 128 | |
| Announcements | 129 | |
| Guarantee, Order Blank and Rebate Coupon | 158 | |
INTRODUCTORY.
IT would transcend the scope and purpose of this work and not be in keeping with its greatest utility, if the compilation of a complete and exhaustive arithmetical text-book were attempted. It is our aim rather to present the fundamental principles and operations of Mechanical Arithmetic, to illustrate some of their most important applications and to eliminate any information which may be either presupposed or can be easily found in numerous publications. On the other hand we will not be content to state rules which are to be blindly followed, or give directions without explaining the "why" and "wherefore," whenever necessary, so that the science of Mechanical Arithmetic may be thoroughly understood, and not merely mechanically practiced.
Contrary to the opinion of some, who have presented this subject in a very crude and bungling manner, it will become self-evident that no knowledge of higher mathematics nor any deep mathematical insight is required to comprehend and master any and all processes of mechanical computation. It is Elementary Arithmetic, pure and simple, and to even talk of higher mathematics in connection with it, only serves to exhibit one's ignorance. In fact, less mental development is required to understand the fundamental processes of Mechanical Arithmetic than is necessary to become conversant with the equivalent processes of Mental and Manual Arithmetic, which are easily learned by boys and girls from six to ten years old, certainly before even an inkling of - 12 - higher mathematics is acquired. And this is as it should be. For if Mechanical Arithmetic means anything, it stands for less mental effort, not only in its practice; but also in its acquisition.
Another characteristic feature of this work is the teaching of the most important applications of principles and processes in a thoroughly practical manner - rules and methods which are in accord with modern development and the actual requirements of the counting room. To offer in a book treating of Mechanical Arithmetic, which ought to be the incarnation of modern thought, adaptations and variations of the antiquated and round-about methods still found in many of our school books, and perpetuated with the beautiful excuse of Mental Discipline," appears to us a serious mistake. With equal reason could we advocate the most awkward machine methods for the sake of "Manual Discipline." We prefer to recommend dumb-bells and outdoor exercise, as benefiting mind and body to a greater extent than either.
In this connection it may be well to add that our public school in teaching the three Rs, ought to divide the last of the Rs into the three Ms, which are Mental, Manual and Mechanical 'Rithmetic. Certainly in the higher grades, and particularly in those institutions where the preparation for the duties of business life is aimed at, instruction in Mechanical Arithmetic would form a very interesting and helpful feature. And in teaching this new science such methods should be selected, which take into consideration the natural limitations of the mind, the hand and the machine, as only by a harmonious blending of the three instrumentalities the best and most satisfactory results can be achieved. Mental Arithmetic one is insufficient, as it overtaxes the memory and therefore becomes unreliable; Manual - 13 - Arithmetic alone is undesirable, as it is cumbersome and cannot keep pace with the operations of the mind; Mechanical Arithmetic alone would have a tendency to reduce the mental aptitude and efficiency of the pupil. A well-balanced combination of the three, however, would be productive of the greatest development, permit mental exercise without strain and manual training without waste, besides opening up new fields of thought, investigation and practice.
While it is true that in all complex processes of calculation there are mental efforts, manual labors and mechanical appliances, if the use of pen or pencil may be included in this broad classification, we can properly distinguish the three branches of Arithmetic, according to the predominating elements. Under the name of Mental Arithmetic we may include all arithmetical operations in which the mind performs the largest part of the work, even if the pen or pencil or machine is employed to make a note of the example or register the result. We can properly classify under the head of Manual Arithmetic all processes of computation, which to a great extent depend in their execution on the hands, even if a considerable portion of the work is performed mentally. We will appropriately designate as Mechanical Arithmetic all operations in which mechanical appliances are more fully utilized, though the head is needed to direct the movements of the hand. As a matter of fact, the three Ms are so closely related to each other, and can be so intimately combined, that it is practically impossible to draw the dividing lines with any degree of accuracy, that is to state absolutely where Mental Arithmetic ceases, Manual Arithmetic, commences or Mechanical Arithmetic springs into play.
- 14 - `EXPLANATORY.
THERE is perhaps no other branch of human knowledge of equally great importance and utility, which has received so little practical consideration on the part of accountants, educators and scientists as that relating to Mechanical Arithmetic in general and computing machines in particular. Men who are rated "high" in Dun's and Bradstreet's, and women who have mastered the Odyssey in Greek, betray an ignorance in this direction which is simply appalling. And, as is usual in such cases, opinions and judgments are continually expressed with so much energy and self-confidence that they would prove positively convincing, if they were not so terribly unreasonable and lamentably ridiculous. Otherwise intelligent persons regard computing devices as useless toys, some base their judgment on primitive counters and permit it to cover the entire field of mechanical computation, others are afraid that it might enter the school room or business office, and throw teachers and bookkeepers out of employment. To remove a considerable amount of this lack of information and plenty of prejudice is a part of the mission of this work, and to begin with, an explanation of the terms used will prove useful and instructive. Mechanical Arithmetic forms that part of applied mathematics which teaches the use of mechanical appliances for calculating purposes, as well as the scientific principles underlying their practical application. Arithmo-Mechanics, on the other hand, as with the mechanical principles employed in the construction of computing devices, and embraces in its scope the study of the various appliances used and intended for arithmetical operations. To illustrate: The investigation of the different kinds of carrying mechanism, the arrangement of wheels, levers, etc., evidently pertains to Arithmo-Mechanics, while the invention of the Double Complemental Scales, for instance, greatly simplifying mechanical subtraction and - 15 - division, and to which we lay particular claim, is properly treated under the head of Mechanical Arithmetic.
The word "Arithmetic" is derived from the Latin: "Ars Metrica," which means "Metric Art." Arithmetic, the art of computation, is the most elementary branch of Mathematics. The use of the word appears first in the Sixteenth century. The art of using Arabic numerals was originally called in English Algorism, or contracted, Augrim, from the Arabic, Al-Khowarazmi which stands for the native of Khwarazm (Khiva), a surname given to Abu Ja'far Mohammed Ben Musa, an Arabian mathematician of considerable renown, who lived in the Ninth century. His work on Algebra (derived from the Arabic: Al-jebr wa'l muqabala, which means: Consolidation and comparison,) first translated into Latin in the early part of the Thirteenth century, was the source from which Europe derived the knowledge of the Arabic numerals. His surname, expressed in the Latin paraphrase as Algoritmi, came to be applied to Arithmetic, in much the same way that "Euclid" was employed to signify Geometry.
"Mechanics," the theory of machines and motors under the influences of forces and restraints, and "mechanical," pertaining to machinery, are both derived from the Latin, Mechanicus, which means, belonging to contrivances.
The terms "Arithmachine" and "Arithmachinist" are entirely new, and have been coined by ourselves to fit the importance and requirements of the occasion. They are compound words, the meanings of which are easily understood and explained. The first part is formed by the root found in "Arithmetic," and the second, "Machine," is derived from the Latin, Machina, a device or contrivance. The word "Machinist", denotes one who tends, works or operates a machine. Altogether the combinations are characterized by what constitutes a "good name," brevity, simplicity and expressiveness. In the mouths of many they have become natural, every-day expressions, and some would even be surprised to learn that as yet they cannot be found in any dictionary, no matter how elaborate and complete. Will dictionary compilers take this gentle hint? These terms are also easily translated into any of the civilized foreign languages without material change in their orthography or pronunciation, which is an important advantage, when the successful introduction of the Arithmachine in foreign countries is taken into consideration.
The selection of these names appears particularly desirable, on account of the fact that the middle M is contained in both words making up the combinations, forming a very smooth and flowing connection.
- 16 -HISTORICAL.

ERE we possessed of the necessary comprehensive knowledge and ability to give a detailed and complete description of the countless mechanical contrivances, which since times immemorial have been designed and employed by man (or woman) for calculating purposes, time and interest would be lacking with others. We will, therefore, confine ourselves to a brief review or history of the development of Mechanical Arithmetic from the earliest ages to our own times, and by so doing record one of the most interesting chapters of human progress.
The oldest and in some respects most complex "mechanical" means used for calculating purposes are the human hands. The nations of antiquity, the savages in distant lands, the child in the nursery, and even the expert accountant of today employs the fingers to a greater or lesser extent in order to facilitate and assist mental computation. In fact it is a serious mistake to suppose that mental arithmetic preceded Mechanical Arithmetic. The first ideas of numbers were unquestionably derived from material objects around us, and the first calculations must necessarily have been performed with mechanical assistance. "Pebbles in chests, beads on strings," as a well-known writer on bookkeeping puts it, were the foundation of the accounting systems of the world.
When we investigate the different mechanical appliances which in different ages and by different peoples have been employed to perform arithmetical operations, We must remember that here as well as in other branches of human endeavor "history always repeats itself." And in making the statement we do not intend for a moment to convey the idea that the most advanced inventions of to-day were known by the ancients, but simply that the human race in different stages of civilization, - 17 - as well as civilized man in different periods of his life, passes with varying rapidity through similar conditions and experiences. To illustrate: The methods of computation employed by the nations of the middle ages, even of those who laid claim to some cultivation, the methods of calculation practiced by the barbarians of to-day, the methods of accounting made use of by the ignorant in our midst, as well as tie first attempts at arithmetic by infants and young children, bear a close resemblance. There is the same limitation in mental comprehension, the same lack of adjustment of means to ends, the same difficulty in arriving at results. The bookkeeper who was pronounced by his employer the "most remarkable adder," because he could perform the same addition ten times in succession and, arrive at a different result every time, is a striking case in point.
The first computing device of which history makes any record was the "Abax," [or Sand Table] a smooth board, surrounded by a raised border or ledge, upon which the Greek schoolboys and accountants drew their diagrams and made their computations. Its name is derived from the first three letters of the Greek alphabet, Α, Β, Γ. For writing it was covered with sand, upon which marks were made with a stylus. This is the mensa pythagorea of classic authors. For arithmetical calculations the board was used without sand, and contained the counters, which were arranged thereon in parallel rows, representing respectively units, tens, hundreds, etc. About 600 B. C. Solon refers to the denominations of the several lines in a metaphor, comparing the various grades of society to the values of the counters in the different rows. The counters were coins, beans or pebbles.
Arithmetic found its first development in India, but also the Phoenicians occupied themselves with it at an early date. However, the name "Arithmetic" was given in antiquity principally to investigations of the forms of numbers, prime numbers, etc., while the science of reckoning or computation was called logistic. The difficulty of computation was greatly increased by the clumsiness of the Greek and Roman systems of notation, which furnished one of the principal causes for the adoption of mechanical devices, while those who could perform the four species of arithmetic were already - 18 - regarded as "Mathematicians." The great obstacle of a cumbersome system of notation may be realized in the fact that Archimedes (287-212 B. C.) was unable to express or establish a more accurate ratio of the circumference and diameter of a circle than 22/7 or 223/71.* [See Archimedes' Measurement of a Circle.]
* Ludolf van Ceulen (1539-1610) [See Ludolph van Ceulen] computed it to 35. Joh. M. Z. Dase (1824-1861) [See Zacharias Dase], the noted German Lightning Calculator; to 200, and Prof. Richter of Elbing to 500 places [See Archiv der Mathematik und Physik #25, 1855], viz.: 3.1415926535897932384626433832795028841971 . . . . . too numerous to mention.
The Greeks employed the first nine letters of the Alphabet as the nine significant figures of the decimal system, the second nine letters for tens, and the last letters for hundreds. Larger numbers were expressed by repetition or with the assistance of the initials of the words: Pente, Deka, Hekaton, Chilioi and Myrioi for 5, 10, 100, 1000 and 10000. Later on multiples were also indicated by placing signs over or under the figures written.
| M | C | X | I |
|---|---|---|---|
| IV | I | II | |
| IV | I | III | |
| IX | |||
| III | I | ||
| IV | IX | VI |
The Romans used the Capital letters I for 1, V for 5, X for 10, L
for 50, C for 100 and D for 500; and by placing a lower number to the
left of a higher a negative meaning was given to the former. Thus
the year of the invention of the Arithmachine would be expressed as
MDCCCXCVLII. Larger numbers were indicated as follows: 5000,
IↃↃ; 10000, CCIↃↃ; 50000, CCIↃↃↃ; 100000, CCCIↃↃↃ; 1000000,
CCCIↃↃↃↃ. In the early centuries of the middle ages the Roman
notation was considerably simplified by the
utilization of columnar rulings, indicating the
relation by placing numbers at the top. Not
only addition, but also the other species of
arithmetic were performed in an analogous
manner. The use of the cipher was still unknown,
and the corresponding places were left
vacant, resembling our modern mechanical
notation, in which ciphers are also practically
ignored. The Roman notation is now employed
on clocks and watches, monumental inscriptions,
for numbering volumes and marking
objects with brush or chisel; therefore a
knowledge of it remains both interesting and useful.
The science of arithmetic is supposed to have been introduced from Egypt into Greece by Thales [Thales of Miletus], about 600 B. C. The only mathematicians of antiquity whose writings have been preserved are Euclid [Euclid], who lived at Alexandria about 300 B. C., and who treats of arithmetic in the 7th, 8th, 9th and 10th book of his Elements, altogether consisting of thirteen books, which are principally devoted to geometry; and Diophantos [Diophantus], who also lived at Alexandria, probably in the fourth century B. C. [actually 3rd century A.D.], and whose chief work is Arithmetica. From the first century B. C. [actually first century A.D.] we have Nikomachos' books on - 19 - arithmetic [Nicomachus], devoted largely to the forms and properties of numbers. In the sixth century Anicius Manlius Severinus Boethius (475-524 A. C.) [Boethius], a Roman philosopher, wrote two books on arithmetical subjects. The Hindus, particularly excelled in arithmetic and algebra, and their best known writers were Aryabhatta (about 500 A. C.) [Aryabhata], Brahmegupta (about 600 A. C.) [Brahmagupta], and Bascara Acharya (about 1150 A. C.) [Bhāskara II]. The so-called Arabic Notation was known in Hindostan as early as the sixth century, and was introduced into Arabia about 900 A. C.
The mathematical sciences flourished among the Arabs, and from them, partly through the aid of Jewish scholars, they were carried into the European countries, surrounding the Mediterranean.
Among the most noted Arabic mathematicians were Abu Ja'far Mohammed ben Musa (died 820 A. C.) [850 A.D., Muhammad ibn Musa al-Khwarizmi]; Thabit ben Korrah, also in the ninth century [Thābit ibn Qurra]; Omar ben Ibraham (died 1123 A.C.) [Omar Khayyam] and Ibn al Haim (died 1412 A.C.) [actually fl.c. 1213, Ibn al-Ha'im al-Ishbili] Some of these wrote algebraical books in verses. In Geometry the Arabs followed the Greeks. Al Bettani [Al Battani] introduced in 912 A. C., the use of sines instead of chords, which greatly simplified trigonometrical operations; Ibn Sinan (died 946 A. C.) [Ibrahim ibn Sinan] investigated the properties of conic sections; Hassan Ibn al Haitham (died 1038 A. C.) [Ibn al-Haytham], earned the by-name "Euclid of Arabia," Abulkasim Ali Ibn Afla (died 1140 A. C.) [Jabir ibn Aflah], wrote a commentary of the trigonometry of Ptolemy [Ptolemy] (the Alexandrian astronomer of the second century, whose mathematical work "Syntaxis" was called by the Arabs Almagest); and the Persian Nasurredin (died 1273 A. C.) [Nasir al-Din al-Tusi], undertook a complete Arabic translation of Euclid, which is still in existence. Jewish scientists partly preserved their mathematical knowledge in the collective work called the Talmud, composed of the Mishna and Gemara, which were compiled between the first century B. C., and the sixth century A. C. Later writers of special renown are Salomon ben Isaac, (1040-1105) also called Rashi [Rashi]; Moses ben Maimun, (1135-1204) also called Maimonides or Rambam (Ar. Abu Amram Musa ben Maimun Obaid Allah) [Maimonides], David Gans (about 1540 A. C.) [David Gans], Simicho Luzzato (1600-1650) [Simcha Luzzatto (1583–1663) ?], and others, scattered through Spain, France, Holland, Germany, Italy and Greece, and whose mathematical - 20 - investigations form a part of the development of the countries in which they found a home.
The Roman "abacus"
[Roman abacus]
is shown in the accompanying
illustration. It consisted of a board upon
 which were fixed a number of rods carrying movable beads. There were
four beads on the long
rods and one bead on each
of the short rods opposite.
The still shorter rods to
the right were used to ex-,
press fractions. The beads
on the long rods, marked
O, indicated ounces; I,
units; X, tens; C, hundreds etc., and those on the short rods at the top five
times these quantities. Before beginning a computation
all beads were placed at the nearer end of the rods, and
numbers were represented by moving the beads to the
opposite ends of corresponding rods. Several varieties
of instruments are represented on the ancient monuments.
The Latin "calculus," from which we derive
our word "calculate," was the diminutive of calx, a
stone, and referred to the pebbles which formed the
counters of the abacus.
which were fixed a number of rods carrying movable beads. There were
four beads on the long
rods and one bead on each
of the short rods opposite.
The still shorter rods to
the right were used to ex-,
press fractions. The beads
on the long rods, marked
O, indicated ounces; I,
units; X, tens; C, hundreds etc., and those on the short rods at the top five
times these quantities. Before beginning a computation
all beads were placed at the nearer end of the rods, and
numbers were represented by moving the beads to the
opposite ends of corresponding rods. Several varieties
of instruments are represented on the ancient monuments.
The Latin "calculus," from which we derive
our word "calculate," was the diminutive of calx, a
stone, and referred to the pebbles which formed the
counters of the abacus.
From the flat board with shifting counters arranged in
rows to a board with grooves, in which the pebbles were
 rolled, was an easy step. Afterwards, we find pellets
strung upon wires, and in this form the Chinese have
used it for ages. The origin of the Chinese abacus, or
Suan-Pan
[Suanpan],
as it is called by them, has been supposed
to be the "knotted cord"
used in China for keeping
accounts before the invention of writing, also
the mode of keeping like
Chinese Tung-tien, or perforated, coins which are
strung upon a cord.
rolled, was an easy step. Afterwards, we find pellets
strung upon wires, and in this form the Chinese have
used it for ages. The origin of the Chinese abacus, or
Suan-Pan
[Suanpan],
as it is called by them, has been supposed
to be the "knotted cord"
used in China for keeping
accounts before the invention of writing, also
the mode of keeping like
Chinese Tung-tien, or perforated, coins which are
strung upon a cord.
But not only in the "abacus," also in the writing of numbers, as well as in the system of - 21 - notation there exists a wonderful resemblance between the Romans and Chinese. The latter employ horizontal lines (-) to indicate units and upright crosses (+) to denote tens, while the former used vertical lines (I) to express units and slanting crosses (X) to represent tens. This may be accounted for by the studies of Pythagoras (582-500 B. C.) [Pythagoras], a contemporary of Confucius [Confucius], in India, and the subsequent instruction of Numa in the school founded by the sage of Samos in Crotona [Crotone], a city of Magna Graecia (Southern Italy.)
The great advance of the Hindu or Arabic system of notation consisted in giving a place value to the figures. In Sanscrit, the initial letters of the names of numbers are employed from 1 to 9. An explanation of the Arabic notation in an imperfect form, without the 0, the places being indicated by means of ruled columns, can be found in a Latin Geometry, attributed to Boethius [Boethius], who died about 524 A. C. The original zero was a dot, and the Greek letter omicron (ο) was afterwards substituted, forming our nought or cipher, a word derived from the Arabic Tsaphora, which signifies "void." The same root is found in the Latin Zephyrum (by association with Zephyrus, the west wind, poetically regarded as the gentlest of all sylvan deities), Italian Zefiro, contracted Zero. The German Ziffer, which means figure, can be traced to the same root. "Nought" in common parlance is frequently designated as "nothing," while in reality it represents something, viz., the smallest imaginable quantity. The decimal and duodecimal systems of notation were used by the Egyptians at the earliest period of their known history. The Assyrians counted by sixties as well as by hundreds.
The abacus was probably invented by the Chinese, and passed then westwardly through India and Arabia to Europe, the evidences of ancient trade in this direction being found at both ends and intermediate points. The glass bottles with Chinese inscriptions, found with Egyptian mummies, prove the existence of trade relations between those nations, previous to the founding of Athens, and somewhat undermine the myth of Pliny as to the discovery of glass by certain mariners of Phoenicia. The compass, gunpowder, the art of glazing pottery, making paper, producing felt, etc., they all - 22 - came to us from the same source, and along the same route, and so it seems that we are indebted to the Chinese for a great deal more than ruining our shirt collars.
The Oriental system of notation was introduced in Europe by the Arabs and is commonly credited to them, but should be more properly called the Indian, being derived from the Hindus, and carried by the Saracens into Spain. Gerbert of Auvergne, educated at the University of Cordova, which was founded in 968, became successively a schoolmaster at Rheims, (where he introduced the abacus, the Arabic numerals, the clock, the organ and the globe,) then Archbishop of Ravenna and finally Pope Sylvester II [Pope Sylvester II]. He was the first to use the nine digits and a cipher, of which William of Malmesbury [William of Malmesbury] said that they proved "a great blessing to the sweating calculators."
The 0 and nine digits are supposed to have been originally derived from the circle and two diameters, at right angles to each other. The crude form of every figure can be easily traced with this diagram as a foundation.
The accounts of the kings of England, before the Norman conquest, were calculated by rows of coins, disposed, as in the abacus and after the conquest an amplification of the idea was introduced, the computations being performed by the Teller, at a large table, called a Saccarium. This had a ledge around it, and was covered by black cloth ruled with chequer lines, from which the word exchequer, as applied to English national finances, is derived. The first bar advanced by dozens (pence), the second by scores (shillings), the higher denominations by tens (pounds). The accounts of merchants were kept in Roman numerals until the close of the sixteenth century, and the use of the abacus remained a branch of popular education. Offices for changing money came to be indicated by a chequer-board, and the sign was afterwards appropriated by innkeepers, showing that people met at such places to settle accounts, a friendly drink being a tribute to "mine host."
The tally system as introduced in England with the Norman conquest, (1066) not for calculating, but for keeping accounts. The name is derived from the French tailler, to cut the tally-sticks, being cut and notched with a knife, small notches representing pence; - 23 - larger ones, shillings; still larger ones pounds. The stick was then split longitudinally, so as to exhibit the marks on each portion; one part was laid away in the strong room, the other was given to the creditor of the government. When the person called for payment his portion of the stick was laid against that in possession of the exchequer, and if they tallied the claim was paid. A safer method of "proving accounts" can hardly be imagined, and compared with it our modern facilities of fraud, such as chemical ink erasers, loose sales sheets, etc., are in painful contrast. This system survived the introduction of Arabic numerals into England about 670 years. In 1834, the pile of sticks in companies, regiments and brigades that had accumulated was something terrific, and a stove in the House of Lords was selected as a proper place for the cremation of this relic of the past. Unfortunately the chamber caught fire at this occasion, and, communicating it to the House of Commons, both were burned to the ground.
A translation of Ptolemy [Ptolemy], published in Spain in 1136, used the Hindu notation, and Hindu numerals, or the Arabic figures, as they are called, were introduced in Italy by Leonardo da Pisa, born at Pisa in 1175, who studied mathematics in the Orient, and was the first to apply algebraical formulas to geometrical demonstrations. His real name was Leonardo Bonacci, more frequently known as Fibonacci (filius Bonacci) [Fibonacci]. His treatise, entitled "Algebra et Almuchabala," somewhat resembles the older work of Al-Khowarazmi [Muhammad ibn Musa al-Khwarizmi], who obtained the Hindu figures from India or Afghanistan. In his "Liber Abaci," published in 1202, he explains the idea of place value in the Arabic notation. Arabic figures, though widely differing in form, can be found in writings of the eleventh and twelfth centuries; they were introduced into England in 1253 and employed by Italian merchants in the thirteenth century. But they are seldom met with in scientific works even in the fourteenth and fifteenth centuries (another instance of educational lethargy), and did not become generally known before the 16th century.
The banca of the Italian money-changers of the thirteenth, fourteenth and fifteenth centuries contained an arrangement similar to the abacus, and from this table, - 24 - which was also supplied with a money scale and test stone, our modern financial institutions derive the name.
With the improvement in the system of notation the science of Arithmetic underwent considerable development. John de Sacro-Bosco (who died in 1226) [actually 1256, Johannes de Sacrobosco], wrote Algorithmus seu Arithmeticae introductio, and his contemporary Jordanus Nemorarius [Jordanus de Nemore] compiled an extensive work on arithmetic, which was printed in 1514 in Gothic type. In the fifteenth century Lucas Paccioli dal Borgo San Sepolcro [Luca Pacioli] wrote a book, treating of arithmetic and geometry; and in the sixteenth century we find the highly esteemed classical work of Adam Reese [Adam Ries], who carried through proportions with the assistance of straight lines. The chain-rule and partnership calculations were taught in that century, the latter by Petrus Apianus [Petrus Apianus], between 1527 and 1540. The labors of Purbach [Georg von Peuerbach], Mueller [Regiomontanus], Stifel [Michael Stifel] and Duerer [Albrecht Dürer] in Germany; of Ramée [Petrus Ramus] and Vieta [François Viète] in France; and Tartaglia [Niccolò Fontana Tartaglia], Bombelli [Rafael Bombelli], Cardano [Gerolamo Cardano], Ferro [Scipione del Ferro] and Ferrari [Lodovico Ferrari] of Italy, the latter particularly in the sphere of higher equations, fall also into this period.
Decimal fractions were first employed by the celebrated mathematician Simon Stevinus [Simon Stevin], of Bruges, Belgium, in 1585, but their beautiful simplicity was obscured by the cumbersome notation he adopted. Thus, for the number 258.367 Stevinus would have written 258 (0) 3 (1) 6 (2) 7 (3), the small encircled figures indicating the number of ciphers following the figure 1 in the denominator of the equivalent common fraction. John Napier [John Napier], the famous mathematician, born at Merchiston, near Edinburgh, and a contemporary of Stevinus, recognized the importance of decimals and at the same time the absolute necessity of reducing their notation to a more practicable form. An example of their use in division was expressed by him in the following form:
861,094
————
432
and the quotient, 1993, 2' 7'' 3'''; but in a subsequent work he employs the decimal point systematically and fully defends its use. The decimal point appears to have been used by Napier in his "Constructio," in 1619, while the idea of writing it above the line is credited to Newton. Yet considerable time elapsed before the - 25 - decimal point was generally adopted. In medieval Europe a unit was divided into twelve or sixty equal parts, the first being derived from the Romans and the second from the Babylonians, and this use of duodecimal and sexagesimal fractions, of which there are still traces found in our weights and measures, diverted the attention of mathematicians from the discovery and adoption of decimals.
In algebra the use of exponents was also unknown. Harriet [Thomas Harriot], in 1631, simply repeats the letter, expressing x3, simply as xxx. Herigone [Pierre Hérigone], in 1634, used figures after the, letter, x2 for x2. Descartes [René Descartes] first introduced the modern forms, but to Newton [Isaac Newton] belongs the credit of having fully understood the importance of exponents, which led to his celebrated Binomial theorem. Mathematical writers of the 16th century employed a variety of methods for indicating radicals or roots, and their modern notation was not introduced before 1633.
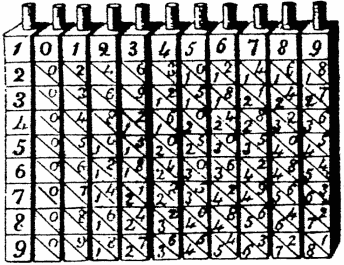
In 1614 Napier [John Napier] published the first account of his great invention of logarithms, in the "Mirifici Logarithmorum canonis descriptio," and also explained their use in trigonometry. To Napier is also attributed the invention of a contrivance, known as Napier's Bones [Napier's Bones], described in his "Rabdalogia" in 1617, but in fact first mentioned in the arithmetic of Oronce Finée [Oronce Finé] in 1532, and intended to facilitate multiplication and division for those who do not have perfect command over the multiplication table. It consists of a number of rods made of bone or other material, the face of each of which is divided into nine little squares, and each square excepting those at the top, further subdivided by a diagonal line into two triangles. These little squares contain the successive multiplies of the number in the first, the figures in the tens and units places being separated by the diagonal lines. There is also an index-rod, shown to the left, the squares of which are not subdivided. To multiply 789 by 6, for - 26 - instance, place three of the rods together so that the top numbers form the multiplicand, then look on the index rod for 6, the multiplier, and on the corresponding compartments of the three rods the following figures will be found ranged into two lines to distinguish units and tens:
| 284 | ||
|---|---|---|
| 445 | which added together | |
| ——— | ||
| give the product: | 4,734. |
Division is performed in an analogous manner.
In the seventeenth century Henry Briggs (1561-1631) [Henry Briggs], the inventor of the common system of logarithms; Vlacq [Adriaan Vlacq], the author and compiler of the first extensive trigonometrical tables; thee French mathematician, Pierre de Fermat (1601-1665) [Pierre de Fermat], who occupied himself with investigations of the peculiarities of numbers, as well as Kepler [Johannes Kepler], Cavaleri [Bonaventura Cavalieri], Descartes [René Descartes], Wallis [John Wallis], Huygens [Christiaan Huygens] and Galilei [Galileo Galilei], are all deserving of special mention in connection with the advancement of arithmetical science.
Blaise Pascal [Blaise Pascal] in 1642, and when only 19 years old, was the first to construct a computing machine with capacity to perform addition, subtraction, multiplication and division, which formed the basis of many calculating devices of later days. It consisted of a train of wheels numbered from, 0 to 9, and geared into each other to represent units, tens, hundreds, etc., very similar to the usual registering device for gas meters, and thoroughly described in Diderot's famous "Encyclopédie" (1751-80) [Encyclopédie] .
Samuel Morland [Samuel Morland] published a treatise in 1672, in which he describes two arithmetical instruments for performing addition and subtraction. Then followed G. W. v. Leibnitz [Gottfried Wilhelm Leibniz], the inventor of the differential and integral Calculus, in 1673, Poloni [Giovanni Poleni] in 1719 and Leupold [Jacob Leupold] in 1727the latter describing in his "Theatrum Arithmetico Geometricum," his own improved computing machine and those of his predecessors.
Sir Isaac Newton (1642-1727)
[Isaac Newton],
the discoverer of the
method of fluxions, Leonhard Euler (1707-1783)
[Leonhard Euler],
a Swiss
mathematician, who became blind in his later days, and
then performed elaborate calculations mentally; and
Joseph Louis Lagrange (1736-1813)
[Joseph-Louis Lagrange],
a French mathematician whose principle works are "Mecanique Analytique" and "Theorie des fonctions analytiques" are the
- 27 -
leading lights in the arithmetical field during the
eighteenth century. In addition to these Bernouilli
[Jacob Bernoulli],
Taylor
[Brook Taylor],
Wilson
[John Wilson],
d'Alembert
[Jean le Rond d'Alembert],
Carnot
[Lazare Carnot],
Laplace
[Pierre-Simon Laplace],
Legendre
[Adrien-Marie Legendre]
and others have been active workers in different branches
of mathematics in the closing years of the eighteenth or
the first part of the a present century.

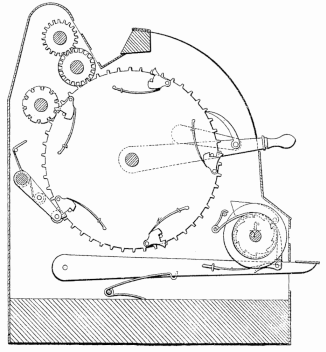
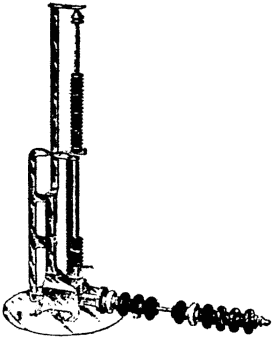
At the beginning of our century, now drawing to a close, the computing machine of the English mathematican, Charles Babbage [Charles Babbage], created quite a sensation in scientific circles. The idea of producing a machine which should perform the drudgery of arithmetical calculations first occured to him in 1812 at Cambridge, and in 1822 he completed his first model. In 1823 he began the construction of a large machine for the British government, and continued it until 1833 when operations were suspended on account of the heavy expenditures involved, which then amounted to £15,000. The finished portion, shown in the accompanying cut, is about the size of a square piano-and is still to be seen in the library of King's College, London. This renowned but unfinished machine was not intended for the execution of ordinary arithmetical operations, but particularly for the computation and printing of special tables. It is based on a peculiar arithmetical principle. The differences between the successive numbers in a table are employed to construct the table itself. For instance in a table of square (numbers: 1, 4, 9, 16, 25, 36, 49, 64, etc., the successive differences between the first and second, second and third, etc., are 3, 5, 7, 9, 11, 13, 15, etc. This series of first differences, viewed in a similar manner, presents us - 28 - with the remarkable series; 2, 2, 2, 2, 2, etc. The cubes 1 8, 27, 64, 125, 216, etc., give the first differential series, 7, 19, 37, 61, 91, etc., the second, 12, 18, 24, 30, etc., and the third, 6, 6, 6, etc., again entirely uniform in appearance. Now it is found that almost all numerical tables when thus analysed result at last in very simple series, which by addition will produce all the numbers of the required table. To accomplish this by mechanical means, Babbage constructed his Differential Calculating Engine, composed of three columns, each containing six wheels. The dials bear the figures 0 to 9 on their edges, and revolve upon vertical axes. Toothed wheels, behind the dials, bolts, acting on these, wedges to withdraw the bolts, shoulders regulating their action, etc., make up this extraordinary assemblage of complex mechanism. The lower wheel represents units, the next tens, and so on, the last tens of thousands. On the right hand column the table to be calculated is expressed; the second is the first difference column, and the third the second difference column, by which the differences are calculated, and indicated. To give some idea of the peculiarities of Babbage's eccentric genius, it will suffice to state that he believed his machine to be endowed with almost human faculties, particularly evidenced in its carrying mechanism, through which each wheel "remembered not only when to turn," but "knew beforehand when its turn came." He also referred to the machine as "calling for a table when it needed it" and "refusing to accept the wrong table from the attendant."
Babbage's Difference Engine served in turn as model for a Swedish calculating machine, commenced by George Scheutz [Per Georg Scheutz] of Stockholm in 1837, and completed with the assistance of his son Edward in 1843. It was brought to England in 1854, received a prize at the Paris Exposition in 1855, and was afterwards bought for the Dudley Observatory, Albany, N. Y., for £1,000. The British Government authorized Donkin [Bryan Donkin] to construct a similar machine which is reported by Airy [George Biddell Airy] to have computed and stereotyped in one hour and fifteen minutes a table, the completion of which required two hours and fifty-five minutes in ordinary computation.
In the first half of the nineteeth century the science
of arithmetic has been materially advanced through the
- 29 -
labors of Abel
[Niels Henrik Abel],
Cauchy
[Augustin-Louis Cauchy],
Clebsch
[Alfred Clebsch],
Dirichlet
[Peter Gustav Lejeune Dirichlet],
Eytelwein
[Johann Albert Eytelwein],
Fourier
[Joseph Fourier],
Gauss
[Carl Friedrich Gauss],
Jacobi
[Carl Gustav Jacob Jacobi],
Laroix
[Sylvestre François Lacroix ?],
Riemann
[Bernhard Riemann],
Schloemilch
[Oscar Schlömilch],
Vega
[Jurij Vega]
and others.
The Arithmometer of Thomas of Colmar
[Charles Xavier Thomas,
Arithmometer],
Upper Alsace, was the first practical machine for computing the
four species ever produced. Though complex in its
 construction it is easily
manipulated, uniform
and durable in its operation
and readily understood. It is about
twenty-two inches long,
nine inches wide and
three inches high, weighs
about twenty-five pounds,
and is operated by means of a small crank. According
to size it gives results ranging from ten to twenty places,
and is particularly adapted for multiplying and dividing.
The working mechanism consists of a series of cogged
wheels, which are engaged by pins or stops attached to
the shifters, which are projecting buttons in slits, called
figure-grooves. To operate the machine each shifter is
set at a point in its slit, marked with the corresponding
figure of the number to be registered; and by setting the
machine and turning the crank we add or subtract the
given number as often as desired. The construction
and operation of the Thomas Arithmometer was fully
described by Reuleaux
[Franz Reuleaux]
in a manual published at Freiberg in 1862. Similar machines were constructed by
A. M. Hoart of Paris, and
by Jul. Masseur and Rudolph Dobesch of Vienna.
construction it is easily
manipulated, uniform
and durable in its operation
and readily understood. It is about
twenty-two inches long,
nine inches wide and
three inches high, weighs
about twenty-five pounds,
and is operated by means of a small crank. According
to size it gives results ranging from ten to twenty places,
and is particularly adapted for multiplying and dividing.
The working mechanism consists of a series of cogged
wheels, which are engaged by pins or stops attached to
the shifters, which are projecting buttons in slits, called
figure-grooves. To operate the machine each shifter is
set at a point in its slit, marked with the corresponding
figure of the number to be registered; and by setting the
machine and turning the crank we add or subtract the
given number as often as desired. The construction
and operation of the Thomas Arithmometer was fully
described by Reuleaux
[Franz Reuleaux]
in a manual published at Freiberg in 1862. Similar machines were constructed by
A. M. Hoart of Paris, and
by Jul. Masseur and Rudolph Dobesch of Vienna.
J. B. Alexander of Baltimore, Md., patented in
1864 [Joseph B. Alexander, US 41,898, 15 Mar 1864] a computing machine,
consisting of numbered
wheels, moved by handles,
sweeping in circular axes.
It performed the operations
of addition, subtraction,
multiplication and division,
and the results appeared in a series of slits in the case.
[Note that this and the next few calculators seem to have been
taken from the Knight's American Mechanical Dictionary's entry for Arithmometer.]
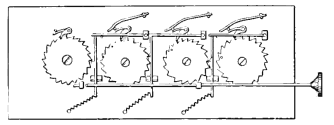
Another form was similar to the arrangement
of gas registers. The different wheels were
engaged on separate axes - and usually carried
the numbers on circular faces. A revolution of
the unit wheel gave one-tenth of a revolution to
the wheel registering tens, and so on. The numbers of
the wheels also appeared
in the opening so the slit
and were read consecutively.
Still another type of calculating mechanism was
designated as the Disk
Arithmometer, in which disks of varying diameter
overlie each other and communicate
motion to each other in regular
order, the units to the tens, the tens
to the hundreds, etc. The principle
was substantially similar to
those previously described, but the
device had a compact appearance
and the results were read from a
dial.
[This is presumably the adder made by Aaron L. Hatfield,
US 11,726, 26 Sep 1854]
Davies' Computing Machine, patented in 1867 [A. W. Davies, US 65,883, 18 Jun 1867], consisted of a number of sectional belts connecting a series of figure and master wheels. The sections of the belt were perforated so as to be moved by a peg, the selection of the place for the insertion of which being assisted by rows of numbers on the case. This device, as far as our knowledge extends, has never entered the market, no doubt on account of its primitive and deficient construction, which on the one hand caused more friction than could be easily overcome, and on the other resulted in the continuous disarrangement of the linkbelts.
Among, the better known mathematicians of the second half of the nineteenth century, who have paid special attention to arithmetical subjects, are to be - 31 - named Berger [Alexander Berger?], Cayley [Arthur Cayley], Clifford [William Kingdon Clifford], Scherk [Heinrich Scherk], Staudt [Karl Georg Christian von Staudt], Steiner [Jakob Steiner], Sturm [Friedrich Otto Rudolf Sturm], Sylvester [James Joseph Sylvester], etc.
In more recent years the invention of abbreviated and contracted methods of computation, which are specially adapted to practical requirements (Commercial Arithmetic), the compilation of an endless variety of tables for mercantile and scientific purposes (Tabular Arithmetic), the utilization of certain properties of numbers for proving accounts and verifying results (Detective Arithmetic), the application of simplified processes to statistical work, calculations connected with national debts, bond issues, etc. (Political Arithmetic), the adoption of better facilities for the instruction of the blind (Palpable Arithmetic), as well as the introduction of greatly improved and perfected mechanical appliances (Instrumental or Mechanical Arithmetic), mark the progress of a science which has hardly kept pace with human development in other directions. Among those who contributed to the various departments of arithmetical evolution, and assisted in bringing about our latter day advancement, the names of Bryant, Chapotin, Clarke, Davis, Dean, Dyrenforth, Eaton, Haines, Hansen, Jennings, Kathrein, Ladd, Lane, Myers, Olney, Packard, Preston, Robbins, Sexton, Sonndorfer, Soulé, Spitzer, Ware, etc. [I have not figured out who these people are], and last, if not least, the humble author of this work, are also worthy of record.
This brings our account practically up to the present time, in which we are confronted by a multiplicity of devices intended for calculating purposes, some mere toys, others remarkable specimens of mechanical skill and genius. And while the highest type of man has learned to employ machinery in almost every line of effort, knowing that thereby better results can be accomplished and less vital energy expended, in the field of arithmetic the vast majority still adhere and cling to the brain-racking and nerve-destroying mental methods, crudely assisted by paper, pen or pencil. Why? Partly because in some respects, in spite of our boasted civilization, we have remained barbarians, and principally because the mechanical aids, furnished up to the present time for the work of computation, have been either too cumbersome, expensive, impractical, inconvenient or unreliable, or all of these combined.
- 32 -TECHNICAL.
A CLASSIFICATION and description of the most important and distinct types of calculating appliances, either in contemporary use or at least within the reach or memory of the present generation, forms the subject matter of the following pages.
Again we take occasion to refer to the most widely
available arithmetical mechanism, the human hands.
The ten fingers, promptly and easily responding to the
impulses emanating from the brain, would indeed furnish
an ideal means of computation, if a carrying and registering
mechanism had been provided. They explain better
than all the text books the origin of the decimal system,
and are employed instinctively by young and old as
aids in simple computations. The semi-civilized Indians
of Guiana, for instance, count by the hand and its four
fingers. Thus, when they reach five, they call it a "hand."
Six is, therefore, a "hand and first finger." Ten is "two
hands;" but twenty, instead of being "four hands," is "a
man." Forty is "two men," and thus they go on by
twenties. Forty-six is expressed as "two men, hand, and first
finger."
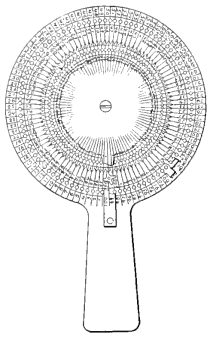
We also take once more
notice of the modern form of
the "abacus"
[Abacus],
the numeral
frame in our own elementary
instruction, a contrivance
consisting of beads or balls, strung
on wires or rods set in a frame,
and supplied with a handle.
The illustration shows the
device arranged for decimal
counting. The number indicated
by the beads on the right
hand of the frame is 198,764,
and it will be readily seen that
by transposing the beads to one
- 33 -
side or the other, as required, either addition or subtraction
may be rapidly performed.
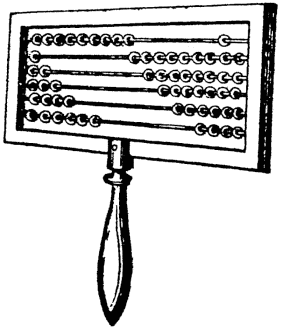
 The Stschotu of the
Russian shopkeepers, and the Suan-Pan or reckoning
board of the Chinese are more or less identical
in principle; and are both used as counters
to register the successive stages of a mental operation. The sum shown in the
annexed engraving of a
Chinese abacus is 5,196,301.
Upon each of the nine wires,
which extend across the frame,
there are seven counters, five
in the larger and two in the
smaller divisions. Each
counter in the smaller division
represents five times as much
as one upon the same wire in the larger, and the counters
are moved toward the center partition, if it is desired to
register an amount. It is employed by the wealthiest
and most intelligent Chinese merchants, who perform
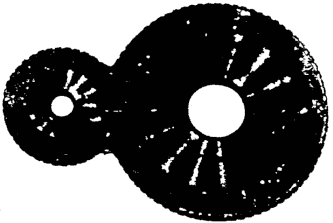
difficult calculations with amazing quickness and accuracy upon this primitive device, which only serves to demonstrate the great possibilities of arithmetical machinery, when properly developed and utilized.
The Stschotu of the
Russian shopkeepers, and the Suan-Pan or reckoning
board of the Chinese are more or less identical
in principle; and are both used as counters
to register the successive stages of a mental operation. The sum shown in the
annexed engraving of a
Chinese abacus is 5,196,301.
Upon each of the nine wires,
which extend across the frame,
there are seven counters, five
in the larger and two in the
smaller divisions. Each
counter in the smaller division
represents five times as much
as one upon the same wire in the larger, and the counters
are moved toward the center partition, if it is desired to
register an amount. It is employed by the wealthiest
and most intelligent Chinese merchants, who perform
difficult calculations with amazing quickness and accuracy upon this primitive device, which only serves to demonstrate the great possibilities of arithmetical machinery, when properly developed and utilized.
An ingenious device, somewhat related to the preceding,
is called the Lightning Adder. It consists principally
of a horizontal and perpendicular rod with buttons
on the lower rod representing units and buttons on
the upright rod representing tens.
The buttons on the perpendicular
rod are placed above the dropper
and the counting of the buttons on
the horizontal rod is always commenced at the outer end, and
when the inner end is reached, the
count is continued to the outer
end of the rod, thereby making
the unit-counting continuous. The
units buttons are moved with a
at firm push to make the dropping
of the tens automatic and certain.
The number of tens added are
read from the "vertically disposed
- 34 -
scale, and the units counted on the horizontal rod.
This contrivance excels the abacus in carrying the tens
automatically, but being only a single column adder, its
practical utility is limited.
 Next in order are the disk computing mechanisms,
the most primitive of which is known under the name of
Stephenson's or the Perfection Adding Machine
[Stephenson's Adder],
a high-sounding title, if
what the device accomplishes is considered.
It is composed of two
disks, which are decimally connected with each
other and which contain
small circular holes for
the insertion of the point of a nail or pencil. It is only
adapted for adding a single column at a time, and has a
total capacity of 200.
Next in order are the disk computing mechanisms,
the most primitive of which is known under the name of
Stephenson's or the Perfection Adding Machine
[Stephenson's Adder],
a high-sounding title, if
what the device accomplishes is considered.
It is composed of two
disks, which are decimally connected with each
other and which contain
small circular holes for
the insertion of the point of a nail or pencil. It is only
adapted for adding a single column at a time, and has a
total capacity of 200.

Another disk device, recently offered, is the Lightning
Adding Machine, so called,
consisting of a large and a small
disk, the former serving to register numbers up to 100 and
the smaller carrying the hundreds up to 2,000. It is essentially a double column machine, but its greatest objection
is the multiplicity of holes,
which is rather confusing, and
the looseness of the disks,
which do not permit of accurate and reliable manipulation.
[This might be based on the patent by Joseph W. Wright, US 451,967, 12 May 1891]
Perhaps the most
perfect of all disk devices,
from a mechanical standpoint at least, is Webb's
Adder
[Webb's Adder],
which has a capacity of three columns, is
similar in construction to
the former, but registers
the entire sum in a square
- 35 -
opening between the two revolving disks. The objection
to all disk devices is that their manipulation requires a circular movement of stylus or pencil, which is unnatural
and awkward, and the annoyance caused by the necessity of separately resetting each disk to cipher. Their
capacity is also circumscribed on account of the limitations in the practicable size of the disks.
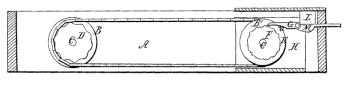
A separate and distinct class is formed by the tape contrivances, of which McClelland's Adding Ruler represents perhaps the best known example. [Robert E. McClelland, US 532,241, 8 Jan 1895],

It consists of a 15-inch ruler with a longitudinal slit, containing an endless tape with equidistant holes, corresponding to a double scale on the upper surface of the ruler, ranging from 1 to 45 and 46 to 90. The movement of the tape the entire length of the slit, about 14 inches, registers 45. Numbers between 45 and 90 require two and between 90 and 100 three movements. An opening at the right-hand end of the ruler registers the units and tens, and a hand and small circular dial the hundreds. The extreme length of the movements and the destructibility of the tapes and circular holes are its most objectonable features.

More complete in its arrangement,
but hardly better in its working
is Jewett's Calculator
[Eri F. Jewitt, US 446,753, 17 Feb 1891],
having
seven tape-bands with figures printed
thereon, which show through the
small openings at the head of the
device and indicate the result. Circular
holes and a pencil are employed
for moving the tape bands
and number scales serve as guides.
The outer case is of aluminum and
about one inch deep. The carrying
of tens is accomplished by a mental process, which sacrifices the
most important advantage to be
- 36 -
derived from the adoption of a computing machine.

Similar in results and general arrangement, though
somewhat more durable, are the bar computing devices,
so called from their utilization of returning or reciprocating
bars. The Universal Adding Machine
[George B. Fowler, US 432,266, 15 Jul 1890],
consisting
of 8 parallel bars with equidistant holes, and enclosed
in a case 4½, inches
wide and 9¼ inches long, is
probably the simplest device of the kind. A series
of number scales serve as
guides in operating this
contrivance, and the carrying is accomplished by a
straining mental process,
which directs the movement of the bars to the right or left, according to whether
the plain or the marked surface of the bar is exposed at
the point where the desired figure is to be registered.

Higher types of machines of this class are represented
by W. H. Wilson's Adding
Machine, patented July 19,
1892
[William Harmon Wilson, US 479,343, 19 Jul 1892],
in which a series of
parallel and indexed bars
are actuated by the operator
and returned by gravity;
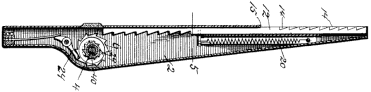 P. J. Landin's [Rapid Computer], patented, September
6, 1892, which employs
parallel bars and returning
spiral springs;
P. J. Landin's [Rapid Computer], patented, September
6, 1892, which employs
parallel bars and returning
spiral springs;
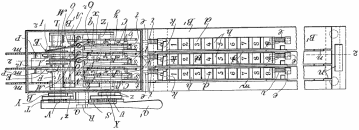 and K. E. Wiberg's, patented
March 27, 1894
[Knut Edward Wiberg, US 517,319, 27 Mar 1894],
employing
"rack plates, rocking number plates and pawls intervening between the rack plates and the number plates,
springs for giving end motion to the rack plates and a
pusher for returning the rack plates to their normal
positions, number rings
and gearing intervening
between the rack plates,
and number rings, etc."
This description, which is a part of one of the patent claims, clearly indicates a complexity of construction
- 37 -
likely to result in mechanical difficulties and arithmetical
inaccuracies. The principal defect to these machines is the characteristic feature of rebounding bars, which are
noisy, confusing and unreliable when rapidly operated, as well as the weakness and insufficiency of the carrying mechanisms.
and K. E. Wiberg's, patented
March 27, 1894
[Knut Edward Wiberg, US 517,319, 27 Mar 1894],
employing
"rack plates, rocking number plates and pawls intervening between the rack plates and the number plates,
springs for giving end motion to the rack plates and a
pusher for returning the rack plates to their normal
positions, number rings
and gearing intervening
between the rack plates,
and number rings, etc."
This description, which is a part of one of the patent claims, clearly indicates a complexity of construction
- 37 -
likely to result in mechanical difficulties and arithmetical
inaccuracies. The principal defect to these machines is the characteristic feature of rebounding bars, which are
noisy, confusing and unreliable when rapidly operated, as well as the weakness and insufficiency of the carrying mechanisms.
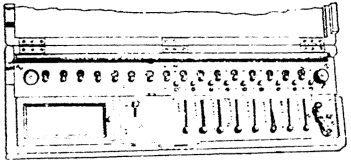
Crank machines, not those invented or operated by
cranks, but the type of computing machines, in which a
revolving crank forms an essential feature of construction
and manipulation, are particularly adapted for the
processes of multiplication and division, and in this
respect outrank any other kind of calculating instruments
yet devised. At the head of this class, considering age
and originality, stands Thomas' Arithmometer,
described and illustrated in the preceding chapter
[Charles Xavier Thomas,
Arithmometer].
To multiply, for instance, 4,562 by 394, we move the shifters
on the figure plates until they represent the multiplicand,
then the crank is turned four times for the units
figure of the multiplier, the slide is then moved one
place to the right and the
crank turned nine times
for the tens figure of the
multiplier, then the slide
is again moved one place
to the right and the crank
turned three times for the
hundreds figure of the
multiplier. In this example
the crank would be turned sixteen times, when
the product 1,797,428 could be read from the disks on the
slide. With a maximum speed of about four revolutions
per second the above example could be easily solved
on this machine in five
seconds. Practically the
same machine is made by
Tate of England
[Samuel Tate],
and A.Burkhardt of Germany
[Arthur Burkhardt],
the latter considerably
improved in workmanship
and durability and offered
- 38 -
in this country under the name, of Reckoning Machine,
enclosed in a highly finished box, and weighing
about twenty-five pounds.
 Another machine of somewhat
similar construction is the invention of Willgot,
Theophilovitch Odhner, a Russian, known in Germany
as the Brunsviga
[Brunsviga], and adopted by many governments,
scientific and leading business institutions of
Europe. The machine is simple in construction, substantially
made and compactly put together, the accompanying
illustration giving an excellent idea of its
appearance.
Another machine of somewhat
similar construction is the invention of Willgot,
Theophilovitch Odhner, a Russian, known in Germany
as the Brunsviga
[Brunsviga], and adopted by many governments,
scientific and leading business institutions of
Europe. The machine is simple in construction, substantially
made and compactly put together, the accompanying
illustration giving an excellent idea of its
appearance.
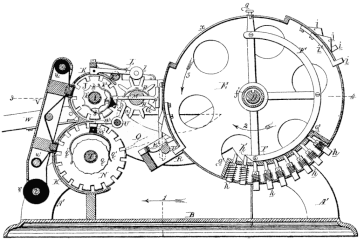
Another crank-operated computing machine is the
invention of Frank T. Baldwin
[Frank Stephen Baldwin, US 159,244, 2 Jan 1875],
of which only a very
limited number have been made. It is one of the smallest machines of this type
ever produced, and represents a most ingenious
though delicate specimen of mechanical construction, consisting of a
series of toothed typewheels combined with a
cylinder, carrying teeth,
which admit of being adjusted to revolve one or more of
said wheels. A screw shaft and locking device, whereby the cylinder may be rotated with the shaft or retained
while the shaft rotates, and disks having a frictional attachment with arms or stops, so to arrest the movement
of one or more wheels while the shaft is turning, are
some of its most characteristic features.

The best American machine of this class is the invention of George B. Grant [George Barnard Grant], who by a peculiar streak of modesty, proclaims the calculating machine as "an accumulation of ingenuity to which no one man has contributed anything of very great importance." Granting this in Grant's case and for the - 39 - sake of harmony, we still are inclined to believe that the field of calculating appliances offers as much room for the display of originality and genius as that of any other complex mechanism. It is to be hoped at least that the apparent limitations of Grant will not prove insurmountable obstacles to other inventors of computing machines. This criticism, however, does not in any way reflect upon the merits of Grant's "Ciphering Handorgan," which in its arrangement and construction, simplicity and durability excels every other machine of the same type in existence. As above referred to, while practically valueless for the processes of addition and subtraction, the crank machines are particularly adapted for multiplication and division, involution and evolution. They all require two distinct operations, that of setting the figure pins, etc., and turning the crank, in order to register a number. These machines range in price from $60 to $400.
We now approach a group of calculating instruments
which fall under the broad and somewhat indefinite classification
of key machines. And in enumerating and describing the most important members of this class we will
proceed from the simple to the more complex kinds, from
the primitive and inefficient to the most effective and
practical specimens.
In Spaulding's Adding Machine
[Cyrus Grant Spalding, US 146,407, 13 Jan 1874, and US 293,809, 19 Feb 1884],
or the "Surprise
Adder," as it has been recently
named, the keys slide horizontally towards the operator.
There is a key for each of the
nine digits and two dials, a large
one for the totals up to 100 and
a small one for the hundreds,
up to twenty. It is a single
column adder, and the inventor
suggests that "with practice
the column may be added mentally, and with the machine at
the same time, which is indeed a very poor recommendation for the machine.
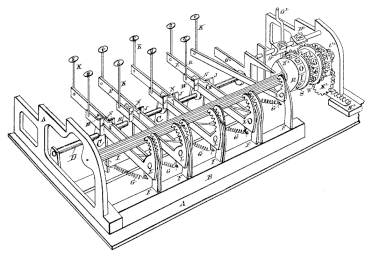
Bouchet's Adding Machine, patented March 31,
1885
[Michael Bouchet, US 314,561, 31 Mar 1885],
is another single column key machine, provided
with nine keys and three decimally connected numeral
- 40 -
wheels, which exhibit the result through an
opening in the ease. The
limit of capacity of this
machine is 999, and its
principal features are keybearing levers, curved
racks and toothed rollers,
which connect with the
numeral wheels.
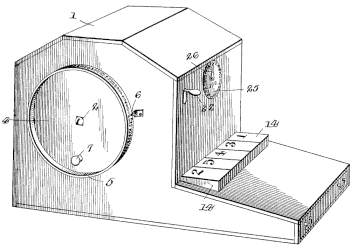
Wendt's Calculating Machine, patented July 7,
1896
[Fred Wendt, US 563,435, 7 Jul 1896],
has only five square
keys, the remaining four
figures being obtained by
striking combinations of
the other five. Totals up
to 100 are registered on
the large side wheel and
the hundreds are carried
to the small wheel in
front. The keys may be
described as piano keys,
which point to the conclusion that it was perhaps never
intended for calculating purposes.
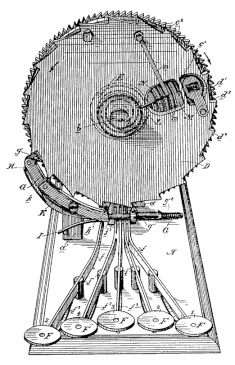
The Centigraph
[Arthur Ewing Shattuck, US 453,778, 9 Jun 1891]
is also a five-key single column
adder, somewhat resembling the Stenograph Shorthand
Machine, which has been heard
of more in former years. It contains a powerful spring which
turns the saw-like wheel a certain
distance, when released by the
striking of the keys. The totals
up to 100 are shown in the square
opening to the left, the hundreds
up to 5 are pointed at by the
hand on the dial segment. The
metal parts are nickel-plated and
the base of the machine is made
of black walnut. The machine is
eight inches long, six inches wide
and six inches high, and weighs
about two pounds; When run
down it has to be wound up
- 41 -
again, which ought to be a healthful recreation for the
office boy, and insure its adoption in dull times. It is very
difficult to speak of these machines seriously as adding or
calculating machines. They lack all the essential characteristics of such instruments, and their failure as business propositions speaks highly in favor of the sound
judgment of a discriminating public.
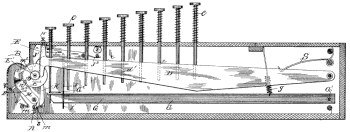
Among the key machines of larger capacity and
dimensions D. E. Felt's Comptometer
[Comptometer]
deserves a prominent place. Briefly described, it consists of a box
15 inches long, 8 inches
wide and 5 inches high,
weighing about ten
pounds. Its mechanism is composed of a
series of numeral wheels, each standing for an order of
numbers, and on the surface are arranged keys, for every
figure, of the different denominations. The eight column machine has not less than seventy-two keys, of
varying depth of depression, as shown in the accompanying illustration, which somewhat interferes with its speed
and sometimes affects its accuracy. The "nine" keys,
 for instance, must be depressed about nine times
as deep as the "one" keys,
and if in rapid operation
any depression is not fully
completed, a wrong answer
necessarily results. It is
naturally adapted for addition and subtraction,
while multiplication and
division can also be performed on this machine
by repeated addition and
subtraction. On account
of its bulk and weight it
cannot be brought close
to the figures operated on,
which either necessitates
the services of an assistant
for calling off the items, or compels the operator to keep
track of the work with one hand, to prevent omissions or
- 42 -
repetitions, leaving but one hand to manipulate the keys.
Furthermore, as every key must be struck separately
and distinctly, to prevent inaccuracies in registering and
carrying, the advantage of keys, so striking in typewriters, is rather doubtful in computing machines.
for instance, must be depressed about nine times
as deep as the "one" keys,
and if in rapid operation
any depression is not fully
completed, a wrong answer
necessarily results. It is
naturally adapted for addition and subtraction,
while multiplication and
division can also be performed on this machine
by repeated addition and
subtraction. On account
of its bulk and weight it
cannot be brought close
to the figures operated on,
which either necessitates
the services of an assistant
for calling off the items, or compels the operator to keep
track of the work with one hand, to prevent omissions or
- 42 -
repetitions, leaving but one hand to manipulate the keys.
Furthermore, as every key must be struck separately
and distinctly, to prevent inaccuracies in registering and
carrying, the advantage of keys, so striking in typewriters, is rather doubtful in computing machines.
The Comptograph is essentially a Comptometer with a
listing or typewriting attachment, recording the amounts
 registered on a paper roll. For reasons best known to
the manufacturers this machine has never entered the
field as a competitor of Burroughs' Registering Accountant
[Burroughs],
the most successful listing machine
on the market at the
present time. Owing to
its great cost, size, weight,
etc., its adoption has
been confined to the
largest business and
financial institutions. It
has found particular
favor in the leading
metropolitan banks, for
the special purpose of
preparing check-lists for
the clearing house. Its speed is greatly impeded by the
double operation of depressing the keys and turning the
printing lever, which is necessary to record an amount.
The accompanying cut gives a fair idea of its appearance.
There are about 1,200 parts in this machine, some exposed to view through the plate glass panels in the sides.
Its even and uniform stroke, and the opportunity to verify
and correct the amount last registered, before making
the printed record, are its most desirable features.
registered on a paper roll. For reasons best known to
the manufacturers this machine has never entered the
field as a competitor of Burroughs' Registering Accountant
[Burroughs],
the most successful listing machine
on the market at the
present time. Owing to
its great cost, size, weight,
etc., its adoption has
been confined to the
largest business and
financial institutions. It
has found particular
favor in the leading
metropolitan banks, for
the special purpose of
preparing check-lists for
the clearing house. Its speed is greatly impeded by the
double operation of depressing the keys and turning the
printing lever, which is necessary to record an amount.
The accompanying cut gives a fair idea of its appearance.
There are about 1,200 parts in this machine, some exposed to view through the plate glass panels in the sides.
Its even and uniform stroke, and the opportunity to verify
and correct the amount last registered, before making
the printed record, are its most desirable features.
Another machine of this kind is W. W. Hopkins' Adding, Subtracting and Recording Machine, patented March 27 1894 [William Wallace Hopkins, US 517,383, 27 Mar 1894], which, however, has, as yet not been offered to the public. In it the number of keys are reuced to nine, the record of the various denominations being effected by an automatic shifting mechanism. It is briefly described by the inventor as: "An adding machine having a series of registering mechanisms, one of each numerical order, printing devices recording the numbers registered, a motor impelling these registering - 43 - mechanisms and printing devices, a carriage determining the numerical order in which the machine is working and keys controlling said motor and carriage." Some idea of the complexity of the machine will be formed by inspecting the patent application, which is composed of not less than fourteen sheets of drawings and forty pages of closely printed matter.
The objectionable feature
of the large key machines
is principally the mental confusion caused by a multiplicity of keys, requiring considerable practice and dexterity in their manipulation, which difficulty is greatly
increased in some by a hard, noisy and uneven stroke.
They are also unsuited for the regular routine work of
accountants or bookkeepers, being too large and clumsy
to be brought in close proximity with the work. Besides
the practical utility of listing machines is limited, over
90 per cent of the calculations required in business offices
which a practical computing machine ought to facilitate, making a listing attachment absolutely superfluous.

In conclusion we wish to briefly describe a few devices,
which, while partaking of some of the features of computing machines, are in reality nothing else but tabular
arrangements with mechanical improvements. At the
head of this class, considering its complexity and scope,
stands Thatcher's Calculating Instrument
[Edwin Thacher, US 249,117, 1 Nov 1881],
consisting of
a cylinder 18 inches long and 4 inches in diameter, revolving within a framework of
triangular bars. The scales,
the longest ever made,
contain upwards of 33,000
divisions and 17,000 engraved figures, executed by
W. J. Stanley of London, England, upon a dividing machine made expressly for this instrument. Examples in
multiplication, division, proportion, powers or roots are
- 44 -
solved, usually by a single operation, and results can be
obtained accurately up to the fifth place.

Fuller's Spiral Slide Rule [George Fuller, US 219,246, 2 Sep 1879], is another device of this kind. A single logarithmic scale, 42 feet long, is wound spirally around a wooden cylinder, which can be moved up or around a wooden axis held by a handle. Simpler contrivances of a similar nature are Thompson's Lumber Calculator, indicating the number of cubic feet in the most frequently occurring dimensions of lumber; and F. J. Smith's Multiplying Machine, containing a table of multiples of the numbers from 1 to 25, arranged in cylindrical form.
Among circular tables with mechanical features Sexton's Omnimetre deserves special mention. It is a circular slide rule, for which is claimed that it requires fewer motions to solve the most intricate problems than any form of calculating instrument known. With its aid squares and cubes, square roots and cube roots can be computed, as well- as trigonometrical problems solved.
The utility of slide rules is limited, owing to the fact that they are not adapted for addition and subtraction, and solve other problems only to four or five places. The vast assembly of minute figures crowded into a small space is also a serious ocular objection, productive of mistakes and inaccuracies.
The limitations of this work compel us to exclude from this condensed presentation numberless counting and tallying devices, cash and fare registers, computing scales, etc., which all perform one or the other of the functions of calculating machines, and to confine ourselves to a description and illustration of the principal devices, exclusively employed for calculating purposes. We reserve for the following chapters a more elaborate account of the Arithmachine, its scope, construction and manipulation, believing it not only to combine all the desirable qualities of other computing devices, and to be free from their most objectionable features, but to possess many new, original and important points, which ought to insure its adoption by progressive accountants, business men, educators and scientists everywhere.
- 45 -
Capacity, 999,999.99.

Actual Size.
ARITHMETICAL.
With a firm faith in the educational importance and practical utility of Mechanical Arithmetic, and the positive conviction that a computing machine, answering the every-day requirements of the office or counting-room, had as yet not made its appearance the labors of developing and perfecting the Arithmachine were carried on; until at last the finished and completed product is within everybody's reach. And while we do not claim for it absolute perfection, and are ready to grant that further investigations and increased facilities of manufacture will enable us to make other valuable improvements, we still believe that we have come nearer to what a really practical computing machine ought to be than any of our predecessors in the same field of human effort. And this is quite natural. Inventions are but stepping stones to greater achievements, and it is a good deal easier to avoid the errors of the past than to foresee the possibilities of the future.
In constructing the Arithmachine the following indispensable characteristics of a practical computing machine were continually borne in mind:
- Simplicity. No Philadelphia lawyer should be required to fathom its mysteries.
- Rapidity. Limited practice should enable anyone to operate it quickly.
- Accuracy. The results arrived at should be absolutely reliable.
- Durability. No mechanical skill should be necessary to keep it in good working order.
- Lightness. It should be easily moved over a column or carried in the pocket.
- Smallness. It should compare in size with the often missing phrenological bump of the mental calculator. - 47 -
- Noiselessness. The modern counting-room is already overburdened with unavoidable noises.
- Convenience. It should act as a guide to the figures operated on.
- Capacity. It should carry any, desired number of columns simultaneously.
- Cheapness. It should be within easy reach of everybody who has use for it, the presumption that bookkeepers are capitalists being sometimes unfounded.
The arithmetical features of the Arithmachine, which cannot be found in any other computing machine known, and greatly facilitate its manipulation, are:
- The arrangement of the operating surface, which closely resembles a blank book ruling, and makes the placing of figures natural and easy.
- The introduction of distinguishable partitions, which greatly assists the eye in distinguishing the different columns.
- The invention of the double complemental scales, which simplifies the instructions for subtraction and division and at the same time relieves the eyes considerably.
- The disposition of the indicator opening at the head of the machine, practically out of sight when operating it, and at an angle most convenient for reading the results.
- The utilization of chain covers to prevent the actuation of certain chains and to interrupt the decimal connection of the numeral wheels to any desirable extent, which is of material assistance in computations with fractions or denominate quantities.
- The adoption of a removable stop, which aids considerably when the repeated placing of a series of numbers in the same row is desired, having also the effect of reducing the operating surface.
- The attachment of a movable decimal point, as an aid in numerous computations, particularly division, by pointing off results and indicating the figures last considered.
- The distribution of sliding shutters, which effect the hiding from view of any desired figure in the indicator opening, most beneficial in subtraction and division. - 48 -
- The position of the resetting wheel on the right hand side of the machine, closely fitting to the case, and effecting the return of ciphers in the indicator opening, by means of a single movement.
- The insertion of an erasable tablet, which will be found a great convenience in making memoranda of examples or results, being always on hand, and nearest to the indicator opening.
But not only in certain material features of the Arithmachine do we claim superiority over other computing machines, also in the methods of utilizing it have we made great strides forward from the crude and antiquated, instructions, now commonly practiced by the users of arithmetical appliances.
In Addition the method of grouping amounts as applied to the Arithmachine, and which can be easily practiced, as the eye is guided by the machine itself in considering the items next to be placed on the chain-board, will prove a time and labor-saving improvement of considerable value. In Subtraction the introduction of the double complemental scales greatly simplifies the rules to be observed in connection with this process and eliminates the mental feature, which complicates mechanical subtraction on other computing machines. Multiplication on the Arithmachine is a natural and easy operation, the mind performing those mechanical processes for which it is best adapted, and the machine co-operating simultaneously, which gives more satisfactory results and requires less effort than the machine methods previously employed. Division is greatly simplified as a natural consequence of the improved processes employed for subtraction and multiplication, it being in reality nothing but a combination of the two.
Calculations with fractions are easily performed on the Arithmachine, by making use of the chain-covers and reserving the two right-hand columns for fractional items; and denominate quantities offer no difficulty, if the instructions regarding the use of the chain-covers and shutters are carefully observed. Incidentally we may state that the above-named attachments, which have never before been utilized in connection with, any computing machine are almost indispensable assistants in certain operations and materially increase the general practicability of the Arithmachine.
- 49 -The compilation of powers and extraction of roots can be accomplished on the Arithmachine by means of simple and advanced methods, which, with a limited amount of study and practice, will present little difficulty to the ambitious arithmachinist.
The Arithmachine also lends itself to the execution of combined processes, such as: Balancing accounts, computing interest, averaging dates, etc., and can also be advantageously employed in conjunction with interest, discount, exchange, etc., tables, as a means of registering the partial results, and arriving at the final answer.
A new principle, not previously dwelt upon in Mechanical Arithmetic, though practically invaluable, consists in utilizing the right-hand columns of the machine for the placing of amounts in calculations where the tendency of the process is towards increase, as for instance: Addition, multiplication, involution, etc.; and the left-hand columns for registering the amounts in computations which have a tendency towards decrease, such as subtraction, division, evolution, etc. The object is obvious. In the first class of problems places are left to the left of the given items, to permit of arriving at the larger result, while in the second class places are left to the right to allow the annexing of ciphers or the computing of additional places of the result. The carrying out of this principle in subtraction has the additional advantage of eliminating the figures in the highest place, which have no bearing the result, but are the natural consequence of the complemental method. The only exception in the application of this principle is the desirability of leaving in division and evolution a place to the left of the registered amounts for the accommodation of the first quotient and root figures. The placing of amounts in the left-hand column of the Arithmachine need not cause the least confusion, especially as the decimal point or digit shutter can be utilized to mark the lower places of an item, ending in ciphers. The relation of the places being decimal (unless changed by the insertion of chain covers), it makes little difference, as far as reading the items is concerned, whether they are placed at the left or right side of the indicator. In fact, it is comparatively easier to register to the left than to - 50 - the right, as no notice need be taken of how many places are required to accommodate all the figures of a given amount.
In many instances problems can be solved on the Arithmachine according to accustomed methods, and the knowledge of mental and manual arithmetic one possesses can frequently be utilized in conjunction with the machine. The Arithmachine can also be employed to register partial results, or to combine separate items, which otherwise would have to be first written out and then added together. In fact, we believe that only through the combined utilization of the three branches of arithmetic mental, manual and mechanical can the latter be made popular and useful and the greatest arithmetical efficiency attained. In the light of modern developments one's knowledge of arithmetic must be considered sadly deficient, if it only embraces the first two branches, and many important points of information, as well as useful methods of computation, are beyond the reach of those who do not investigate Mechanical Arithmetic and its mechanical representative, the Arithmachine.
But Mechanical Arithmetic, in order to be practicable, must be practical; it must be presented with the accountant's insight, not with the mechanic's skill alone. It must combine the natural functions of the mind and hand with those of the machine. Some processes of the mind are purely mechanical, and any effort of making them more so simply results in burdening the brain. Think of the nonsense, therefore, advocated in the instructions to one of the largest (not greatest) computing machines known, according to which the multiplication of 9 by 8, for instance, is performed by depressing the 9 key eight times, which involves: 1. the concentration of the mind on the 9 key; 2. the mental counting of eight strokes, and 3. an amount of pressure on the finger tips, resulting in nervous strain certainly in excess of that occasioned by the mento-mechanical process of reporting 9 times 8 as 72. The constructor of the machine above referred to also asserts (without any proof) that "mental and mechanical arithmetic do not mix very well." At the same time he advocates a method which in order to multiply 98 by 87, for instance, - 51 - requires thirty distinct movements of the hand and fingers each to be guided by a separate mental impulse, not to speak of the repeated counting of a certain number of depressions of separate keys in different rows, and the necessity of considering the columns in which the keys have to be struck. If mental and Mechanical Arithmetic do not mix very well, they are certainly badly mixed here. We contend, on the other hand, that the products of the multiplication table (the "Einmaleins" of the Germans) are recalled by an automatic operation of the reproductive faculty, the memory, which is more natural and mechanical than the mental counting of a certain number of depressions, and more reliable, as it abreviates entirely the errors resulting from a "mistaken count." Besides the addition of numerous ones is regarded even, by experts as the most difficult and tedious task in mental addition, as evidenced by the fact that lightning calculators, capable of arriving almost at a glance at the sum of a complex column of digits, break down completely when specially prepared columns containing an excessive number of ones are presented to them. Now, whether ones are to be added in a column of figures or by counting separate strokes, makes very little difference, as far as the mental effort is concerned. The machine has done all that should be reasonably expected of it, if it registers the results arrived at by mechanical mental processes, and if it relieves the mind of the burdensome carrying of figures, and the time consuming addition of the partial products.
In this connection it may prove quite interesting to refer to the catch question: About how long does it take to count 1,000,000? Without reflection many would consider two or three days ample time to accomplish such a comparatively easy task. But, even supposing that one could count 60 every minute, which is a rather high estimate for the larger numbers, especially if the condition of pronouncing them is imposed, and could keep it up for 8 hours every day, which would prove a rather trying occupation, considering the monotony of the work, it would still require not less than six weeks to accomplish the task. But as the actual average could probably be not more than 10 numbers a minute, about eight months would be occupied by this useless pastime. To count a billion would require about 693 years, allowing only Sundays or holidays for recreation.
The change from writing to "placing" figures in itself will prove restful to many, while the fact that the - 52 - senses of touch and sight are gently stimulated by the manipulation of the Arithmachine will be found a relief from the purely mental effort in arriving at results, dealing entirely with abstract numbers.
It is unquestionably due to the advocacy of awkward and unreasonable methods in combination with the objectionable computing mechanisms hitherto introduced, that Mechanical Arithmetic did not enter more generally as a time and labor-saving element in the countingroom, and has not met with a wider appreciation by a patiently calculating public. But it is confidently hoped that the Arithmachine and advanced mechanical methods applied to it, will disperse the prejudices commonly entertained with regard to computing machines, and give to Mechanical Arithmetic the place which it ought to occupy as a scientific study and educational factor. And if Mechanical Arithmetic has the educational and practical importance we know it to possess, it forms an essential part of the science of arithmetic and ought to be taught and studied in our schools and colleges. The knowledge of arithmetic must be considered incomplete, as long as one of its most important branches is entirely ignored, especially as in this age of mental over-pressure mechanical computation is likely to prove more beneficial than mechanical processes in any other field of human effort.
SQUARE OF DIGITS.
| 1 | 6 | 8 | 9 | 2 | 4 | 5 | 7 | 3 |
| 9 | 2 | 4 | 5 | 7 | 3 | 1 | 6 | 8 |
| 5 | 7 | 3 | 1 | 6 | 8 | 9 | 2 | 4 |
| 8 | 1 | 6 | 4 | 9 | 2 | 3 | 5 | 7 |
| 4 | 9 | 2 | 3 | 5 | 7 | 8 | 1 | 6 |
| 3 | 5 | 7 | 8 | 1 | 6 | 4 | 9 | 2 |
| 6 | 8 | 1 | 2 | 4 | 9 | 7 | 3 | 5 |
| 2 | 4 | 9 | 7 | 3 | 5 | 6 | 8 | 1 |
| 7 | 3 | 5 | 6 | 8 | 1 | 2 | 4 | 9 |
MECHANICAL.
IT is one thing to produce a calculating contrivance, and ignore every practical consideration of size, weight, shape, noise, price, etc., and quite another thing to construct a computing machine, which can be easily moved over a blank book column or carried in the vest pocket, which is conveniently shaped, rapid, accurate, reliable, durable and noiseless in its manipulation, small in size and light in weight, and within reach of all who may have use for it - qualities which characterize the Arithmachine, and cannot be found in any other Computing machine in existence.
Without dwelling on the trials and disappointments which an inventor invariably experiences in the uninteresting pursuit of "interesting capital" as it is commonly called, it is unquestionably true that a wonderful amount of enthusiasm and stick-to-it-iveness is required to battle against financial and mechanical difficulties on the one hand and the "assistance" of advising relatives, criticising friends and patronizing acquaintances on the other.
We will not attempt to offer in these pages a learned treatise on statics or dynamics, kinematics or odontics, but explain in a popular way the various mechanical problems which had to be solved, in order to make the now completed product, known as the Arithmachine, possible. And this will indirectly answer the usual question, why such a simple and practical invention has not made its appearance long ago. It is easier to admire or belittle an accomplished fact than to accomplish it. The steam engine, the telegraph, the telephone, the phonograph, etc., are all examples of inventions which, according to the opinion of the wiseacres, have been unnecessarily delayed more than a thousand years.
The first difficulty which presented itself after the - 54 - general plan of the Arithmachine had been conceived, was the construction of the chain links, which connectedly form the operating surface of the Arithmachine, and serve the double purpose of actuating the numeral wheels, while being moved themselves by the pencil stylus. A year of investigation and experiment was necessary to bring the manufacture of the chains to its present state for perfection.
Another important problem, which had to be solved satisfactorily, was the contact of the chains and numeral wheels, in order to reduce the friction to a minimum, when a number of wheels are turned simultaneously, and to prevent the disarrangement of the chain links. The utilization of the natural pressure of the stylus pencil, exerted while operating the machine, solved this problem in a simple and effective manner.
A third question of considerable moment consisted of making the depression of the chains automatic and effective, limiting it in depth and controlling it in both directions, upward and downward, at the same time arriving at a satisfactory solution of the locking problem, which prevents the accidental movement of the chains or numeral wheels, and of the alignment problem, which keeps the chain links and numeral wheels evenly arranged on the chain-board and in the indicator opening.
Next in order was the carrying problem, of vital importance in any numbering device, but particularly difficult of solution in connection with the Arithmachine, owing to the limited dimensions of the numeral wheels. The construction finally adopted answers every practical requirement, being of remarkable size and strength, considering the smallness of the wheel, and in itself a mechanical achievement of considerable importance. Associated with it is the return problem, which required much thought and study, resulting in an arrangement entirely distinct from the carrying mechanism, relieving both of mechanical strain and thereby increasing their durability.
The complete separation of the various sections of the Arithmachine, particularly to prevent friction resulting in inaccuracies, has been successfully accomplished by the introduction of distinguishable partitions, - 55 - which themselves form a part of the carrying mechanism, protect the exposed chain sections and wheel faces, serve as rests for the lever pins, roller pillars and central arbor, and in combination with the outside frame plates give the operating and registering mechanism a strength and stability which, without them, would be practically impossible.
Space does not permit us to enumerate here the many minor problems and difficulties in designing, perfecting and completing the Arithmachine, which presented themselves with a promptness and persistency as to incline one to the belief that the forces of the universe are all united in the one effort of counteracting and annoying the struggling inventor, and to delay and destroy the results of his labors and investigations.
The Arithmachine is composed of a number of perfectly identical sections, according to the number of columns provided, and the construction of each section may be properly divided into two distinct parts, which we will briefly designate as the operating and the indicating mechanism.
The operating mechanism consists of an endless chain composed of 35 uniform and peculiarly shaped links, joined so perfectly that the connections are invisible when viewed from above, and permitting the free movement of the chain. The transverse teeth, which form a part of the chain links, serve to actuate the numeral wheels when thrown in contact with them, furnish a hold for the stylus pencil when operating the chain, and also lock it by means of a bar and roller lock at the forward end of the machine. The endless chain passes in its movement over two pentagonal rollers, which reduce the friction to a possible minimum, there being absolutely no slipping of the chain links, but a simultaneous arrival and departure of a link at or from the pentagonal roller. Three of the chain links at either side of each section are at all times relatively at rest on the pentagonal roller. Between the two pentagonal rollers and on the underside of the chain-board or operating surface is a platform lever, which forms a solid foundation for the movement of the chain, with a foot at one end causing, when depressed, an immediate opening of the chain-lock, and connected with it near the other end - 56 - is a contact lever, which throws the chain in tangential contact with the numeral wheel; as soon as depressed and moved by the stylus pencil, and when at rest assists in locking the chain by preventing the turning of the adjoining pentagonal roller. A slightly curved spring presses the platform lever and chain-board upwards against the bar and roller-lock, and joined to it is a tension spring, which prevents any undesirable looseness of the chain. The bar and roller lock at the forward end of the section and a similar combination at the farther end contribute also to the uniform movement of the chain and serve at the same time to prevent friction on both sides of the chain by keeping the separating partitions equidistant.
The indicating mechanism is composed of a ratchet wheel, bearing on its faces the ten figures in raised type, and having within two circular depressions, the one containing ten circumferential ratchets, and the other the carrying and return levers and springs appropriately arranged. A ring or collar between the numeral wheel and the central arbor, serves to hold the return disks in position, and, being slightly wider than the wheel, allows it to move freely.
A resetting wheel on the outside of the case, fastened to the neck of the central arbor, and held in position by the release pin and spring; a comb spring behind the ratchet wheels, which regulates their movement and insures the alignment of the figures in the indicator opening; partitions which separate the sections, hold the lever pins in position and through a larger opening between the numeral wheels form a part of the carrying device, and two outside frame plates, which, hold the inner mechanism together and permit it to be removed from its case like a watch, complete the mechanical construction of the Arithmachine, which, including the outside parts and attachments, referred to in the "descriptive" part of this book, is composed of not less than 750 parts, or rather 440 working parts held together by 310 screws and rivets. The Arithmachine is made entirely of metal; in other words, no breakable or deteriorating wooden or rubber parts enter into its construction. Every, working part is properly strengthened and every wearing part made of steel or other suitable material, - 57 - and capable of performing, about ten times the work expected of it, which enables us to unreservedly guarantee the Arithmachine tor two years, while with proper care and usage it is likely to outlast the operator.
The demand for a practical computing machine which may be carried in the pocket is neither of recent origin, nor is it limited to any particular section of the globe. A good many years ago, when Babbage's Difference Engine created a considerable sensation in the scientific world, Count Strelitzky related that while traveling in China he was frequently questioned regarding this invention, and that Chinamen were particularly anxious to know whether it could be carried in the pocket. Mr. Babbage is reported to have resented the "insinuation" with the remark: "Tell them it is in every sense an outof-pocket Machine." Up to the present, however, this demand has been practically ignored by inventors, partly on account of the seemingly insurmountable obstacles which had to be overcome, and principally because inventors of computing machines had comparatively little experience in practical accounting work, and a corresponding lack of appreciation of actual requirements. Particularly the more efficient key-operated machines have honestly earned the title of "out-of-pocket Machines," which may be applied to them in every meaning of the phrase.
All the important features of the Arithmachine, as well as many minor details and improvements, are thoroughly protected by a series of U. S. and foreign patents. One of our fundamental claims covers the use of endless chains in tangential contact with numeral wheels, etc., broadly, which practically reserves for us the entire field of a durable and reliable computing machine of small dimensions and large capacity. The use of reacting keys necessitates a large key-board, with the accompanying noise and strain; the employment of rebounding bars is objectionable on account of the inaccuracies caused by the jar and friction and the wearing out of the controlling springs, etc.; resetting pins and cranks are too clumsy devices to be employed in performing the computations of the counting-room; returning tapes are too weak and elastic to form the basis of a mechanism the essential features of which are accuracy - 58 - and durability, and revolving disks are too awkward in manipulation and limited in capacity to, be even thought of in connection with a practical computing machine. The utilization of endless chains in combination with the development of other important features, solves the problem which we have set before ourselves, and places the computing machine, which has hitherto been a luxury of the favored few, within the reach of everybody who has use for it.
To those who are compelled to exercise their minds excessively, the Arithmachine brings rest and relaxation while those who strain the muscles of the hand and forearm by writing, making themselves subject to writer's cramp and nervous disorders, find relief in bringing into action different sets of muscles when manipulating the Arithmachine. The operation of writing, frequently performed under very unfavorable conditions, is also straining to the eyes, being creative in its nature and requiring close attention to direct and control the movement of the hand. The manipulation of the Arithmachine, as well as the reading of the results arrived at with its aid, is purely receptive, as far as the eyes are concerned, and therefore restful, the forms being plainly visible and all glare removed.

Size, 4½ x 1½ x ¾ in. Weight, less than 1 lb.
DESCRIPTIVE.
THE graceful and harmonious outlines of the Arithmachine are likely to impress themselves first upon the casual observer. The systematic arrangement and disposition of the operating elements will no doubt be noticed on closer examination, while the small size (4½ x 1½ x ¾ in.), light weight (less than 1 lb.), and smooth, noiseless action, as well as the convenient proportions of the machine, which permit it to be satisfactorily handled in many different ways and under varying conditions, are bound to please the operator and will be fully appreciated after a few moments' manipulation.
The operating surface, more distinctively called the chain-board, consists of the visible surface of a number of parallel and endless chains, the link of which present the appearance of straight and toothed bars, the joints on connections being invisible. The automatic alignment of the chain-links produces the impression of horizontal and equidistant lines across the chain-board, while the plain and milled, light and colored vertical partitions serve to complete the similarity to a blank book ruling, at the same time protecting the chain-links against disarrangement and breakage.
- 60 -The indicator opening at the head of, the Arithmachine is in the most, favorable position for reading the result, and the erasable tablet, in close proximity to it, proves a great convenience for making memoranda of examples and results. The eyes, glancing from the figure columns or given amounts to the chain-board and vice versa, remain in the same line of vision, a great advantage over the large and clumsy mechanisms previously introduced, and the front and rear ends of the machine are so formed and shaped as to furnish a convenient hold for the fingers, as well as a guide to the figures operated upon. The front end of the machine is also graduated to conform with the sectional division of the chain-board and blank book columns, and the hole at the rear end serves to fasten the Arithmachine to a hook on the desk, or to suspend it whenever it is desired to have both-hands free or to have it out of the way. It can also be fixed in position by means of a clamp or by resting it against a ledge or elevation at the edge of the desk or table, the operation of the machine causing a straight downward and forward pressure.
The double numeral and complemental scales are composed of two inside columns of large figures, which are intended to direct the placing of amounts in addition and multiplication, and two outside columns of small figures, which serve to guide the placing of amounts in subtraction and division. It will be observed that the large figures are repeated on both sides of the chain-board, which greatly facilitates
- 61 -
the placing of amounts in addition, the most important and frequent operation performed upon any computing machine. The scales of small figures are different on both sides, the left-hand scale being composed of complements of the adjoining large figures to nine, while the right hand scale of small figures is composed of complements of the adjoining large figures to ten. The number 10 at the bottom of the small right hand scale is indicated by placing the 1 inside of the large 0, which is intended to make the appearance of the scales symmetrical, and to point virtually to the large 1 in the tens column, which must be registered in place of it. The left hand scale of small figures is taken as guide in placing the figures of the subtrehend or divisor, excepting the units figures, which are placed according to the small figure of the right hand scale.
The sliding shutter, fixed in transverse, parallel grooves, serves to shut out from view any place or section in the indicator opening, or to separate it into two or more distinct divisions. It can be easily slipped out of the way by pushing it to the right or left, over either side of the case. The small head or catch on its convex surface serves to facilitate its manipulation, and a pin on the under side prevents it from falling off, or being lost.
A similar mechanical arrangement is employed in fastening the decimal point, which serves as a means at connecting the indicator above with the chain-board below, or to point off or separate any of the figures appearing in - 63 - the indicator opening. In its rest position it is generally kept as a means of separating the dollar from the cent columns.
The removable chain-covers are employed to cover up or to prevent the use of any chain or chains, which is very desirable in some computations. It can be easily placed in position, as its shape and material act like a spring, and the curved ends fit on the cylindrical rollers at both ends of the chain board sections. The surface of the chain cover contains the large numeral scale, which assists the eye in following the horizontal lines across the chainboard.
The movable stop, gliding forward and backward over the chain-board, can be readily slid out of the way at both ends, and its smooth and parallel movement is assured by the curved and turned compressing ends. It serves to facilitate the repeated placing of numbers in the same row and to limit the operating surface of the Arithmachine, which even in the full dimensions of the eight column machine covers only about 2½ square inches, and enables the operator to place thereon any number or amount between 1 and 999.999.99.
The resetting wheel, which has a milled or nurled periphery, serves to return the figures in the indicator opening to ciphers. It is held in position by a projecting pin on the underside, which is easily withdrawn by means of a lever spring and release button, and permits a complete revolution of the wheel.
The case, which is made of aluminum highly finished, is principally intended to protect the - 64 - operating mechanism, which is complete in itself. It also serves as a means of disposing and attaching some of the minor parts of the Arithmachine, such as the number scales, sliding shutter, decimal point, etc., on the upper and the small circular posts or rollers (which reduce friction when moving the machine over a blanks book column) on the under side.
The colors of the chain-board, number-scales, etc., are subdued, to prevent any unpleasant effect on the eyes, and to reduce the liability to mistakes.
The figures on the numeral wheels, visible through the indicator opening, as well as those on the U frame, in the numeral scales, are raised and polished, and the background is finished in a dark steel blue or oxydized copper, which produces a distinct and pleasing contrast.
NOTE.— With some slight modifications the Arithmachine can be easily transformed into a computing machine for the blind, the raised figures and its entire arrangement fitting it for this purpose. This would open up a channel of utility hitherto not thought of in connection with any computing machine.
Another unique feature of the Arithmachine is the arrangement of the name-plate at the front end of the chain-board, utilizing the M in the inventor's name also as the M in the word "Arithmachine," an illustration of economy, which the Machine is intended to give in other directions.
The pencil stylus, with which the machine is operated, consists of a triangular pencil and a triangular tip, which can be easily attached. The latter has a curved stylus-end, the curvature - 65 - being intended to bring the chain-links fully under the roller-lock at the forward end of the Arithmachine. It has the effect of strongly grasping the chain-links, enabling the operator to take a firm hold and to prevent slipping.
The form of the Arithmachine, particularly its profile, reminds one to some extent of the Sphinx, who, according to Greek mythology, proposed a riddle to every Theban who passed her, killing all who were unable to guess it. The riddle, according to tradition, inquired what being has successively four, two and three feet and is weakest when it has most feet. Oedipus answered: man, who creeps in childhood, afterwards goes erect, and walks with a staff, a third foot, when old. The Sphinx, in compliance with her own conditions, thereupon threw herself from the rock and died. Here, naturally, the comparison ceases. The Arithmachine, a modern sphinx, does not ask any arithmetical questions, but answers those put to it quickly and accurately, and as far as the temptations to commit suicide are concerned, they must remain greatest with those who decline to accept its beneficial ministrations.
DIRECTIVE.
THOUGH it is a great deal better to do right instead of wrong, and, as a rule, more convenient and profitable, the tendency of man since Eve's fruitful opportunity has always been towards transgressions. Therefore, directions are also necessary in regard to the treatment and operation of the Arithmachine, and while their non-observance will neither cause an explosion, as would be the case with a steam engine, nor an electrocution, which might easily happen with a dynamo, careful consideration of the advice and suggestions contained in the following paragraphs, will have the effect to reduce the wear and tear of the Arithmachine to a possible minimum, to increase its utility and durability and to insure its smooth and uniform action.
As above indicated the directions herein offered are naturally and necessarily of two kinds, those which refer to the "treatment" and those which pertain to the "operation" of the Arithmachine.
Treatment.
A complex mechanism, like the Arithmachine, possesses an almost human individuality. It will not do to handle it according to one's own notions, if it is desired to secure the - 67 - best results and greatest efficiency. One must try to enter into the spirit of the mechanism, as it were, to get closely in touch with it, to become familiar with its "peculiarities," and it will perform its work without unnecessary wear and to one's entire satisfaction. A machine of this kind bears the same relation to its owner as the slave of bygone days. It pays to take good care of it. One may drive and hound a free man, and let him go when he becomes worn out or inefficient, but the machine is your own property, and if ruined through carelessness it is your own loss.
Before leaving our factory the Arithmachine is thoroughly tested and all the bearings properly examined and "lubricated." A few drops of the finest watch oil are employed for this purpose, and after this has been done the machine may be allowed to remain "dry," and no further attention need be paid to this point. The adjustments are so accurate that a few weeks operation cause them to become as smooth as a mirror, and the addition of any oil or lubricant would only have the effect of interfering with the proper running of the mechanism.
Considering the value of the Arithmachine and its practical utility, it is almost superfluous to state that it is at least desirable to keep it free from dust and other harmful influences, such as extreme heat or cold, etc., and to insure it against the ravages of fire, water. cyclones, etc.
When carrying it in the pocket it should be properly protected by means of the Leather - 68 - Pocket Carrying Case or any other suitable enclosure, and its outside finish may be preserved by wiping it occasionally with at dry, soft cloth or chamois skin.
While accidental dropping of the Arithmachine will not necessarily interfere with the workings of the operating mechanism it is respectfully suggested that sudden jars or knocks of any kind are not likely to improve its outside appearance or strengthen the numerous parts, which make up the interior construction. The case is made in a very substantial manner and is intended to protect the operating mechanism against breakage, while giving the machine at the same time a very attractive and graceful appearance.
As there are, no doubt, a great many grown persons who have inherited from their little ones the desire to know the "inside of everything," the injunction not to open the Arithmachine, unless one is thoroughly familiar with the construction of complex scientific instruments, must not be deemed out of place. It is practically impossible for any one not versed in every mechanical detail of the Arithmachine. to properly put it together after it has been taken apart, and those who cannot control their curiosity, are either referred to the "mechanical" part of this book, or, will be furnished with a sectional diagram of the interior construction of the Arithmachine, which can be fully investigated without causing any damage to the latter.
Last, not least, it should be remembered that the demand for the Arithmachine is so great
- 69 -
About Actual Size.
and the supply yet so limited, that those who wish to remain in its possession should carefully guard it against any undue desire of unauthorized persons to become too familiar with its advantages. Our guarantee does not cover this point, while a lock and chain may accomplish the desired end.
Operation.
In approaching the Arithmachine with a view to operating it, it should be taken for granted that it objects to being abused by those unacquainted with its workings.
Those who at all aspire to the distinction of becoming successful arithmachinists must not fail to observe the following directions:
The operating surface or chain-board is locked when not in use, and it requires a special curved stylus, which is furnished with each Arithmachine, to set any of the chain sections in motion. Lead pencils, tooth picks, coffin nails, hair pins, etc., while splendidly adapted for the purposes for which they were originally devised, were never intended, nor can they safely or conveniently be employed, for properly manipulating the Arithmachine.
But even with the proper stylus some knowledge and judgment is required to use it satisfactorily. When operating the Arithmachine the stylus-pencil should be held in a nearly vertical position, as shown in the accompanymg illustration, which prevents friction with the adjoining partitions, permits the proper and easy insertion of the stylus point in the desired chain section and subdivision, and enables the
- 71 -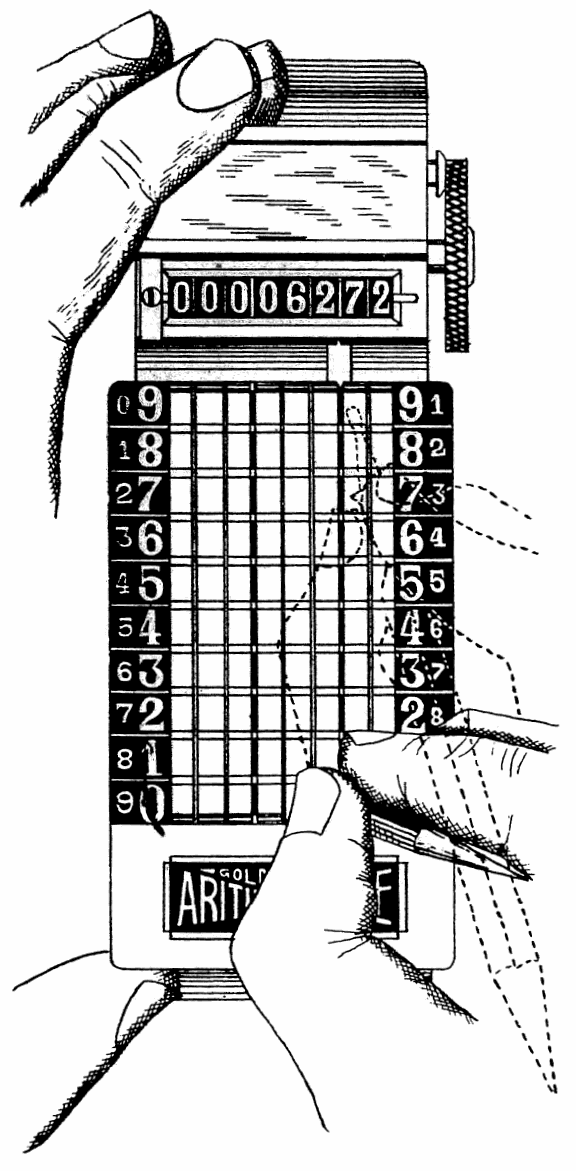
Nearly Actual Size - Eight Column Arithmachine.
operator to most conveniently and naturally exert the necessary pressure on the chain surface and underlying lever, to open the roller lock at both ends of the operating surface, and to insure the smooth and free movement of the corresponding chain. The curved stylus really represents a key to the Arithmachine, and, if retained by the operator, little fear need be entertained that any unauthorized person will interfere with the result, exhibited in the indicator, a great advantage over all other calculating machines, in which the slightest touch of the operating mechanism causes a derangement of the mechanism.
The "touch of the Arithmachine" is not hard but elastic, which greatly contributes towards ease and comfort in operating it, and the depression of the chain section, which automatically opens the chain lock, becomes after a little practice an unconscious act of the mind, like dipping the pen into the ink-well when writing rapidly. The habit should be acquired as early as possible to first depress and then pull the chain link, which not only results in the easy running of the chain, but also materially reduces the wear and tear of the machine.
The required depression of the chains is about onesixteenth of an inch, which is barely noticeable in rapid manipulation. The foundation of the chain-board being very substantial, no fear need be entertained of breaking any part by depressing fully; the danger lies rather in forcing the chain through the chain-lock without proper depression.
The pressure of the stylus pencil on the operating surface should be uniform, and the - 73 - stroke can be executed as slowly or rapidly as may desired by the operator or be required by the occasion. The moment necessary to insert the stylus-point and depress the chainlink can be profitably employed to make sure that the proper subdivision of the "chain-board has been selected, and in case of an oversight one has time to change the-position-of the stylus, before any harm has been done. The stylus should be held firmly and with the curved point toward the operator, which is accomplished without difficulty, the triangular Arithmachine stylus-pencil being an aid in this direction. When the roller-lock at the forward end of the chain board is reached, the curvature of the stylus surrounds the cylindrical roller and brings the tooth of the respective chain-link sufficiently under the roller, to lock it in position when the stylus is removed and the pressure of the platform lever spring asserts itself.
The stylus-point should always be held slightly above the chain board, not to waste any time in trying to reach it, and the curved end of the stylus does not hinder its gliding back over the chain links, which may become desirable when the registration of the same figure is to be repeated a certain number of times.
In order to reset the indicator to zero, the release button should be depressed with the middle finger, then the nurled resetting wheel is given about two semicircular turns in the opposite-direction of the movement of the chains. The release button need only be pressed for a - 74 - moment in order to unlock the wheel, and the latter may be turned by the thumb and the middle finger one complete revolution, if preferred. In the latest construction of the Arithmachine the resetting wheel must not be returned to its original position, after the numeral wheels have been set to zero, but is, in
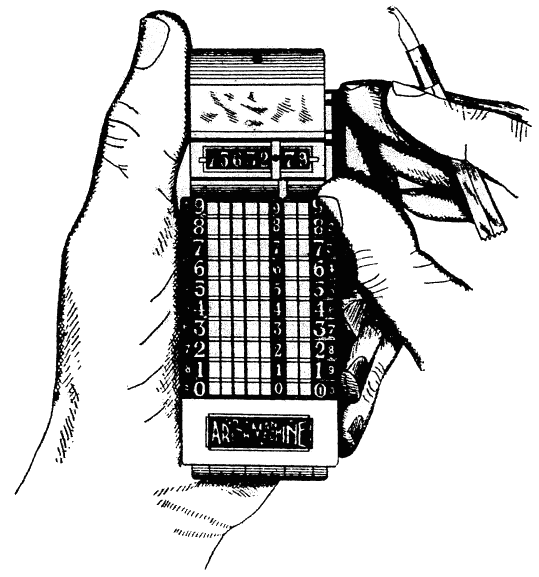
About Half Size.
place for the operation of the mechanism, while in the earlier arrangement it is essential to return the resetting wheel until the release pin engages the hole, which may be noticed by a snapping sound. Otherwise the machine is likely to carry incorrectly, and besides is subject to considerable wear and strain.
- 75 -When resetting the indicator to zero, it is quite interesting to note the manner in which the faces of the numeral wheels are changed. By turning the resetting wheel slowly from the operator the figures are picked up and carried along in numerical order, irrespective of the position in which they are found, which will give a due appreciation of the mechanical construction of the Arithmachine. The ones disappear first, then the twos, threes, fours, etc., until finally all the zeros are reached.
The Arithmachine can be easily moved over a blank book column, acting as guide to the figures operated on, and being held in position
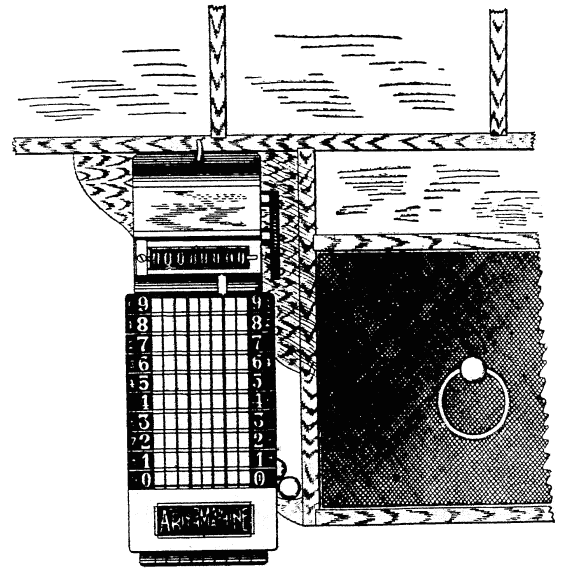
About Half Size.
by the thumb and middle and digit fingers of the left hand, as shown in the illustration on page 85. It can be firmly, held in the - 76 - left-hand by surrounding it with the thumb on one side and the remaining four fingers on the other. It can be fastened to the desk by a hook which is inserted into the hole at the head of the machine or a clamp which holds the head and foot. It can be suspended by a hook, used as a paper weight, carried in the vest pocket; in short, it quickly conforms to any conditions which are likely to arise while serving the purpose for which it is intended.
About Half Size.
In regard to the attachments and accessories, which accompany the Arithmachine, a few remarks will be found of practical assistance in their manipulation.
The chain cover can be readily attached to any section by pressing the farther end against - 77 - the small cylindrical roller, and allowing the forward end to snap in position.
The sliding stop can be moved out of the way at both ends of the chain-board, and being rarely used may be entirely detached from the machine and kept in reserve.
The decimal point slides easily to the left or right, but is generally kept between the dollars and cents columns, pointing upwards, to the indicator and downwards to the chainboard. It can only be detached by using force, which is very appropriate in war, but not required in handling the Arithmachine.
The digit shutter is generally placed over the left-hand side of the case, and may be easily moved in position to cover or hide any of the figures or figure spaces in the indicator. It can also be moved out of the way to the right, and slipped over the side of the case close to the resetting wheel.
The erasable tablet serves to record an example or result, or any of the facts or figures required in performing a more complex computation, which cannot be easily retained by the memory.
The graduation marks at the front end of the machine are intended to conform with the unit lines of a blank book column, and a similar effect is produced by the distinguishing features of the separating partitions of the chain-board and indicator opening.
The stylus-point is easily fastened to or detached from the triangular stylus-pencil, and remains a permanent fixture, which, with ordinary care is likely to outlast the Arithmachine, - 78 - while the triangular stylus-pencil can be used up and replaced.
The Pocket Carrying Case serves to preserve the finish of the aluminum, case and to prevent any particles from clogging up the operating mechanism.
Directions which more specifically refer to the utilization of the Arithmachine as a calculating instrument, particularly the instructions necessary to perform with it the different arithmetical operations, are properly reserved for the following subdivision of this work.
A remarkable demonstration of the convenience and practicability of the Arithmachine consists in hiding it from view by the palm of the hand. To be able to accomplish this with a mechanism, performing all arithmetical operations, and carrying eight or more columns simultaneously, represents not only a mechanical achievement of considerable importance, but is bound to prove an interesting feature of commercial value, by exciting the curiosity and attracting the attention of many, who could otherwise not be induced to investigate its manifold advantages; The "Arithmachine grip" is likely to introduce the science of Mechanical Arithmetic to those contented souls, who have succeeded in fortifying themselves against modern influences with that Chinese wall, commonly called indifference.
INSTRUCTIVE.
WE enter now upon the most important subdivision of this work, which, while primarily intended to serve as a practical self-instructor in the proper manipulation and utilization of the Arithmachine, contains many valuable points of information, which have a direct bearing on Mechanical Arithmetic in general, and will be found useful in connection with other computing devices of similar capacity.
The knowledge of Mechanical Notation, of the use of the double complemental scales, the methods of performing the four species of arithmetic, as well as involution and evolution and complex computations by mechanical means, is likely to become an indispensable feature of modern education, and invaluable as a practical accomplishment.
Mathematics, the oldest and most firmly established of all sciences, welcomes its latest offspring, Mechanical Arithmetic, as yet unknown to the vast majority who are likely to be benefited by its services, and hardly recognized by those who lay claim to a broader scientific training. But a few years are likely to change this condition of things, and anyone not familiar with the principles of mechanical computation may be pronounced a "back-number," if not an ignoramus.
- 80 -Mechanical Notation.
A superficial examination of the Arithmachine will disclose a rectangular surface, called the chain-board, lined on either side by a double scale of numbers, and divided into a series of narrow sections by means of distinguishable partitions. Back of the chain-board and in a slightly elevated position is the indicator opening in the case, which for the sake of brevity, we will call the indicator. The same partitions which subdivide the chain-board into a series of columns subdivide the indicator into a number of places.
The relation of these columns and places conforms with the decimal notation, the first section to the right denoting units, the second tens, the third hundreds, the fourth thousands, or in case the first two columns are reserved for cents, the remaining columns stand for dollars. Thus it will be, noticed that the arrangement of the Arithmachine is perfectly natural, and there ought to be not the least difficulty of familiarizing one's self with it.
To place a number on the Arithmachine, the large figures on both sides, constituting the fundamental numeral scales, are taken as guides, and the stylus-point is inserted in the proper place in the desired column of the chain-board and moved forward to the chain-stop, as described in the preceding chapter. To indicate 3, for instance, the stylus-point is inserted in the place opposite the large 3 in the numeral scale in the first right-hand, chain-column and moved forward to the chain-stop; to indicate to the stylus-point is inserted opposite the large 7 in the second column and moved forward to the - 81 - stop, etc. In either case it will be observed that the figure registered actually appears in the proper place in the indicator, provided the latter had previously been set to zero.
A number composed of two or more significant figures is placed on the Arithmachine, by indicating the several figures successively, as above described, and it is practically immaterial whether the figures are placed from the left to the right or from the right to the left, as far as the mechanical operation of the machine is concerned, though it is most convenient to register numbers and amounts as they are pronounced, viz., from the left to the right. Ciphers, in whatever position they may be found, are not registered on the Arithmachine, the place value of the significant figures being clearly defined by their position in the indicator and the columnar arrangement of the chain-board.
The decimal relation of the chain sections or columns may be interrupted or ignored by employing the chain cover and wheel shutter, to cover up or remove from view any of the chain sections. This original feature of the Arithmachine is of particular value in operating with common fractions, denominate quantities, etc., and will be more fully explained under these heads.
Double Complemental Scales.
We have so far only referred to the placing of a number according to the large figures, composing the fundamental numeral scales, on both sides of the chain board. This operation will be briefly described as placing a number "large." But there are two other numeral scales in the - 82 - outside columns of the frame plate, smaller in size and different in arrangement, the purpose of which has not yet been explained.
A careful inspection, will disclose the fact that the small figures on the right-hand side of the chain board are the complements of the adjoining large figures to 10, while the small figures on the left-hand side form complements to 9 with the adjoining large figures. These scales, characterized by smaller figures, are termed Complemental Scales, and their invention and utilization is entirely new and original with the author.
The regular definition of an arithmetical complement is the difference which a number lacks to 10 or the next higher power of 10, but we employ in the Arithmachine, for practical reasons to be explained, two complemental scales, the one composed of complements to 10, and the other of complements to 9.
To place a number "small" or "complementally" on the Arithmachine, the small figures on the left-hand side of the chain-board are taken as guidance, excepting for the units figure of the amount or item to be registered, which is placed according to the small figures on the right-hand side. The effect of this operation is clearly shown in the following example:
| By placing | 567 | "small," we actually register | |
|---|---|---|---|
| 433 | according to the large numeral | ||
| ---- | scale, the sum of which is | ||
| 1000. |
The terms "positive" and "negative" for the fundamemtal and complemental numeral scales are misleading, and have been carefully avoided in this connection. Other calculating machines, having only a single complemental scale, overcome this deficiency by the instruction to register "1 less" for the units figure, which is a mental process liable to be ignored and to cause inaccucies.
Nines in numbers which are to be placed "small" or "complementally" are not registered, excepting when they appear in the units places. The small 0 in the right-hand complemental scale points to the small 1 in the large 0 of the right-hand fundamental scale, and requires the registration of 10 according to the large figures. In other words, a cipher in the units place of any number is registered "small" by placing 10 "large" on the Arithmachine, the reason for this being self-evident, when the relation of the fundamental and complemental scales is once understood. With the aid of the fundamental and complemental numeral scales all operations of arithmetic may be reduced to addition, which, while not always practicable, contributes to a better understanding of these processes.
Machine Addition.
To add a "column of figures" or rather a "page of items" on the Arithmachine, the amounts are placed successively according to - 84 - the large numeral scales. The best method consists in starting at the head of the page, resting the machine on the book or sheet, and keeping, the figures to be operated on at the front end of the machine; then moving the machine forward and downward, always following up the amounts, and employing the machine as guide to the figures. If interrupted in the middle of a page or column, the indicatoin exhibits the total of the figures added, while the forward end of the Arithmachine points to the next item to be registered. When the bottom of the page is reached the machine can remain in its last position until the total has been copied from the indicator.
An indirect benefit resulting from the adoption of the Arithmachine is the ability to at all times pay immediate "attention to outsiders, without sacrificing any part of the work done, which is bound to obviate dissatisfaction in front of the bookkeepers desk and a considerable amount of swearing behind it.
In following this course the items to be added are always kept between the Arithmachine and the operator, while the result appears at the farther end of the machine, which is the best disposition, in order to avoid mistakes and to attain speed. With the larger computing machines, requiring separate desk space, these important points are necessarily sacrificed.
The advantage of being able to keep the eyes continually on the work while operating the Arithmachine, or the convenience of following the figures of the given column with the machine itself, must be experienced in order to be thoroughly appreciated.
- 85 -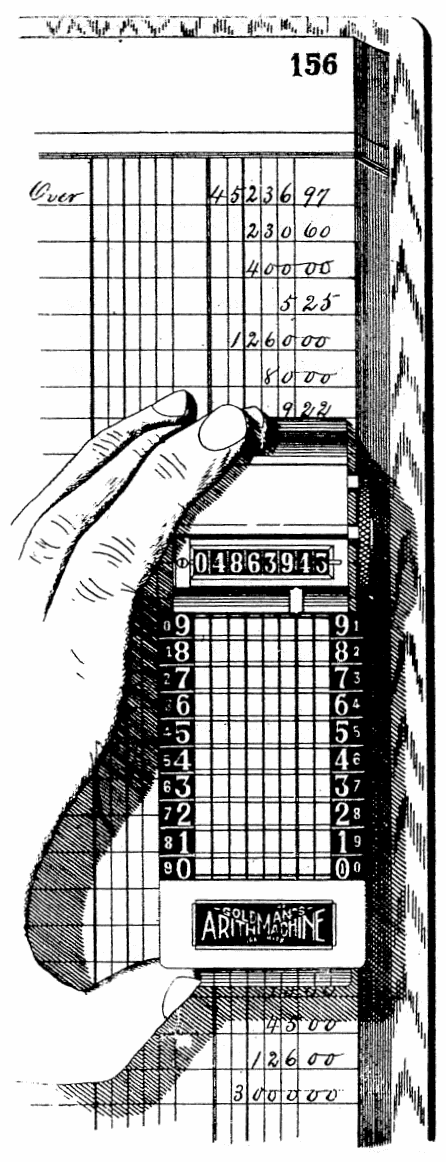
About Half Size.
| ILLUSTRATION. | ||
| 423.56 | Partial Results. | |
|---|---|---|
| 12.98 | 423.56 | |
| 5645.27 | 436.54 | |
| 36.18 | 6081.81 | |
| 5.19 | 6117.99 | |
| 617.23 | 6123.18 | |
| 589.40 | 6740.41 | |
| 763.25 | 7329.87 | |
| 200.00 | 8093.12 | |
| 50.00 | 8293.12 | |
| ------- | ------- | |
| 8343.12 | 8343.12 | |
Explanation.— By placing the amounts on the lefthand side of the above illustration in their regular order in the Arithmachine, the partial results exhibited on the right-hand side appear successively in the indicator. It is evident that columns of any desired length can be added by this process without increasing the difficulty or in any way complicating the operation.
The operation of machine addition can also be performed by commencing with the items at the bottom of the page and proceeding towards the top, in which case the head of the machine serves as guide, and the Arithmachine is particularly adapted for adding separate or scattered items without listing them, and for footing amounts, which appear side by side instead of under each other, so-called "horizontal addition," as is often required in retail ledgers, summaries, recapitulation sheets, etc.
| ILLUSTRATION. | ||||||
| 423.61, | 129.82, | 647.23, | 845.26, | 329.64 | │ | 2,375.56 |
|---|---|---|---|---|---|---|
| 523.82, | 156.24, | 685.43, | 143.26, | 729.63 | │ | 2,238,38 |
| 457.86, | 247.89, | 729.56, | 527.62, | 51.42 | │ | 2,014.35 |
| 124.23, | 642.23, | 223.42, | 823.40, | 843.56 | │ | 2,656.84 |
| 627.49, | 529.84, | 716.25, | 621.52, | 122 57 | │ | 2,617.67 |
| ————————— | ——————————— | ——————————— | ——————————— | —————————— | —│ | —————————— |
| 2,157.01, | 1,706.02, | 3,001.89, | 2,961.06, | 2,076.82 | │ | ll,902.80 |
Explanation.— The amounts are added horizontally and extended in each line. They are then footed vertically and placed under the corresponding columns. The partial totals are then footed horizontally and vertically, which final results must agree. All these operations are conveniently performed with the Arithmachine, and the danger of considering a figure in the wrong place or column is entirely eliminated. The skipping over amounts, in order to place the figures in numerical order. according to their location on the chain-board, is not desirable.
A great step forward in mechanical addition is accomplished and considerable time saved
|
PLACING SEPA-
RATE ITEMS. About Half Size. |
by grouping amounts, viz.: assisting the machine by performing some of the simpler operations mentally and registering the intermediate - 88 - results, the machine acting virtually in the capacity of an automatic memory, which carries the partial totals from the top to the bottom of the page. The Arithmachine is thoroughly adapted for this class of work, as it can be conveniently employed to keep track of the items already considered, and because the items to be combined are readily seen in front of the machine, while those already added are covered by it. The grouping of amounts is thus easily accomplished and without the least danger of mistake or confusion.
| ILLUSTRATION. | |||||||
| Amounts Placed. | Partial Results. | ||||||
| 450.23 | |||||||
|---|---|---|---|---|---|---|---|
| 12.20 | 462.43 | ||||||
| 500.00 | 462.43 | ||||||
| 6.90 | |||||||
| 3.10 | 510.00 | ||||||
| 255.10 | 972.43 | ||||||
| 40.00 | |||||||
| 50.00 | |||||||
| 5.00 | |||||||
| 200.00 | 550.10 | ||||||
| ———————— | |||||||
| 1,522.53 | 1,522.53 | ||||||
Explanation.— The first column contains the given items, the second column exhibits the amounts placed in the machine, while the third column shows the partial results, which appear successively in the indicator. The braces mark the items which have been combined by mental operations.
When totals are to be carried forward from page to page the Arithmachine performs the operation automatically, as it retains the last footing in the indicator, and is immediately ready for proceeding with the following page. - 89 - If a new addition is to be commenced the indicator can be set to zero instantaneously.
Additions, exceeding the capacity of the Arithmachine, can still be performed with it, by prefixing 1 in front of the highest, and deducting 1 in the lowest place of the result, as shown in the indicator, for every time the full limit of the machine has been passed. For instance: If the indicator exhibits 042369.43, and the limit of the eight-column Arithmachine has been passed once, the correct total would be 1042369.42, which can also be obtained by the lengthy process of adding 999,999.99, which is 1,000,000.00 less 1, to the result found in the indicator. This rule, of course, refers only to such columns, in which there are no larger amounts than can be placed on the machine. If such items should occur, the figures exceeding the capacity of the Arithmachine must be left for a separate registration, to be performed after the main process has been completed.
An extreme test, sometimes applied to computing machines and numbering devices, is to carry the entire series of nines, by the addition of 1 in the lowest column. While the Arithmachine is perfectly equipped to accomplish this task, it ought not to be subjected to it in a playful spirit, for two reasons. In the first place there is hardly any practical requirement which necessitates it, and secondly, it subjects the carrying mechanism to useless wear and strain.
If desired by the operator additions can also be performed by single columns, as in ordinary mental footing, with or without mental combinations, but the great advantage of the Arithmachine - 90 - consists in enabling anyone to add any desired number of columns simultaneously, bringing within easy reach of ordinary calculators the enormous advantage possessed by lightning calculators, a comparatively limited number of specially gifted minds. The simultaneous addition of all columns also saves the careful going over lengthy columns, the picking out of scattered figures, the frequent mistakes of carrying wrong hundreds or resulting from crowding two figures into one place. Considering in addition to these unquestionable advantages, the feeling of mechanical accuracy in the place of the usual, mental uncertainty, the relief from nervous strain, the absolute ease, quiet and comfort with which the Arithmachine can be operated, and the ability of grasping the amounts and controlling the chain-board without a turn of the head or a move of the hand, who, excepting those in straitened financial or intellectual circumstances, would be willing to do without Goldman's Arithmachine, when its merits and benefits have become, fully known?
Machine Subtraction.
The process of subtraction is performed on the Arithmachine by registering the minuend according to the large or fundamental numeral scales, and placing the subtrahend according to the small or complemental numeral scales, eliminating the 1 in the highest place of the result, which appears in the indicator. In other words, in order to subtract we add to the - 91 - minuend the complement of the subtrahend, and deduct from the sum the next higher power of 10.
| ILLUSTRATION. | |||
| Minuend | 45692.37 | Minuend | 45692.37 |
|---|---|---|---|
| Subtrahend | 16458.79 | Complement | 83541.21 |
| ———————— | ————————— | ||
| Difference | 29233.58 | Total | 129233.58 |
Explanation.— The first illustration exhibits the ordinary method of subtraction, while the second shows the process as performed with the Arithmachine. By registering the subtrahend according to the complemental scales, the difference between the subtrahend and the next higher power of 10, in this instance 100000.00, is added to the minuend. The total, therefore, must be reduced by 100,000.00, in order to be equal to the difference of the given amounts.
The elimination of the 1 in the highest place of the result in the indicator can be accomplished by one of the following methods:
- It may be simply ignored by the operator, who fully understands its meaning.
- It may be removed from view by moving the wheel shutter over the place adjoining the highest figure in the minuend.
- It may be thrown out of the machine entirely by registering the minuend and subtrahend in the left-hand columns of the Arithmachine.
The method of removing a figure from the indicator as explained under the head, "Correction of Mistakes", being somewhat laborious, need not be resorted to in this connection.
In placing the subtrahend complementally, it should be remembered that it must have as - 92 - many places as are contained in the minuend, and whenever the subtrahend has a lesser, number, these vacant places are indicated by registering ciphers (nines) complementally.
| ILLUSTRATION. | ||
| 453.26 | 453.26 | |
|---|---|---|
| 19.81 | 980.19 | |
| —————— | —————— | |
| 433.45 | 433.45 | |
Explanation. The vacant place in the subtrahend is supposed to contain a 0, and the complemental 9 is registered instead. Nines in the subtrahend are entirely ignored, as they are equivalent to fundamental ciphers, excepting in the units place, where they call for the placing of the large 1. A 0 in the units place of the subtrahend is registered by placing the large 1 in the second column, the complement of 0 being 10.
A more complex method of subtraction consists in registering the minuend "small" and the subtrahend "large," in which case the difference, appearing in the indicator, must also be read complementally.
| ILLUSTRATION. | ||
| 8643.29 | 1356.71 | |
|---|---|---|
| 2874.57 | 2874.57 | |
| ——————— | ——————— | |
| 5768.72 | 4231.28 | |
| Complemental difference, | 5768.72. | |
Explanation.— The only advantage of this plan is the elimination of the 1 in the highest place of the result by means of doubling the complemental process; but it is an advantage too dearly bought, unless the numeral wheels, could also present the complements on their faces, which again would be rather confusing in some instances. A method of complemental addition is also possible, but entirely impracticable.
Subtractions of numbers, exceeding the capacity - 93 - of the Arithmachine, can be performed with its aid by separating the given items into two sections and registering the units figure of the left hand section of the subtrahend according to the left hand complemental scale, in case the adjoining figure in the right hand section of the subtrahend is larger than the corresponding figure of the minuend. Otherwise the two sections are treated like two separate subtractions and the differences joined afterwards.
Machine Multiplication.
The process of multiplying is best performed on the Arithmachine by simply registering the partial products of the multiplicand by the figures of the multiplier, taking care that the results of these operations are placed into the proper columns. The machine does all the carrying and adding, requiring the operator to do no more than to register successively-the products of the multiplication table. The placing of these products can be proceeded with from the right to the left or vice versa, at the option of the operator, the machine carrying the tens correctly either way.
| ILLUSTRATION. | ||
| 1. To multiply | 44 | by |
|---|---|---|
| 21 | register successively | |
| ——— | ||
| 44 | then move one place to | |
| the left and register, | 88 | when the product |
| ———— | ||
| 924 | will appear in the indicator. | |
| 2. To multiply: | 457 | by |
|---|---|---|
| 324 | register successively | |
| --- | ||
| 28 | ||
| 20 | ||
| 16 | then move one column to | |
| the left and place | 14 | |
| 10 | ||
| 8 | then move again one place | |
| to the left and indicate, | 21 | |
| 15 | ||
| 12 | when the product | |
| ------ | ||
| 148068 | will be seen in the indicator. |
Explanation.— The mind reports the products of the multiplication table mechanically and the machine does the rest. The advantage of this method over the old way must be experienced in order to be fully appreciated, and certainly no distinct illustration in print can do it justice, as all processes are performed on the Arithmachine on a single line in the indicator.
A still shorter method consists in carrying mentally the tens of the partial products, which saves placing a number of figures on the machine.
| ILLUSTRATION. | |
| 461.23 | Successive results |
|---|---|
| 21.45 | as they appear |
| —————— | in the indicator. |
| 23 0615 | |
| 184 492 | 23.0615 |
| 461 23 | 207.5535 |
| 9224 6 | 668.7835 |
| ————————— | ————————— |
| 9893.3835 | 9893.3835 |
Explanation.— Only the figures shown in the above illustration are actually placed on the machine. The tens are always carried mentally. The decimal point is moved to the fourth place, four being the sum of the - 95 - number of decimals in multiplicand and multiplier. The results of all operations appear successively in the indicator. Care must be taken that the figures are placed in the proper columns, which can best be done by holding the stylus-point in the position of the operator just completed, until the operator is ready to proceed with placing the next figure.
A method of machine multiplication, advocated in connection with a large computing machine, consists in placing the multiplier and the figures of the multiplicand as often on the machine as the figures of the multiplier indicate, or vice versa. This operation is somewhat simplified by placing each figure in the multiplicand as often as the figures of the multiplier successively indicate, which permits remaining in the same row of figures for a time, by simply changing the column.
| Explanation.— To multiply 87 by 65, place successively 7 five times in the first col- umn and six times in the second column; then move one place to the left, and place 8 five times in the sec- ond and six times in the third column, when the an- swer 5655 will appear in the indicator. A small example has been charitably taken to illustrate this awkward method. The same problem can be solved by the first method with seven move- ments, and by the second with six, while it requires not less than twenty-two strokes to follow out this plan. |
In multiplication particularly the province - 96 - of a computing machine is to perform those operations, which are laborious and tedious to the mind, particularly the carrying of figures and the addition of the partial products. These processes the Arithmachine performs automatically and simultaneously, as soon as the partial product of any two figures is placed. And it is a great deal safer, better and easier to register four separate partial products of two figures each, than to place two different figures in different columns, together twenty-two times; twenty-two distinct impulses of the mind carried out by the hand, not to speak of the bad effects on eyes and ears, caused by these continuous and rapid vibrations and the deafening rattle of numberless keys. Of course to the few desiring to become brainless idiots with strong fists a similar course is open on the Arithmachine, while all who wish to retain their mental faculties unimpaired, or rather develop them by congenial and restful exercise, will never heed such folderol. It is partly due to the advocacy of such awkward and unnatural methods that Mechanical Arithmetic has not yet taken the place it deserves in the school room and the business office.
To multiply large numbers, the product of which-exceeds the capacity of the machine, the process of "sectional" multiplication is recommended. It consists in separating the multiplicand or multiplier in two or more sections, to perform the sectional multiplications on the machine and to combine the partial results. In deciding how best to do this it will be helpful to remember that the product of a multiplication - 97 - generally requires as many places as the sum of the number of places in multiplicand and multiplier indicates. To illustrate: A multiplicand Of six places and a multiplier of four places, will as a rule, result in a product of ten places, therefore if an eight column machine is at one's command, it would be desirable to separate the multiplier into two sections of two figures each, the sectional results of which are both within the eight column capacity of the machine.
Note.— The sectional separation of multiplicand and multiplier is not desirable, as it divides the computation unnecessarily in too many disconnected processes.
| ILLUSTRATION. | ||||
| 684329 | 684329 | 684329 | ||
|---|---|---|---|---|
| 2761 | 61 | 27 | ||
| ---------- | ---------- | ---------- | ||
| 41744069 | 684329 | 4790303 | ||
| 18476883 | 4105974 | 1368658 | ||
| ---------- | ---------- | ---------- | ||
| 1889432369 | 41744069 | 18476883 | ||
Explanation.— The multiplier 2761 is separated in two sections, 27 and 61. The separate multiplications are then performed on the machine, and the results recorded on the erasable tablet or on a separate sheet, placing the second result two places to the left, but under the first. The addition can then be performed on the machine, while the two highest figures, for which there is no room, are simply copied.
Space does not permit to present here the numerous contractions, contained in various books on arithmetic, all more or less applicable or adaptable to machine computation. Those who are inclined to develop their ability in this direction will find a large number of valuable short cuts and "lightning methods" in Goldman's Expert Calculator, which offers also many new - 98 - ideas and suggestions with reference to the manipulation of numbers, not presented in any other work published.
Machine Division.
To divide with the Arithmachine, place the dividend in the indicator, according to the large number scale, reserving one place to the left for the first quotient figure. Then see how often the divisor is contained in the first partial dividend, and register the former according to the complemental scales, in the columns occupied by the latter, as often as it is contained therein. The first quotient figure will appear in the vacant place of the indicator, and the place or places first occupied by the partial dividend will exhibit the figures of the first remainder. A figure of the dividend is then annexed, and the operation repeated until every figure of the dividend has been employed. Additional decimals can be computed by annexing as many ciphers as the capacity of the machine will permit. To shorten the process materially, the products of the divisor by the quotient figures can be registered at once, according to the instructions given for multiplication, which saves the repeated registration of the figures of the divisor. The quotient figures appear successively to the left of the partial divisors, indicating virtually the number of complements to the next higher power of ten, which have been added by the operation. And so it happens that what in mechanical subtraction has been found a slightly awkward feature, proves in mechanical division of considerable value.
- 99 -
| Explanation.— 1. The black-faced figures are the figures of the quotient, which appear successively in the place of the dividend, until at last the dividend has been entirely removed and quotient and remainder are shown in the indicator. The movable wheel shutter may be advantageously employed to follow up the operation and to point off the partial dividend next to be considered. | ||||||||||||||||||||||||||||||||||
| 2. The products of the arithmetical complements of the divisor by the quotient figures are registered according to the fundamental numeral scales, and if complete, this can be done from the right to the left, in the order that the partial products are arrived at. Whenever the partial remainder is larger than the divisor or the quotient figure is smaller than the number of the multiple registered, it is a sign that the quotient figure is incorrect. In this manner the method of complemental division calls attention to any mistakes made. | ||||||||||||||||||||||||||||||||||
| 3. In this example two additional places of the quotient have been ascertained by means of annexing ciphers, which on the machine is done automatically, the ciphers appearing in the indicator to the right of the dividend. The decimal point can be, utilized to mark the decimal places of the quotient. | ||||||||||||||||||||||||||||||||||
NOTE.— The units figure of the divisor must always be registered according to the right-hand complemental scale.
A little practice ought to enable anyone to perform division on the Arithmachine without material difficulty, the processes being comparatively simple, and, to the beginner at least, exceptionally instructive and fascinating. If the short method of division here explained proves at first too difficult, the repeated registration of the divisor can be employed for a time, until thorough mastery over the process is attained.
Whenever the dividend exceeds the capacity of the Arithmachine, it can be parted into two distinct sections, and the two divisions performed separately. The remainder of the left hand section is then prefixed to the right hand section and the operation continued, while the result of the first division is placed on the erasable tablet, to be combined with the quotient of the second division.
A large variety of short cuts may be employed in connection with the Arithmachine, and some of the most valuable ones will be found in Goldman's Expert Calculator, referred to in the preceding chapter. Division can also be transformed into multiplication with the aid of reciprocals, and extensive tables have been prepared for this purpose. The best of these are Barlow's tables, containing the reciprocal values of numbers from 1 to 10,000, besides tables of squares and square roots, cube and cube roots, etc.
NOTE.— The black-faced type denotes the quotient figures, which successively appear in the indicator.
- 101 -Combined Operations.
The fundamental processes of computation, as explained in the preceding chapters, are frequently combined in actual work, and a few practical suggestions will prove of value in this connection.
The operations of addition and subtraction occur most often in balancing accounts. The Arithmachine accomplishes this task by a single and continuous operation, by registering the amounts of the larger side of the account according to the large figures, and the amounts of the smaller side of the account according to the small figures on the numeral scales. The difference or balance of the account appears in the indicator, without having first obtained the totals of the two sides.
| ILLUSTRATION. | ||||||||
| Dr. 43.56 | Cr. | 6 | 1 | . | 2 | 3 | ||
|---|---|---|---|---|---|---|---|---|
| 3 | 8 | 7 | 7 | |||||
| 21.47 | 3 | 5 | . | 4 | 6 | |||
| 6 | 4 | 5 | 4 | |||||
| 89.61 | 2 | 7 | . | 3 | 2 | |||
| 7 | 2 | 6 | 8 | |||||
| 57.42 | 3 | 8 | 8 | . | 0 | 5 | ||
Explanation.— The balance 388.05 is practically arrived at on the Arithmachine without any knowledge of the total on either side of the account. The small 3, which also appears in the register, indicates the number of items which have been placed according to the complemental scales and must be disregarded.
This method is particularly valuable in bank ledgers, as it greatly facilitates the daily extending of the undivided balances.
Addition and multiplication are generally combined in the work of bill clerks, etc., which requires the making of extensions and footings. - 102 - The products registered on the Arithmachine are simultaneously added and the totals can be seen at any time.
Addition and division occur most frequently in averaging accounts, etc., and the total of the items registered can be allowed to remain in the indicator, as it represents at the same time the dividend of the succeeding division.
The Arithmachine readily demonstrates its superiority over mental and manual computation in problems of interpolation, which consist in dividing the difference of two given amounts by a certain number, and adding or deducting the quotient successively to or from the smaller or larger amount, until the other is reached.
Subtraction and multiplication and subtraction and division are not required as often as any of the preceding combinations, though they can also be performed with ease on the Arithmachine, and as a rule permit the result of one operation to remain in the indicator, and to be employed in connection with the other.
Perhaps the most common of all combined processes is multiplication and division. It occurs in the solution of proportions and equations, in the reduction of denominate quantities, and in a hundred and one computations too numerous to mention. In nearly all instances it pays to divide first and to multiply afterwards. By so doing the calculation is materially decreased, and while this suggestion may appear superfluous to many, it is a fact, nevertheless, that it is seldom heeded.
- 103 -Common Fractions.
In computing with common fractions it is best to reserve the right-hand columns of the Arithmachine for the purpose, and to make the separation complete the chain-cover is inserted over the third column.
To add common fractions of the same denominator the numerators are registered in the right-hand columns, according to the large numeral scales, and the sum reduced by registering the next lower multiple of the denominator, according to the small numeral scales, and placing the number of the multiple in the columns to the left of those reserved for fractions, representing integral or whole numbers. In case the fractions are not of a common denominator, they should first be transformed, by employing the process applied in such cases in mental or written arithmetic, utilizing the Arithmachine to register the partial results. The movable wheel shutter can be used to exhibit the same separation in the indicator, which has been effected on the operating surface with the aid of the chain-cover.
When adding common fractions, which have a common denominator larger than 10, it is desirable to set aside the three right-hand columns of the Arithmachine, to accomodate the placing of the required multiple of the denominator on the chain-board, in order to extract from the sum the number of wholes contained therein.
This process is illustrated on the succeeding page.
- 104 -
| Explanation.— The chain-cover is placed over the 3rd column, and the number of eighths corresponding to each fraction are registered in the first right-hand column. Over the total 37 register complementally the next lower multiple of 8, which is 32, and the 4, representing the number of the multiple, is carried in the column to the left of the chain-cover. The whole numbers can be registered simultaneously with the numerators, so that the final total is reached in the whole and fractional columns at the same time. The 1 appearing in the indicator between the spaces reserved for whole and fractional numbers is removed from view by the wheel-shutter, which completes the separation of the Arithmachine into independent subdivisions. |
The above example simply serves to illustrate the method of utilizing the Arithmachine in operating with common fractions, which can be modified to fit special requirements and conditions.
Subtraction is performed by registering the numerator of the common fraction in the minuend, according to the large numeral scale, and the numerator of the fraction in the subtrahend, according to the small numeral scale. Whenever the numerator in the fraction of the minuend is smaller, increase it by one, expressed by the denominator, before subtracting.
| Explanation.— The one which is carried is made allowance for by registering the units figure of the subtrahend according to the left-hand complemental scale. The 1 which appears in the highest place of the difference is ignored, as is usual in subtraction of whole numbers. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Multiplications with common fractions resolve themselves into the corresponding operations of whole numbers, according to wellknown principles. But the method of multiplying, by making use of aliquot parts, which is favored by many on account of its brevity, is perfectly adapted to machine computation, as will be seen in the following illustration, especially if only a limited number of decimals is required:
| Explanation.— The partial products of the multiplicand by the whole number of the multiplier are registered first, then the parts of the multiplicand, which constitute the % of the multiplier, are successively registered, producing an approximately correct result, which is exhibited in the indicator opening. | |||||||||||||||||||||||||||||||||
Division can be resolved into multiplication by inverted divisor, therefore no special instructions need be given in this connection.
In employing the Arithmachine common fractions can often be readily reduced to decimals and the computation performed as with whole numbers.
Denominate Quantities.
The machine methods of computation with denominate quantities somewhat resemble those employed with common fractions, the chain-cover being utilized in a similar capacity. The resemblance is indeed quite natural, if one - 106 - considers for a moment that fractions are simply quantities of different denominations.
The following illustrations elucidate the processes and require no lengthy explanations:
| ILLUSTRATIONS. | |||||||||||||||||||||||||||||||||
| Explanations.— The chain covers and shutters are placed, as shown in the cut, in order to reserve places for shillings and pence. The amounts are then registered in the regular way, and the resulting totals are reduced by deducting the next lower multiples of 12 and 20; by placing these complementally and adding the quotients in the respective columns. Spaces for a gross total of 999 pence and 999 shillings are provided for which covers all practical requirements. This method makes the addition of pounds, shillings and pence as simple as that of dollars and cents, the reduction at the bottom of the page being practically instantaneous, if the operator has any experience with English currency. | ||||||||||||||||||||||||||||||||
| The figures of the subtrahend are placed complementally, the wheel shutter between the bu. and lb. columns covering up the 1, which appears in the indicator. The 1 in front of the difference in the but columns is either ignored or eliminated. In case the number of lbs. in the minuend should be less, add first the number of lbs. contained in a bushel, and register the bu. of the subtrahend, according to the left-hand complemental scale, to allow for the 1 which has to be carried. | ||||||||||||||||||||||||||||||||
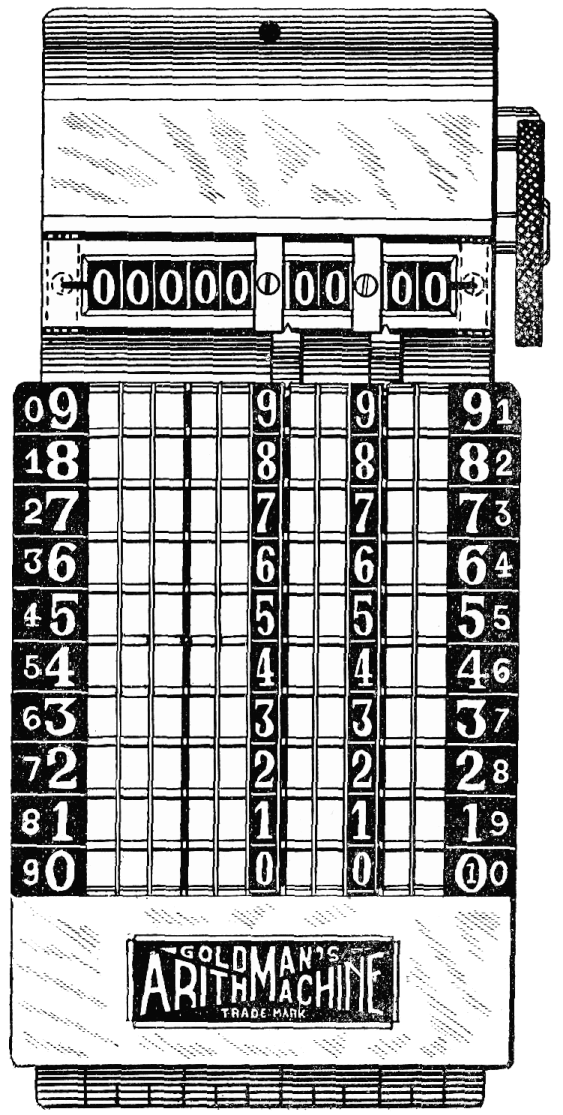
Capacity. 999,999,999.99
Actual size.
| 3. Insert the chain-cover and shutter over the third column and register. first the product of 23 by 4 in the ft. columns; then of 11 by 4 as inches, reducing as you proceed, then of 23 by 8, and 11 by 8 as inches, dividing the last product by 12 before placing it on the machine. By deducting 12 from the sum in the in. columns and adding 1 to the ft. columns, the correct result appears in the indicator. |
Denominate quantities may also in many instances be advantageously reduced to decimals, and can then be manipulated like whole numbers, which greatly simplifies the process of Division.
NOTE.— It may be new to some that one cannot multiply dollars and cents by dollars and cents, which is nearly as absurd as taking four apples three pears times.
Miscellaneous Computations.
The natural limitations of this work do not allow us to explain in detail the many practical applications of the basic processes of arithmetic for the different commercial, educational and scientific requirements. We will briefly touch upon a few, each representative of a class, and giving some idea of the broad field of usefulness of mechanical computation. Problems of percentage are, perhaps, the most frequent, and among these the addition of a certain per cent of profit to a cost price, the computation of interest on a note, or the figuring of discounts are of constant occurrence. The Arithmachine assists in performing any and all of these processes, and a few examples will serve to fully demonstrate its utility.
- 109 -ILLUSTRATIONS.
| 1. Cost price | $1.54 | , profit 33⅓ %; selling price? |
|---|---|---|
| ⅓ | 51 | |
| ---- | ||
| $2.05 | Answer. |
The simple registration of the cost price and profit gives the result. The addition is performed simultaneously by the Arithmachine.
| 2. | $546.23 | for 3 mos. 14 days, at 6%; interest? |
|---|---|---|
| 9.10 | ||
| 36 | ||
| ---- | ||
| $9.46 | Answer. |
Five straight and short movements of the stylus, performed in less than three seconds by one familiar with the rule, produce the result.
| 3. Amount, | $45 23 | ; discounts, 50, 10 and 5%; net? |
|---|---|---|
| 22.62 | ||
| 20.36 | ||
| $19.34 | Answer. |
Not more than 12 figures need be placed on the Arithmachine to give the correct answer, an effort conveniently performed in half the time required by the pencil methods.
The shortest methods of computing interest and discount, partial payments, present worth, compound interest, premiums and annuities, foreign exchange, arbitration, investments, etc., are contained in Goldman's "Short Methods for Computing Interest and Discount," to which those who wish to post themselves thoroughly in this direction are referred. The Arithmachine will also prove of considerable assistance when interest and discount tables are employed, performing all the incidental additions as fast as the amounts can be read, and doing away entirely with the use of pencil or paper in this connection.
- 110 -NOTE.— Smith's, Preston's, Dean's, Clarke's, etc., are among the best interest tables, and for compound discounts we can recommend Ladd's Discount Book, Jennings' Discount Tables and the Combination Discount Calculator.
Another class of computations, often needed and rarely understood, is that, referring to the averaging of accounts, equation of payments, accounts current, etc. The Arithmachine can be advantageously employed to perform all the operations connected with these computations, and Goldman's "New Method of Averaging Accounts," etc., presents the latest and best methods of solving problems of this kind.
Powers and Roots.
To raise a number to the 2nd, 3rd, 4th, 5th, etc., power, the following formulas will serve in the place of lengthy instructions, a and b representing the figures of which the number is composed, a being supposed to represent tens with reference to b. The arrangement of the results is somewhat different from that generally found in algebraical text books, but is believed to be better adapted for use in connection with the Arithmachine. The exponents not only indicate the powers to which the different figures of the number must be raised, but at the same time the number of places which must be reserved for the partial results. From this it is readily inferred that the 2nd power of a number, composed of two figures, cannot contain more than four places, the 3rd power not more than six, the 4th power not more than eight, etc.
- 111 -FORMULAS.
| 2nd | Power: | (a+b)2 | =a2+b2+2ab |
| 3rd | " | (a+b)3 | =a3+b3+3a2b+3ab2 |
|---|---|---|---|
| 4th | " | (a+b)4 | =a4+b4+4a3b+6a2b2+4ab3 |
| 5th | " | (a+b)5 | =a5+b5+5a4b+10a3b2+15a2b3+10ab4 |
| etc. | etc. | etc. |
| ILLUSTRATIONS. | EXPLANATIONS. | |||||||||||||||
| 1. Place the squares of 4 and 7 in the indicator, allowing two places for each. Then register the product of the two figures repeatedly in the second place, and the complete answer is obtained. | |||||||||||||||
| 2. Place the cubes of the two figures in the indicator, allowing three places for each. Then register in the third place the product of the square of the first by the second figure three times, and in the second place the product of the first figure by the square of the second figure three times, and the result appears in the indicator. | |||||||||||||||
The same methods can also be applied to larger numbers, and higher powers may be obtained by multiplying those of a lower order, the second and second producing the fourth, the second and third, the fifth, etc. A number containing two decimals exhibits four in the second power, six in the third, etc.
To extract the second, third, fourth, fifth, etc., root of a number the following formulas will suffice to point out the process, a representing the figure of the root already found, and b the next figure to be ascertained, also remembering that a is to have ten times the place value of b. The number must be separated - 112 - from the right to the left into periods, and the highest exponent of a indicates also the number of figures in each period.
FORMULAS.
| 2nd | Power: | (a+b)2 | =a2+b2+2ab |
| 3rd | " | (a+b)3 | =a3+b3+3a2b+3ab2 |
|---|---|---|---|
| 4th | " | (a+b)4 | =a4+b4+4a3b+6a2b2+4ab3 |
| 5th | " | (a+b)5 | =a5+b5+5a4b+10a3b2+15a2b3+10ab4 |
| etc. | etc. | etc. |
| Explanation.— Place the given number in the indicator, leaving one place vacant to the left, and part it in periods of two figures, with the aid of wheel shutter and decimal point. The first figure being 4, its square root is 2, which, registered twice complementally, produces 20, the 2 of this sum being the first root figure. Consider the next period, 45, and form the trial divisor to the right, by doubling the first root figure 2 and annexing 1, indicating how often 41 is contained in 45. By registering 41 complementally as 59, the next root figure 1 and the remainder 04 are obtained. Bring down the next period 21, double the number expressed by the first and second root figures, annex 1, which indicates how often 421 is contained in 421, and register this number complementally as 579, which produces the 3rd figure of the root and leaves no remainder. It must be remembered that all these processes appear in the indicator of the Arithmachine in a single line, the given number being registered to the left and the trial divisors to the right. If preferred. especially in extracting higher roots, or when operating on larger numbers, the trial divisors can be placed on the erasable tablet or on a separate sheet. |
Whenever it is desired to obtain a larger number of decimals, ciphers can be annexed, - 113 - according to the limit of capacity of the machine employed. About as many more places as have been computed by the regular method can be ascertained by simple division of the last remainder by the last trial divisor.
The method of extracting square roots by registering successively the odd numbers 1, 3, 5, 7, 9, etc., complementally until the largest square contained in the first period has been deducted, is too cumbersome for practical use. Supposing the first period to be 83, it would require the complemental registration of 1, 3, 5, 7, 9, 11, 13, 15, 17, in place of the simpler process of registering 9 times 9 complementally, which is equivalent to 9 times 1 or 9, which added to 83 produces 92, the root figure 9 and the remainder 2. The above method is based on the fact that in the series of the odd numbers: 1, 3, 5, 7, 9, 11, etc., the sum of the terms is equal to the square of the number of terms.
| 12 | 1 |
| 22 | 1+3 |
| 32 | 1+3+5 |
| 42 | 1+3+5+7 |
| 52 | 1+3+5+7+9, etc., etc. |
NOTE:.— In the series of the even numbers, 2, 4, 6, 8, 10, 12, 14, etc., the square of the number of terms, increased by their number, equals the sum of the terms.
| 12+1 | 2 |
| 22+2 | 2+4 |
| 32+3 | 2+4+6 |
| 42+4 | 2+4+6+8 |
| 52+5 | 2+4+6+8+10, etc., etc. |
| ILLUSTRATION. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Explanation.— In the above illustration the result is recorded in the erasable tablet, while the computation of the trial divisor can be performed on a separate Arithmachine or an extra sheet of paper. The 11-column Arithmachine is particularly adapted for problems of this kind.
For extracting higher roots the methods employed in manual arithmetic may be utilized, with slight modifications, in connection with the Arithmachine. The fourth root can also be ascertained by extracting the square-root of the square root, the sixth root by extracting the square root of the cube root, etc.
Logarithms.
The Arithmachine is splendidly adapted for the performance of all logarithmic and trigonometric computations. In order to utilize its capacity to the fullest extent, it may be desirable not to register the characteristic, but only the mantissa of the logarithms to be operated upon. The movable decimal point and sliding shutter will prove of great assistance, - 115 - while double complemental scales will be found a indispensable feature in this connection.
ILLUSTRATION.— Express the circumference of the globe in inches, knowing its radius to be 3,958 miles:
| Radius of the globe in miles | 3958 | 3.597486 |
|---|---|---|
| Relation of radius and diameter | 2 | 0.301030 |
| Relation of diameter and circumf. | 3.141593 | 0.497150 |
| Feet contained in a mile | 5280 | 3.722634 |
| Inches equivalent to a foot | 12 | 1.079181 |
| ————————— | ||
| Answer, 1,575,690,000 in. | Total, | 9.197481 |
Explanation.— The logarithms of the given numbers are taken from the tables and immediately registered on the Arithmachine, which simultaneously accomplishes their addition. As soon as the sum is ascertained, the corresponding numerus is found in the table.
The subtraction of logarithms, another frequent requirement, is performed by simply registering the subtrahend complementally on the Arithmachine.
There are two systems of logarithms in use — the hyperbolic or Napierian system, the base of which is 2.718281828, and the common or Briggean system, generally employed for practical purposes, the base of which is 10. The best logarithmic and trigonometric tables are those by Schloemilch with 5 places, Bremiker's with 6 places, G. von Vega's with 7 places, Callet's with 8 places of decimals, while the more accurate astronomical calculations require 10 place logarithms, and as a natural consequence Arithmachines of at least 11 column capacity. Gaussian logarithms, named after the German mathematician Karl Friedrich Gauss, are intended to facilitate the finding of the logarithms of the sum and difference of two - 116 - numbers, and are often designated as addition and subtraction logarithms.
We cannot attempt in the limited space at our command to give any instruction in the use of logarithms, but simply desire to point out the utility of the Arithmachine in this connection.
Correction of Mistakes.
The mere placing of the stylus point in any subdivision of the chain board, or its depression even, produces no change in the indicator; therefore if a mistake is noticed before the forward movement of the chain has been started, this initial step to the registration of a figure may be entirely ignored. This point represents a great advantage over other computing machines, where the slightest touch of the operating mechanism results in a derangement of the register. In the Arithmachine the chains, forming the operating surface, are locked, and only the deliberate effort of the arithmachinist can set them in motion, so that an error can even be corrected "before it is made."
If, however, the placing of a figure has actually been commenced, viz., if the chain has changed its position, it is safest and best to complete the stroke and to employ one of the following methods of correcting the mistake:
If a mistake has been made in placing a figure and noticed at the time, it can be speedily corrected by adding or deducting the differ-
NOTE.— The correcting of mistakes during the very act of placing a figure, while possible with special care, is not recommended.
- 117 -ence between the correct and wrong figures to or from the figures next to be registered in the same column.
To remove a figure from the indicator, which is equivalent to erasing it, place the figure complementally in the same column, and complete the process by registering ciphers (nines), according to the small left-hand scale to the left of the figure in question.
| Explanation.— The registration of the complement of the figure to be removed and of complemental ciphers to the left of it, has the same effect as deducting the figure from the amount which appears in the indicator. |
To increase a figure in the indicator add the desired difference in the corresponding chain column, and to decrease a figure in the indicator place the desired difference complementally in the corresponding chain column and register complemental ciphers (nines) to the left of it, according to the instruction above given.
To remove two or more figures from the indicator, register the desired figures complementally in the corresponding chain columns, according to the instructions given, and place complemental ciphers to the left of them.
| Explanation.— To remove the figures 7 and 8, register 78 complementally and place complemental ciphers to the left of them. | |||||||||||||||||||||||||||||||||||||||||||||
NOTE.— This process can be shortened by placing the wheel shutter over the first unoccupied place in the indicator, and stopping the registration of complemental ciphers (nines) as soon as the corresponding chain column is reached.
- 118 -To remove an amount entirely from the indicator, set the Arithmachine to zero, which is desirable in all cases when more than three figures are to be removed or corrected.
Machine Proofs.
A thoughtless argument against the adoption of computing machines is that the results obtained by mechanical processes are not proved to be correct. When a bookkeeper has completed the mental addition of a long column of figures he is certain of one thing, and that is that he does not know whether the total is right or wrong. He generally repeats the work in the opposite direction, and if he finds the same result, well and good, if not he is in a "muddle." In neither case is there any mathematical certainty with regard to the accuracy of the work. If the Arithmachine saves time and labor and mental strain in the first operation, it is self-evident that it will also do so in the second, with this advantage that there is much less liability of repeating a mistake on the machine than in mental computation.
But while the repetition of the process is still employed by many as a means of verifying results, there are a number of methods for proving computations, known as "check-number methods," which are much more rapid and at least as reliable, and which are well adapted for use in connection with the Arithmachine, by reserving the two left-hand columns of the machine for proof-work, and registering the check-numbers simultaneously with the given amounts or separately. These methods are - 119 - fully described and illustrated in a separate pamphlet, entitled "The Arithmetical Detector," which explains all known check-number methods thoroughly, and besides contains many applications which are entirely new and original with the author.
When taking off trial balances the Arithmachine can be employed to perform all the additions and subtractions in the ledger accounts, as well as the drawing off of balances, and in all cases where a trial balance containing the names of the accounts is not required the Arithmachine will serve as a means of proving the ledger, by registering the balances on the machine and proving every section of the work with the aid of Goldman's Advanced System for Locating Errors, which is now successfully employed by thousands of bookkeepers throughout the United States and Canada, who have either secured the complete knowledge from the author and his duly appointed representatives, or some imitation or adaptation through traveling or resident impostors. This system, with many recent improvements, is extensively treated in a copyrighted work published by the inventor, and those who are not in possession of it will do well to secure it, if at all interested in the subject. We particularly warn our readers against a number of book pirates, North and South, offering this system in incomplete form, or some impractical variation of it under fantastic titles, and by making false claims or promising catch prizes, try to entrap the unsuspecting - 120 - and to appropriate the results of our labors.
Speed Drills.
It will, perhaps, appear somewhat out of place that the chapter bearing this title is presented in the last pages of this work. A good excuse, however, is found in the fact that all a book can possibly accomplish is to convey useful information and to give practical directions, and that the attainment of speed depends almost wholly upon individual qualification and application, over which neither the author nor the book have any control. Furthermore, the first considerations in the study of Mechanical Arithmetic or any other science are the acquisition of facts and the mastery of principles, while the attainment of speed is something which does not belong to the science itself, but rather to the art of applying it.
In comparing the speed attainable on the Arithmachine with that of mental or manual arithmetic, the following facts will demonstrate the advantages of Mechanical Arithmetic. In addition the mental carrying as well as the combining of different figures into one sum are saved and the danger of mistakes in performing these operations avoided. In subtraction the mental process, of ascertaining the differences as well as the carrying and borrowing, with their accompanying liability to error, are removed. In multiplication the mental carrying and adding of the partial products are done away with, the machine performing all processes simultaneously. In division the multiplications - 121 - of the divisor by the quotient figures as well as the subtraction of the products, are performed at the same time. Besides the mental and manual effort of writing or forming the figures is practically avoided, the motion of the hand and fingers being equivalent to that of forming the figure 1, the simplest and most rapidly executed of all digits. The length of the stroke makes little difference within certain limits, as one can draw straight line of 1/4, 1/2, 1 or 2 inches in about the same space of time. The machine also saves the registering of all ciphers, which in ordinary columns represent about 20% of the work, being employed to indicate the place value of the significant figures. For instance, $2,003.50 is placed with three strokes on the Arithmachine.
To attain speed and precision in operating the Arithmachine the following fundamental rules must be invariably and scrupulously adhered to:
- Depress the stylus point fully, to insure the free and easy movement of the chain.
- Hold the stylus vertically, to prevent friction with the partitions and to preserve the proper alignment of the chain links.
- Look ahead while completing a stroke, so that not a moment's time will be wasted in finding the place for registering the next figure.
These rules are very easily observed and as soon as the correct habit of manipulating the Arithmachine is formed, they will be almost instinctively complied with.
In addition to these rules, a few, practical suggestions will prove of value:
- 122 -- Always consider a number or amount as a whole, which is to be placed continuously, to avoid the delays occasioned by repeatedly referring to the blank book page etc.
- Keep the next item or number to be registered in full view, so that the eye becomes accustomed to reading the figures, while the hand goes through the mechanical process of pulling the stylus point.
- See that neither the Arithmachine nor anything else covers the figures to be operated upon, holding the example clearly before you, either in your mind, on paper or on the erasable tablet attached to the machine.
When performing addition, the most frequent and important of all arithmetical operations; try to take single amounts in one mental grasp, and two or more if practicable. Combine these items into one, whenever this can be accomplished without mental strain. For instance: $345.00, $5.00 and 75 cents can be easily and quickly combined and $350.75 registered. This will increase the operator's speed wonderfully, and besides develop one's mental alertness, fully as useful as the mental aptitude at figures in general, and much less straining. The greatest advantage of the Arithmachine will become apparent in very long and heavy columns, as the carrying of figures is entirely avoided, all columns being added simultaneously, and the liability to error materially decreased.
NOTE.— The Arithmachine could also be operated with two stylus points, the one placing a figure while the other takes its position for registering another,
- 123 -
One of the most important elements in the
acquisition of speed is a thorough knowledge
 of the chain-board. The accompanying illustration gives the imaginary appearance of the
chain-board, the location of the
figures and the distinction of
the columns, which must become so familiar to the operator
that any desired number, can
be instantly placed, without
reference to the numeral scales.
A very helpful drill adapted
for this purpose consists in
repeatedly and systematically placing the same
figures in different columns, commencing with
the row of ones and proceeding to the row of
nines and vice versa, and then registering the
different figures in the same columns, commencing with the one and proceeding to the
nine and vice versa, and going from the first
column to the eighth and back again to the
first.
of the chain-board. The accompanying illustration gives the imaginary appearance of the
chain-board, the location of the
figures and the distinction of
the columns, which must become so familiar to the operator
that any desired number, can
be instantly placed, without
reference to the numeral scales.
A very helpful drill adapted
for this purpose consists in
repeatedly and systematically placing the same
figures in different columns, commencing with
the row of ones and proceeding to the row of
nines and vice versa, and then registering the
different figures in the same columns, commencing with the one and proceeding to the
nine and vice versa, and going from the first
column to the eighth and back again to the
first.
Another exercise, quite as serviceable, is to register certain amounts containing a variety of figures, such as 243.59, 647.81, etc., 10, 25 or 50 times in succession, or to perform a given example repeatedly, and to note the time it required to complete the task. In trying to attain proficiency, however, accuracy and precision should never be sacrificed on the altar of speed, as it is evidently much better to obtain a correct result in ten seconds than to arrive at two wrong ones in half that time.
There is practically no limit to the speed with which the Arithmachine can be operated, - 124 - as the mechanism responds to the most rapid movement of the hand. Everything depends upon individual skill and alertness. The record of one operator may be easily broken by another, and a few months' practice will develop operators of such a degree of proficiency as to enable them to make a profession of operating the Arithmachine and secure a handsome income as arithmachinists. For not only in the service, of other firms, but also in the interest of spreading the adoption of the Arithmachine, exceptional opportunities will be offered to those who have become expert in its operation, and it is our intention to encourage practice and development by arranging from time to time speed contests with cash, prizes for expert manipulation, to which Arithmachinists in all parts of the United States and Canada will be admitted free, and, by a novel plan of competition, without leaving their own home or locality. Particulars will be cheerfully furnished by the author to all who wish to participate in these prize contests.

CONCLUSIVE.
COMPUTING machines in general occupy a unique position in the mechanical world in this particular, that they are practically the only appliances intended to perform brain work, and the Arithmachine takes an exclusive place among computing machines, being the first and only mechanism ever invented, possessing the essential requirements of a practical and popular device of this kind. It is confidently believed to mark a new era, not only in the construction of arithmetical machinery, but also in the instruction in practical arithmetic, demonstrating the commercial and scientific importance of Mechanical Arithmetic, and making its wider dissemination and adoption possible.
The substitution of matter for mind, of physical force for mental energy, the utilization of space to save time and labor, form the characteristic features and advantages of a practical computing machine. The Arithmachine possesses these features and gives these advantages in a higher degree and to a greater extent than any other computing device known at the present time. It saves time because it carries any desired number of columns simultaneously, responds to the slightest impulse of the hand, does away with the placing of ciphers entirely and registers the results as fast as numbers can be read. It saves labor because it relieves the mind of all straining effort, and the hand of the nerveracking depression of keys.
It is claimed by those interested in key computing machines that these are superior to any operated by other means, stating by comparison that the key typewriters are considerably in advance of the single-hand writing machines. But the analogy is lame. In adding long columns, for instance, it is not practicable to fix one's eyes upon the keys and to use both hands in striking the keys, but, to avoid omissions, repetitions and - 126 - other mistakes, it is necessary to employ one hand as a guide to the figures, which therefore becomes useless in operating the machine. Taking into consideration the delay and annoyance and mental strain occasioned by the continuous change of the field of vision from the keyboard to the figure column and vice versa, and the ground which has to be traveled over by the fingers of both hands in different places, it becomes evident that the fancied superiority or claim of superiority of the key computing machines, by which we mean those of considerable proportions, carrying all columns simultaneously, is based upon a fallacy. In fact, practice demonstrates more than arguments that a compact and efficient mechanism, like the Arithmachine, which permits the simultlaneous observation of the operating surface and figure columns, which avoids the constant twisting of the head or moving of the eye, which does not require the going over a wide space by the eyes or fingers, which does away with the noise and rattle characteristic of all key machines, and so objectionable at the accountant's desk, and which relieves the nervous strain caused by the constant pounding of the fingertips by the keyboard or vice versa, not to mention other advantages, as difference in price, size, weight, etc., is much more desirable and effective for general office use, than the high-priced and heavy weight devices. While it is possible that one operating these for a long time, keeping in continued practice and doing nothing else, could attain slightly greater speed than is practicable on a really practical machine, the fact remains that the Arithmachine is better adapted for 99% of the work which is required of a computing machine, that it can be much more rapidly mastered and with much less practice than is required by the key machines, in order to attain even ordinary speed. Furthermore the delays occasioned by excessive size and weight, the getting ready for work, etc., being removed, the Arithmachine more than matches the key machines as a labor saver, while eclipsing them altogether, when convenience of manipulation, lightness, noiselessness and cheapness are taken in consideration.
In the key-operated machines every key must be depressed separately, distinctly and until a hard bottom is reached, in order to properly actuate the carrying mechanism, - 127 - which permits only the use of a single finger at a time, and the multiplicity of figures (144 in the eight column machines), and the continuous vibration or banging of the keys, are serious obstacles to the attainment of the greatest speed. In the Arithmachine all these conditions are changed. An operating surface of 2½ square inches takes the place of a large area of keys. The "touch" of the Arithmachine is light and elastic, the movement of the chains easy and natural, and the eye always rests upon a surface in complete repose, which greatly assists in selecting the place for the next figure to be registered. In the key listing machines, a lever or crank and printing mechanism must be operated in addition to the manipulation of the keys, while a listing Arithmachine could easily be constructed, avoiding these objectionable features, should the demand justify its manufacture on a large scale.
A few imagine that the Arithmachine being small in size and light in weight, ought not to cost more than the different toy devices now offered to the public under the name of adding or computing machines. But the fact is generally lost sight of that there is no other computing machine known which accomplishes as much, and that not quite as satisfactorily, which is offered for less than five times the price asked for the Arithmachine. It costs time and money to construct a mechanism of the quality and accuracy of the Arithmachine, and its small size, which is one of its most important features, if considered from a practical standpoint, is at the same time an element of considerable expense. In fact it would be much cheaper to build it twice its present size and weight, which, perhaps, would make it appear more precious to those who judge the value of a computing machine by its outside dimensions. But a Waterbury watch costs less than a fine Elgin or Waltham movement, and a large alarm clock can be bought for fifty cents.
The fear, entertained by some, that the introduction of a really practical computing machine, would have a tendency to decrease the mental ability of operators, somewhat resembles the misgivings expressed in former days that the invention of the steam engine would result in the shrinking of the muscles of civilized man. But - 128 - just the reverse is true. Mechanical Arithmetic judiciously applied has a tendency to enlarge the intellectual capacity of those who become conversant with it, by economizing their mental strength and saving it for work requiring a keen and alert intellect, not one dulled by the drudgery of figures, and by avoiding the wear and strain generally connected with long and tedious computations. And while it may please some noble souls to see others struggling with figures, there is really nothing elevating or satisfying in footing fifty or a hundred pages, "sixty lines deep and six figures wide."
Our expectations, that a computing machine, possessing the desirable qualities of ours, which is free from the detects of others, will be favorably received by the commercial and scientific world, are already commencing to be realized. Words of praise, and the more palpable kind of encouragement which is expressed by the short and significant word "orders," have come to us from every part of this continent and even from foreign countries, and while we do not expect everybody to buy a machine on sight of a circular (which would tax our manufacturing facilities to the utmost), we are convinced that the truly progressive will be glad to avail themselves of its time and labor-saving services, while the "old fogies," who, like the poor, will always be with us, will sooner or later fall into line - in self-defence. Of course, an invention which is likely to change acquired habits and accustomed methods is bound to meet with opposition. When railroads were first introduced the good owners of horses and wagons warned against accidents, and the typewriter was ridiculed by nearly every penmanship teacher in the land. Some will oppose the Arithmachine because it may throw bookkeepers, etc., out of employment; but as long as the machine operating the machine is not forthcoming, no serious misgivings need be entertained on this account. Railroads, telegraphs, telephones, typewriters, etc., have made a civilization possible which furnishes positions to thousands where formerly hundreds were employed, and a practical computing machine will, open new channels of employment to many, who otherwise would be entirely debarred from arithmetical work!
- 129 -ANNOUNCEMENTS
We append in the following pages a limited number of selected
advertisements, which are likely to prove of special interest to all
who desire to keep posted regarding office improvements. They
represent to a considerable extent the leaders in and originators
of advanced office methods, and reflect the progress made in this
direction. Furthermore, the firms represented are all responsible
and reliable, and will perform every contract as agreed, and
execute every order promptly and satisfactorily, which is in itself an
illustration of modern business conduct.
[Note that the majority of the ads are
for Henry Goldman's own products, often through his company
The Office Men's Record, and several other ads are for companies
that are located in the same building or very nearby.]
THE PUBLISHERS.
 INDEX
INDEX 
|
|
Mention Arithmachinist when placing Orders or making Inquiries.
THE KAOLIGRAPH

|
is a negative duplicator, having neither glue nor gelatine in its composition. Is not affected by heat. Negative can be removed from surface with a few touches of wet sponge. Copies do not curl up. Has great lasting qualities. Easily kept level. For reproduc- ing 10 to 50 duplicates, cheaply, cleanly, and with minimum amount of labor, it has no superior. Prices with supplies, deliv'rd: 6x10, $3.00; 10x12, $4.50; 10x15, $6.00. Refilling half-price. Larger sizes in stock. |
| CHAS. W. BIRD, 358 Dearborn Street, CHICAGO. | |
| Without desire to profit by the misfortune of others, we deem it polite to say—with the utmost delicacy, however—that in the un- toward event of your being compelled to purchase |
| TYPEWRITER SUPPLIES, |
| RIBBONS, CARBONS, |
| LINEN PAPERS, ETC., ETC. |
| THE VERY BEST CAN BE FOUND AT |
| JOHN UNDERWOOD & CO.'S |
| 163 S. La Salle Street, Chicago. |
| IMITATION TYPEWRITTEN LETTERS. | FORM LETTERS. CIRCULAR LETTERS. |
| You no doubt use Form Letters at various times. Have you ever tried circularizing with imitation typewritten letters? There is no advertising you can do that will pay better. A trial will quickly con- vince you. Advertising by this method is cheap, but effective, if your list is good. Every letter goes to some interested party. There's no random firing; no waste of circulation. Perhaps that's why it pays. Have you tried it? The cost is small. Business men are great users of our imitation typewritten Circular Letters. We turn them out by the thousand or million, in any style typewriter type, at extremely low prices. Letters by our process are perfect and answer as if each were written separately. Our list of customers includes the names of hundreds of Business Firms throughout the U. S., and if low prices and superior service will secure us your trade, we will, after you have seen our work and prices, surely also number you among our clients. Samples are free. Write today. CHAS. E. FOYER CO., 96 Fifth Ave., Chicago. | |
| Capacity, 50,000 per Day. | |
| OFFICE | WANTS, | ADDING MACHINES, CHECK PROTECTORS, FOUNTAIN PENS, INK- STANDS, LETTER FILES, etc., Supplied at Lowest Prices. Catalogue 10 |
| cents. Postpaid. Address, THE OFFICE MEN'S RECORD CO., Roanoke Building, CHICAGO. | ||
| PROFITABLE | EMPLOYMENT | FOR BOOKKEEPERS during Leisure Hours. No Soliciting. For Particulars write: |
| HENRY GOLDMAN, INVENTOR, 145 LA SALLE ST., CHICAGO. | ||
Mention Arithmachinist when placing Orders or making Inquiries.

|
| RUBBER STAMPS |
| Of All Kinds. |
| NOTARY AND CORPORATION SEALS. AUTOMATIC NUMBERING MACHINES. |
| Badges, |
| Stencils, |
| Steel Stamps, Etc. |
| SEND FOR CATALOGUE. |
| CHAS. L. SAFFORD, |
| 175-181 Madison St., - Chicago |
| Telephone Main 2057. |
- 132 -
 |
||
| (Copyright, 1895, by The Office Men's Record Co.) | ||
| FROM time to time there appeared in the columns of the Office
Men's Record, original methods and articles on subjects of
Accounting, Practical Arithmetic, Penmanship, Shorthand, Commer-
cial Law, etc., the value of which, and the interest in which are of a
permanent nature. But our supply of back numbers has become
practically exhausted, and we decided upon the publication of these
selected contributions in a handy and separate form, which we give
the characteristic and significant title, OFFICE TRACTS, their
mission consisting in spreading valuable and practical information
and increasing the usefulness and ability of those who peruse them.
The low price of these pamphlets, however, does not begin to express
their value, many a single contribution being worth a thousand times
its cost to those who take advantage of and apply the information
therein presented. It is our ambition to bring these Office Tracts
within easy reach of every Office Worker in the United States and
Canada. We have thus far completed the four numbers of Series I,
embracing the following subjects:
No. 1. Subtraction by Addition.
No. 2. Vertical Writing.
No. 3. Account Books as Evidence.
No. 4. Arithmetical Amusements.
It will be our aim to treat in each successive series a variety of
subjects, appealing to those who take an interest in lighter and
heavier themes, covering the different departments of interest to
office people, and making each number complete and exhaustive in
itself.
Sent, postpaid, to any address on receipt of 25 cents.
Single Numbers, 10 cents.
The Office Men's Record Co.
PUBLICATION DEPARTMENT,
143-149 La Salle St., CHICAGO.
| ||
- 133 -
 |
| COMPILATION |
| —OF— |
| NAMES AND ADDRESSES |
| —OF— |
| SPECIAL INTEREST TO OFFICE MEN, |
| Together with Other Valuable Information! |
| 15 CENTS A COPY. |
| The Office Men's Record Co., |
| 143-149, LA SALLE ST., CHICAGO. |
| BOOKS AND DEVICES | FOR OFFICE MEN |
| Will be sent to any address on receipt of publishers' or manufacturers' advertised prices. We also undertake to supply volumes which are not to be found in book stores, and appliances which cannot be secured through the trade. THE OFFICE MEN'S RECORD CO., 143-149 La Salle St, Chicago. | |
 Cut out parts at dividing lines.
Cut out parts at dividing lines. |
GOLDMAN'S Transformation PUZZLE. |
| Transform Square into Trian- gle with only two changes! Prizes for first ten Solutions! For Registry Particulars, Sample Copy of "Office Men's Record," World's Fair Souv- enir and instructive circular send 10 cents to | |
| The Office Men's Record Co. Major Block, CHICAGO. |
| Room 506, 145 LA SALLE STREET, (Roanoke Bldg.) CHICAGO, ILL. | SEC'Y & MANAGER, The Kent Anti-Forgery Co. | |
 |
Expert on Handwriting, Forgeries and Changes in Written Instruments. | |
| REFERENCES: | ||
| Lyman & Jackson, Attys., Chicago. | Otto Gresham, Atty., Chicago. Joseph Errant, Atty., Chicago. | R.S.Iles, County Atty., Chicago. Chas. S. Thornton, Corp. Counsel, Chicago. Judge James Shaw, Mt. Carroll, Ill. Fishback & Kappes, Attys., Indianapolis, Ind. A. B. Kittredge, Atty., Sioux Falls, South Dakota. | ||
| Established 1878 | |
| Wm. ZIMMERMAN | PATENT LAW. |
| Practices in all U.S. Courts | |
| on the law of PATENTS, TRADE-MARKS, DESIGNS, LABELS, COPYRIGHTS. Investigations and opinions on questions of in- fringement, validity, etc., of patents. SOLICITOR for United States and Foreign Patents, Trade- Marks, etc. Reliable correspondents in Washington and all prin- cipal foreign countries. | |
| 164 DEARBORN ST., CHICAGO. | |
| [Note that Zimmerman was witness on most of Goldman's patents, and most likely his patent lawyer.] | |
| NOTARY PUBLIC. | |
| I. D. CLARK, | |
| Mechanical Expert and Patent Office' Draughtsman | |
| Blue Prints and Validity Searches made . . . . . . . | |
| SUITE 1103-1104 | 352 Dearborn Street, CHICAGO |
| ADVERTISERS! |
| I design and write business bringing and space utilizing adver- tisements, intended to reach Office People. If you offer anything of merit, send me your circular or other data, accompanied by $2, and I will furnish you an advertisement which will "do the rest." Money saving suggestions regarding the selection of Mediums cheerfully given. Cards, Circulars, Folders, Pamphlets, etc., prepared at the low rate of $2.50 per page. A. D. CARPENTER, Care of The Office Men's Record Co., 143-149 La Salle St., Chicago. |
Mention Arithmachinist when placing Orders or making Inquiries.
- 135 -
| ADJUSTER OF FIRE LOSSES....... |
| ——————— PARTNERSHIP SETTLEMENTS. ——————— CORPORATION AND MANUFACTURERS' BOOKS Carefully Audited. ——————— BOOKS AND SYSTEMS OF ACCOUNTS ARRANGED For Any Requirement. ——————— PERIODICAL AUDITS Made at Very Reasonable Rates For Capitalists, Merchants, Manufacturers and Corporations. |
| WILLIAM FRIES, | |
| AUDITOR AND ACCOUNTANT | |
| 1017 New York Life Bldg. N. E. cor. La Salle and Monroe. | |
| REFERENCES: ✠ |
| Chauncey J. Blair, President Merchants National Bank. Bernhard Neu, Cashier International Bank. George F. Stone, Secretary Board of Trade. Edwin E. Hooper, Secretary Lumberman's Association. Stewart Spalding, Sec'y Calumet & Chicago Canal and Dock Co John Benhan, General Manager The Consumers Company. Charles Seegers, President American Varnish Co. Hon. Nathaniel E. Sears, Judge Appellate Court. Spaulding & Merrick, Wholesale Tobacconists. Arnold, Schwinn & Co., "World" Bicycles. |
- 136 -
| GOLDMAN'S |
| ADVANCED SYSTEM FOR LOCATING ERRORS |
| Without Re-checking or Copying Entries. |
| Copyright, 1890, by Henry Goldman. |
| WHAT IT DOES: |
|
| This is not a stale compilation of old and commonplace rules, which may or may not prove of service, nor a plan of subdividing the Ledger into artificial sections of 100 or 200 pages, nor a blank book scheme, necessitating a complete change of Ledger, Journal, Sales Book, etc., in order to gain a questionable advantage, but a simple and complete system, based on an entirely new and original idea, which accomplishes the seemingly impossible, requiring No Change of Book-Keeping, No Additional Books, No Carrying of Totals During the Month, No Special Division of the Ledger, No Copying of Amounts, No Slips or Forms of any kind, Etc., Etc. It removes all difficulties generally experienced with the Trial Balance, and without entailing extra labor, practically reduces the routine work of the Office, as all postings, footings and balances are proved without comparing amounts, re-checking or re-figuring. With its aid an itemized Trial Balance can be taken in half the time generally consumed by book-keepers, a great saving of time at a time when time is most valuable, avoiding entirely the delay in commencing the posting for the current month. Considering the importance of the information offered, the facility of its application, an the many advantages derived from its use, no intelligent and progressive book-keeper can afford to do without it. |
| Errors in Single-Entry Book-Keeping Detected with Equal Facility. References and Testimonials on Application. |
- 137 -
| The Arithmetical Detector. |
| Complete Systems for Proving Arithmetical Results Without Re-figuring. |
| PROOFS for Addition, Subtraction, Multiplication and Division of whole numbers, decimal or common fractions, saving time and work detecting and locating mistakes, preventing repeti- tion of the same error and guarding also against transpositions of figures. Equally applicable to Dollars and Cents; Pounds, Shillings and Pence; Bushels and Pounds; Feet and Inches, etc. Every known check number system thoroughly explained. Price, separ- ately, $1.-, Postpaid. |
| Short Methods for Computing Interest and Discount. |
| Simple Interest, Discount, Compound Interest. |
| ACCURACY and speed in computing interest and discount are important accomplishments: that they are so rarely found, proves to a great extent the deficiency of the methods hitherto introduced. The author offers in this work a method pronounced by experts as the shortest and simplest known, and leaving nothing to be desired. It can be easily acquired, and when once learned can hardly ever be forgotten. Being applicable in all cases which may possibly arise, it is bound to win its way into general use. More convenient than the use of tables. Simpler than the "60 Days Rule." Ordinary problems solved almost instantaneously and with- out mental effort. Improved Methods for Computing Bank Dis- count, Present Value, Partial Payments, Premiums, Annuities, etc. Price, separately, 50 cts., Postpaid. |
| New Method for Averaging Accounts. |
| Simple Average, Equation of Payments, Accounts Current. |
| SAVES one-half the Time, Work and Figures, compared with methods now in general use. Superior in principle and appli- cation to the so-called "12 per Cent. Rule." Absolutely cor- rect and adapted to all requirements. Equal or different Terms, Time or Discount. Simplified methods for closing an Account Cur- rent, and calculating Interest on Balances and Overdrafts. Price, separately, 50 cts., Postpaid. |
| Complete Instructions .. in my .. "Advanced System for Locating Errors," |
| "Short Methods for Computing Interest and Discount." "New Method for Averaging Accounts," Etc., |
| will be mailed to any address, postpaid, on receipt of price $10, which includes replies to all further inquires free of charge. |
| ———————— |
| HENRY GOLDMAN, |
| AUTHOR AND INVENTOR. |
| 143-149 La Salle St., - - - - - CHICAGO, ILL. |
| Avoid resident or traveling imitators. |
- 138 -
 |
| Locates Errors to Page and Account without referring to the Ledger, rechecking or copying en- tries. Easily applied without change. Request circular. HENRY GOLDMAN, Inventor, 145 La Salle St., Chicago. |
| Sent, postpaid, on receipt of $2.00. |
| Trial Lesson, 10 cts. Teachers desired everywhere.
Address for particulars,
PATERSON'S
|
 Properly directed, qualifies for Business!
Book-keeping, Penmanship, Shorthand, etc. quickly learned
without personal attendance. Advanced methods. Moderate
terms. Particulars free. Address: SELF-STUDY BUSI-
NESS UNIVERSITY, 504-505 Roanoke Building, Chicago.
Properly directed, qualifies for Business!
Book-keeping, Penmanship, Shorthand, etc. quickly learned
without personal attendance. Advanced methods. Moderate
terms. Particulars free. Address: SELF-STUDY BUSI-
NESS UNIVERSITY, 504-505 Roanoke Building, Chicago. |
Mention Arithmachinist when placing Orders or making Inquiries.
- 139 -
| For Bookkeeping Use | |||
| THOMAS' No. 9 WRITING FLUID. | |||
| For Ruling, | |||
| THOMAS' CRIMSON INK. | |||
| I N K S, M U C I L A G E, |  |
P A S T E AND G L U E, | |
| Use Thomas' Fountain Pen Ink | |||
| DOES NOT GUM THE PEN. | |||
| THOMAS' PASTE. | For Mounting Photographs and All Kinds of Pasting | ||
| ————————— | |||
| FOR SALE BY ALL STATIONERS | |||
- 140 -
| Telephone Main 5242. |
| CICERO HINE, |
| MANUFACTURlNG STATIONER, |
| PRINTER |
| and GENERAL |
| BINDER, |
| Blank |
| Book |
| Maker, |
| OFFICE: |
| 215 DEARBORN STREET, |
| Chicago. |
| H. W. HINE, Agent. |
| When needing Blank Books or Printing let us figure with you. |
- 141 -
| Highest Awards, Diploma and Medal, World's Fair, 1893 GOLDMAN'S IMPROVED —————————————— Self-Checking TRIAL BALANCE BOOK (Copyright, 1890 and 1891, by Henry Goldman) | |
| IMPROVED IN QUALITY | REDUCED IN PRICE |
| FACILITATES THE FINDING OF MISTAKES! ORIGINAL FEATURES | |
| DOUBLE LEAVES—Bring names and amounts closely together, and save re-writing of names. GUIDE NUMBERS—Prevent writing balances in wrong lines, by guiding the eye across the page. TRANSFER COLUMNS—Permit the carrying of balances on the same line for an entire year. FOLIO INDICATORS—Assist in making quick and immediate reference to any desired account. SUMMARY SHEETS—Avoid the carrying forward or recapitulating of totals. CHECK COLUMNS—Avoid the crowding of amount columns with check marks, and assist in locating errors in connection with "Goldman's Check System." | |
| FOR SALE BY THE OFFICE MEN'S RECORD CO. Business Office Specialists, 143-149 La Salle St., CHICAGO, ILL. | |
| When ordering through Stationers, be sure to specify GOLDMAN'S IMPROVED SELF-CHECKING TRIAL BALANCE Books. Absolutely Refuse Substitutes. If orders are placed with us, we prepay ex- pressage. Descriptive Sample Booklet sent free on request. Order now to avoid the delay incident to the rush of the blank book season. We enter advance orders for delivery on any specified date. | |
- 142 -
| ALL WHO USE | |
| GOLDMAN'S | ADVANCED SYSTEM For Locating Errors, |
| whether the Original, taught by the Author, or an Infringement, palmed off by Impostors, can increase its effectiveness tenfold, with- out any noticeable additional effort, by adopting the Decimplex Improvement or Double Check. Full Particulars free. | |
| HENRY GOLDMAN, Author and Inventor, 145 La Salle St., CHICAGO, | |
| If you issue Checks YOU NEED........ |
| Thomson's Deposit and Check Journal The Most Satisfactory Means of Handling an Active Bank Account. Send 10c. for Full Sized Sheet, with Explanations. ———————— WALTER THOMSON, Albany, N. Y. |
|
It's easy when you know how |
|
Mention Arithmachinist when placing Orders or making Inquiries.
| National Cabinet Letter Files | |
 |
Made exclusively under patents by P. F. PETTIBONE & CO, CHICAGO, SUCCESSORS TO JOHN MORRIS COMPANY. |
| Do not confound us with the National File and Index Co.
or ANY ONE ELSE claiming to make "National"
Files. We have been making National Files since 1876.
Over 200,000 of our make now in use. | |
- 144 -
ALMOST ALIVE!
 Enables the user to draw straight or parallel lines of any desired
length, does not slip or move irregularly, and can be conveniently
carried in the vest pocket or rolled over a blank book page.
Enables the user to draw straight or parallel lines of any desired
length, does not slip or move irregularly, and can be conveniently
carried in the vest pocket or rolled over a blank book page. |
| Maple Wood, 25 cts.; Hard Rubber, 50 cts. |
| Sent, postpaid, to any address on receipt of price. |
| The Office Men's Record Co., |
| 143-149 LA SALLE ST., CHICAGO. |
| H. S. KELSEY | A. W. GORE. |
| KELSEY & GORE, | |
| OPTICIANS. | |
| 44E Madison Street, | CHICAGO. |
| HERMAN KOENIG | |
| DIE SINKING AND ENGRAVING, MEDALS, JEWELER'S DIES, CRESTS, COATS OF ARMS, FINE WAX SEALS, DIES AND RELIEF WORK FOR ALL PURPOSES. | |
| 358 Dearborn Street, | CHICAGO |
- 145 -

- 146 -
| The Underwood Typewriter | ||
| A thoroughly Practical, Visible Writing Typewriter |  |
Unequaled for Speed. Ease of Operation and Durability |
| FOR SALE BY Wagner Typewriter Co. 528-529 The Temple 184 La Salle St., CHICAGO, ILL. | ||
THE BLICKENSDERFER TYPEWRITER
 The only high-grade writing machine sold at a low price
No. 5, $35. No. 7, $50
Interchangeable type: no ribbon; permanent alignment;
unlimited speed.
For circular and samples of work, address
W. J. BLICKENSDERFER & CO.,
The only high-grade writing machine sold at a low price
No. 5, $35. No. 7, $50
Interchangeable type: no ribbon; permanent alignment;
unlimited speed.
For circular and samples of work, address
W. J. BLICKENSDERFER & CO., | |
| 195 a Salle Street, - | - CHICAGO, ILLS. |
- 147 -
 |
| Wyckoff, Seamans & Benedict, 144 Madison St., |
| CHICAGO. |
- 148 -
| ONLY SEWING MACHINE MADE |
| WITH BALL BEARINGS |
 |
| SEWS ONE-THIRD FASTER |
| Than Any Vibrating Shuttle Machine. |
| For Family and Manufacturing Purposes |
| Wheeler & Wilson Mfg. Co., |
| 82 & 80 WABASH AVE., |
- 149 -

- 150 -
| 82 MADISON ST., |
| Rooms 5, 6 and 7, |
| McVicker's Theatre Building. |
| Dutton & Peterson |
| TAILORS. |
| Fine |
| Tailoring |
| AT |
| Moderate |
| Prices. |
- 151 -
| L. A. Melze, M.D., D.D.S., & Sons | ||
| PAINLESS AND | ||
| HIGH-CLASS | ||
| DENTISTRY. | ||
 | ||
| Bridge and Crown Work a Speciality. | ||
| ||
| ||
| Hours 8 a.m. to 9 p.m. Sundays 9 a.m. to 4 p.m. | ||
| Ladies in attendance. Phone 1596 Main. | ||
| L. A. HELZE, M.D., D.D.S., & SONS | ||
| .....SUPERIOR DENTAL PARLORS..... | ||
|
- 152 -
Goldman's Automatic Binder.
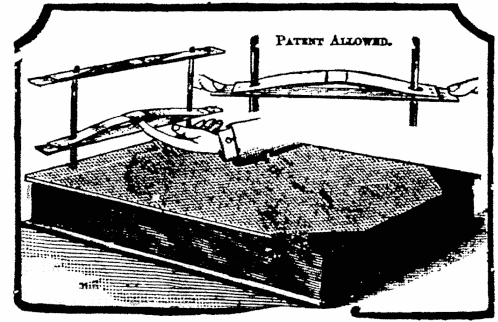 | ||||||||||||||||
Is a convenient device for permanently filing and binding Papers,
Bills, Orders, etc. It is self-locking and self-opening, the simple
effort of removing the cover releasing the same automatically. It can
be permanently locked and unlocked, offers no protruding points,
and is easily operated with two fingers of one hand. No screws to
wind or unwind. No keys to get lost or mislaid. No rough surfaces
to scratch the desk. Locking device can be attached to cover and
readily separated.
| ||||||||||||||||
| ||||||||||||||||
| Smith's Interest Tables |
| Are the simplest and most convenient ever published, and are ab- solutely correct, having stood the test for years. The book shows the interest on any sum from $1 to $10,000. at any rate from one day to five years. It also contains compound interest tables, time tables, and tables for 33, 63 and 93 days. |
| Sent, bound in cloth, postpaid, on receipt of $1. |
| The Smith-Tickler Co. |
| _________RACINE, WIS. |
Mention Arithmachinist when placing Orders or making Inquiries.
- 153 -
 STRONGEST
PREVENTIVE OF FORGERIES!
STRONGEST
PREVENTIVE OF FORGERIES! | ||||||
| Unequaled Advantages! | ||||||
| ||||||
| COMPLETE SECURITY OUTFIT, $2.00. | ||||||
| Style of firm incorporated without extra charge. Instructive pamphlet, giving valuable hints regarding check-raising and its prevention, 10c. Sent postpaid, on receipt of price, by | ||||||
| ||||||
- 154 -
THE LATEST
IN
Order Blank and Receipt Holders
MADE ENTIRELY OF ALUMINUM.

| |
| |
| CHICAGO SHIPPING & RECEIPT BOOK CO. | |
| SOLE MANUFACTURERS, | |
| 195-199 S. Clark Street, - - CHICAGO, ILL. |
- 155 -
| Established 1862 | Phone Main 68, |
| H. H. HOFFMANN & CO., | |
| HEADQUARTERS FOR THE PEERLESS CONTINOUS | |
| LOOSE LEAF LEDGER | |
| AND BLANK BOOK MAKERS, | |
| 175 Monroe Street, - | - Chicago, lllinois. |
 Patented September 22nd, 1896.
"THE PERFECT BOOK,"
When locked it will be impossible to remove a leaf.
When unlocked, leaves can be extracted and replaced
instantly at any point.
The Book-Keeper's Time Saver and Systemizer.
Best arrangement for keeping accounts in the latest
approved a most orderly system.
The Loose Leaf Ledger System has come to stay.
It is in the lead with up-to-date book-keepers.
Patented September 22nd, 1896.
"THE PERFECT BOOK,"
When locked it will be impossible to remove a leaf.
When unlocked, leaves can be extracted and replaced
instantly at any point.
The Book-Keeper's Time Saver and Systemizer.
Best arrangement for keeping accounts in the latest
approved a most orderly system.
The Loose Leaf Ledger System has come to stay.
It is in the lead with up-to-date book-keepers.
 LEDGER EXPANDED.
Showing how leaves are placed and securely held by two Posts and
End Boxes. There is nothing better for the purpose.
Durability, Security, Simplicity and Reasonable Prices our Motto.
LEDGER EXPANDED.
Showing how leaves are placed and securely held by two Posts and
End Boxes. There is nothing better for the purpose.
Durability, Security, Simplicity and Reasonable Prices our Motto. | |
- 156 -
| THE BAIRD CHRONOGRAPH. ————— THE ONLY RELIABLE TIME STAMP. ————— | ||||
| ||||
 | ||||
| ||||
| WRITE FOR PARTICULARS. Baird Clock Co., | ||||
| ||||
- 157 -
 | ||||
| Size, 4½ x 1½ x ¾ in. Weight, less than 1 lb. | ||||
| SMALLEST, LIGHTEST, CHEAPEST, SIMPLEST, STRONGEST, FASTEST, | ||||
| PRACTICAL Computing Machine, | ||||
| Which adds, subtracts, multiplies, divides, etc., whole num- bers, decimal and common fractions, as well as denominate quantities, and carries any number of columns simultaneously | ||||
| ||||
| No Noise! No Jar! No Strain. Built of Metal, Highly Finished. | ||||
| ||||
| ||||
| The Office Men's Record Co., | ||||
| ||||
- 158 -
| GUARANTEE Accompanying Every Arithmachine. —————— | |
| CHICAGO, | |
| |
| The Office Men's Record Co., | |
| HENRY GOLDMAN, Treas. |
- 159 -
| ORDER BLANK. | ||
| ||
| ||
| Gentlemen:- Please enter order for GOLDMAN'S ARITHMACHINE , Capacity, Col., Price, $ for which enclose the above named amount in current funds. | ||
| Express charges prepaid to any address, if remittance accompanies the order. Goldman's "Arithmachinist," a complete self-instructor in Mechanical Arithmetical, price, separately, $1.00. sent Free with each Arithmachine. Bound in Cloth, 25 cts. additional. Bound in Leather, 50 cts. additional. |
- 160 -
| REBATE COUPON | |||||||||||||||
| |||||||||||||||
| Chicago, | |||||||||||||||
| GOOD FOR ONE DOLLAR | |||||||||||||||
| |||||||||||||||
| THE OFFICE MEN'S RECORD CO., | |||||||||||||||
| HENRY GOLDMAN, Treas. | |||||||||||||||
| . . . PRICE LIST . . . | |||||||||||||||
| |||||||||||||||
| |||||||||||||||
| Stylus Pencils, per Doz., 50 cts.; Erasable Tablets, per Doz., 10 cts | |||||||||||||||
| When using this Rebate Coupon fill out Order Blank on opposite side, and detach at perforated line. |
- 161 -

 without touching
the coin or tearing
the paper.
without touching
the coin or tearing
the paper.