Jaap's Puzzle Page

Butterfly

Butterfly

The Butterfly puzzle is a beautiful wooden puzzle by Clever Toys that has two loops of balls side by side. In the middle is a sliding part that contains a section of track that is shared by the to loops. If the slide is to the left, only the balls in the left loop can be moved, as the right loop is incomplete. Similarly only the right loop can move if the slide is on the right. The seem to be 18 balls in a complete loop, of which four lie on the section on the slide. However, a loop actually has a single ball, followed by a pair of balls stuck together, then another single ball, another connected pair, and so on all the way around the loop. The five balls (pair, single, pair) in top section of each loop are coloured yellow, and the five balls at the bottom (again a pair, single, pair) are coloured brown. The aim of the puzzle is of course to recover this colour pattern after it has been mixed.

This puzzle was invented and patented by Martin Lapeš, CZ 13357, published 9 June 2003.

If your browser supports it, you can click on the link below to play with a Javascript version of the Butterfly puzzle.

Javascript Butterfly

The number of positions:

The alternating arrangement of pairs and single balls will always remain alternating when it is mixed. There are 10 single balls and 11 pairs, so there are at most 11!·10! positions. This limit is not reached because there are many sets of identical pieces. There are 2 brown, 2 yellow and 6 blank single balls, and 4 brown, 4 yellow, 3 blank ball pairs. This leaves 10!·11! / (2!2·6!·4!2·3!) = 14,553,000 positions.

I have done a computer analysis of the Butterfly puzzle in order to find God's Algorithm for it. The results are in the table below. Analogous to the Rubik's cube, there are two ways to count the moves. The Face Turn Metric means that a shifting the balls of either loop by any amount is a single move. The "Quarter" Turn Metric means that only shifting a loop by 3 balls is counted as a single move. The tables show that it can be solved in no more than 13 face turns (10.334 on average), or at most 20 three-ball shifts (15.780 on average).

Face turn metric
012345678910111213Total
Q
u
a
r
t
e
r

t
u
r
n

m
e
t
r
i
c		011
144
24812
32161634
416482892
587212052252
616424828898699
7323207586561681,934
882641,2462,0941,4402725,324
91401,3984,2665,4482,99236814,612
10441,0726,04813,20013,6585,19041039,622
1185806,12822,73039,39229,5986,636232105,304
121924,33028,05680,496105,52447,7384,60428270,968
13322,02425,260120,366260,976212,37441,018758662,808
14458015,678128,140457,610645,133223,0238,796201,478,984
15966,08289,532545,1201,322,250807,75057,142682,828,040
161,10035,292378,9791,626,2401,824,024234,8105484,100,993
17805,834121,010934,3932,026,794519,4642,1383,609,713
1822411,560167,624732,414404,7154,7711,321,308
191404,83045,53158,6982,203111,402
20420461868894
Total110492401,1725,62226,320119,242516,1981,916,0754,967,6325,705,5941,285,0299,81614,553,000

Three of the 68 most difficult positions are shown below. Their mirror images form three more.

Butterfly hardest positions

Solution:

This puzzle is very closely related to the Turnstile and Puzzler. In fact there is a direct correspondence between their pieces: The single balls are equivalent to the triangular 'corners', and the ball pairs are equivalent to the rectangular 'edges'. If you understand how to solve Turnstile, then this correspondence makes it quite easy to solve the Butterfly, too.

Notation:

Let a clockwise shift of the left loop by three balls be denoted by L. An anti-clockwise shift of the left loop by three balls is denoted by L'. Turns of the right loop are denoted in the same way, but using the letter R instead, so R for a clockwise and R' for an anti-clockwise shift of the right loop by three balls.

A solution for the Butterfly puzzle is fairly easily constructed by the use of the simple move sequence LR'L'R. This sequence swaps two pairs of single balls, and also does a 3-cycle of ball pairs. If you perform it twice then the single balls remain unmoved but it is still a 3-cycle of ball pairs. If you perform it three times then the ball pairs remain unmoved but still does a double swap of single balls, though if you solve the single balls before solving the ball pairs you don't need to do this. Below I will explain a solution to the Butterfly puzzle in more detail.

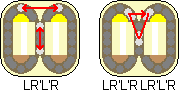
Move sequences

Solution:

Phase 1: Solve the single balls.
Hold the puzzle with the yellow end at the top, and the brown end at the bottom.
  1. Bring one of the single yellow balls to the left loop (not on the slide), and one of the brown balls to the right loop (again not on the slide). This is quit easy.
  2. Turn the left loop so that the yellow ball lies on the left hand side of the loop, just above the middle.
  3. Turn the right loop so the brown ball lies at the bottom end of the slide.
  4. Turn the left loop so that the yellow and brown balls are at their correct spots at the top and bottom of the loop.
  5. Turn the right loop so that the other yellow or other brown ball lies at the bottom end of the slide, and the top end of the slide has a blank ball.
  6. Do LLL, i.e. shift the left loop by 9 balls (exchanging the top/bottom balls, bringing the coloured ball the left, above centre).
  7. Turn the right loop so that the other remaining coloured ball lies at the right, just above the middle.
  8. Do LLL again, i.e. shift the left loop by 9 balls (restoring the top/bottom balls again).
  9. Turn the right loop so that its two coloured balls are in their correct spots at the top and bottom of the loop.

Phase 2: Solve the ball pairs.

  1. If there is a coloured ball pair on the slide, then go to step d.
  2. If there is a coloured ball pair on the left of the left loop, then do LLL RRR LLL RRR. This brings the coloured pair to the slide. Then go to step d.
  3. If there is a coloured ball pair on the right of the right loop, then do RRR LLL RRR LLL. This brings the coloured pair to the slide. Then go to step d.
  4. To place the centre ball pair in position, then do one of the following sequences depending on where it should go:
    Top left of left loop: RL LR'L'R LR'L'R L'R'
    Top right of left loop: R'LRL' R'LRL'
    Top left of right loop: LR'L'R LR'L'R
    Top right of right loop: L'R' R'LRL' R'LRL' RL
    Bottom left of left loop: R'L' L'RLR' L'RLR' LR
    Bottom right of left loop: RL'R'L RL'R'L
    Bottom left of right loop: L'RLR' L'RLR'
    Bottom right of right loop: LR RL'R'L RL'R'L R'L'
    Note that if you could not get a coloured ball pair to the centre in steps a-c, then by the same method you can use the blank centre pair to displace any incorrectly placed ball pair.
  5. Repeat steps a-d until the puzzle is solved.

Pretty Patterns for Butterfly:

1. R'LL RRL R'LL R'LL RL' RL'L' R'L'
2. L'RR LLLR' LLRRR LRRL