







The Turnstile puzzle consists of two overlapping circular disks. Each disk has 12 pieces, 6 are triangular ('corners'), 6 rectangular ('edges') alternating along the rim of the disk around a hexagonal centre. The pieces have curved sides. The disks have three pieces in common, two corners and one edge, so there are altogether 10 corners and 11 edges. Each disk can be rotated. A rotation should be a multiple of 60 degrees since only then can the other disk move again.
There are 5 bright colours used for the corners, a pair of each colour. There is one edge of each of those colours, and the remaining 6 edges are grey. The aim is to put together all pieces of the each colour. The only way to do this is by forming coloured 'lozenges' of two adjacent corners and the edge between them. These lozenges are separated from each other by the grey edges. The rim of the puzzle has small coloured markings, so that the colours of the lozenges should be such that they match the markings.
Turnstile was manufactured by Binary Arts (now called ThinkFun). There is also a version called TwinSpin that was made in the far East. Turnstile was licensed however from Douglas A. Engel who originally invented and produced it. He patented it on 15 November 1983, US4,415,158. He first called it Engel's Enigma, but later marketed it as The Puzzler with three different designs of varying difficulty:

Note that the Puzzlers sold in the USA were manufactured there and have a hexagonal white base, whereas those sold in the rest of the world were made in Taiwan and have a black oval base.
These puzzles were invented by Douglas A. Engel, who also invented various other puzzles such as:
If your browser supports it, you can click on the link below to play with a Javascript version of the Turnstile puzzle or any Puzzler variation.
A related puzzle is made in Russia, and called Trio. It has three intersecting disks, arranged in a triangle. The pieces are inside a casing transparent on both sides, and has a slightly different colour scheme on each side. The pieces in the overlapping areas are yellow, the rest of the three disks are red, green, and blue. The other side is the same except that six edges adjacent to the yellow centre are coloured white.
There are 10 corners and 11 edges, so there are at most 11!·10! positions. This limit is not reached on any of these variations because there are many sets of identical pieces. The following table shows the numbers for each variation.
| Corners | Edges | Positions | ||
|---|---|---|---|---|
| Puzzler Novice | 4, 6 | 5, 6 | 10!·11! / (4!·5!·6!2) | 97,020 |
| Puzzler Challenger | 5, 5 | 3, 4, 4 | 10!·11! / (3!·4!2·5!2) | 2,910,600 |
| Puzzler Avenger / Turnstile | 2, 2, 2, 2, 2 | 1, 1, 1, 1, 1, 6 | 10!·11! / (2!5·6!) | 6,286,896,000 |
Remember however that the Puzzler avenger actually has 5!=120 solutions due to the lack of markings. Equivalently you can consider the positions that differ by a permutation of colours to be the same, and then it has one solution but only 10!·11! / (2!5·6!·5!)=52,390,800 positions.
I have done a computer analysis of the Puzzler Novice, Puzzler Challenger, and Puzzler Avenger in order to find God's Algorithm for them. The results are in the tables below. Analogous to the Rubik's cube, there are two ways to count the moves. The Face Turn Metric means that a turn of either disk by any amount is a single move. The Sixth Turn Metric means that only 60 degree turns are single moves.
Puzzler Novice:
| Face turn metric | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | Total | ||
| S i x t h t u r n m e t r i c | 0 | 1 | 1 | |||||||||||||
| 1 | 2 | 2 | ||||||||||||||
| 2 | 2 | 4 | 6 | |||||||||||||
| 3 | 1 | 8 | 8 | 17 | ||||||||||||
| 4 | 8 | 24 | 14 | 46 | ||||||||||||
| 5 | 4 | 34 | 50 | 24 | 112 | |||||||||||
| 6 | 1 | 25 | 98 | 116 | 32 | 272 | ||||||||||
| 7 | 7 | 121 | 294 | 200 | 34 | 656 | ||||||||||
| 8 | 85 | 424 | 687 | 296 | 18 | 1,510 | ||||||||||
| 9 | 35 | 397 | 1,327 | 1,265 | 262 | 16 | 3,302 | |||||||||
| 10 | 6 | 225 | 1,539 | 3,048 | 1,546 | 225 | 11 | 6,600 | ||||||||
| 11 | 68 | 1,115 | 4,381 | 5,051 | 1,391 | 98 | 2 | 12,106 | ||||||||
| 12 | 7 | 432 | 3,681 | 9,064 | 5,193 | 557 | 12 | 18,946 | ||||||||
| 13 | 56 | 1,510 | 8,701 | 10,398 | 2,260 | 72 | 22,997 | |||||||||
| 14 | 3 | 194 | 3,393 | 9,719 | 4,864 | 372 | 18,545 | |||||||||
| 15 | 10 | 299 | 3,101 | 4,532 | 947 | 16 | 8,905 | |||||||||
| 16 | 7 | 192 | 1,376 | 921 | 84 | 6 | 2,586 | |||||||||
| 17 | 1 | 62 | 209 | 97 | 12 | 381 | ||||||||||
| 18 | 11 | 16 | 3 | 30 | ||||||||||||
| Total | 1 | 5 | 25 | 98 | 409 | 1,555 | 5,391 | 14,419 | 28,341 | 30,236 | 13,760 | 2,546 | 213 | 21 | 97,020 | |
The three most difficult positions are shown here:

Puzzler Challenger:
| Face turn metric | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | Total | ||
| S i x t h t u r n m e t r i c | 0 | 1 | 1 | |||||||||||||
| 1 | 4 | 4 | ||||||||||||||
| 2 | 4 | 8 | 12 | |||||||||||||
| 3 | 2 | 16 | 12 | 30 | ||||||||||||
| 4 | 16 | 36 | 24 | 76 | ||||||||||||
| 5 | 8 | 56 | 96 | 48 | 208 | |||||||||||
| 6 | 2 | 52 | 200 | 232 | 82 | 568 | ||||||||||
| 7 | 32 | 252 | 612 | 516 | 148 | 1,560 | ||||||||||
| 8 | 12 | 228 | 980 | 1638 | 1132 | 232 | 4,222 | |||||||||
| 9 | 2 | 140 | 1130 | 3334 | 4350 | 2044 | 200 | 11,200 | ||||||||
| 10 | 56 | 904 | 4922 | 10475 | 9882 | 2688 | 78 | 29,005 | ||||||||
| 11 | 12 | 500 | 5198 | 18460 | 29879 | 16130 | 1628 | 16 | 71,823 | |||||||
| 12 | 2 | 220 | 3658 | 22980 | 62220 | 61987 | 13273 | 368 | 4 | 164,712 | ||||||
| 13 | 54 | 1530 | 19084 | 88973 | 155887 | 65166 | 4096 | 48 | 334,838 | |||||||
| 14 | 309 | 9514 | 80520 | 250552 | 204084 | 25234 | 548 | 570,761 | ||||||||
| 15 | 24 | 2298 | 39498 | 232216 | 376516 | 95187 | 2918 | 8 | 748,665 | |||||||
| 16 | 176 | 8176 | 99035 | 340627 | 189255 | 10502 | 14 | 647,785 | ||||||||
| 17 | 448 | 13915 | 107117 | 144389 | 18108 | 30 | 284,007 | |||||||||
| 18 | 4 | 372 | 6752 | 25210 | 8100 | 28 | 40,466 | |||||||||
| 19 | 24 | 338 | 293 | 2 | 657 | |||||||||||
| Total | 1 | 10 | 50 | 202 | 1,010 | 4,680 | 21,211 | 88,617 | 321,876 | 832,982 | 1,115,265 | 484,093 | 40,521 | 82 | 2,910,600 | |
The two most difficult positions are shown here:
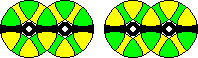
Puzzler Avenger:
Note that positions that differ by swapping around the colours are considered the same,
so it can be solved with the colours in any order.
| Face turn metric | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | Total | ||
| S i x t h t u r n m e t r i c | 0 | 1 | 1 | |||||||||||||||
| 1 | 2 | 2 | ||||||||||||||||
| 2 | 4 | 4 | ||||||||||||||||
| 3 | 4 | 8 | 12 | |||||||||||||||
| 4 | 2 | 16 | 16 | 34 | ||||||||||||||
| 5 | 16 | 52 | 24 | 92 | ||||||||||||||
| 6 | 8 | 68 | 128 | 48 | 252 | |||||||||||||
| 7 | 2 | 58 | 252 | 304 | 96 | 712 | ||||||||||||
| 8 | 30 | 296 | 792 | 668 | 176 | 1,962 | ||||||||||||
| 9 | 8 | 236 | 1,210 | 2,174 | 1,466 | 304 | 5,398 | |||||||||||
| 10 | 2 | 125 | 1,244 | 4,216 | 5,638 | 3,054 | 482 | 14,761 | ||||||||||
| 11 | 46 | 934 | 5,642 | 13,172 | 14,200 | 5,798 | 662 | 40,454 | ||||||||||
| 12 | 12 | 556 | 5,374 | 21,714 | 39,337 | 32,672 | 9,570 | 540 | 109,775 | |||||||||
| 13 | 2 | 240 | 3,942 | 25,888 | 77,348 | 108,626 | 66,088 | 10,758 | 168 | 293,060 | ||||||||
| 14 | 64 | 2,232 | 23,298 | 111,782 | 258,262 | 270,459 | 92,648 | 5,190 | 4 | 763,939 | ||||||||
| 15 | 8 | 944 | 16,078 | 122,424 | 452,700 | 779,472 | 476,602 | 59,118 | 466 | 1,907,812 | ||||||||
| 16 | 1 | 226 | 8,405 | 100,270 | 580,475 | 1,630,022 | 1,694,946 | 385,142 | 6,112 | 4,405,599 | ||||||||
| 17 | 32 | 3,032 | 58,622 | 526,306 | 2,380,099 | 4,225,878 | 1,666,086 | 46,502 | 8,906,557 | |||||||||
| 18 | 574 | 21,260 | 305,970 | 2,213,807 | 6,766,089 | 4,732,559 | 227,279 | 4 | 14,267,542 | |||||||||
| 19 | 34 | 3,728 | 95,140 | 1,082,128 | 5,640,167 | 7,221,425 | 641,574 | 64 | 14,684,260 | |||||||||
| 20 | 248 | 10,712 | 192,953 | 1,638,739 | 3,871,877 | 695,213 | 174 | 6,409,916 | ||||||||||
| 21 | 240 | 6,398 | 82,914 | 353,130 | 133,180 | 58 | 575,920 | |||||||||||
| 22 | 4 | 208 | 1,412 | 1,108 | 4 | 2,736 | ||||||||||||
| Total | 1 | 2 | 10 | 50 | 234 | 1,121 | 5,401 | 25,546 | 119,475 | 552,577 | 2,377,383 | 8,631,662 | 20,629,489 | 18,296,107 | 1,751,438 | 304 | 52,390,800 | |
The four most difficult positions are shown here, but remember that the colours are arbitrary:

Turnstile:
The following tables were calculated by Tom Rokicki.
| Face turn metric | Sixth turn metric | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
The table below summarizes the depth of the worst cases (i.e. diameters) and average depths for both metrics.
| Face Turn Metric | Sixth Turn Metric | |||
|---|---|---|---|---|
| Worst | Average | Worst | Average | |
| Puzzler Novice | 13 | 8.3522 | 18 | 12.533 |
| Puzzler Challenger | 13 | 9.5556 | 19 | 14.675 |
| Puzzler Avenger | 15 | 12.117 | 22 | 18.003 |
| Turnstile | 17 | 14.027 | 26 | 21.460 |
Let a clockwise 60 degree rotation of the left disk be denoted by L. Rotations of 120, 180, 240, 300 degrees are then denoted by L2, L3, L4 and L5. Note that L5 can also be considered an anti-clockwise 60 degree turn, and is therefore also denoted by L'. Turns of the right disk are denoted in the same way, but using the letter R.
A solution for any variation of the puzzle is fairly easily constructed by the use of the simple move sequence LR'L'R. This sequence swaps two pairs of corners, and also does a 3-cycle of edges. If you perform it twice then the corners remain unmoved but it is still a 3-cycle of edges. If you perform it three times then the edges remain unmoved but still does a double swap of corners, though if you solve the corners before solving the edges you don't need to do this. Below I will explain a solution to the standard Turnstile and Avenger puzzles which uses some shortcuts instead of applying this move sequence all the time.
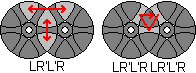
Phase 1: Pair up the corners.
Phase 2: Place the edges correct.
Phase 3: Place the lozenges correct.
| 1. | L R L R L R L R3 L R' L' R' |  |
|---|---|---|
| 2. | L R' L R' L R' L R' L R' |  |
| 3. | L R L2 R' L' R L' R' L R' L R4 |  |
| 4. | L4 R' L R L3 R L' R L' R L' R L2 R L' |  |
| 5. | R L R4 L R L' R2 L | 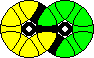 |