Jaap's Puzzle Page

Palette 7

Palette 7

Palette 7 is a puzzle with 7 square numbered pieces. The pieces lie inside a 3×3 base, and are also held inside a cross-shaped frame. The top and bottom arms of this cross can hold only 1 piece, and the left and right arms a 2×2 square of pieces. By moving the frame horizontally or vertically, the pieces are moved about the 3×3 square. In the solved position the frame is at the bottom right, with piece 1 on its own in the top row, and below that rows containing 2,3,4 and 5,6, and 7.

These puzzles were invented by Douglas A. Engel, who also invented various other puzzles such as:

If your browser supports JavaScript, then you can play Palette 7 by clicking the link below:

JavaScript Palette 7

The number of positions:

There are 7 pieces and, as with any puzzle that essentially only uses plungers to move the pieces, only even permutations of the pieces are possible. This gives 7! / 2 = 2520 positions of the pieces for any frame position. The frame can be positioned in 3×2 = 6 ways, so there are really only 6·7! / 2 = 15,120 positions.

I used a computer to calculate God's algorithm, and the result is shown in the following table. Sliding the frame one tile in any direction is considered a single move. Every position can be solved in at most 37 moves (25.469 on average).

Moves   Positions
01
12
23
35
46
57
611
716
819
925
1037
1147
1256
Moves   Positions
1379
14110
15133
16165
17227
18299
19369
20477
21630
22771
23921
241078
251210
Moves   Positions
261320
271366
281369
291351
301194
31873
32519
33263
34117
3535
368
371
Total15120

Antipode The unique antipodal position at depth 37 is shown on the left.


Links to other useful pages:


PuzzleAtomic.com is the homepage of Douglas Engel, the inventor and manufacturer.

Notation:

Sliding the frame left or right by exactly one tile is denoted by L or R respectively. In the same way moving it up or down is denoted by U or D.

Solution:

There are two move sequences that we will use in the solution. Start with frame at the bottom-centre position, so that single piece in the top row is centred. The two move sequences we can do are then:

LURDAnti-clockwise 5-cycle of left hand side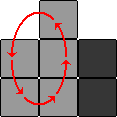
RULDClockwise 5-cycle of right hand side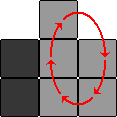

Of course these sequences can also be done in reverse to cycle pieces in the opposite direction.
These move sequences can be combined to make one much more useful one:

(RULD LURD LURD)23-cycle of right hand column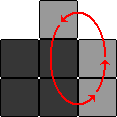

This sequence consists of the previously mentioned right and left cycles, in the order right, left, left, right, left, left.

  1. Move the frame to the bottom-centre position, so that single piece in the top row is centred.
  2. Find piece number 5. If it lies in the right hand side column, then cycle the right side to bring it to the middle column.
  3. Cycle the left side until piece number 5 is in position at the bottom left.
  4. If piece 2 is not in position directly above piece 5, then
    1. cycle the right side to bring piece 2 to the top or centre of the middle column.
    2. cycle the left clockwise once (ULDR), moving piece 5 upwards.
    3. cycle the right side to bring piece 2 to the top of the middle column.
    4. cycle the left anti-clockwise once (LURD), moving pieces 2 and 5 downwards into position.
  5. Cycle the right side to bring piece 6 to the bottom of the middle column.
  6. If piece 3 is to the right of piece 6, at the bottom-right corner, then apply the 3-cycle to move it away from there.
  7. Put piece 3 in position as follows:
    1. Cycle the right clockwise once (RULD), moving piece 6 upwards, with the 3 somewhere in the right column.
    2. Apply the 3-cycle once or twice to bring piece 3 to the top of the middle column.
    3. Cycle the right anti-clockwise once (URDL), and 3 and 6 should now be correct.
  8. Apply the 3-cycle once or twice to bring piece 1 to the top. Pieces 4 and 7 should then automatically be correct as well.