Palette 21

Palette 21 is a wooden puzzle with 21 square pieces. The pieces lie inside a 5×5 base, and are also held inside a cross-shaped frame. The arms of this cross are three pieces wide and 2 pieces long. By moving the frame horizontally or vertically, the pieces are moved about the 5×5 square. In the solved position the frame is at the bottom right, the top arm of the cross has six green pieces, the left arm has six blue pieces, and the centre has the nine red pieces.

This puzzle were invented by Douglas A. Engel, who also invented various other puzzles such as:

Matt Galla was first to calculate God's algorithm for this puzzle, and I have been able to replicate his results. If a move is defined as sliding the frame exactly one step in any direction, then every position can be solved in at most 50 moves (or 40.060 on average). If a move is a shift of the frame by any distance in any one direction, then it takes at most 38 moves (average 30.654).

Sliding frame exactly one tile is one move

Sliding frame in one direction is one move

Depth	# positions
0	1
1	2
2	4
3	8
4	16
5	20
6	40
7	68
8	132
9	164
10	297
11	416
12	778
13	1,068
14	2,034
15	2,902
16	5,548

Depth	# positions
17	7,758
18	14,723
19	20,490
20	38,665
21	53,680
22	101,340
23	140,664
24	264,553
25	363,856
26	679,674
27	926,190
28	1,715,255
29	2,305,824
30	4,220,638
31	5,574,508
32	10,037,660
33	12,923,632

Depth	# positions
34	22,744,263
35	28,247,070
36	48,050,536
37	56,443,214
38	91,008,329
39	97,557,952
40	143,360,318
41	129,664,672
42	159,303,960
43	102,195,262
44	87,917,360
45	28,144,016
46	12,390,136
47	1,011,138
48	125,136
49	546
50	4
Total	1,047,566,520

Depth	# positions
0	1
1	4
2	8
3	16
4	32
5	64
6	128
7	250
8	442
9	841
10	1599
11	3042
12	5790
13	11065
14	21073
15	39898
16	75232
17	141851
18	266471
19	497446

Depth	# positions
20	922511
21	1695721
22	3086242
23	5534932
24	9755387
25	16821968
26	28242168
27	45839411
28	71301348
29	104976901
30	143627046
31	177043276
32	186192809
33	151142652
34	79126738
35	19733802
36	1444614
37	13736
38	5
Total	1,047,566,520

The four antipodes for the single step moves are:

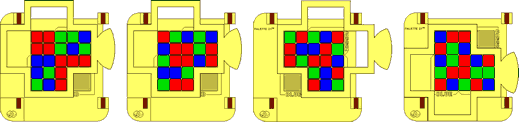
Palette 21 - the 4 antipodes, single step moves

The five antipodes for the single direction moves are:

Palette 21 - the 5 antipodes, single direction moves

Notation:

Sliding the frame left or right by exactly one tile is denoted by L or R respectively. In the same way moving it up or down is denoted by U or D.
The rows of the 5×5 square are denoted by the letters A to E from top to bottom, and the columns 1 to 5 from left to right. Any piece location can then be specified by a letter/number combination.

Solution:

Phase 1: Solve the top three green pieces.

Move the frame to the bottom-centre position, i.e. centred on location D3.
If there is a green piece at one of the positions B2, B3, B4, C5, D5, E5, E4, E3, E2, D2, C2, then do the move sequence URDL (or its inverse RULD), and repeat that move sequence until the green piece lies at B4. Then go to step d.
If, on the other hand, there is a green piece at one of the positions C4, D4, C1, D1, E1, then do the move sequence ULDR (or its inverse LURD), and repeat that move sequence until the green piece lies at B4.
Move the green piece from B4 to the top row by doing the move sequence ULURDD.
Repeat steps b-d two more times, until the top row is green.

Phase 2: Put the next three green pieces in column 5.
Note that the remaining green pieces will be placed in column 5, and only put into place in row 2 at the end of the next phase.

Make sure the frame is once again at the bottom-centre position, i.e. centred on location D3.
If D3 is green, then do the following steps to make it non-green:
1. Use repetitions of ULDR or URDL to bring a green tile to B2.
2. If E5 is green, then repeat RULD LURD as often as needed until E5 is no longer green.
3. Do U RULD D. This replaces one of the greens in row A, and displaces D3 in the process.
Repeat the move sequence URDL (or its inverse RULD) as often as necessary to make locations C2 and D2 not green. If you can make C5 green at the same time, then do so.
Repeat move sequence ULDR (or its inverse LURD), until B4 is green, and E2 is not green.
Do RULD, which will insert the green piece into column 5.
Repeat steps d-e until all three remaining green pieces are in column 5.

Phase 3: Solve the blue pieces, and put the greens in place.
Note that in this phase we will build up a string of blue pieces that starts at B4. Eventually we will have the blue pieces at B4, C4, D4, E4, E3, E2, and from there is is easy to solve.

Make sure the frame is once again at the bottom-centre position, i.e. centred on location D3.
Repeatedly do ULDR until you have a position with C1 and D1 red. On very rare occasions this is not possible, and then just make sure that D1 is red. You often have a choice of red(s), so to speed things up do this in such that you have as long a string of blue pieces as possible at B4 downwards.
Do LURD three times to return the green pieces to the top.
If D2-3 and E1-4 are all red, do RULURDLD once or twice until this is no longer the case.
Do ULURDLDR (or its inverse LURULDRD) as often as neccesary to make D2 blue and E1 red.
Do RULD three times, putting the green pieces of row B into column 5.
Do ULDR, which makes the string of blues one longer than it was before.
If the six blue pieces are not yet all in one string at B4, C4, D4, E4, E3, E2, then go back to step c.
Do LURD six times, so that the blue pieces now fill column A and row B.
Do URDL three times, which moves the blue pieces from row B to column 2, and the greens from column 5 to row B.
Do R, to put the frame in the correct position.

Jaap's Puzzle Page

Palette 21

Javascript Palette 21

The number of positions:

Links to other useful pages:

Notation:

Solution: