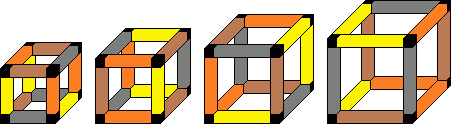Instant Indecision is a puzzle made in 1972 by The Green Gate Company. It consists of a pedestal and
four wire-frame cubes of different sizes which, when placed on the pedestal, fit concentrically
inside each other. The edges of the cubes come in four colours. The aim is to arrange the cubes such
that each row of four corresponding edges of the cubes show all four colours.
The puzzle is clearly inspired by Instant Insanity.
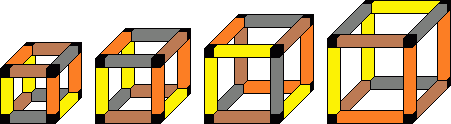
Each cube has 24 orientations, giving a maximum of 244 positions. Whichever way the first cube is placed, the solution you are aiming for can be rotated to match, so it doesn't really matter how the first cube is placed. This essentially leaves only 243 = 13,824 positions.
The puzzle can be solved fairly easily by trial and error, but there is a way to reduce the search space considerably.
A cube has four main diagonals. The 24 ways of orienting a cube correspond exactly to the 4! ways of permuting those four diagonals. We can split the 12 edges of a cube into four sets of three edges which are symmetrically arranged around the diagonals.
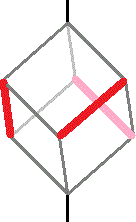
Using Y=Yellow, O=Orange, B=Brown, L=Black, we have the following sets:
| Cube | Sets (in no particular order) | |||
|---|---|---|---|---|
| 1 (small) | YYB | YLL | OOL | OBB |
| 2 | YYL | YBB | OOB | OLL |
| 3 | YYB | YOB | OOB | LLL |
| 4 (large) | YLL | YOB | YBB | OOL |
When the puzzle is assembled, each diagonal has a set of edges from each cube, which combined should form three rows, and so they should contain 3 edges of each colour. So we should rearrange the order of each row in the above table so that each column has three of each letter. The set of three black edges on the third cube is the most restrictive - the only sets it can be combined with have brown, so to get exactly three brown edges there must be one in each set, which leaves only one way to form this column:
| Cube | First diagonal solved, rest in no particular order | |||
|---|---|---|---|---|
| 1 (small) | YYB | YLL | OOL | OBB |
| 2 | OOB | YYL | YBB | OLL |
| 3 | LLL | YYB | YOB | OOB |
| 4 (large) | YOB | YLL | YBB | OOL |
There is only way to get three orange edges in the column headed by YLL, which gives:
| Cube | First two diagonals solved, rest in no particular order | |||
|---|---|---|---|---|
| 1 (small) | YYB | YLL | OOL | OBB |
| 2 | OOB | YBB | YYL | OLL |
| 3 | LLL | YOB | YYB | OOB |
| 4 (large) | YOB | OOL | YLL | YBB |
The last two columns are then easy:
| Cube | Solved | |||
|---|---|---|---|---|
| 1 (small) | YYB | YLL | OOL | OBB |
| 2 | OOB | YBB | OLL | YYL |
| 3 | LLL | YOB | YYB | OOB |
| 4 (large) | YOB | OOL | YBB | YLL |
This corresponds to the following solution: