Jaap's Puzzle Page

"It" / 4x4 / Tsukuda's Square

It Tsukuda's Square

Tsukuda's Square, also known as 4x4 or "It", is a very difficult type of sliding piece puzzle. It consists of 16 tiles in a 4x4 square. On the left of each row is a plunger, which pushes that row one tile to the right. At the top is a large plunger which pushes the three rightmost columns down one tile. Springs push back the plungers as soon as they are released. If the top plunger is pushed in, the first row plunger can no longer move.

There are several different designs (see also Cubic Circular Issue 2 p9). The version that was marketed in Britain was called "It", and it had tiles that were numbered 1 to 16, and the tiles were also made of four different colours plastic, four each of the colours green, red, yellow, and blue. In the USA the puzzle was marketed by Gabriel under the name "Tsukuda's Square", and it apparently came in several different versions. The most difficult version has black tiles numbered from 1 to 16. A version in which the tiles are split diagonally half-red and half-white is shown above as well. There are 4 sets of 4 identical tiles in that version. That design was also done in blue and white. I believe the third version simply has four tiles of four colours.

Tsukuda's Square is closely related to Rubik's Fifteen, but much more difficult because it has fewer plungers. It was invented by Toshihisa Suga, patented on 26 January 1983, GB 2,101,897.

If your browser supports JavaScript, then you can play the 'It' puzzle by clicking the link below:

JavaScript 'It' puzzle

The number of positions:

There are 16 pieces, and hence a maximum of 16! positions (where the plungers are not pushed in). This limit is not reached since only even permutations are possible. Hence on the numbered variant there are 16!/2 = 10,461,394,944,000 = 1.0·1013 positions.
In the coloured variant there are 4 sets of 4 identical pieces, and hence there are 16!/4!4 = 63,063,000 positions.

I have calculated God's Algorithm to find out how many moves each position needs to get solved. This is for the version with diagonally split tiles. A move in this context is any of the 12 ways of cycling seven tiles, as explained in the solution. The solved position has a pattern of concentric diamonds. It shows that it can always be done in at most 13 such cycles (10.005 on average).

Depth   Positions
01
112
293
3636
44,174
526,808
6165,092
7917,693
84,071,834
912,552,545
1023,737,340
1118,619,383
122,938,388
1329,001
Total   63,063,000

Notation:

Let T mean the pushing in of the top plunger, and let t mean releasing it. Similarly, let A, B, C, D denote the side plungers from top to bottom, with a capital letter meaning pushing it in and a small letter releasing it.

Useful Sequences:

Throughout the solution we need the following move sequences which cycle round 7 of the 8 tiles of the top two rows:
1a. Cycle all but top left tile clockwise: TBtb
1b. Cycle all but top left tile anti-clockwise: BTbt
2a. Cycle all but top right tile clockwise: ATBtba
2b. Cycle all but top right tile anti-clockwise: ABTbta

These sequences can also be performed on any other pair of adjacent rows.

Solution to the "It" puzzle

Phase 1: Solve the first tile of the top row.

  1. Find tile 1.
  2. If it lies somewhere in the bottom row then apply 1a on the bottom row (i.e. TDtd) until it is in the third row.
  3. If it lies somewhere in the third row then apply 1a on the third row (i.e. TCtc) until it is in the second row.
  4. Apply 1a or 1b until tile 1 lies at the left of row 2.
  5. Apply 2a to place the tile correctly.

Note that the method used in b-c above to bring up a tile to the desired row will be used whenever necessary in later phases without further explanation.

Phase 2: Solve the rest of the top row.
In this phase we will use 1a to successively place tile 4, 3 and 2 at the second position of the first row.

  1. Tile 4: Bring up tile 4 to the top rows if necessary. Then use 1a or 1b until it lies at (1,2), i.e. in row 1 column 2.
  2. Tile 3: If it lies in the top row, then perform 1a until it is in the second row, do 1a on the second/third rows to bring it down further, and perform 1b until tile 4 is back in column 2.
    Use 1b on the second/third row until it is in column 2.
    Use 2b on the second/third row to bring it to column 1.
    Use 1a on the first/second row to bring it to row 1, column 2, displacing tile 4 to column 3.
  3. Tile 2: A similar method as for tile 3 is used:
    If it lies in the top row, then perform 1a until it is in the second row, do 1a on the second/third rows to bring it down further, and perform 1b until tile 3 is back in column 2.
    Use 1b on the second/third row until it is to column 2.
    Use 2b on the second/third row to bring it to column 1.
    Use 1a on the first/second row to bring it to row 1, column 2, displacing tile 3 to column 3.

Phase 3: Solve the second row.
This is done using exactly the same method as the first row.

Phase 4: Solve tiles 15 and 16.

  1. Do any of 1a/1b/2a/2b on the bottom rows until tile 16 lies in column 4, row 3.
  2. Do 2a or 2b on the bottom rows until tile 15 lies in column 4, row 4.
  3. Do 1a, and tiles 15 and 16 will be placed correctly.

Phase 5: Solve tile 13.

Depending on its position, do one of the following:
Row 3, column 1: Do 1a, 2b.
Row 3, column 2: Do 1b three times, 2a twice.
Row 3, column 3: Do 2b twice, 1a three times, 2b once.
Row 3, column 4: Do 2a twice, 1a twice, 2a twice.
Row 4, column 1: Do nothing.
Row 4, column 2: Do 1a twice, 2b twice.

The final phase below uses three new sequences on the bottom two rows:
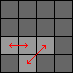
3a.
 		 Do 1b three times, 2a twice, 1a twice, 2b twice:
[Swaps pieces (3,1)-(3,2) and (3,3)-(4,2).]		 DTdt DTdt DTdt C TDtd TDtd c TDtd TDtd C DTdt DTdt c
 
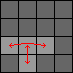
3b.
 		 Do 1b three times, 2b three times, 1b once, 2b once:
[Swaps pieces (3,1)-(3,3) and (3,2)-(4,2).]		 DTdt DTdt DTdt C DTdt DTdt DTdt c DTdt C DTdt c
 
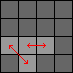
3c.
 		 Do 1a once, 2a once, 1b twice:
[Swaps pieces (3,2)-(3,3) and (3,1)-(4,2).]		 TDtd C TDtd c DTdt DTdt
 

These sequences do not move the tile at row 3 column 4, and make two swaps amongst the remaining four unsolved tiles.

Phase 6: Solve the remaining tiles.
It is always possible to get one of the positions in the table below (or if you're lucky even to solve it) by doing one of the sequences 3a-c. Then do the sequence shown in the table.
If this places tile 12 correctly, then you can now solve it by applying one of 3a-c.
If tile 12 was correctly placed before, then the sequence from the table will have moved it out, and you will have to repeat this phase once more to solve the puzzle.

 14 10 11  9    11  9 14 10    10 14  9 11     9 11 10 14
    12             12             12             12

 14 10  9 12    14  9 11 12
    11             10
 Perform TCtc, 3a, CTct.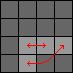 
 10 12 11  9     9 12 14 10    14 12  9 11    11 12 10 14
    14             11             10              9

 10 11  9 12    10 14 11 12     9 14 10 12     9 11 14 12
    14              9             11             10
 Perform TCtc, 3b, CTct. 
 11 10 12  9    14  9 12 10     9 14 12 11    10 11 12 14
    14             11             10              9

 11  9 10 12    11 10 14 12
    14              9
 Perform TCtc, 3c, CTct.