CUBIC CIRCULAR
A quarterly newsletter for Rubik Cube addicts
Issue 2 Spring 1982
| CONTENTS | | | |
| Introduction | | 2 | |
| News | | 2 | |
| New Books | | 3 | |
| Newsletters | | 3 | |
| Competitions, Times, etc. | | 3 | |
| Lead Hazards ? | | 4 | |
| Other Medical Anecdotes | | 6 | |
| Technical Notes | | 8 | |
| Sliding Piece Puzzles | | 9 | |
Published by David Singmaster Ltd., London, England. ISSN NO 0261-8362
2
INTRODUCTION
As usual, I am a bit behind with this. The last few months have been very hectic as
David Singmaster Ltd. has gotten launched. We had a stand at the London Toy Fair, I went
to the Nuremberg Toy Fair and Jane Nankivell went to the Paris Toy Fair. I counted about
50 new puzzles which will appear this year: A report on some of these will occupy most of
this issue. There are many other new products which will have to wait for the next Circular.
I have spent a lot of time reorganizing my bibliography and my files of material. The
bibliography now has some 900 items and runs to 35 pages. And I haven't had time to enter
several hundred items which were kindly passed on by Ideal Toy's public relations firm,
Porter, Le Vay & Rose. As a result, I haven't gotten very far into the 500 or 1000
letters on my desk, but I think I will be able to get to them soon... The technical material
on the Cube is already enough to fill another Circular, so perhaps the next one will be a
bit early. Meanwhile, don't despair if your pretty pattern or one-handed upside down record
isn't mentioned in this issue.
As you will see from the supplementary catalogue enclosed, we have taken on a large
number of new products. We intend to stock a large range for mail order and we will
emphasise products which are not widely available. If you know of an interesting product,
please tell us about it. We are looking out for a shop or warehouse with display area where
you will be able to come and look around.
We are developing a great range of contacts in the puzzle industry and have begun to act
as agents or manufacturers for several inventors. We can either arrange to manufacture on a
small scale or pass on ideas to major producers such as Mèffert or Pentangle. At the
moment, this is a new area of the business and we are feeling our way, but we would be
delighted to hear ideas from any readers.
NEWS
Ernő Rubik was awarded the Order of Labour Gold Class by the Hungarian government
in December.
Congratulations to Ernő and Rozsa Rubik on the birth of a son, Ernö III, on
26 December.
Rubik's Cube won the UK Toy of the Year award in January, the only product to win two
years in a row. (Lego won two years in a row, but with two products.)
Rubik's Cube has even made the Times Crossword. On 19 Jan 82, clue 14 down was "Modern
problem, to 23 colours on six sides (6,4)". Clue 23 across was "Act to stop official
race-meetings (9)" with answer 'segregate'.
I had the pleasure of meeting the man who invented the name "Rubik's Cube" in December.
Stewart Sims, senior vice-president for marketing and product development at Ideal Toy
Corp. in New York, was the contact man for getting the cube for Ideal. Both Gordian Knot
and Inca Gold had been suggested, but Sims didn't like them and Rubik's Cube came to him
after a few days.
3
New Books
Alexander (Sandy) H. Frey, Jr., has adapted my Notes into a school/college level text
for learning group theory and cube theory. This expands on the ideas covered in the Notes
so as to bring the ideas within reach of more students at this level. It is titled
"Handbook of Cubik Math" and is published by Endow Publishers (New Jersey). Lutterworth
Press is distributing it in the UK. (I should have called this the 'Cubik Circular'.)
John Ewing and Czes Kośniowski have produced "Puzzle it Out - Cubes, Groups and
Puzzles" which also presents the basics of group theory and applies them to several
puzzles. It is about the same length as the Notes, going less deep but covering the
basics in more detail. It falls about halfway between the Notes and the Handbook as regards
level.
Rubik has edited a book "A Bűvös Kocka" which is being done in English by Penguin
later this year. Rubik contributes a 19 page description of how he invented the Cube. The
major chapter are by Tamás Varga and Gerzon Kéri, with contributions on
physics from György Marx and on psychology from Tamás Vekerdy, and a foreword
by myself.
Jack Eidswick has produced a Rubik's Cube Engagement Calendar for 1982. (Available for
$6.95 from And Books, 702 South Michigan, South Bend, Indiana, 46618, USA.) This reveals
that Rubik was born on 18 June 1937 and that the first working model of the Magic Cube was
made by Rubik on 24 Oct 1973. Both of these are somewhat different than I have heard
before. I believe Rubik was 37 last year which gives a birth year of 1944. Rubik said he
invented in the late spring/early Summer of 1974, but he does not give any specific dates
in his book and possibly he doesn't have the dates clearly in mind.
Newsletters
Rubik is starting a quarterly to be called "Rubik's - Logic and Fantasy Dimensions".
It will be 52 pages, with colour, at $2.50 per issue or $9 per year from Lapkiadó
Vállalat, Kereskedelmi Iroda, H-1906 Budapest, POB 023, Hungary. The first issue
is planned for April. They may decide to use distributors in various countries
Ideal Toy Corp. is planning a Rubik's Cube Fan Club with a quarterly newsletter.
However, I haven't yet seen details. (I think something got lost on my desk.)
Anneke Treep and Just van Rossum have beat us all by starting a newsletter (in Dutch)
last August. It costs 9.50 Dfl per year from Anneke Treep, Folkert Postlaan 15, 1391 AV
Abcoude, Holland. The first issue had 4 pages.
Competitions, Times, etc.
Julian Chilvers, age 15, from Norwich, won the UK Championship on 12 December. He
clocked 25.79 seconds, a world record, on his third and final trial. He also had the
second best time, 28.36 seconds, on the second trial. He reports that he uses ordinary
car grease as a lubricant. He does the corners first, then completes most of the top and
bottom, then the middle. One contestant's cube flew apart. Another said he didn't like
Vaseline as it ran out when his cube 'got hot'. How fast was he turning it?? One contestant
had sweatbands on his arms, but he confessed it was mostly to frighten the opposition. Nial
Ferguson, the Irish champion, was, at age 20, the oldest competitor. He wore gloves between
trials to keep his hands warm.
4
The US Championship was done on a TV show "That's Incredible", recorded on 13 November
and broadcast on 7 December. Minh Thai, a Vietnamese refugee, age 16, won in a time of
26.04 seconds. The first prize was $2000 plus the trip to the World Championships. Second
place went to Jeffrey Varasano with a time of 28.96 seconds. Jeffrey holds the US record
with a time of 24.67 seconds in the Eastern Regional Competition.
The World Championships have been announced for various times and places, but the most
recent statement is that they will be in Budapest on 5 June.
In Germany or Hungary, there is a film of a four year old doing the cube in under 30
seconds: The film appears to be and is intact. Can you figure out how it was made? (Answer
below.)
The Los Angeles Times (1 Nov 81) reports on the western US Cube-A-Thon and on three
year old Glenn Quackenbusch of Torrance, the youngest competitor. He nonchalantly solved
a cube before the contest but was rather bedazzled by the cameras in the competition and
failed to finish by the bell. "We didn't even teach him how to do it. He learned from
watching his brother", said his father.
Richard Hodson has improved his one-handed record to 82.51 seconds. I saw John White
do the cube behind his back with only one look after he started. A 17-year old from the
Midlands has been clocked at 24.56 seconds. His name is John Duffey.
Miscellany
Rubik's Cube has been placed in the design section of the Museum of Modern Art.
BCG's long awaited treatise "Winning Ways" has just appeared.
LEAD HAZARDS?
In C1-10, I reported that the genuine Pyraminx used special lead-free labels while the
Taiwanese imitations used labels with a lead level higher than would be permitted for a
'paint film' under The Toys (Safety) Regulations 1974. These limit lead to 2500 parts per
million (ppm) in the dry paint film and "'paint' includes lacquer, varnish and other
similar substances". We wrote to all the Trading Standards Offices in the UK about this in
the autumn. Despite considerable interest and some resulting media coverage in the
Midlands, no Trading Standards Officer felt the phrase "other similar substances" could be
stretched to cover plastic labels, although the Consumer Safety Unit which drafted the
regulations indicated they would have included plastic labels if they had existed in 1974.
Recently, Bill Yoxall, Chief Trading Standards Officer for Southwark, has gone out and
analysed all the colours on 9 different cubes and similar products, including Ideal Rubik
Cubes from Hungary and Hong Kong, though he did not test a genuine Pyraminx. Wonderful
Puzzler (Taiwan), Key Chain Magic Puzzle (Taiwan), Rubik's Cube (Hong Kong), Elliptical
Puzzle (??), Rubik's Cube (Hungary), Diamond Puzzler (Taiwan) all had lead levels between
26,250 and 32,900 ppm in their yellow labels. All of these except the Rubik's Cube (Hong
Kong) had between 6,700 and 9,800 ppm in their green labels. Elliptical Puzzle had 9,000
ppm in red labels, Wonderful Puzzler and The Pyramids (Taiwan) had 7,800 to 8,900 ppm in
their orange labels. (The Pyramids uses gold labels instead of yellow. Diamond Puzzler is
a pirate version of Mèffert's Pyraminx Octahedron.) The puzzles with no lead were
Face Four (Hong Kong) and Mind Exerciser (Japan) which are Instant Insanity type puzzles.
These results are given in a news release "Rubik Cubes Danger", Southwark Public Relations,
Town Hall, Peckham Road, London SE5 8UB, 2pp., 4 March 1982.
5
At first glance, these lead levels are quite horrific and I am amazed that the Hungarian
Rubik Cubes are as bad as the others. However, two questions immediately arise.
- Do children eat them?
- Is the lead in PVC labels locked into the plastic in such a way as to be inert?
A. Many people have said that they have seen cubes used as dummies (i.e.
pacifiers) and that cubes are often left about where infants can chew on them. Several
friends have shown me cubes which have been chewed by their infants. One person saw a
child in a pram whose only word seemed to be 'Rubicube'! Still, the cube is not intended
as a toy for children of this age.
B. At first I could get no answers to this question. I eventually got in touch
with Professor Bryce-Smith of the Department of Chemistry at the University of Reading.
He informed me that the Water Research Association had discovered that lead dissolved out
of unplasticized PVC pipes into cold water and that a colleague had discovered that cadmium
dissolved out of a popular child's plastic building block with saliva. (The manufacturers
of the blocks promptly changed the composition of the plastic.)
The results of Southwark' s analyses show that the lead is used as a pigment rather
than a PVC stabiliser. The PVC water pipes were probably uncoloured (I haven't seen the
reports yet), but a chemist colleague tells me that lead stearate is often out in PVC
soapy surface for release from moulds. This may explain problem of the water pipes, but
the fact remains that at least one form of lead can dissolve out of the PVC.
Apparently, there are no other results, so we don't really know the answer to question
B, but these results would certainly indicate that the same lead level as in paint film
would be prudent for plastic.
My advice is -
Don't let infants chew on cubes or imitation pyramids:
I have since spoken to Mèffert who reaffirms that all his colours are lead-free
and that they are checked to be below 10 ppm, a level which occurs in some tinned foods
and below which it 15 difficult to test.
6
OTHER MEDICAL ANECDOTES
'Cubist's Thumb' is apparently the same as 'Disco Digit'. It has finally made it into
the New England Journal of Medicine (mid Sept., 1981). Douglas Waugh, a Canadian doctor,
got it in the same way as Dame Kathleen Ollerenshaw (N38). Though right-handed they hold
the Cube firmly against the left palm with a corner pressing into the heel of the thumb.
Dr. Waugh's doctor first diagnosed it as gout! But the true cause was soon revealed and
Dr. Waugh attributes it to using a cheap Taiwanese Cube and prescribes a proper Rubik's
Cube as a cure. Incidentally, Dame Kathleen is fully recovered from her operation and says
that her doctor was most pleased to have her as a patient so he could learn how to do the
Cube from her.
David Laine writes to New Scientist (14 May 81) that his 17 year old son gets fits and
has twice passed out while doing the Cube! He is otherwise healthy. Brain strain??
On the positive side, Eric Pfisterer of Toronto (the same one) reports that the Cube has
cured his Tennis Elbow. My tennis-playing friends thought this must be because he left off
tennis for so long, but he replies that similar hand exercises are standard treatment for
the condition.
My brother-in-law, John Rowland, reports the Cube helped him stop smoking! "I reach for
a Cube instead of a cigarette." However, Karen Rowland says it makes her smoke more!
On 7 Jan 82, P. J. Voas wrote to the Guardian about strange afflictions and inquired
"Can anyone suggest a medical name for the marks caused by sitting down heavily on a
discarded Rubik's Cube?" Needless to say, several readers wrote to the rescue.
J.A. Norris: "contused cubum";
Malcolm Ferguson: "glutaeous Rubicus" or "Rubik's bum";
Martin Davis: "Arsickness". (He points out that cubes left on the floor can cause "Rubato".)
Robert Goodden: "fundamental rubikundity".
However, this doesn't compare in seriousness to sitting on a Pyraminx!! (Get the point!)
Indeed, I don't really recommend you put the new Pyraminx key-chain in your pocket. You
might do yourself an injury!
Rubik Cubes have been banned from Bath High School as a safety hazard. "They bump into
each other and fall over objects while concentrating on the Cubes", said Headmistress
Doris Chapman.
Two rather moving stories have been reported. I met a doctor at a record fair who said
he worked in a teenage leukaemia ward where there was a pressing need to distract the
teenage patients. He said the Cube was the best distraction he had ever had.
A mother wrote to the Daily Express that her 14 year old daughter, who is severely
handicapped, has learned how to do the Cube - much to her delight and the amazement of
the rest of the family. "It's the first thing she's ever been able to do that so many
normal children can't."
7
I gave a Cube to a neighbour named John in the early days of the Cube. A few days
later, the friend in the next flat reported that "They have taken poor John away. You
know that Cube you gave him? Well, he's been awake ever since and this morning he just
went 'Aargh' and we had to call the police. Please, could I have twenty more Cubes?"
Henry Ernest Dudeney, writing about the craze produced by Sam Loyd's
15 Puzzle in 1873, says: "And it has been stated, though doubtless it was
a Yankee exaggeration, that some 1500 weak-minded persons in America alone
were driven to insanity by it." My partner, Jane Nankivell, suggested the
slogan that we use on our tee and sweat shirts: "Rubik's Cube Cures Sanity".
Fortunately we have not yet heard of any real cases, though I have received
a number of crank letters and phone calls.
There are rumours that American psychologists are using the Cube in aptitude testing.
Fred Warshofsky reports that a Viennese psychiatrist gives cubes to his patients. They all
do it, and the way they do it seems to have little psychological significance. However,
about half lie about how long it took them to do it.
8
TECHNICAL NOTES
H. J. Kamack and T. R. Keane have sent a 43 page article on the Rubik tesseract, i.e.
the 34 'Cube'. They allow each of the 8 3-dimensional faces to rotate as a
solid in its own 3-dimensional space, so each face has 24 positions. Using a computer
simulator, they found sufficient processes to generate all positions subject to some
conservation laws. The laws are a bit too complex to explain here since one must introduce
all the terminology for parts of a 4-dimemsional cube and for rotations in 3-space. If we
note that a 34 has 81 pieces comprising 16 0-dimensional corners, 32
1-dimensional 'edges', 24 2-dimensional 'squares', 8 3-dimensional faces and 1
4-dimesional cube and that an i dimensional piece has 4-i outside 3-dimensional facets,
then the following formula for N, the number of achievable patterns, will show the
conservation laws to some extent.
N = (24!·32!·16!)/4 · (224/2) · (632/2) · (1216/3) =
1 75677 28807 09135 84316 85260 79081 02505 96144 84630 14955 76514 77156
02173 32367 98970 16855 06002 74887 65008 23542 07129 60000 00000 00000
= 1.8 × 10120, which they describe as about the number of ways to play a game of
chess. (The astute reader will wonder how this number was computed to 121 places. I have
written a multi precision calculator routine for my Sinclair ZX81 and it only took about five
minutes work to compute this. This is the largest example I have yet done.)
In the draft English version of his chapter for Rubik's book, G. Marx remarks that the
cube has 12 positions after one move, 114 after two moves, 1068 after three and 10011
after four and he credits these numbers to Zoltán Kaufmann. After some
contemplation, I realised that he was counting 90° moves, e.g. R2 is counted
as two moves. By considering all 15 (= 42-1) moves on an axis and the number
of 90° moves they use, I find that the number Sn ,of sequences of moves with
obvious redundancy removed, satisfies: Sn = 8 Sn-1 + 12 Sn-2
+ 8 Sn-3 + 2 Sn-4 for n>=5. For smaller n, the sum terminates at
S0 (= 1) and its coefficient is multiplied by 3/2 since there is no previous move
to be on a different axis from.
Letting Tn = S0 + S1 +
S2 + ... + Sn, we get Tn > N first at n = 21, where
S21 = 3.3 × 1020, T21 = 3.7 × 1020.
We have Tn = 1.45 (9.37)n. The previous analysis (N34) gave
Tn = 1.47 (13.35) n, with critical value n = 18. I find it
remarkable that the critical value for 90° turns not much larger. The asymptotic results
for T indicate that n turns of 90° or 180° are equivalent to about 1.155 90° turns.
The 43 are in production. Discussion with David Collins (who, with Daniel
Smith, also devised a mechanism for the 43 has clarified the number of possible
patterns. At line 14 of C1-7, the number of patterns in the 43 supergroup is
divided by 247 when solid coloured faces are used. We cannot interchange the
identical edge pieces because then they are both flipped and the result is not the same
as before exchanging them. There is an extra factor of 24 because the lack of centres
means we don't know which way is up. Thus we now set 8!·24!·24!·38 /
2·3·247 = 3 70059 84207 82450 93493 70469 87249 28716 80000 00000 =
3.7 × 1045.
Ideal is advertising 363 octillion, meaning 363 × 1048,
which is probably 24·212 the number we have found. This would arise if they
forgot the fact that there are no centres (as I did also) and did not notice the edge
orientation properties. Indeed, their number is 1/6 of the number in line 8 on C1-7.
Still compared to their results on the 33, this is a pretty good result.
9
SLIDING PIECE PUZZLES
The distant ancestor of all the sliding piece puzzles which are now appearing is Sam
Loyd's 15 Puzzle of 1873, which had 15 square pieces in a 42 frame.
Three major types of puzzles have appeared since early 1981, which fill in the huge conceptual
gap between the 15 Puzzle and Rubik's Cube. Surprisingly, they have appeared in the
reverse of what I consider logical order. More recently, several new types of interlocking
cycle puzzles and switchable cycle puzzles have appeared. In this essay, I will discuss
these puzzles and give the number of patterns in each case. Many other puzzles are also
appearing, but I will treat them in a later issue.
4 × 4 and CROSSOVER
These are the most recent and I have only seen a sample of each. They have a 42
frame with concealed extra spaces at each end of each row and column, so there are 32
spaces in all. Each row and column has 5 pieces in it, which can be slid back and forth
to expose two different groups of 4. The 4 × 4 puzzles from Tsukuda (Japan) have several
columns locked together to complicate things and they come with three kinds of marking.
Crossover, from Nintendo (Japan), has all rows and columns separately moveable, but the
pieces and the glass covers are polarised so a piece changes from dark to light as it
moves: One can make the square all dark or all light.
The group structure here as with the 15 Puzzle, is somewhat concealed. One must consider
just the positions where the rows and columns are slid to the same configuration one began
at. Otherwise one cannot combine processes. To get all the rows and columns back, each must
be slid back as often as forward. If we consider each slide as an action on all 32
positions, each one is a 6-cycle and an even number of these must be an even permutation of
the 32 positions. When we put all the slides back, the 8 positions containing no piece are
restored to their original places, so our move must be an even permutation of the 24 pieces.
Thus there are 24! / 2 = 3102 24200 86661 97196 80000 patterns of the 24 pieces when they
are all distinct. However, the 8 concealed pieces can be permuted in 8! / 2 ways which
cannot be seen, so there are 24! / 8! = 15388 10520 17172 48000 visib1e patterns when the
pieces are all distinct. If we consider the 28 = 256 ways the slides can be
positioned, we get 39 39354 93163 96154 88000 patterns. With Crossover, each square can
only be dark or light, so there are only 216 = 65536 visible patterns and
considering the slide positions only gives 167 77216 patterns. At least in Crossover, we
find that the commutator of a row and a column move is a 3-cycle and there is enough
transitivity to get any 3-cycle by conjugation, so all the even permutations are achievable.
(Exercise - check this.)
SLIDING CUBE PUZZLES
In 1892, W. W. Rouse Ball, in Mathematical recreations and Essays, remarks, after a
discussion of the 15 Puzzle, "We can conceive also of a similar cubical puzzle, but we
could not work it practically except by sections." Apparently no one tried to make one
until Piet Hein came up with his elegant Bloxbox in 1973. This is 7 cubes in a 23
box and they are moved simply by tilting the box to let a cube slide into the blank space.
Recently several people, including both Rubik and myself have reinvented this both in
23 and 33 versions. I have seen five types in production and two
handmade versions as well as an example of Hein's which went out of production some time
ago. A 23 comes from Sakura (Japan) with cubes having their outsides coloured
in six colours and the inner faces all white.
10
The face colours can be seen edgewise which makes it much easier to tell where a piece
belongs. A more substantial and 'handy' version is exported by Konsumex, the main Hungarian
export agency and the exporters of the Cube. Their version is now available in the UK. Its
cubes have slightly inset circles containing either red or blue colour. This makes it much
more difficult to find out the colours on inner faces - one must manoeuvre the pieces to
see what the hidden colours are. Further it is not clear what colour pattern one is supposed
to achieve. The theory of these puzzles is the same as for the 15 Puzzle. To get the blank
space back where it began, one must make an even number of exchanges, so one only gets the
even permutations. The 23 thus has 7! / 2 = 2520 patterns with the blank in a
particular spot and 8! / 2 = 20160 patterns all together. One can obtain a type of 6-X
pattern but one cannot put all the outside faces to the inside.
A 33, called Puzzle Box, comes from K. W. Toys (Korea). It has letters on
one side of the 26 pieces (convenient:) so one can spell words. The 3 puzzles present a
new complexity - how do you move the pieces in the centres of the faces? Puzzle Box has
holes in the faces and a push stick, though one can also hold the pieces by pressing
fingers against the holes. A more elegant technique is to spin the cube, which sends
pieces to the corners leaving a blank at the middle of an edge. The spinning technique
can also move the piece in the centre of the cube with some ingenuity. (Exercise:) Again
one just gets the even permutations if the blank returns to its origin, so there are
26! / 2 = 20 16457 30563 30281 77920 00000 patterns then and 27! / 2 =
544 44347 25209 17608 03840 00000 patterns all together. On the 33, a number
of patterns like 6-Z, 6+ and 6-spot can be formed, but only one of the production forms
makes these recognisable.
The second 33 that I saw in production is the Hungarian analogue of their
23. This resolves the problem of moving centres by gluing all the centres
together to the cube centre! This takes a while to discover and it then determines the
'natural' pattern to achieve. But it takes quite a while and lots of concentration since
the pieces are hard to recognise and to keep track of. Further the fixed centres mean you
have to move things around 8-cycles.
The last 33 in production is called Mad
Marbles, from Lakeside (USA). It is modified with an internal column so there are only 24
positions. With grooves on this column, it is possible to use balls (= plastic marbles)
instead of cubical pieces. The balls come in only three colours, so this is a pretty easy
puzzle with 23!/8!·8!·7! = 31551 70590 patterns with the blank in place and
24!/8!·8!·7! = 7 57240 94160 patterns all together. Since the pieces have no
sides, one could not distinguish some patterns except by the label on the box. If the box
were the same on all sides, these numbers would have to be divided by about 8, but this is
a non-trivial calculation.
CYLINDRICAL PUZZLES
These are essentially a 15 Puzzle wrapped around a cylinder and various versions were
on the market last year. Because of gravity and for ease of handling, it is convenient to
consider the cylinder as horizontal. Pieces can slide horizontally. The cylinder is sliced
into a number of discs, which can rotate about the cylinder's axis. The simplest form,
called Whippit (and numerous other names) had three discs containing six positions. (I
will abbreviate this as 3 by 6.) Whippit has three pieces of five colours and two pieces
of a sixth colour, together with one blank position. I usually consider the blank as a
piece of the sixth colour for symmetry.
11
The analysis of such puzzles is easiest when all the pieces are distinct and the discs
are marked so one can recognise if they have returned to their original location. Then,
just as in the 15 Puzzle, if the blank and the discs are returned to their original places,
only the even permutations of the pieces are possible. Further, it is easy to construct a
3-cycle and there is sufficient transitivity so that all even permutations are achievable.
However, the discs are usually unmarked, so we do not consider the disc positions. Thus we
can make a single turn of a disc, which is a b-cycle. This is an odd permutation if and
only if b is even. So if b is even, we can also get the odd permutations of the pieces.
For a 3 by 6 puzzle with distinct pieces, we get 17! = 35568 74280 96000 patterns with
the blank in place and 18! = 6 40237 37057 28000 patterns all together. With Whippit, the
three pieces of each colour can be indistinguishably rearranged in 3! = 6 ways, so the
number of distinguishable patterns is 18!/3!6 = 13 72250 88000. (This is
multiplied by 3 if we distinguish the blank from the two pieces of the sixth colour,
giving 41 16752 64000 patterns.)
The next versions of the puzzle to appear were 6 by 6 ones from the Far East and
Hungary, then 4 by 4 and 5 by 5 ones also appeared. If all pieces of an a by b puzzle are
distinct and the discs are unmarked, we have (ab)! patterns all together when b is even and
half that many when b is odd. If we have a pieces of each of b colours, there are
a!b indistinguishable ways to rearrange pieces. If some a > 1, then half of
these are odd and unachievable when b is odd. In either case, we get (ab)!/a!b
distinct achievable patterns. The relevant numbers are given.
16! = 2092 27898 88000
l6!/4! 4 = 630 63000
25!/2 = 77556 05021 66549 29920 00000
25!/5! 5 = 62336 07431 25120
36! = 7 19933 26789 90121 74679 99448 15083 52000 00000
36!/6! 6 =26701 77736 63714 92473 08800
There are also 72 versions of the 15 Puzzle available, having 49!/2
= 304 14093 20171 33780 43612 60816 60647 68844 37764 15689 60512 00000 00000 patterns.
Remarks on difficulty
Many people tend to equate the difficulty of a puzzle with the number of possibilities.
But this is only true for puzzles of the same type. Even then, I feel the difficulty is not
proportional to the number of patterns but to something like the logarithm of the number of
patterns. If we have M moves at each step and N possibilities, then the estimated length of
a solution method ought to be given by ML = N or L = log N/log M. Thus a puzzle
of twice the difficulty has the square of the number of possibilities.
Another way to estimate difficulty is to determine the maximum number m of moves to
effect a minimal change such as a 3-cycle or a 2-cycle. If there are n pieces, then mn is
a measure of difficulty. I would expect m to increase with n, but not as fast as n. So our
difficulty might be measured by n log n or n3/2. The first is about the same as
our previous measure, since if N = n!, then log N ~ n log n by Stirling's approximation.
For example, in an n by n puzzle, there are n2 pieces but the maximum number
of moves required to produce an arbitrary 3-cycle is something like 6n. Thus we might
expect a difficulty of 6n3 while the previous analysis gives something like
2n2 log n.
12
However, these analyses are only for puzzles of the same type. A 7 by 7 has many more
patterns than Rubik's Cube, but it is vastly easier. There are several obvious ways in
which the Cube is more difficult than the puzzles considered above.
- The pieces have orientation. This imparts an extra twist to the group structure, so
we get a wreath product (N58-60).
- The pieces are of different types, but the types interact. This is why the group of
the cube is a subgroup of a direct sum (N58-59).
(Rubik has pointed out A, but I find B is also relevant.)
It is hard to quantify these or other points so one must fall back on some personal
measure such as how long it takes you to solve it.
Back to cylindrical Puzzles
Last year, a Hungarian 6 by 6 called Babylon Tower (or Tower of Babel) was popular in
Germany and France and it is now appearing elsewhere via Ideal Toy. This has six balls of
six colours, but they are gradated in intensity so all 36 are distinct. The blank space
is obtained by pressing a ball into one of two spring-loaded spaces in the base. This was
devised by Endre Pap - of whom more later.
6 by 6 versions of Whippit type with
numbers instead of gradated colours also appeared. A 4 by 4 and a 5 by 5 came from
Hungary but had an extra level with one position into which one ball could be pushed to
give the working blank.
Another 4 by 4, called Missing Link, was a popular product for Ideal in the US last
year and is now coming to Europe, though the Taiwanese imitations have been here for some
time. This has fifteen pieces of four colours with a chain link pattern which distinguishes
the end pieces, while the middle two are identical. The extra feature is that the
middle two discs are locked together. As with the Hungarian 33, this makes
movements more complex, but all 16! Patterns are achievable. Because there are two identical
pieces of each colour, there are 16! / 2!4 = 130 76743 68000 distinguishable
patterns. (If the blank is distinguished from the other middle pieces, we multiply by 2 to
get 261 53487 36000 patterns.)
But the most difficult of the cylindrical puzzles is the Ten Billion Barrel, invented by
Gumpei Yokoi of the Japanese firm Nintendo. This is a mixture of the 4 × 4 puzzles and the
cylinders. It is something like a 4 by 5 cylinder, but the two rotating discs contain two
balls of each row. There are three extra positions at each end, three extra balls and a
plunger which slides three rows back and forth by one position. To begin, we assume the
balls are all distinct. If one doesn't turn the barrel end for end, then the plunger must
operate an even number of times to get back to its original state and each disc turn is
an even permutation, so each pattern is an even permutation of the 23 pieces.
Turning the barrel end for end and making a plunge also gives the original configuration
and is an odd permutation. (Actually two blank positions are also exchanged.) Because of
the complexity of these moves, it is not easy to see how to achieve all the even
permutations, but it is possible, even with the two discs locked together! So we have
either 23! / 2 = 129 26008 36944 24883 20000 or 23! = 258 52016 73888 49766 40000
patterns depending on whether we preserve the end or not. Ten Billion comes with 4
balls of five colours and 3 balls of a sixth colour. These can be permuted in
4!5·3! ways (divided by 2 if we keep to the even permutations), so there are
23!/(4!53!) = 54111 17561 85000 distinguishable patterns. (NOTE. The figure
quoted in our catalogue has a misprint.) Despite having fewer patterns, most people find
this puzzle harder to solve than the Cube, but it doesn't grip people as much because it
is hard follow what is happening. Several authors have written about it, but most solutions
tend to show you one 5-cycle and then leave you to get on with it. Trevor Hutton is
preparing a detailed solution with pretty patterns and useful processes, etc.
13
OTHER TYPES
Beyond the above types of sliding piece puzzles, a number of related types have begun
to appear and may presage more of these types.
TRILLION
This is sort of a flat version of the Ten Billion and comes from Agatsuma (Japan). It
has 17 positions arranged in a cross in a circular frame. At the centre, the 5 innermost
pieces can be rotated (leaving the innermost piece fixed). Surrounding these, there is a
rotatable ring containing two pieces of each cross arm and an outer ring contains one piece
of each arm. One arm of the cross has a spring loaded plunger which slides the 9 pieces
along by one place. The plunger then blocks the outer ring from turning. Since some ring
turns are 4-cycles and one easily finds some pairs of 2-cycles, it is not hard to achieve
all 17! = 35568 74280 96000 patterns when the pieces are distinct. I have just completed
the solution and I find that the plunger and the middle ring generate a subgroup isomorphic
to the rigid motions of an octahedron on its vertices (or a cube on its faces). Trillion
comes with 4 pieces of 4 colours and one piece of a fifth colour, so there are only
17!/4!4 = 10720 71000 distinguishable patterns. Two of these are fairly
natural: Rings - with odd piece at the centre and the rings having the colours shown on
the puzzle; Cross - with the odd piece in the centre and the arms of solid colours.
INTERLOCKING CYCLE PUZZLES
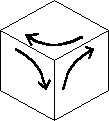 All of the above puzzles have either blank positions or auxiliary positions. Rubik's Cube
has no such blanks, so any sequence of moves can be combined with any other sequence. Thus
the set of all patterns is the group of interest, rather than the set of patterns which
leave the blanks or auxiliaries fixed. If one considers just two or three faces of the
33, e.g. <F,R> (N55-57) or <F, U, R>, then one has two or three
interlocking 4-cycles which can be drawn on a plane as in the diagram. About a year ago, I
began to contemplate planar puzzles with this structure, but I never got very far. I
believe the analysis of sliding piece puzzles with one blank on a general graph has been
done and will appear in Winning Ways (= BCG) which has just appeared (though I haven't
seen one yet). I am not sure if this also does the interlocking cycle puzzles.
Dan Sleator, now at Bell Labs, pointed out to me a number of
ways such puzzles can be built and several independent versions have now appeared.
All of the above puzzles have either blank positions or auxiliary positions. Rubik's Cube
has no such blanks, so any sequence of moves can be combined with any other sequence. Thus
the set of all patterns is the group of interest, rather than the set of patterns which
leave the blanks or auxiliaries fixed. If one considers just two or three faces of the
33, e.g. <F,R> (N55-57) or <F, U, R>, then one has two or three
interlocking 4-cycles which can be drawn on a plane as in the diagram. About a year ago, I
began to contemplate planar puzzles with this structure, but I never got very far. I
believe the analysis of sliding piece puzzles with one blank on a general graph has been
done and will appear in Winning Ways (= BCG) which has just appeared (though I haven't
seen one yet). I am not sure if this also does the interlocking cycle puzzles.
Dan Sleator, now at Bell Labs, pointed out to me a number of
ways such puzzles can be built and several independent versions have now appeared.
14
HUNGARIAN RINGS
 This idea is due to Endre Pap and three coworkers. The simplest version which is the
only one that has yet appeared, has two intersecting rings of 20 balls (hence 38 all
together). At the intersections, which are five balls apart, a ball can move with either
ring. The puzzle seems quite simple. The commutator of the two ring moves is a pair of
3-cycles, but it takes some time and effort to find elementary processes such as a pair
of 2-cycles, and a solution strategy. Since a ring turn is a 20-cycle, which is an odd
permutation, one can get all 38! = 52302 26174 66601 11176 00072 24100 07429 12000 00000
patterns when the pieces are distinct. The puzzle comes with 10 balls of each of two
colours and 9 balls of two other colours, so there are then
38!/(10!·10!·9!·9!) = 3 01625 69686 36903 99200
distinguishable patterns. With so many identical pieces, it is hard to keep track of the
position of a ring. I wrote a computer simulation to make it easier! There are several
suggested patterns in the instructions. The original pattern as solid coloured arcs as
shown. The most difficult has two colours alternating on each ring. Dan Sleator tells
me there is a 19th century patent on this idea, but the present exemplification has
differences which may justify a new patent. I gather that several variations with more
rings will appear. A different two ring version has been invented by Ivan Moscovitch,
the noted Israeli inventor of puzzles. Perhaps we should call this a bicycle?
This idea is due to Endre Pap and three coworkers. The simplest version which is the
only one that has yet appeared, has two intersecting rings of 20 balls (hence 38 all
together). At the intersections, which are five balls apart, a ball can move with either
ring. The puzzle seems quite simple. The commutator of the two ring moves is a pair of
3-cycles, but it takes some time and effort to find elementary processes such as a pair
of 2-cycles, and a solution strategy. Since a ring turn is a 20-cycle, which is an odd
permutation, one can get all 38! = 52302 26174 66601 11176 00072 24100 07429 12000 00000
patterns when the pieces are distinct. The puzzle comes with 10 balls of each of two
colours and 9 balls of two other colours, so there are then
38!/(10!·10!·9!·9!) = 3 01625 69686 36903 99200
distinguishable patterns. With so many identical pieces, it is hard to keep track of the
position of a ring. I wrote a computer simulation to make it easier! There are several
suggested patterns in the instructions. The original pattern as solid coloured arcs as
shown. The most difficult has two colours alternating on each ring. Dan Sleator tells
me there is a 19th century patent on this idea, but the present exemplification has
differences which may justify a new patent. I gather that several variations with more
rings will appear. A different two ring version has been invented by Ivan Moscovitch,
the noted Israeli inventor of puzzles. Perhaps we should call this a bicycle?
DISC CHESS, ROTASCOPE, Etc.
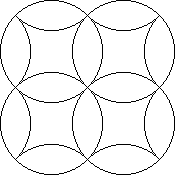 If one thinks about planar cycles with solid pieces instead of tails, there are many
possible patterns, but the pieces start getting fiddly. Dan Sleator suggested the
following, which may be produced by Mèffert. Consider the diagram of four circles.
Each circle can rotate and this permutes the 12 'lens' pieces. The structure of commutators,
etc. are easy to see here because of the planarity and one easily gets al 12! = 4790 01600
patterns. The even valency at the centre guarantees that no orientation changes occur.
Mèffert's prototype has 6 circles in a 3 by 2 array, giving 17 pieces and 17! =
35568 74280 96000 patterns when all the pieces are distinct. But the prototype has 3 pieces
of 3 colours and 2 pieces of 4 other colours, giving
17!/(3!3·2!4) = 10 29188 16000 distinct patterns.
I am told of a game by Milton Bradley (?) called Turntables (?) which used the same
mechanism. (There is no new thing under the sun!)
If one thinks about planar cycles with solid pieces instead of tails, there are many
possible patterns, but the pieces start getting fiddly. Dan Sleator suggested the
following, which may be produced by Mèffert. Consider the diagram of four circles.
Each circle can rotate and this permutes the 12 'lens' pieces. The structure of commutators,
etc. are easy to see here because of the planarity and one easily gets al 12! = 4790 01600
patterns. The even valency at the centre guarantees that no orientation changes occur.
Mèffert's prototype has 6 circles in a 3 by 2 array, giving 17 pieces and 17! =
35568 74280 96000 patterns when all the pieces are distinct. But the prototype has 3 pieces
of 3 colours and 2 pieces of 4 other colours, giving
17!/(3!3·2!4) = 10 29188 16000 distinct patterns.
I am told of a game by Milton Bradley (?) called Turntables (?) which used the same
mechanism. (There is no new thing under the sun!)
15
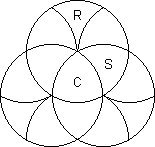 Rotascope is an unsymmetric approach to a triangular version of the above. Here the
pieces are not all the same, so rotation of one disc can block other rotations. The set of
patterns is not a group - one must consider just the patterns with the centre (C) and the
rims (R) fixed. Exercise 1. The rims cannot be permuted. Thus we get just permutations of
the 9 shields (S) and a counting argument shows we only ever get the even permutations of
these, i.e. 9!/2 = 1 81440 patterns. All these are achievable. Exercise 2. The shortest
process leaving the rims and centre fixed is 8 moves long. Exercise 3. The centre cannot
be twisted by itself.
Rotascope is an unsymmetric approach to a triangular version of the above. Here the
pieces are not all the same, so rotation of one disc can block other rotations. The set of
patterns is not a group - one must consider just the patterns with the centre (C) and the
rims (R) fixed. Exercise 1. The rims cannot be permuted. Thus we get just permutations of
the 9 shields (S) and a counting argument shows we only ever get the even permutations of
these, i.e. 9!/2 = 1 81440 patterns. All these are achievable. Exercise 2. The shortest
process leaving the rims and centre fixed is 8 moves long. Exercise 3. The centre cannot
be twisted by itself.
Rotascope is the first of a series of similar puzzles invented a few years ago by a
French inventor, Raoul Raba.
Interestingly, the same idea won first prize last year in a
Hungarian puzzle Invention competition chaired by Rubik. Rubik says they are the same, but
perhaps there is some difference?? Rotascope is being produced by Pentangle.
EQUATOR
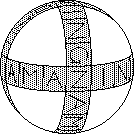 This is another Hungarian production exported by Konsumex. It has three interlocking
cycles arranged as orthogonal great circles on a sphere. Each cycle has 12 square pieces,
making 30 in all. These occur in 15 antipodal pairs. The pairs can be permuted in 15! ways
and each pair can be inverted, giving 15!·215 = 42 84987 36906 24000 positional
patterns. However the square pieces have four sides which can be distinguished. By carefully
shifting a piece around three sides of a triangle, on can twist one piece. (Its antipode
twists oppositely which satisfies the conservation law.) Hence there are
15! 215·415 = 4 60097 01534 74022 5458l 76000 patterns
if the pieces and their sides are distinct. On the puzzle as a supplied, four sectors of the
sphere are coloured say with A, B, C, D, with the colour boundaries along cycles. This
gives 1 4-coloured pair, 10 2-coloured pairs, and 4 1-coloured pairs. (A 1-coloured pair
has its two pieces each 1-coloured but of different colours, etc.) The 2-coloured pairs
are of only two types: AB opposite CD and BC opposite DA. Likewise the 1-coloured pairs
are of only two types: A opposite C and B opposite D. This gives
15!/(1!·5!·5!·2!·2!) · 215·411·14 = 3120 23258 02097 04960 distinct patterns.
This is another Hungarian production exported by Konsumex. It has three interlocking
cycles arranged as orthogonal great circles on a sphere. Each cycle has 12 square pieces,
making 30 in all. These occur in 15 antipodal pairs. The pairs can be permuted in 15! ways
and each pair can be inverted, giving 15!·215 = 42 84987 36906 24000 positional
patterns. However the square pieces have four sides which can be distinguished. By carefully
shifting a piece around three sides of a triangle, on can twist one piece. (Its antipode
twists oppositely which satisfies the conservation law.) Hence there are
15! 215·415 = 4 60097 01534 74022 5458l 76000 patterns
if the pieces and their sides are distinct. On the puzzle as a supplied, four sectors of the
sphere are coloured say with A, B, C, D, with the colour boundaries along cycles. This
gives 1 4-coloured pair, 10 2-coloured pairs, and 4 1-coloured pairs. (A 1-coloured pair
has its two pieces each 1-coloured but of different colours, etc.) The 2-coloured pairs
are of only two types: AB opposite CD and BC opposite DA. Likewise the 1-coloured pairs
are of only two types: A opposite C and B opposite D. This gives
15!/(1!·5!·5!·2!·2!) · 215·411·14 = 3120 23258 02097 04960 distinct patterns.
Trevor Truran reports that Christiaan Freeling has also invented a puzzle of this type
with 14 pieces in each groove, but he was unable to get anyone to produce it. Freeling's
ball is shown above. Truran contemplates the puzzle with the hemispheres free to turn,
which will lead into the next type of puzzle.
16
SWITCHABLE CYCLE PUZZLES
This group of puzzles has several disjoint cycles but the cycles can be broken and
rejoined in various ways.
ORB-IT
This is a sphere with 4 equally spaced horizontal grooves containing 8, 20, 20, 8 pieces.
One half of the sphere rotates on a vertical plane in multiples of 45°. A 45° turn gives
one 'swirl' cycle of 56 pieces and a 90° turn gives two 'tennis ball' cycles of 28 pieces.
I find that the basic trick used in the Magic Domino (N35) will give a 3-cycle, so all 56!
= 71099 85878 04863 45185 40456 47463 72494 97364 97978 88116 84586 87447 04000 00000 00000
patterns are achievable when the pieces are distinct. The puzzle comes with 8, 20, 20, 8
pieces of four colours, so there are 56!/(8!·20!·20!·8!) = 7388 87734 75012 11308 95230 51000
distinguishable patterns. The puzzle as a whole has 8 symmetries which gives about 1/8 as
many distinguishable patterns, but this is a non-trivial calculation, best done by use of
Burnside's Lemma and I have not done this. (The same applies to the next two puzzles.)
Orb-It was invented by Chris Wiggs, an English designer, and has been developed with Tom
Kremer. They are producing it in the UK.
DIOGENES
This was invented by Hubert Petutschnig, an Austrian engineer. It is a 3 by 10 cylinder
with no blank space. Instead half the cylinder slides back and forth into three positions.
Thus the middle half-ring on one side may get matched with any half-ring on the other side.
I haven't found any simple processes, but I expect it will have 30! =
265 25285 98121 91058 63630 814800 00000 patterns if the pieces are all distinct. It comes
with 3 pieces of each of ten colours, so this gives 30! / 3!10 =
43867 97336 28584 44800 00000 patterns. The advertising refers to the larger number, which
is a bit unreasonable.
VIP SPHERE
This is produced by Logitoy (Switzerland) based on Petutschnig's idea. It is a sphere
with four horizontal layers with 8 pieces in each layer.
One half of the sphere turns on a vertical plane in multiples of 180°. The group is a
subgroup of the Orb-It group. Since only 180° turns occur, the top and bottom levels never
get mixed with the middle levels and the pieces are not interchangeable so this is clearly
seen. One has 16!2 = 43 77631 36697 39505 25440 00000 patterns since all 32
pieces are distinct. (It has 8 colours with gradated intensities.)
© David Singmaster
The text and original drawings are copyright © David Singmaster, reproduced here with
permission. Conversion to html and additional commentary by Jaap Scherphuis.
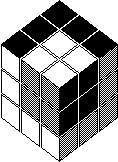
 All of the above puzzles have either blank positions or auxiliary positions. Rubik's Cube
has no such blanks, so any sequence of moves can be combined with any other sequence. Thus
the set of all patterns is the group of interest, rather than the set of patterns which
leave the blanks or auxiliaries fixed. If one considers just two or three faces of the
33, e.g. <F,R> (N55-57) or <F, U, R>, then one has two or three
interlocking 4-cycles which can be drawn on a plane as in the diagram. About a year ago, I
began to contemplate planar puzzles with this structure, but I never got very far. I
believe the analysis of sliding piece puzzles with one blank on a general graph has been
done and will appear in Winning Ways (= BCG) which has just appeared (though I haven't
seen one yet). I am not sure if this also does the interlocking cycle puzzles.
All of the above puzzles have either blank positions or auxiliary positions. Rubik's Cube
has no such blanks, so any sequence of moves can be combined with any other sequence. Thus
the set of all patterns is the group of interest, rather than the set of patterns which
leave the blanks or auxiliaries fixed. If one considers just two or three faces of the
33, e.g. <F,R> (N55-57) or <F, U, R>, then one has two or three
interlocking 4-cycles which can be drawn on a plane as in the diagram. About a year ago, I
began to contemplate planar puzzles with this structure, but I never got very far. I
believe the analysis of sliding piece puzzles with one blank on a general graph has been
done and will appear in Winning Ways (= BCG) which has just appeared (though I haven't
seen one yet). I am not sure if this also does the interlocking cycle puzzles.
 This idea is due to Endre Pap and three coworkers. The simplest version which is the
only one that has yet appeared, has two intersecting rings of 20 balls (hence 38 all
together). At the intersections, which are five balls apart, a ball can move with either
ring. The puzzle seems quite simple. The commutator of the two ring moves is a pair of
3-cycles, but it takes some time and effort to find elementary processes such as a pair
of 2-cycles, and a solution strategy. Since a ring turn is a 20-cycle, which is an odd
permutation, one can get all 38! = 52302 26174 66601 11176 00072 24100 07429 12000 00000
patterns when the pieces are distinct. The puzzle comes with 10 balls of each of two
colours and 9 balls of two other colours, so there are then
38!/(10!·10!·9!·9!) = 3 01625 69686 36903 99200
distinguishable patterns. With so many identical pieces, it is hard to keep track of the
position of a ring. I wrote a computer simulation to make it easier! There are several
suggested patterns in the instructions. The original pattern as solid coloured arcs as
shown. The most difficult has two colours alternating on each ring. Dan Sleator tells
me there is a 19th century patent on this idea, but the present exemplification has
differences which may justify a new patent. I gather that several variations with more
rings will appear. A different two ring version has been invented by Ivan Moscovitch,
the noted Israeli inventor of puzzles. Perhaps we should call this a bicycle?
This idea is due to Endre Pap and three coworkers. The simplest version which is the
only one that has yet appeared, has two intersecting rings of 20 balls (hence 38 all
together). At the intersections, which are five balls apart, a ball can move with either
ring. The puzzle seems quite simple. The commutator of the two ring moves is a pair of
3-cycles, but it takes some time and effort to find elementary processes such as a pair
of 2-cycles, and a solution strategy. Since a ring turn is a 20-cycle, which is an odd
permutation, one can get all 38! = 52302 26174 66601 11176 00072 24100 07429 12000 00000
patterns when the pieces are distinct. The puzzle comes with 10 balls of each of two
colours and 9 balls of two other colours, so there are then
38!/(10!·10!·9!·9!) = 3 01625 69686 36903 99200
distinguishable patterns. With so many identical pieces, it is hard to keep track of the
position of a ring. I wrote a computer simulation to make it easier! There are several
suggested patterns in the instructions. The original pattern as solid coloured arcs as
shown. The most difficult has two colours alternating on each ring. Dan Sleator tells
me there is a 19th century patent on this idea, but the present exemplification has
differences which may justify a new patent. I gather that several variations with more
rings will appear. A different two ring version has been invented by Ivan Moscovitch,
the noted Israeli inventor of puzzles. Perhaps we should call this a bicycle? If one thinks about planar cycles with solid pieces instead of tails, there are many
possible patterns, but the pieces start getting fiddly. Dan Sleator suggested the
following, which may be produced by Mèffert. Consider the diagram of four circles.
Each circle can rotate and this permutes the 12 'lens' pieces. The structure of commutators,
etc. are easy to see here because of the planarity and one easily gets al 12! = 4790 01600
patterns. The even valency at the centre guarantees that no orientation changes occur.
Mèffert's prototype has 6 circles in a 3 by 2 array, giving 17 pieces and 17! =
35568 74280 96000 patterns when all the pieces are distinct. But the prototype has 3 pieces
of 3 colours and 2 pieces of 4 other colours, giving
17!/(3!3·2!4) = 10 29188 16000 distinct patterns.
I am told of a game by Milton Bradley (?) called Turntables (?) which used the same
mechanism. (There is no new thing under the sun!)
If one thinks about planar cycles with solid pieces instead of tails, there are many
possible patterns, but the pieces start getting fiddly. Dan Sleator suggested the
following, which may be produced by Mèffert. Consider the diagram of four circles.
Each circle can rotate and this permutes the 12 'lens' pieces. The structure of commutators,
etc. are easy to see here because of the planarity and one easily gets al 12! = 4790 01600
patterns. The even valency at the centre guarantees that no orientation changes occur.
Mèffert's prototype has 6 circles in a 3 by 2 array, giving 17 pieces and 17! =
35568 74280 96000 patterns when all the pieces are distinct. But the prototype has 3 pieces
of 3 colours and 2 pieces of 4 other colours, giving
17!/(3!3·2!4) = 10 29188 16000 distinct patterns.
I am told of a game by Milton Bradley (?) called Turntables (?) which used the same
mechanism. (There is no new thing under the sun!)
 Rotascope is an unsymmetric approach to a triangular version of the above. Here the
pieces are not all the same, so rotation of one disc can block other rotations. The set of
patterns is not a group - one must consider just the patterns with the centre (C) and the
rims (R) fixed. Exercise 1. The rims cannot be permuted. Thus we get just permutations of
the 9 shields (S) and a counting argument shows we only ever get the even permutations of
these, i.e. 9!/2 = 1 81440 patterns. All these are achievable. Exercise 2. The shortest
process leaving the rims and centre fixed is 8 moves long. Exercise 3. The centre cannot
be twisted by itself.
Rotascope is an unsymmetric approach to a triangular version of the above. Here the
pieces are not all the same, so rotation of one disc can block other rotations. The set of
patterns is not a group - one must consider just the patterns with the centre (C) and the
rims (R) fixed. Exercise 1. The rims cannot be permuted. Thus we get just permutations of
the 9 shields (S) and a counting argument shows we only ever get the even permutations of
these, i.e. 9!/2 = 1 81440 patterns. All these are achievable. Exercise 2. The shortest
process leaving the rims and centre fixed is 8 moves long. Exercise 3. The centre cannot
be twisted by itself. This is another Hungarian production exported by Konsumex. It has three interlocking
cycles arranged as orthogonal great circles on a sphere. Each cycle has 12 square pieces,
making 30 in all. These occur in 15 antipodal pairs. The pairs can be permuted in 15! ways
and each pair can be inverted, giving 15!·215 = 42 84987 36906 24000 positional
patterns. However the square pieces have four sides which can be distinguished. By carefully
shifting a piece around three sides of a triangle, on can twist one piece. (Its antipode
twists oppositely which satisfies the conservation law.) Hence there are
15! 215·415 = 4 60097 01534 74022 5458l 76000 patterns
if the pieces and their sides are distinct. On the puzzle as a supplied, four sectors of the
sphere are coloured say with A, B, C, D, with the colour boundaries along cycles. This
gives 1 4-coloured pair, 10 2-coloured pairs, and 4 1-coloured pairs. (A 1-coloured pair
has its two pieces each 1-coloured but of different colours, etc.) The 2-coloured pairs
are of only two types: AB opposite CD and BC opposite DA. Likewise the 1-coloured pairs
are of only two types: A opposite C and B opposite D. This gives
15!/(1!·5!·5!·2!·2!) · 215·411·14 = 3120 23258 02097 04960 distinct patterns.
This is another Hungarian production exported by Konsumex. It has three interlocking
cycles arranged as orthogonal great circles on a sphere. Each cycle has 12 square pieces,
making 30 in all. These occur in 15 antipodal pairs. The pairs can be permuted in 15! ways
and each pair can be inverted, giving 15!·215 = 42 84987 36906 24000 positional
patterns. However the square pieces have four sides which can be distinguished. By carefully
shifting a piece around three sides of a triangle, on can twist one piece. (Its antipode
twists oppositely which satisfies the conservation law.) Hence there are
15! 215·415 = 4 60097 01534 74022 5458l 76000 patterns
if the pieces and their sides are distinct. On the puzzle as a supplied, four sectors of the
sphere are coloured say with A, B, C, D, with the colour boundaries along cycles. This
gives 1 4-coloured pair, 10 2-coloured pairs, and 4 1-coloured pairs. (A 1-coloured pair
has its two pieces each 1-coloured but of different colours, etc.) The 2-coloured pairs
are of only two types: AB opposite CD and BC opposite DA. Likewise the 1-coloured pairs
are of only two types: A opposite C and B opposite D. This gives
15!/(1!·5!·5!·2!·2!) · 215·411·14 = 3120 23258 02097 04960 distinct patterns.