Jaap's Puzzle Page

Nintendo Ten Billion Barrel

Nintendo Billion Barrel Nintendo Billion Star Barrel

Description of the puzzle
Notation used in the solutions
Solution 1 (columns, simple)
Solution 2 (layers)
Solution 3 (columns)

Description:

This extremely difficult puzzle was made by Nintendo in 1980 before they limited themselves to game computers. The Ten Billion Barrel is sometimes called the Billion barrel, 1010, or the Nintendo Tumbler Puzzle. It was invented by Gumpei Yokoi. A transparent star-shaped version was made recently for members of the Nintendo Club.

The puzzle has 23 coloured balls arranged in five columns spaced evenly around the sides of the barrel. The barrel itself has six rows. Two (nonadjacent) columns have only 4 balls, which lie in the middle four rows. The other three columns have 5 balls, and the extra balls either lie all in the top row or all in the bottom row. The black central core can move up or down, and that moves those three columns along with it. The middle four rows lie in two discs, which can rotate. By rotating a disc, the balls in the two rows it contains are moved around to the other columns. The aim is to place four balls of the same colour in each of the five columns, with the three black balls filling up the top of the longer columns.

Although this puzzle looks similar to the Ivory Tower, the Whip-It and the Missing Link, those puzzles have a gap so you can move pieces individually. The Nintendo barrel only allows you to move no fewer than 10 balls at a time which makes it rather difficult.

The puzzle was invented at Nintendo by Gunpei Yokoi (who also invented/designed the Gameboy). The US patent, which also covers the Trillion puzzle, was filed on 30 December 1980 and granted on 15 March 1983 (US 4,376,537 and also design patent D267,661).

In the far east it has been produced again recently. The small bit of paper supplied with it has the following amusing Japanglish text, quoted verbatim:

Cylindric Revolving Puzzler of good quality and fine appearance, provides educational value and also suit for decoration and giveaway in business. It holds colored beads in red, orange, yellow, green, blue, black etc, which present you 10 billion combinations. Cylindric Revolving Puzzler original type is laid three black bead at buttom, the second layer holds 4 same color bead in a row and spread 5 different rows arranged clockwise in the roder of blue, green, yellow, orange, red.
Mix the beads up, then here you start the game!		 It may firstly beat your brains quite a bit. Yet you may try to arrange for a row at beginning, then two, three rows to four, four rows. You will finally grasp secret from this challenge and be in enchanted with it.

If your browser supports JavaScript, then you can play the Nintendo Ten Billion Barrel by clicking the link below:

JavaScript Nintendo Ten Billion Barrel

The number of positions:

There are 23 balls which gives a maximum of 23! positions. This limit is not reached because:

This last factor comes about because it does not matter which colour goes in which column. This leaves 23! / (3!·4!5 5!) = 4,509,264,634,875 or 4.5·1012 positions. This far exceeds the 10 billion figure on the packaging.

If all the balls were different then, according to David Singmaster (in Cubic Circular Issue 2) all 23!/2 even permutations of the balls are achievable, even if the two discs are locked together. By turning the puzzle upside down, all odd permutations can also be achieved.

Links to other useful pages:

Wolfram Demonstrations Project has a Nintendo Barrel simulation.

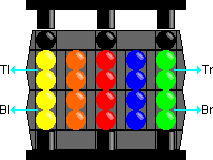
Notation:

The central core of the barrel will be assumed to be in its upwards position, the way it is when the puzzle is put down. The letters T and B will be used for moves which rotate one of the two discs, the Top or Bottom one. If the core is up, then Tl or Bl mean moving a disc one step to the left (clockwise when viewed from above), whereas two steps (i.e. 2/5 of full circle) will be shown as Tll or Bll. Similarly right turns are Tr, Br, Trr, Brr. If these same moves are performed while the centre core is pushed down, then small letters are used, e.g. tl, tll, trr, tr, and bl, bll, brr, br.

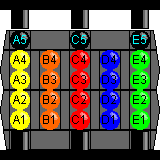As said before, normally the central core will be held in the up position. The rows are counted from the bottom up, so the bottom row is called the first row, and the top row which has only three balls is the fifth row. The puzzle is always held in such a way that the two short columns are at the front left and right. One of the three long columns is directly in front, and the two adjacent ones at the back. Lets label the columns too from A to E; the back left column is column A, the front column is C, the back right column is E. The position of each ball can then be described easily, for example C5 is the ball at the top of the front column.


Solution 1:

This is a simple solution by Pedro Luis that can be easily memorised.

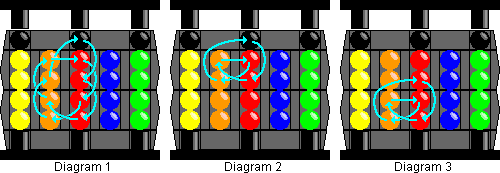This solution uses mostly just 3 very easy move sequences (and their inverses).
9-cycle: (tr br) (Tl Bl), repeated 11 times.
The 9 balls in columns B and C are cycled clockwise two steps, as shown in the diagram 1.
Top 5-cycle: tr Tl, repeated 7 times.
The 2 top balls of B and the 3 top balls of C are cycled clockwise two steps, as shown in the diagram 2.
Bottom 5-cycle: br Bl, repeated 7 times.
The 2 bottom balls of B and the 3 bottom balls of C are cycled clockwise two steps, as shown in the diagram 3.

Phase 1: Put black balls at A5 and E5.

  1. Use the move sequences above (or any other method) to bring two black balls one on top of the other in the same column (but not at A5 or E5). This can often be done intuitively, but if you can't, one sure way to do this is as follows:
    1. Put the two balls in adjacent columns, and rotate the disks so they are in columns C and D. This is always easy.
    2. Use the move sequences (e.g. the 9-cycle) to bring one black ball into position C1 (bottom of columns C).
    3. Do Tll Bll, so that one black ball is at A1, the other in column B.
    4. Use the move sequences (e.g. the 9-cycle) to put the second black ball at B1.
    5. Do Br (so the balls are at C1, D1)
    6. Do br Bl, to stack the balls up in one column.
  2. Rotate the disk(s) so that the pair of black balls lies in column D.
  3. Repeat (tr br) (Tl Bl) until the black balls are in position at A5 and E5.

Phase 2: Make column A of one colour.

  1. Choose a colour to solve first.
  2. If there is no ball of that colour in column B or C, then do the following:
    1. Do Tl Bl, shifting the columns left. There should now be at least one ball of your colour in column C.
    2. Do the 9-cycle until there is a ball of your colour in column B.
    3. Do Tr Br, shifting the columns back to the right.
  3. Repeatedly do the 9-cycle until B1 has a ball of the chosen colour.
  4. Put the ball in place at the bottom of column A as follows:
    1. Do Tr Br, shifting the columns right. The ball you are adding lies at C1, and any previously solved balls of that colour are at the bottom of column B.
    2. Do the 9-cycle five times (or its inverse 4 times) so that the ball has been inserted at the bottom of column B.
    3. Do Tl Bl, shifting the columns back to the left.
  5. Repeat steps b-d until column A is solved.

Phase 3: Solve two more columns.

  1. Do Tl Bl, so that E is the solved column.
  2. Do phase 2 again, solving column A with another colour.
  3. Do Tl Bl, so that D and E are the solved columns.
  4. Do phase 2 once more, solving column A with a third colour. This leaves only columns B and C.

Phase 4: Solve the last two columns.

  1. Choose which colour you want column B to become.
  2. Bring the four balls of that colour into the bottom two rows. The easiest way to do so is as follows:
    1. Do the Top 5-cycle until position C3 is of the chosen colour.
    2. Do the Bottom 5-cycle 3 times (or its inverse 4 times) to bring that ball downwards to C2.
    3. Repeat steps 1-2 until all balls of the chosen colour lie in the bottom two rows.
  3. Do the Top 5-cycle until the black ball lies at B3.
  4. Do the 9-cycle to put all the pieces in their correct positions.

Solution 2:

This solution will solve the Nintendo barrel row by row. It is based on the solution by James G. Nourse in "Simple Solutions to Cubic Puzzles".

In the first two phases the bottom two rows will be solved. There are a few useful sequences that move balls from row to row, without disturbing the bottom two rows. For example, tr Tl, moves C5 to C4, and C4 to C3. If you look carefully, you will see that you can use very similar sequences (that do not involve turning the bottom disc) to move any ball in rows 4 or 5 down to row 3.

One other useful move sequence is:
Double Swap: bll Tll brr (Trr).
This sequence swaps B2 and B3, and also A3 and C3. The last move in the sequence is usually not necessary because we will only use it when building the first two rows. You can use it to lift a ball from row 2 up to row 3 in column B, and vice versa, to drop a ball from row 3 to row 2. Of course, if you need to lift a ball in another column from row 2, then you can turn the bottom disc to bring it to column B, do the double swap, and return the bottom disc to its original position.

Phase 1: Solve the first (bottom) row.

  1. Consider which colours you want in each column. If you do not care which order the columns are in, and the first row already has all five different colours, then you can skip this phase completely.
  2. Turn the bottom disc so that A1 has a non-black ball. Consider that ball to be the correct colour for column A. Remember that when you have solved the puzzle, you can always move the two discs around to bring that colour to any other column anyway. Let a to e denote the colours that the columns A to E will eventually have, i.e. ball A1 already has colour a.
  3. Do Br, to bring the first ball to B1.
  4. Bring a ball of colour e to B2 as follows:
    1. Find a ball in row 3 of colour e. If there is none on row 3, then you can bring one to row 3 using the methods discussed above.
    2. Turn the top disc to bring the ball to B3.
    3. Do the double swap to bring it to B2.
  5. Do Brr, bringing the first two balls to D1 and D2.
  6. Bring a ball of colour c to B2, in the exact same way as before.
  7. Do Br bl. This puts the three balls in positions E1, D1 and B1.
  8. Bring a ball of colour b to B2, just as before.
  9. Do Bll.
  10. Bring a ball of colour d to B2, as before.
  11. Do Bll bl. The bottom row should now be correct.

Phase 2: Solve the second row.

  1. Turn the bottom row until B1 and B2 have different colours.
  2. Find a piece of the same colour as B1, and bring it to B2, using the exact same method as was used in the first phase.
  3. Repeat steps a and b until the bottom two rows are solved.

Phase 3: Solve the third row.

  1. Turn the top disc to match as many of the balls in the third row with those on the second row.
  2. Find a column where the third row has the wrong colour ball. Turn both discs to bring that column to the front, to column C.
  3. Find a ball that belongs at C3. There are 12 possible positions it could be in. Do the relevant sequence below:
    A3: tll Tll tll Trr tr Tr tll Tl tll
    B3: Tl tl Tll tll Tl trr Trr trr
    D3: Tr tr Trr trr Tr tll Tll tll
    E3: trr Trr trr Tll tl Tl trr Tr trr
    A4: tr Trr trr Trr tr Trr trr Trr tr
    B4: trr Tl tl Tll tr Tll tll
    C4: trr Tr trr Trr tr Tl trr Tr trr
    D4: tll Tr tr Trr tl Trr trr
    E4: tl Tll tll Tll tl Tll tll Tll tl
    A5: Trr tr Tll tll Tll tll Tr tr Tll
    C5: tll Tll tr Tll tl Tl trr
    E5: Tll tl Trr trr Trr trr Tl tl Trr
  4. Repeat steps b and c until the third row is correct.

Phase 4: Solve the fifth row.
Repeat the 3 steps below until all black balls are in the top row.

  1. If A5 is not black, then turn both discs so that a column containing a black ball is in column D. To move the black ball from D4 to the top row, do the sequence:
    tll Tr tr Tll tr Tr tr Tll tll
    The black ball will not necessarily go to position A5, but it will go in the top row.
  2. If C5 is not black, then turn both discs so that a column containing a black ball is in column B. To move the black ball from B4 to the top row, do the sequence:
    tll Tll tr Tr tr Tll tr Tr tll
    The black ball will not necessarily go to position C5, but it will go in the top row.
  3. If E5 is not black, then turn both discs so that a column containing a black ball is in column B. To move the black ball from B4 to the top row, do the sequence:
    trr Tl tl Trr tl Tl tl Trr trr
    The black ball will not necessarily go to position E5, but it will go in the top row.

Phase 5: Solve the fourth row.

  1. Only the fourth row is left, and this can be solved quite easily by swapping the balls around. Find two balls on the fourth row which when swapped will put at least one of them in the correct column.
  2. Turn both discs to bring the two columns to column C and one of A or B.
  3. To swap B4 and C4, do:
    trr Tl tl Trr tl brr Tl trr Trr bll Trr
    To swap A4 and C4, do:
    tr Tl Bl bll Tll brr Tll tl Br

Solution 3:

This solution will mostly solve the Nintendo barrel in columns. Most move sequences in this solution were found by computer.

Phase 1: Solve the black balls (the top row).

  1. If A5 is not black then turn the discs to bring a black ball in column A, and repeat Br Tr bl tl until it is at A5.
  2. If C5 is not black then turn the discs to bring a black ball in column C. Alternate the sequences Tr tl and Tl tr until it is at C5. Note that the first sequence moves A5 to E5, and the second moves it back again. If the first black ball ends up at E5 when C5 is solved, then do tll to prepare for the next step.
  3. If E5 is not black then turn the discs to bring it to column D. Alternate the sequences trr brr Tll Bll and tll bll Trr Brr until it is at D4. Note that the first sequence moves A5, C5 to C5, E5 and the second moves them back again. If the black balls are now at A5, C5, D4 then do trr to solve them. If on the other hand they are at C5, E5, D4 then they can be solved by Tll tll.

Phase 2: Solve the columns.

  1. Decide what colour you want each of the columns to be. Turn the discs to bring as many balls as possible into their correct columns.
  2. Find a ball that is in the wrong column. Find the column it should be, and find a ball in that column that is also wrong (preferably belonging in the first column). These two balls will be swapped.
  3. Turn both discs together so that the two balls lie in column C and column A or B.
  4. To swap the two balls, do the relevant sequence below:
    A1, C1: Bll br Tll br Trr Bl br Tll br Tr
    A2, C1: Tll Brr brr Bl bll Brr br Bll br
    A3, C1: Bl bll Bl brr Tll bll Br brr Tr
    A4, C1: tr Tll br Bl Tll br Br bl Tl tl
    B1, C1: Bl brr Br bll Br Tr bll Br brr Bl
    B2, C1: Trr Bll br Tl Bl bl Tr bll Tr bl
    B3, C1: Tll br Tll Bl br Br bl Tl
    B4, C1: Tr tr Trr br Tll Bl br Br tl bl Tl
    A1, C2: bl Trr bl Bl Tll bl Trr bl
    A2, C2: Br bl tl Tll bll Trr tr bll Bl
    A3, C2: Bl brr Tr bl Tll bl
    A4, C2: Bl tr br Tr br Tl tl bll Br
    B1, C2: Trr brr Bl bll Bl brr Bll bl Tr
    B2, C2: Bl bll Tl brr Br bll Tr brr
    B3, C2: Bll bl Br Trr bl Bl Tr br
    B4, C2: Bl Tl tr Tll bll Trr tl Tll brr Trr
    A1, C3: Br Tll bll Bl brr Trr bll Br brr Bl
    A2, C3: Bll Trr bll Tl br Trr br
    A3, C3: bll Tll brr Trr
    A4, C3: Trr tl Tll brr Trr tr bll Tll
    B1, C3: Br Tll bl Trr Br bl Bl br Bl
    B2, C3: Trr tll Trr bll Tll trr brr Tll
    B3, C3: Trr bl Trr brr Tll bl Tll
    B4, C3: Tll tl Trr bll Tll tr brr Trr
    A1, C4: Bll tl brr Tll Br bll Trr tr brr Bl bll Brr
    A2, C4: Trr Bll tl bl Tl bl Tr tr brr Bl
    A3, C4: tr Trr Brr bll Tll tl brr Bll
    A4, C4: Tl Bll tll bll Tl tll brr Tll Bll tl
    B1, C4: Br tl Tll bl Trr Br bl Bl tr br Bl
    B2, C4: tl Tll bll Trr tr Tll brr Trr
    B3, C4: Tll Br tr brr Tll bll Trr Brr tl
    B4, C4: Tl tll Tr tl Tll tl Tll tll Trr tr
    Note that these sequences will mix up each column, but only the two chosen balls will move to a different column.
  5. Repeat steps b-d until all the columns are solved.

Other sequences

  1. Column swaps: (Calculated by Mike Godfrey)
    Swap A,C: br Bl br Bl bll tr Tr brr Tl brr Bll bl tl
    Swap B,D: Tr bll tl Trr bll Bl Tll bl Tr br b1 Tl bl tr Tl
    Swap B,E: Tr br Br bl Brr bll tr Tl bl Brr Tr brr tl Brr Tl
    Swap A,B: trr Bll Tl bl Tl tll Tr trr Tll brr Br bll Trr bll Tl
    Swap B,C: Br bll Tr bll trr Tr tll Brr Tr bll Brr Tl br Tll trr Tll
    Swap A,E: tr Bl Tr bl Tl brr Br brr tll Tl bl Tr tr Bl

Pretty patterns:

  1. Spiral:
    bll Tr bll Tr bl Bl Tl br Bl
  2. Zig Zag:
    Do Spiral followed by Brr.
  3. Flag:
    bll Trr Brr tll brr Trr tl br Trr Bl tr br Tr Br brr
  4. Topsy Turvy (is similar when turned over).
    Tr tll Tr tr Tl tl Tr tr Tll