CUBIC CIRCULAR
A quarterly newsletter for Rubik Cube addicts
Issue 5 & 6
Autumn & Winter 1982
ANOTHER DOUBLE ISSUE
| CONTENTS | | | |
| Editor's Corner | | 2 | |
| More on the U Group | | 2 | |
| Cubathons | | 2 | |
| The n-Dimensional Cube Solved | | 3 | |
| Miscellany | | 4 | |
| New Cube Products | | 5 | |
| Tsukuda's Square | | 7 | |
| More Clubs | | 8 | |
| Generalized Hungarian Rings | | 9 | |
| The Incredi-Ball (or Impossiball) | | 10 | |
| Going Ape over the Cube | | 10 | |
| Some Geometric Puzzles | | | |
| A. Eight Cube Rings | | 11 | |
| B. Twelve Tetrahedra Rings | | 13 | |
| C. Cubic Snakes | | 14 | |
| Some Notes on the 43 | | 15 | |
| Pyraminx | | 18 | |
| Cubism and Religion | | 22 | |
| Prehistory of the Cube | | 23 | |
| Local Maxima | | 24 | |
| The Trials of the Cube | | 25 | |
| A Czech Check Problem | | 25 | |
| God's Algorithms | | 26 | |
| First Day Cover | | 28 | |
| Block of 4 Stamps | | 28 | |
Published by David Singmaster, 87 Rodenhurst Road, London, SW4 8AF, UK
ISBN No. 0261-8362. All material © 1982 by David Singmaster.
2
EDITOR' S CORNER
IMPORTANT NOTICE: Due to retrenchment at David Singmaster Ltd., I
am now running the Cubic Circular personally. All future correspondence
should be addressed to CUBIC CIRCULAR, 87 RODENHURST ROAD, LONDON, SW4 8AF,
UK. Subscription cheques should be made out to David Singmaster. Subscribe
now - give a gift subscription for Christmas: Subscription rate for the
second year is £4 or $8. Back issues of Volume 1 available for
£3 or $6.
From July, Peter Light has been assisting me in dealing with the mass of
accumulated correspondence. By now, almost everyone will have had some reply
to their letters - some of which are eighteen months old! We have not had
time to digest everything and there are a number of letters (e.g. in other
languages) which he has not been able to deal with. We hope everything will
be cleared away by the new year:
Let me urge correspondents to send stamped addressed envelopes (or at
least a mailing label and a reply coupon): Also, please make sure your name
and address and the date is on the contents as well as the envelope -
envelopes do get separated from their contents and contents sometimes get
filed in different ways.
Peter has also been testing the various computer programs which have been
sent in.
Some of this Circular has been typed with 1 1/2 spacing instead of single
spacing. This gives about 25% fever lines per page but is more readable.
What do you think?
I would be delighted to receive contributions in the form of short
articles for the Circular.
On page 3, I mention the Rubik's Cube stamps from Hungary. I have
arranged to print these on the back page and the following has been
transferred from there to make room for it.
MORE ON THE U GROUP (N49, C3/4-17,36)
Nicolas Hammond has a method for the U group in at most 21 moves.
J.F. Jarvis (96 Forrest Ave., Fair Haven, New Jersey, 07701, USA) has
an inventory of U processes and would like to hear from anyone interested
in compiling a directory with him. (Mr. Jarvis, meet Mr. Hammond - Mr,
Hammond, meet Mr. Jarvis!)
CUBATHONS
In the 24 hour Cubathon of PCs Timoney and Pullen (C3/4-7), they
completed 1043 Cubes in 24 hours. That's 21.73 cubes per man-hour, or an
average of 2.76 min or 2 min 45.7 sec per cube.
Cardiff Students Rag 1982 had a Cubathon in which two students solved
2000 Cubes in 36 hours. That's 27.78 cubes per man-hour or an average of
2.16 min or 2 min 9.6 sec per cube.
3
The n-DIMENSIONAL CUBE SOLVED
Joe Buhler, Brad (3D) Jackson and Dave Sibley have drafted their work on
the n-dimensional Rubik Cube. Like Keane and Kamack (C2-8), they allow
orientation preserving movements of the n-1 dimensional facets of the n
cube. The constructible group is a direct product of the appropriate wreath
products
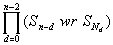
where Nd = 2n-d n! / d!(n-d)! is the number of
d-dimensional faces of an n-cube, but when d = 0, we take An-d
instead of Sn-d. They find several conversation laws which yield
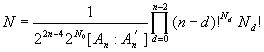
Where [An:An'] = 3 for n=3, 4 and is otherwise 1.
It is not clear how the expression works for n=2.
4
MISCELLANY
Several readers have been confused by expressions involving commutators.
Recall that (N30,41) [A,B] = ABA'B'. Hence
[A,B]-1 = (ABA'B')-1 = BAB'A' = [B,A]!! Thus we have
[A,[B,C]] = A·[B,C]·A'·[B,C]'
= A·[B,C]·A'·[C,B] = A·BCB'C'·A'·CBC'B', and
[A,[B,C]]' = [[B,C],A] = [B,C]·A·[C,B]·A' = BCB'C'·ACBC'B'·A'.
I forgot to mention that the First World Championship in Budapest was
commemorated by a special 2-forint stamp, with First Day Covers, etc. If
space and reproduction permit, I'll try to include a picture on the back
page.
Several readers assert that WD40 and other aerosol spray lubricants can
dissolve the central spindle!
The handbook of Cubik Math, by A. H. (Sandy) Frey and myself, is now
available in the UK and Europe from Lutterworth Press. The UK list price
is £5.95. I will be happy to dispatch copies to the UK and Europe
for $6.50, including post and packing. The book has been well reviewed.
"A book that will delight enthusiasts"
"The solution in Chapter 3 is ... intelligent and breathtaking in its
simplicity."
An article in Science 82 reports a 19 year old autistic child who
doesn't speak but solved his first cube in 40 seconds!
An Auckland (New Zealand) paper reported a solution time of 5.51 seconds!
A French engineer, Alex Renault, at the firm AKR, has built a 'Rubik Robot
with video colour detector which takes about 15 seconds per turn.
A cubical question was set on a UK entrance exam: "Exam Paper for Awards
and Entrances in the College of the University of Cambridge - Paper 871,
Physics & Maths, 23 Nov 1981". Question 12 asks how many ways one can
reassemble a cube when cut into 27 cubies and one wants the colours outside,
and what is the probability of getting the U face all blue.
Arthur P. Cracknell reports that the Cube proved an exception to a well
known scientific law. The law is that no-one comes to lectures on the last
afternoon of a conference. The exception was a lecture by Hans Zassenhaus
at a colloquium on group theoretic methods in physics at the University of
Kent, which was the last and most attended lecture of the colloquium.
At C2-4, I reported that 3 year old Glenn Quackenbush could do the Cube.
His father writes that he can 'only' do several patterns - still that's not
bad for a 3 year old.
5
NEW CUBE PRODUCTS
I have been kindly sent cubes with five fruits and Chex (a US cereal box
top offer) and with Pac Man symbols. Several full-face patterns have
appeared: animals, butterflies, copulating couples: In Italy, I found
several interesting Ideas: Football Cubo - with full-face colours of six
leading football (= soccer) clubs; Caricatur Cubo - with full-face
caricatures of six Italian political party leaders; Italian Political Cube -
with symbols of the six major parties (It can't get any more confused than
Italian politics. Perhaps it's used for predicting Italian election results!);
Souvenir di Venezia - with five full Venetian scenes and the motto on the
sixth face. (I saw a ample of a scenic cube in Nuremberg, but this is the
first I've seen on sale.) Neil C. Rubenking sends a cube with four colours
forming pyramids about four alternate corners. He also sends a slightly
melted cube, transfixed by a large brass screw, mounted on a wood base with
a brass plate: "SCREW IT". In Holland, the all black cube
(C3/4-10) is called the Belgian Cube.
The unnamed shape mentioned on C3/4-11 is
a truncated rhombic dodecahedron. I have examined a Taiwanese 23
(C3/4-9) and its mechanism is similar to Rubik's
23 patent. That is, it is a 33 with its corners
concealing the edges and centres. It differs from Rubik's method in details,
but it is still a very complex design.
Jorg Brown, age 13, of Fort Collins, Colorado, has designed (but not
built) a 53.
Edward Hordern has made a 33 into a 43 by gluing
extra pieces on 3 sides. This causes the 42 faces to rotate
eccentrically about one of the centre pieces. It is quite difficult to get
back into shape!
Cube Mates (Cinderella Co., P C Box 265, Sykesville, Maryland, 21784, USA)
is a set of 54 lettered stickers to put on your cube to play word games.
Every letter and * (a wild card) occurs at least once and the following more
often - 2 times: D, G, H, P, S; 3 times: B, E, R, T; 4 times: I, L, O; 6
times: A. The instructions describe several games.
Ideal has produced a Puzzle Poster in the US showing about 2,000 cubes -
one of which is wrong: They are also marketing a Jigsaw with all the pieces
the same shape, but which assemble into a pattern in just one way: (cf.
C3/4-11)
The second issue of their Rubik's Cube Newsletter has appeared. I
haven't yet seen the second issue of Rubik's (the Hungarian magazine), but
I have just heard of it.
Cubical shoelaces have come from the USA. Solomon W. Golomb sports
seeing cubical duvet covers in Amsterdam.
Although I have not yet seen examples, Mèffert has offered to send
a catalogue of his products and to supply them by mail order. His address is
Pricewell (Far East) Ltd., P.O. Box 31008, Causeway Bay, Hong Kong. The
October issue of Omni shows a Magic Dodecahedron, called Megaminx
(C3/4-19), a Pyraminx Cube (C3/4 - 12/13), and the Impossi-Ball (also called
Incredi-Ball and described elsewhere in this issue). Some other products
are mentioned. The offer to supply was made to Omni readers.
6
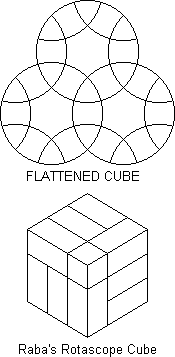 An article in La Recherche last December is partly by Raoul Raba inventor
of the Rotascope (C2-14/15).
Several variants are described. The flattened
cube is three rings which behave like three faces of a cube - but each face
has six corners and six edges. (A two-ring version of this was devised by
Doug Engel of Colorado).
An article in La Recherche last December is partly by Raoul Raba inventor
of the Rotascope (C2-14/15).
Several variants are described. The flattened
cube is three rings which behave like three faces of a cube - but each face
has six corners and six edges. (A two-ring version of this was devised by
Doug Engel of Colorado).
Two spherical versions are shown, along with
cubical equivalents. These look very like Durham's Pyraminx Cube
(C3/4-12/13),
but it's not clear just how they move. Raba also shows that the
Rotascope can be viewed as a cube with some pieces glued together as shown.
Ruth Roufberg has tracked down the earlier version of these puzzles
(C2-14/15).
It was a 1971 Parker Brothers game called Orion with a 52
array of rotating discs, each containing lenses (as on
C2-14)
Linear Aesthetic Systems, P O Box 23, West Cornwall, Connecticut, 06796,
USA, have programs to display and simulate cubes up through 73.
Diane Turnbull reports seeing a 'Cubies' chair at Heal's (Tottenham Court
Road, London). It has a plastic frame which holds small coloured cubes which
you can take out and rearrange.
Van C. Wedgwood sends his "The Idiot's solution to the Rubiks Cube" which
consists of a set of coloured labels. It costs $2.00 from PO Box 9261,
Denver, Colorado, 80221, USA. (This reminds me of what someone called the
'chemical solution' to the Cube - use some solvent to dissolve the glue of
the sticky labels and then reglue them!)
Early reports from Russia and China regarded the Cube as a symbol of
Western decadence. Izvestia reporter Melor Sturua said: "Some assert that
the Rubik Cube reflects the philosophy of the Reagan Administration - to
build and destroy aimlessly in a futile search for a solution to the world
situation. Others see Americans' efforts to solve the puzzle as the desire
to escape from a disordered life." A report from China criticised be Cube
as a time-waster and said that a boy had allowed a batch of buns to burn
in the oven while he was distracted by a Cube.
However, a more recent report in Trud reveals that the Russians have
succumbed to Cubitis. They will produce their own products -the Muldavian
Pyramid and the Nikitin Cube - early next year!
7
TSUKUDA'S SQUARE
I mentioned this briefly at
C2-9. I have had a chance to study Edward
Hordern's example and I can describe it in more detail.
My previous description was incorrect due to having seen it only briefly
and in conjunction with a Crossover.
The puzzle is a 42 board with pieces numbered 1 to 16. Each
horizontal row can be slid one place to the right, bringing in an empty
space on the left and concealing the piece on the right as In Figure 1
which shows the effect of sliding row 2. The three columns on the right
can be slid down together by one place as shown in Figure 2.
All the slides are spring loaded to return to the original positions.
Let us denote the right slide of row n by n, its left slide by n', the down
slide of columns 2, 3, 4 by V (for vertical and its up slide by V'. When V
has been made, row 1 is obstructed and slides 1 and 1' cannot be made.
8
As with other sliding piece puzzles, we have two levels of group
structure. If we include 8 extra pieces along the bottom and right edges,
we can view each move as a 5-cycle on this set of 24 pieces but the set of
patterns is not a group. We get a group structure on the 16 numbered pieces
by considering the patterns in which each extra piece is restored, i.e. each
slide is returned to its initial position. Since this requires an even number
of moves for each slide, each such pattern is an even permutation of the 16
pieces. A sequence of moves is in the group if and only if:
- it has as many 1's as 1s, ..., V's as Vs;
- the 1s and 1's, ..., alternate, in this order, in the sequence;
- 1 and 1' do not occur when there is an uncancelled V.
Commutators of moves are obvious processes with these properties, but
they are messy. To investigate them, I wrote a simulation program on my
Sinclair ZX81. This yields the following:
[2,V] = 2V2'V' = (2, 5, 6, 7, 8, 4, 3)
[23,V] = 23V2'3'V' = (2, 5, 9, 10, 11, 12, 8, 4, 3) etc. (Note
that 2'3' = 3'2'.) and
[1,[2,V]] = (1, 2) (4,8)
The last result was not quite expected since 1 and [2,V] overlap in 3
places. But 1 sends
1 → 2 → 3 → 4 →
and [2,V] sends
→ 8 → 4 → 3 → 2 → 5
so some of the interaction cancels in the middle, leaving only the 2
2-cycles at the ends of the overlap. In fact, this always happens when we
take a commutator of two cycles that overlap in a sequence of positions.
From (1,2)(4,8), it is easy to obtain (4, 8, 12) and (3, 4, 8). It is
easy to put whatever pieces are desired into locations 1 and 2. Then it is
easy to get any piece in rows 2, 3, 4 into position 8 without affecting
row 1. Thus we can achieve all the 3-cycles (3, 4, n) , n > 4, and so we
can get any even permutation of the 16 pieces.
Added in Press. This puzzle is being distributed in the UK as "It".
MORE CLUBS (Cont. from C1-12)
The Nederlanse Kubisten Club (NKC) has been established by Anneke Treep
and others (address in C2-3).
There is a Hungarian Rubik Cube Club with rooms in the Kossuth Club,
Budapest.
Georges Helm has founded the Rubik's Cube Club Luxemburg at 76 Bomecht,
L-4936 Bascharage, Luxemburg.
9
GENERALIZED HUNGARIAN RINGS
The Hungarian Rings, described at C2-14, have a nice generalisation.
Suppose we have left and right rings with m and n balls with the intersection
being a and b balls apart on these rings. Then there are N = m + n - 2 balls
all together and we consider them as all distinct. Let G(m, n, a, b) be the
group of achievable positions. Let L, R denote clockwise rotations of the
left (right) ring. Philippe Paclet [Jeux et Stratégie 16 (Aug-Sep 82)
30-32] asserted that G(m, n, a, b) always contains AN the group
of all even permutations of the N balls.
I have shown that this is not true. There is an infinite class of
exceptions and one special case.
I. G(4, 4, 1, 1) is the same as the cube group <F,R> acting on the
6 corners it affects. In N55/57, this group is discussed and shown to be
isomorphic to S5 - the group of permutations of 5 objects.
II. G(2a, 2b, a, b) is the antipodal case. Here the balls fall
into antipodal pairs which cannot be separated. There are N/2 = a + b - 1
antipodal pairs and we can view the rings as an a-cycle and a b-cycle of
these pairs. Thus it is easy to get any even permutation of pairs. Pairs
may also be inverted, e.g. [La, R] inverts two pairs.
We can view G as a group of actions on the set of a + b - 1 oriented
pairs, i.e. as a subgroup of the wreath product Z2 wr
Sa+b-1
- If a and b are odd, we get only even permutations of pairs. But
La inverts an odd number of pairs, so any number can be inverted.
So G = Z2 wr Aa+b-1.
- If a and b are of opposite parity, we get G = Z2 wr
Sa+b-1.
- If a and b are both even, we can only invert an even number pairs. The
easiest method is to use Rowley's proof (N3/4-21). Both L and R are odd
permutations of pairs and are odd permutations of the individual pieces.
So if all pairs are in place, only an even number of them can be inverted.
Hence G is the subgroup of Z2 wr Sa+b-1 in which the
parity of orientation changes is the same as the parity of the permutation
of pairs
Cases A and C give 2a+b-1 (a+b-1)!/2 patterns. Case B gives
2a+b-1 (a+b-1)!. In all cases other than mentioned in I and II,
does contain AN and = SN if m or n is even;
= AN otherwise.
In case you haven't yet solved your Hungarian Rings, here' s hint.
Consider [La,Rb], which is
[L5, R5] in the commercial version. This is equivalent
to [F, R] on corners of a cube.
10
The argument used in Case II-C above shows that I was wrong in C2-15 in
asserting that each antipodal pair on the Equator could be inverted. Thus
there are 15! 215/2 = 21 42493 68453 12000 permutations of the
pieces, 15! 215 415/2 = 2 30048 50767 37011 27290 88000
patterns when all four orientations of each pair are distinct. (Pentangle is
now importing a version with a map of the world on it which has this many
patterns.) The number of patterns on the Equator is half the number at
C2-15, line -6, namely 1560 11629 01048 52480.
THE INCREDI-BALL (or ImpossiBall)
This is described in Scientific American (July 1982) and Omni (October
1982). It consists of 20 spherical triangles (i.e. a spherical icosahedron)
with a springy mechanism which allows a 'face' of five triangles about a
vertex to rotate. There are coloured circles about each vertex. A little
thought shows the triangles are equivalent to the corners of a Magic
Dodecahedron, so there are
20!/2 320/3 /60 = 2 35639 02142 42189 66794 24000 distinct
positions where the denominator of 60 corresponds to the dodecahedron
having no centres. (Compare with C3/4-20.)
One version of the Incredi-Ball uses only six colours, like Alexander's
Star. The fact that each triangle has three colours completely fixes the
relationship of the colours, so the last discussion on C3/4-20 does not
apply. But the ten pairs of antipodal pieces can be evenly exchanged in
210/2 ways, giving
(20!/2)·(320/3) / (210/2 · 60) = 460 23246 37191
77669 52000 distinguishable patterns.
It is also possible to remove one piece and have an icosahedral sliding
piece puzzle.
GOING APE OVER THE CUBE
UK TV viewers will be familiar with the Brooke Bond tea advertisements
featuring chimpanzees who pour tea, ride bicycles, move pianos, etc.
Researchers into behaviour wondered if there was any instinctual component
in playing with the cube and so gave some cubes to the chimps. Five year
old Louis, the bicycle rider, mixed up his cube and then twiddled aimlessly
and bemusedly. Four year old Jill was fascinated by the red squares, but
then got angry with the cube and tried to eat it. The baby chimp, Charlotte
took hers apart. The chimps' owner, Molly Badnam, reported "The chimps were
clearly enthralled, playing with the cubes for long periods each day.
However, I regret to say that they showed no promise and only became more
and more exasperated. For the sake of their health, I was forced to abandon
the experiment". Sounds terribly human!
11
SOME GEOMETRIC PUZZLES
A. EIGHT CUBE RINGS
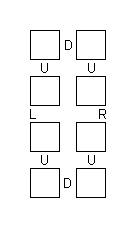 Over the years there have been a number of 'fiddlies' based on hinging
together 8 cubes along edges so that they will fold into a 23.
The best known of these has its 8 cubes joined in a ring as shown in the
diagram. The cubes are shown from above. Some of the vertical faces where
cubes meet have hinges joining their edges as indicated by the letters. When
the front and back pairs of cubes are folded up, we have a 23.
The folding can be continued through three more steps to give another
23. But then all the cubes are inverted so their previous
outsides are inside and vice versa This fiddly has been known long enough
that origamists can make the whole thing from a single strip of paper.
(There are also a number of other hingings. If the R and L are changed to L
and R and the back D is changed to B and the front D is changed to F, the
result can be folded into a cube in four ways with a tricky move required
to get between two sets of two ways.)
Over the years there have been a number of 'fiddlies' based on hinging
together 8 cubes along edges so that they will fold into a 23.
The best known of these has its 8 cubes joined in a ring as shown in the
diagram. The cubes are shown from above. Some of the vertical faces where
cubes meet have hinges joining their edges as indicated by the letters. When
the front and back pairs of cubes are folded up, we have a 23.
The folding can be continued through three more steps to give another
23. But then all the cubes are inverted so their previous
outsides are inside and vice versa This fiddly has been known long enough
that origamists can make the whole thing from a single strip of paper.
(There are also a number of other hingings. If the R and L are changed to L
and R and the back D is changed to B and the front D is changed to F, the
result can be folded into a cube in four ways with a tricky move required
to get between two sets of two ways.)
This year, a variation of the first idea above has been a popular seller
'under the name of The Shinsei Mystery (or Twin Comet) in England. Each of
the eight cubes is split into two congruent halves, with the halves meeting
along the hinged edges. Each half is separately hinged. The result is two
rings of 8 half-cubes. When joined the two rings fold together and lock like
an 8-cube ring But the two rings can be separated and each ring folds in the
same way. Each ring can be folded into an interior form and an exterior form,
both with cubical symmetry. The exterior form is a cube with an interior hole
congruent to the interior form. (Added later: It is called Starburst in the
US.)
Manufacturers assert that the idea is due to Naoki Yoshimoto, a Japanese
artist. I have found it depicted in two Japanese books, attributed to
Yoshimoto and giving a date of 1972. However the idea is
12
shown in eight forms in a 1973 article "Flexicubes - Reversible Cube
Shapes" by the Dutch puzzle inventor Jan Slothouber (J. Recreational Math.
6:l (Winter 1973) 39-46). He gives several examples where the two halves are
not congruent, giving rise to some interesting shapes.
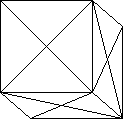
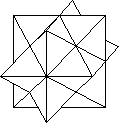 The halving used by Yoshimoto is also given by Slothouber. Consider the
cube divided into 6 square pyramids, based on the faces with the apices at
the cube centre. Three of these meeting at a corner are a half-cube congruent
to the other half. The interior form is a star-like solid which rejoices in
the name of the stellated rhombic dodecahedron. Each point of the star is a
rhombic pyramid on a face of the rhombic dodecahedron. The shape is fairly
well known because a popular assembly puzzle forms this shape from 6 pieces.
(There are two versions - one with different pieces, including a key piece
and the other with 6 identical pieces which is more interesting.)
The halving used by Yoshimoto is also given by Slothouber. Consider the
cube divided into 6 square pyramids, based on the faces with the apices at
the cube centre. Three of these meeting at a corner are a half-cube congruent
to the other half. The interior form is a star-like solid which rejoices in
the name of the stellated rhombic dodecahedron. Each point of the star is a
rhombic pyramid on a face of the rhombic dodecahedron. The shape is fairly
well known because a popular assembly puzzle forms this shape from 6 pieces.
(There are two versions - one with different pieces, including a key piece
and the other with 6 identical pieces which is more interesting.)
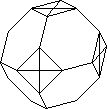
Slothouber gives two other divisions into congruent halves.
1. Imagine each cube again cut into a 23 and take 4 of the
small cubes comprising a 'pyramid' at a corner. 2 Cut each cube in half by
a plane perpendicular to a main diagonal. The interior forms of these are
shown in the figure. The second is a truncated octahedron - though Slothouber
calls it a cuboctahedron.
An amusing sidelight is that an early Taiwanese copier of the Shinsei
Mystery clearly misunderstood the idea and produced a version with only one
of the of the rings of half-cubes, thereby losing 50% of the interest of the
object. (The truncated octahedral form was independently devised in New York
last year. I've unfortunately mislaid my notes, but I believe that It was
done by two people, one of whom is Alton Bader. The first form is in
production by the Japanese Asahi Corp. (and several Taiwanese firms).
13
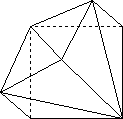
B. TWELVE TETRAHEDRA RINGS
If one divides one of the six face-based pyramids of a cube in half by a
diagonal plane through the apex and two diagonal corners of the base, then
we get two tetrahedra which are mirror images. These can be hinged in various
ways to make a ring of 12 tetrahedra which flexes on various ways.
Bart Phillips makes an elegant wooden version called "Flexicube", which
allows you to invert the six pyramids, making an exterior form which is a
rhombic dodecahedron with a cubical hole inside, the size of the original
cube. There is no way to put another cube in the interior and make them
flex together.
One can view the cuts of the six pyramids as made by three diagonal
planes of the cube which meet at a corner. The result is symmetric about
the main diagonal of the cube through this corner. Six of the hinges are
on this diagonal and six are along cube edges, forming a skew hexagon.
A second version of this fiddly, called Kaleido Puzzle or Kaleidoform,
was sent from Taiwan. It is also available as a Corgi toy and via other
importers. It has the same pieces in the same arrangement, but the hinges
are all along the cube edges. It is trickier to flex and it took me some
tome to realise that it could be inverted into a rhombic dodecahedron. It
makes a lot of patterns including half a solid rhombic dodecahedron. I have
only one copy of the ring but one version comes with two rings. One can
combine two so they will flex together but only in a limited way and not
like the Shinsei Mystery. I don't know if any hinging will allow the two
rings to flex together through an inversion.
A third variation of this idea, called the Shinsei Miracle, starts by
cutting each of the 6 face-based pyramids in quarters. This is the same
as cutting the cube by all six diagonal planes as shown. These are divided
into two congruent groups of twelve which are hinged alternately along cube
edges and along midlines (i.e. lines from a face centre through the cube
centre). Each half makes some nice shapes and there are some ways to make
the two rings flex together but they don't have the interaction of the
Mystery. It is possible to use both rings to make a rhombic dodecahedron
with a cubical hole.
14
C. CUBIC SNAKES
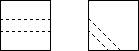 About two years ago, Diane Turnbull brought me an example of a 'folding
cube'. It consists of 27 cubes strung together with elastic. The cubes have
holes which go from a face centre to a face centre, either directly opposite
a straight piece) or adjacent (a bend piece) as shown. The object is to fold
it into a cube. For a particular arrangement of straight and bend pieces it
takes about half an hour to check all possibilities. The example brought to
me has only one solution as a 33 and no solution as a 3 × 9
rectangle. It struck me that it might be possible to have all bend pieces.
However, I have shown that one must have at least two and at most eleven
straights among the 25 interior pieces. (The end pieces cannot be classified
as straight or bend since the string doesn't continue.)
About two years ago, Diane Turnbull brought me an example of a 'folding
cube'. It consists of 27 cubes strung together with elastic. The cubes have
holes which go from a face centre to a face centre, either directly opposite
a straight piece) or adjacent (a bend piece) as shown. The object is to fold
it into a cube. For a particular arrangement of straight and bend pieces it
takes about half an hour to check all possibilities. The example brought to
me has only one solution as a 33 and no solution as a 3 × 9
rectangle. It struck me that it might be possible to have all bend pieces.
However, I have shown that one must have at least two and at most eleven
straights among the 25 interior pieces. (The end pieces cannot be classified
as straight or bend since the string doesn't continue.)
This led me to consider making other versions of the puzzle. I've
recently thought that a good name for these would be "cubic snakes". One way
to make your own is to use Multilink blocks which are plastic cubes with one
circular projection and five circular holes on the faces. These snap together
and rotate, but do not hold together well. At Nuremberg, in February, I saw
a better version of the idea developed by Antal Kelle for General Impex.
This had a more sophisticated snap mechanism with two states: loose (for
turning) and firm. I don't know if it is being produced.
This year, I have also seen three elastic versions made for Jeux
Descartes, the French puzzle distributors. These have 36, 64 and 125 pieces,
the first two being formed in a ring. All pieces are bends. Forming the 36
into a 3 × 3 × 4 is a bit tricky. I haven't yet made the 125 into a 5 - it
looks like it will take some time!
Exercise. Find all the circuits through the 27 cells of a
33. Classify them by the sequence of straight and bend pieces.
Are there any sequences which form a cube in many different ways?
15
SOME NOTES ON THE 43
A Strategy for the 43
- Do two opposite face centres, say L and R.
- Pair up and place the F, D, B edge pairs on the L and R faces.
- Put D corners in place. (Perhaps combine steps 2 and 3.)
- Pair up FD edges and store in UR, say. Pair up BD edges. Put FD and BD
edge pairs in place.
- Check the parity of the U corners. If in odd parity, apply U.
- Use the moves like [[R,U], l'] = (URb, UBl, FUl) to 3-cycle U edges to
get UR and UL edge pairs correct.
- Examine (carefully!) the parity of the four edge pieces at UF and UB. If
in odd parity, apply r2D2l'D2r2,
which 4-cycles these edges (and moves some F, U, B centres). (Since the D
centres are not affected by this or later moves, one can try to get some
(or all) D centres correct at step 4.)
- Use the moves of step 6 to get all edge pieces together.
- If you've done the parity at step 7 correctly, you may have to flip an
even number of edge pairs, which can be done as on the 3 × 3 × 3. If you find
you have to flip an odd number of pairs, you didn't examine the parity closely enough. Flipping a single edge pair requires exchanging them, which is an odd permutation. Return to step 7 if you need to do this.
- Place the U corners by use of 3 × 3 × 3 moves.
- Use moves like [[r, b], U] =(Fur, Ubr, Ubl) to 3-cycle centres into
place.
Useful moves
The trickiest step in restoring the 43 is getting the edges
into correct parity, as done in step 7 (cf. step 9). Because this requires
making a slice move, I put off getting the other centres correct until after
this step.
It is possible to exchange a single pair of edges as follows:
r2D2l'D2r2 ·
r2D'R2 · [[R, U], l'] · R2Dr2
= r2D2l'DR'UR'U'l'URU'lRDr2
= (UBl,UBr)(Ful,Ubl,Bdl,Ufr)(Fdl,Ufl,Bul,Ubr)
Jeffrey Adams' book gives
l2D2[u, F'] D2l2·LUL'u'LU'L'
= (UFl,FUr) times a 6-cycle and a 4-cycle of centres on four faces, The
centres are not as easy to correct as in my version.
Applying r2U2r (u2r2l2)2
r'U2r2 will correct the F and B centres in my process,
leaving a 180° rotation of U centres, which can be corrected by a standard
33 supergroup move.
You may find it convenient to have a 2-cycle of edge pairs.
r2D2l2D2r2 = (UFl,
UBr) (UFr, UBl) (Ufl, Ubr) (Ufr, Ubl) (Ful, Bdl) (Fdl, Bul).
Applying r2U2r (l2u2d2)2
r'U2r2 corrects all the centres.
Other strategies
After writing the above, I decided it was time to study other methods. I
mentioned Jeffrey Adams' book, called "How to Solve Rubik's Revenge" which I
have only seen briefly. He uses the same notation that I use - describing it
as a natural extension of my 33 notation. I didn't have time to
work through his method, but he does all corners, then U edges, M edges, D
edges and then centres.
16
Jerome Jean-Charles' "Solving Rubik's Revenge" aims to be suitable even
for those who haven't yet done the 33. The notation is minimal
and the directions of moves are not consistent. But he presents everything
in pictures, so the notation is not important.
Jean-Charles' strategy is as follows.
- Put all corners in place.
- Use standard edge moves to place 6 U edges in 3 U edge pairs and then
all D edges. (The missing U edges serve as 'parking places'.
- Place last U edges.
(Here he uses F'u'Fu'F'u2F = (FRu, Ufr, BLu, RBu, LFu) +
movement of centres. This is actually a 33 move. If necessary
he flips the pair after getting them in place by Fu'dF'u'dF'u'dF, though
many other 33 moves could be used.)
- Place u edges. (This uses fairly easy moves.)
- Place d edges. (Here his 'magic move' is
R'dR'F2Rd'R'F2R2d' = (FRd, Lfd) (Fur,
Bdr, Rfd, Fdl) (Ful, Bdl, Rbd, Frd).
- Place centres. (As in my Step 11.)
The key to the simplicity of Jean-Charles' strategy is that step 1 solves
the corner parity and step 4 makes the edge parity correct (at the end).
Leaving all centres till last gives a lot of freedom to move the edges. I
suspect one could adapt the strategy to place some centres at the beginning.
Michael Mrowka and Wolfgang J. Weber do the whole D face, then U corners, U
edges, M edges, centres. (More strategies in a later issue.)
Evisceration
Peter Lees has pointed out a duality which I have studied in the different
context of Noughts and Crosses (= Tic Tac Toe) on the 44 board. In
our notation, this has a very simple form: exchange upper and lower case
letters throughout an expression. Thus the dual of the corner URF is an
invisible central piece urf and the dual of the edge URf is the centre Fur.
This mapping arises in Noughts and Crosses because it reserves all the lines
of four in a row.) It turns the 43 inside out - hence the name
'evisceration'. The dual of the move R is r.
Then we have a Principle of Duality: The dual of a sequence of
moves has the same effect on the dual pieces.
This allows us to transfer knowledge from 33 moves to
43 moves as illustrated by the following. On the 33,
(F2R2)3 = (FU, FD) (RU, RD).
On the 43, (F2R2)3 = (FUl, FDr) (FUr, FDl) (RUf, RDb) (RUb, RDf) (Ful, Fdr) (Fur, Fdl) (Ruf, Rdf) (Rub, Rdf)
Let a 'column' be an intersection of two planes or layers, such as the Fl
column. Then (F2R2)3 is a pair of exchanges
of columns: (Fl, Fr) (Rf, Rb) where the columns get inverted. Thus
(f2r2)3 = (fuL, fdR) (fuR, fdL) (ruF,
rdB) (ruB, rdF) (fUL, fDR) (fUR, fDL) (rUF, rDB) (rUB, rDF) which is a pair
of exchanges of columns: (fL, fR) (rF, rB).
17
Processes which affect corner columns on the 33 lead to dual
processes which affect central columns on the 43. E.g.
U2R2L2U2R2L2
exchanges corner columns (UR, UL) (DR, DL) on the 33, so
u2r212u2r2l2
exchanges central columns (ur, ul) (dr, dl), which gives a 2-spot pattern!
The presence of the 2-spot means we can create many of the impossible
33 patterns on the 43.
Another useful process shown to me by Trevor Hutton, is based on the
33 process (F2R2)2 which is a
3-cycle of corner columns: (FL, FR, BR), so the 43 process
(f2r2)2 is a 3-cycle of central columns
(fl, fr, br). Two of these yield the 2-spot by
(r2u2)2
(b2r2)2.
Note that the part of a 33 process which affects corners
vanishes in the 43 dual process. We can also use duality in just
one or two directions, especially if we are looking at square moves. With
non-square moves, it doesn't work! - compare [F,R] with [F,r].
Special Subgroups
Many patterns have already come in the post, but here I will only mention
some special subgroups with patterns.
If we only make moves like Rr (=R2 say?), we obviously are
simulating a 23. Less obviously, moves like Rl' (=Ri
for interleaved?) also simulate 23, but in 8 copies! The squared
interleaved moves generate a number of elegant patterns of stripes and bars,
notably Ri2Fi2Ui2Ri2
which has 6 orthogonal 4-stripe patterns.
If we only make face moves, we are simulating a 33 with fat
slices. But since we can produce a single exchange of centres and of edge
pairs and we can invert a single edge pair, we can construct all the
impossible 33 patterns except those involving a twist of a single
corner. Also, we can obtain any permutation of the centres, though only 24
of these have the colours in the correct relationship.
God's Algorithm on the 43
There are 44 = 256 possible moves along an axis, e.g.
LalbrcRd where 0 <= a,
b, c, d <= 4. These include four cases where a = b = c = d. If we hold
one layer fixed, say L, then we have 64 moves, including I. It is not yet
clear just many 'moves' a move takes. For example, r really requires two
hand moves - Rr followed by R' - while Rr and even Rrl' could be counted as
a single move. The number of positions achievable after n axial moves is at
most
Tn = 1 + 192 + l92·128 + ... + 192·128n-1 =
(192·128n - 65) / 127.
This exceeds the N on C3/4-15, namely 7.4 × 1045, when
n = 22. Guessing about two hand turns or three quarter turns per axial move,
this gives about 44 hand moves or 66 quarter turns as a minimum for God's
Algorithm.
18
PYRAMINX
Several writers have sent letters on the Pyraminx. Most have pointed out
that the method in Werneck's book is not very efficient and that the English
edition did not include the pictures of Mèffert and the production
line mentioned in C1-11, nor the material on other puzzles in the German.
|
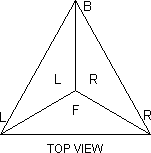
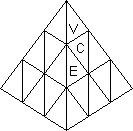
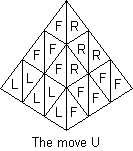
Notation. Consider the Pyraminx on a table with a face toward you.
The four corners are denoted L, R, B, U and the four faces are denoted F, R,
L, D as shown in the top view. Vertex pieces (V in the diagram) are denoted
l, r, b, u and corner pieces (C in the diagram) are denoted L, R, B, U.
Edge pieces (E in the diagram) are denoted by pairs of faces, thus: FR,
RL, LF, FD, RD, LD. Moves will be considered as rotations of a corner with
its associated vertex and edges. E.g. the move U is shown in the diagram.
Its cycle representation will be written (FR, LF, RL) Uu where U means a
120° clockwise twist of the U corner and U' will denote its opposite,
etc. (Kersten Meier uses F, R, L, U for his corners - i.e. he looks at an
edge rather than at a face.)
Solutions. For me, the simplest solution is to restore the vertices
and corners and then use:
(FR,RD,DL) = RBR'B' = [R,B];
(FR,RD BR) = RB'R'B = [R,B'];
FR+RB+ = [R,B'] [U' ,B];
to restore and flip edges.
Several solutions and many patterns have been sent in. Thanks to James
Allwright, Angus Lavery, Lawrence Cuthbert, Bill McKeeman, Martin Milner,
and Tino and Daniel Delbourgo (ages 10 and 12). David Peter has an easy
algorithm in at most 37 moves and a fast algorithm in at most 28 moves,
available from him at 50p at Wentworth College, University of York, York
YO1 5DD, UK. Another 28 move solution is given by Benjamin L. Schwartz in
Journal of Recreational Mathematics 15:1 (1982-83) 31-38.
|
|
19
The Delbourgos' "How To Tackle the Tetrahedron" is available from them at
15 Willowdene Avenue, Sandy Bay, Hobart, 7005, Tasmania, Australia. Nicolas
Hammond has sent some of his computer results which he asserts solve all
those edge only processes which use at most 9 moves.
There is no method to just flip a pair of edges in less than 8 moves,
but Werneck and Meier give:
FR+RB+Uu = B'U'R'URBU.
The Groups of the Pyraminx. The constructible group (where we
allow just the edges to be removed) has 34·34·6!·26
= 3023 30880 patterns. The conservation rules are
that each move is an even permutation of edges and of edge faces. Hence
we can only get an even permutation of pieces and an even number of flips.
All such patterns are readily achieved, so the Pyraminx group has
34·34·6!·26 / 2·2 = 755 82720 patterns.
Since the corners and vertices can be moved independently of the edges,
the constructible group is the direct product (N59) Z34
× Z34 × (Z2 wr S6). The Pyraminx
group is the subgroup of index 4 (N39) obtained by restricting Z2
wr S6 to even permutations of position where the 'total flip' is
0 (mod 2).
God's Algorithm. The Pyraminx has 8 corner moves. After turning a
corner, we have 6 turns available at other corners. So the number of
patterns after n moves is at most Tn = 1 + 8 + 8·6 + 8·62
+ ... + 8·6n-1 = (8·6n - 3)/5. These are the patterns
where the vertices are not turned, so we are interested to know when
Tn exceeds 34·6!·26 / 2·2 = 933120. The
values of Tn are as follows.
| n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| Tn |
1 |
9 |
57 |
345 |
2073 |
12441 |
74649 |
447897 |
2687385 |
Hence God's algorithm must be at least 8 moves Long. Hammond's work
(C1-11) shows it is at most 13 moves long. (Add four moves if we consider
vertices as well.)
Pyraminx Patterns. Werneck's book gives a selection of patterns,
but most of these can be done in fewer moves. Ronald Turner-Smith "The
Amazing Pyraminx" gives more patterns than any other book. Though he does
not always give the best solution, he usually states what the least moves
known is. Some patterns have better solutions in the Pyramaths appendix.
20
We abbreviate sources as follows.
TDD - Tino & Daniel Delbourgo "How to Tackle the Tetrahedron"
NJH - Nicolas J Hammond
KM - Kersten Meier "The Small Magic Tetrahedron"
DP - David Peter
DBS - Myself
T-S - Ronald Turner-Smith "The Amazing Pyraminx"
WK - Well known
TW - Tom Werneck "Mastering the Magic pyramid"
| Jewel (T-S & TW) or Twist |
| Uu = (URUR')2 |
(T-S & WK - 8) |
| |
| Joseph's Coat (T-S) or Till's Windmill (TW) or 4-Jewels or 4-Twist |
| RrLlBbUu = (R'L')5 (U'B')5 |
(T-S - 20) |
| (T-S asserts 16 moves is possible.) Each half of this is a 2-twist. |
| |
| Queen's Jewel Box (T-S) or Fabian's Windmill (TW) or 4-twist |
| is the above followed by r'l'b'u' to give RLBU. |
| |
| Doors (T-S) or Holy Temple Gates (TW) or 3-V (TDD) |
| (FD, RD, LD) = RL'R'L'B'L'B |
(T-S & WK - 7) |
| |
| Cat's Paws (T-S) or Fire-Red Cat's Paw (TW) or Adjacent 2-flip |
| FR+FL+ = [R, U'] [R', L] |
(T-S & WK - 8) |
| |
| Gates at Gizeh (T-S) or 4-V (TDD) or Opposite 2-flip |
| LR+FD+ = L'U'LU'RUR'U |
(NJH & KM - 8) |
| This puts a door or V pattern on all four faces. There is another such
pattern mentioned without solution in T-S: |
| (FD, FL, RD) = R [U,L']R' |
(DBS - 6) |
| The square of this is another such pattern. |
| |
| 4-flip |
| FR+RL+LF+FD+ = L'U'LU'RBUB'UR' |
(NJH & KM - 10) |
| The configuration of edges FL, FD, RD, LR is a central square and its symmetries give interesting patterns. |
| |
| Sun and Moon (T-S) or Square 4-flip |
| FL+FD+RD+LR+ = BR'U'RU'BLUL'UB |
(KM & DBS - 11) |
| |
| King's Treasure Chest (T-S) or Tutankamen's Treasure Chest or 6-flip |
| FR+RL+LF+FD+RD+LD+ = (UR'L)3 |
(T-S - 9) |
| |
| Cleopatra's Needle (T-S & TW) |
| (FD, LD, RD) Uu = U'RU'R'LU'L'BU'B'RU'R' |
(T-S & TW - 13) |
| |
| Chariot (T-S) or Wagon Wheel (TW) or 3-wheeler |
| (FR, RL, LF)(FD, RD, LD) = RUR'URUL'R'L'B'L'B |
(DP - 12) |
| This rotates the edges 120° anticlockwise about the vertical axis. |
| |
| Chariots of Egypt (T-S) or 4-wheeler |
| FR+DL+(FL, RD)(FD, RL) = LBR'U'·BLU'R'·LBR'U' |
(DBS - 12) |
| This rotates the edges as a unit 180° about the midline
joining FR and DL. If one views the moves as moves of faces, rather than
corners, this is [R, L]3 which exchanges two pairs of corners! |
21
|
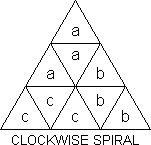
Priest's Pattern (T-S) or Whirlwind (TW). Let us call this face
pattern a clockwise spiral and its mirror image an anticlockwise spiral.
Four anticlockwise spiral faces correspond to a 6-flip and 4-clockwise-jewels:
| FR+ FL+ FD+ LR+ LD+
RD+ Uu Rr Ll Bb |
= LRBL'RL'R'L'UB'LBL' |
(DP - 13) |
TDD give a long pattern with 3 clockwise and one anticlockwise spiral
which I have simplified to:
| FR+RL+LF+(FD, DR, LD)+
U'u'R'r'B'b'L'l' |
= B'R'BL'B'U' |
(TDD & DBS - 6) |
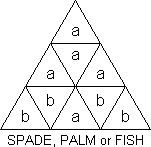
The face pattern shown is variously called spade (as in cards), palm
(tree) or fish.
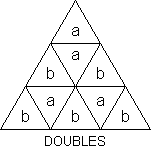
The next pattern is called Doubles (T-S). We can get 4-Doubles
in two ways.
| (FR, FD, LF, RL, DR) |
= ? |
(T-S asserts it can be done in 7) |
| |
| (FR, DL)(FL, DR) |
= [R, B][L, U][R, B] |
(DBS - 12) |
The latter is 180° rotation of the central square about the axis
LR-FD.
| 2-Doubles or 2 plain & 2 cat's eyes (T-S) |
| (FR, LR)(FD, LD) |
= R'BR'BRBR'BRBR'BR' |
(T-S & DBS - 13) |
This is a reflection of the central square in a bisecting plane through
the UL edge of the tetrahedron.
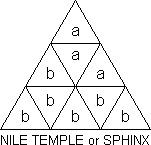
T-S calls this a (left) Nile Temple. I think it's clearly a (left) Sphinx.
He gives a method for 3 right Sphinxes and one left one. Can you get 4
rights?
|
|
22
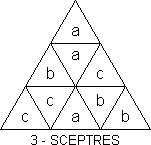 T-S calls this a 3-Sceptre face. He believes it is impossible to get four
3-Sceptres??
T-S calls this a 3-Sceptre face. He believes it is impossible to get four
3-Sceptres??
There are a number of other patterns in T-S and TW but they aren't as
interesting as the above.
CUBISM AND RELIGION (Cont. from C1-16)
Neil J. Rubenking writes from a Zen Center in California, and he sounds
like a serious Buddhist. He has produced a set of stickers which converts a
cube into a "Buddha's Cube". Each corner has a single noun three times and
each edge has a single verb twice. The resulting sentences across and down
express truths of various schools of Buddhism. The corner nouns are: Buddha,
delusion, emptiness, enlightenment, existence, Nirvana, the self, suffering.
The edge verbs are: abides in, conceals, contains, deceives, destroys,
hinders, is, is not, knows, liberates, produces, reveals. This gives a total
of 672 possible sentences and any configuration of the cube has 12 at a time.
Problem for the masochistic - is there a set of 56 cubes on which the 672
sentences occur once each. The centre stickers are "OM MANI PADME HUM",
which makes it a genuine Prayer Wheel. He has made a more complex version
for a Zen teacher with 24 words on the corner facelets and 24 words on the
edge facelets.
Corner triples:
| Buddha | ignorance | the self | concentration |
| Dharma | delusion | sentient beings | wisdom |
| Sangha | wrong views | existence | mindfulness |
| |
| joy | emptiness | enlightenment | Nirvana |
| equanimity | impermanence | liberation | no-self |
| compassion | suffering | the way | true suchness |
Edge pairs:
| is | conceals | destroys | liberates |
| is not | reveals | produces | hinders |
| |
| deceives | joins | abides in | saves |
| knows | parts from | contains | ignores |
| |
| penetrates | frees | sees | completes |
| obstructs | binds | surpasses | scatters |
Ian Williams sends an article from Aquarian Arrow by Lionel Snell
entitled "Notes towards the deployment of the Hungarian Magic Tube as a
system of divination".
"It is a portable permutable set ... smaller than the Rider Traveller's
Tarot." He allocates the following meanings to the three axes:
23
"Up, down = WILL (cf. the upright rod or phallic symbol of will)
Left, right = THINKING (cf. the "weighing up" motion of the balance)
Front, back = FEELING (cf. a reaching forward and a shrinking back towards yourself)"
He finds the cube more harmonious to Libran aesthetic sensibilities when
he recoloured his cube so
F = green, B = red, R = yellow, L = blue, U = white, D = brown (presumably
a dark orange?).
He finds planetary and other associations with the colours - e.g.
F = green, Venus, attraction ... !
PREHISTORY OF THE CUBE
As a result of the enormous publicity generated by the Cube, a number of
independent inventions of the idea have surfaced.
The first French book on the cube (Le Cube Hongrois by André
Deledicq and Jean-Baptiste Touchard) reports: "In fact, Inspector General
Semah says he played with a similar cube (but in wood) in 1920 in Istanbul,
then about 1935 in Marseilles (with a cube of five white faces and one green
face)." Touchard says he went to see Semah, who is now an old man, but who
seemed to recognise the cube as an old friend. In view of the Middle Eastern
tradition of puzzle rings and the Far Eastern tradition of puzzle boxes and
other wooden puzzles, I think there is some probability that a wooden cube
might have been made by some craftsman, The cost of wooden cubes would have
been prohibitive and only a few (one?) would have been made. I would be
delighted if anyone can find more evidence of such a cube.
In 1960, a mathematics teacher named Gustafson, in Fresno, California,
invented the 23 Magic Sphere, but only conceptually at first.
One of his students, Dick Walton, reports that his class discussed the
mathematics and possible mechanisms at length. Gustafson eventually proposed
having a central sphere with grooves. I have been told that Gustafson
obtained a patent on this, but I have not yet tracked it down.
Larry D. Nichols, of Arlington, Massachusetts, filed for a US patent
for "Pattern forming puzzle and method with pieces rotatable in groups"
on 4 March 1970. This was granted as Patent no. 3,655,201 on 11 April 1972.
This is for a 23 with a magnetic mechanism The concept of a magic
cube is clear. However the magnetic mechanism works by separating the cube
in half, then turning and putting the halves back together. If you try to
rotate a half, magnetic repulsion pushes the halves apart. This is achieved
by putting three small bar magnets on the inner faces of each cubelet as
shown. So the mechanism is not at all like Rubik's. In particular, one can
cheat too easily by disassembling the cube.
24
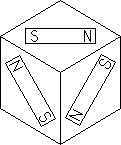 However, Nichols refers to other shapes and sizes, and "engagement
by mechanical rather than magnetic means, as for example by using a pop-in
snap linkage, or a tongue-in-groove arrangement".
Nichols' company, which holds the patent rights, has written to Ideal
claiming prior invention. Ideal feels that the cube does not infringe
Nichols' patent. Nichols company has recently filed suit for $60,000,000!
However, Nichols refers to other shapes and sizes, and "engagement
by mechanical rather than magnetic means, as for example by using a pop-in
snap linkage, or a tongue-in-groove arrangement".
Nichols' company, which holds the patent rights, has written to Ideal
claiming prior invention. Ideal feels that the cube does not infringe
Nichols' patent. Nichols company has recently filed suit for $60,000,000!
The New York Times reports that Nichols' firm, Moleculon Research Corp.,
did try to market Nichols' idea in 1969 but wouldn't divulge the secrets
until the patent came through. It was rejected by all the firms approached,
including Ideal, generally because of the secrecy.
I hesitate to predict the outcome. Though Nichols has the concept, his
claim (quoted above) must be stretched rather far to cover Rubik's mechanism
and Gustafson's patent would seem to pre-empt Nichols. However, a large US
law firm has taken the Nichols case on a contingency fee basis - i.e. they
only get paid if they win! Gustafson has apparently stated that a cubical
version did not occur to him.
Frank Fox of Bletchley, Bucks, filed for a UK patent on an "Amusement
Device" on 9 April 1970 and this was published as UK patent 1,344,259 on
l6 January 1974. This was for a 33 in spherical shape, using
tongue and groove linking to hold the 26 exterior pieces together, leaving
the centre hollow. Fox thought to use this as a kind of board for noughts
and crosses (= tic tac toe), though he mentions use of 26 colours and the
use of letters and numbers.
LOCAL MAXIMA
Consider the Cayley graph of the Cube group. We say a position P is a
local maximum if it is further away from I than any of its 12 neighbours
- i.e. PR, PR', PL, PL',... The 12-flip is a local maximum. Let P be
any process which produces the 12-flip. Consider the last move of this
process, say it is R. Since the pattern is symmetric with respect to the
rigid motions of the cube and a mirror image of the process will give the
same effect, we can transform P into processes which end with R', L, L', ...
Any neighbour of P is thus obtained from some transform of P with the last
move omitted, hence is obtained in one move less than P itself. There is
no other pattern which is symmetric under all the rigid motions of the
cube, but there may be a pattern with less symmetry which can be obtained
by several processes of the same length such that we can obtain the pattern
with any move at the end. Such a pattern will also be a local maximum.
25
THE TRIALS OF THE CUBE
Ideal Toys and Politoys (the new name of Politechnika commenced legal
action against the Taiwanese 'knock off' cubes early in 1981. The first
case to reach court was against Dallas Print Transfers and Dallas Marketing,
two London distribution firms run by Alec Yuen. After many postponements,
this case began on 25 January and lasted twelve days! There were two grounds
- infringement of copyright and 'passing off'. UK copyright law is nearly
unique in extending to working or production drawings. Copying of a three
dimensional object made from the drawings infringes on the copyright in
them. 'Passing off' means selling an imitation product which is so similar
to an established original as to mislead the public. The defendants first
claimed that the drawings produced were not the basis of the copied cube.
This was due to the fact that Politoys first sent the drawings for the
pre-1980 cube rather than those for the later production which was the
basis for the copied cubes. Once the correct drawings were produced and
the draughtsman, Miss H. Czák, made it clear that she had made both
sets of drawings, then the infringement of copyright was established and
the judgment upheld this. I thought 'passing off' was also clear, but Ideal
was held not to have established that they had created a brand image, due
to the pre-1980 sales and the lack of image promotion. Damages have not yet
been assessed and Dallas is appealing the judgment. However, I have recently
heard that the whole Dallas operation has gone bankrupt.
Cases have taken place in Holland and the US. In Holland the case went
through several hearings and I am unclear as to the final outcome. In the
US, Ideal has obtained several injunctions and is attempting to block the
importation of pirate cubes.
I have heard from a student doing a law thesis on the cube. She has
offered to write a summary for the Circular.
A CZECH CHECK PROBLEM
The Czech weekly, Mladý Svet (Young World), poses as an exercise
the problem of having each face with 8 facelets of one colour. The other
facelet is a second colour but can be at the centre or an edge or a corner.
If all are at the centre, we have 6-spot; if all are at edges, we can get
it easily as (UL, FD, RD); if all are at corners, we can get it easily as
URF+BLD-. However, there may be other ways of getting
these effects and one might have different places for the odd coloured
facelets - or can one?
26
GOD'S ALGORITHMS
In C2-8, I discussed an improved lower bound for God's algorithm. I have
since realised that the argument can be refined a bit. Recall that
Sn is the number of sequences of n 90° moves with the obvious
redundancies excluded. Previously I totaled Tn = S0
+ S1 + ... + Sn until Tn > N. But each
90° move is an odd permutation of the corners and of the edges, so
U2m = U2m+1 = S0 + S2 + ... +
S2m is the number of sequences which give even permutations on
corners and on edges while V2m+1 = V2m+2 =
S1 + S3 + ... + S2m+1 is the number of
sequences giving odd permutations on corners and edges. Both these sums must
be >= N/2 = 2.16 × 1019. It turns out that
S20 = 3.56 × 1019, T20 = 3.98 × 1019, U20 = 3.60 × 1019,
S21 = 3.33 × 1020, T21 = 3.73 × 1020, V21 = 3.37 × 1020,
so that the refinement gives no gain, although I thought at first it
would.
However, if we consider the supergroup, we want Tn,
Un and Vn >= 2048·N/2 = 4.43 ×
1022. Here T24 = 3.07 × 1023,
U24 = 2.78 × 1023, V24 = 2.96 ×
1022, so we do need to go one step further to get
U25 = 2.60 × 1024 and God's algorithm for the
supergroup has length > 25, instead of 24.
Herb Taylor has passed on some further results.
The 23 square group was observed to have 24 patterns, diameter
4 and 5 antipodes at N53/54. Taylor points out that the Cayley graph can be
drawn on a torus with 12 hexagonal faces. The number Nd of
positions at distance d from a position is given by
According to Joe Buhler, via Herb Taylor, three different programs have
found the diameter of the 23 is 11. One of these was circulated
as a UNIX news item. It took over 51 hours of computer time. Don Knuth, the
well-known Stanford computer scientist, gave the problem to a graduate class,
but wanted R2 to be counted as two turns, etc. Buhler recollects
that this gives diameter 14 and says that this was done by Joan Feigenbaum
or Richard Anderson. (Several people have suggested that we write 14q when
we mean quarter or 90° turns. This seems useful.) The UNIX news item
gives the following table for Nd.
27
| d | Nd |
| 1 | 9 |
| 2 | 54 |
| 3 | 321 |
| 4 | 1847 |
| 5 | 9992 |
| 6 | 50136 |
| 7 | 2 27536 |
| 8 | 8 70072 |
| 9 | 18 87748 |
| 10 | 6 23800 |
| 11 | 2644 |
Using simple counting, as at N26 and 60, one sees that some positions
require at least 9 moves. There are no obvious redundancies to account for
(we are keeping one corner fixed), so I expected a diameter less than 15.
An antipode of START is
FRFRF D2FD'FD2R2 = (UFL, RBD, LDB, UBR,
FUR, DLF, FRD)
One of the groups who did the 23 went on to the 33
square group. They get diameter 15 which confirms Thistlethwaite's conjecture
(N39) and hence reduces his algorithm to at most 50 moves. The numbers
Nd are as follows
| d | Nd |
| 1 | 6 |
| 2 | 27 |
| 3 | 120 |
| 4 | 519 |
| 5 | 1932 |
| 6 | 6484 |
| 7 | 20310 |
| 8 | 55034 |
| 9 | 1 13892 |
| 10 | 1 78495 |
| 11 | 1 79196 |
| 12 | 89728 |
| 13 | 16176 |
| 14 | 1488 |
| 15 | 144 |
The fact that these diameters are small leads me to believe that the
length of God's algorithm will be about 22. However, it seems unlikely that
there will be a unique antipode. The UNIX news item concludes "I just thought
of a lovely way to get the answer for the 3 ×3 × 3 cube, but the margins on
this news item are a little bit too small for me to include it."
The UNIX news item is a rather faint copy, but further examination shows
that it comes from duke!chico!esquire!
Frank O'Hara has found the diameter of the antislice group is 8 antislice
moves. (N54)
© David Singmaster
28

The text and original drawings are copyright © David Singmaster, reproduced here with
permission. Conversion to html and additional commentary by Jaap Scherphuis.
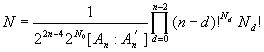
 An article in La Recherche last December is partly by Raoul Raba inventor
of the Rotascope (
An article in La Recherche last December is partly by Raoul Raba inventor
of the Rotascope (

 Over the years there have been a number of 'fiddlies' based on hinging
together 8 cubes along edges so that they will fold into a 23.
The best known of these has its 8 cubes joined in a ring as shown in the
diagram. The cubes are shown from above. Some of the vertical faces where
cubes meet have hinges joining their edges as indicated by the letters. When
the front and back pairs of cubes are folded up, we have a 23.
The folding can be continued through three more steps to give another
23. But then all the cubes are inverted so their previous
outsides are inside and vice versa This fiddly has been known long enough
that origamists can make the whole thing from a single strip of paper.
(There are also a number of other hingings. If the R and L are changed to L
and R and the back D is changed to B and the front D is changed to F, the
result can be folded into a cube in four ways with a tricky move required
to get between two sets of two ways.)
Over the years there have been a number of 'fiddlies' based on hinging
together 8 cubes along edges so that they will fold into a 23.
The best known of these has its 8 cubes joined in a ring as shown in the
diagram. The cubes are shown from above. Some of the vertical faces where
cubes meet have hinges joining their edges as indicated by the letters. When
the front and back pairs of cubes are folded up, we have a 23.
The folding can be continued through three more steps to give another
23. But then all the cubes are inverted so their previous
outsides are inside and vice versa This fiddly has been known long enough
that origamists can make the whole thing from a single strip of paper.
(There are also a number of other hingings. If the R and L are changed to L
and R and the back D is changed to B and the front D is changed to F, the
result can be folded into a cube in four ways with a tricky move required
to get between two sets of two ways.) The halving used by Yoshimoto is also given by Slothouber. Consider the
cube divided into 6 square pyramids, based on the faces with the apices at
the cube centre. Three of these meeting at a corner are a half-cube congruent
to the other half. The interior form is a star-like solid which rejoices in
the name of the stellated rhombic dodecahedron. Each point of the star is a
rhombic pyramid on a face of the rhombic dodecahedron. The shape is fairly
well known because a popular assembly puzzle forms this shape from 6 pieces.
(There are two versions - one with different pieces, including a key piece
and the other with 6 identical pieces which is more interesting.)
The halving used by Yoshimoto is also given by Slothouber. Consider the
cube divided into 6 square pyramids, based on the faces with the apices at
the cube centre. Three of these meeting at a corner are a half-cube congruent
to the other half. The interior form is a star-like solid which rejoices in
the name of the stellated rhombic dodecahedron. Each point of the star is a
rhombic pyramid on a face of the rhombic dodecahedron. The shape is fairly
well known because a popular assembly puzzle forms this shape from 6 pieces.
(There are two versions - one with different pieces, including a key piece
and the other with 6 identical pieces which is more interesting.)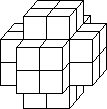
 About two years ago, Diane Turnbull brought me an example of a 'folding
cube'. It consists of 27 cubes strung together with elastic. The cubes have
holes which go from a face centre to a face centre, either directly opposite
a straight piece) or adjacent (a bend piece) as shown. The object is to fold
it into a cube. For a particular arrangement of straight and bend pieces it
takes about half an hour to check all possibilities. The example brought to
me has only one solution as a 33 and no solution as a 3 × 9
rectangle. It struck me that it might be possible to have all bend pieces.
However, I have shown that one must have at least two and at most eleven
straights among the 25 interior pieces. (The end pieces cannot be classified
as straight or bend since the string doesn't continue.)
About two years ago, Diane Turnbull brought me an example of a 'folding
cube'. It consists of 27 cubes strung together with elastic. The cubes have
holes which go from a face centre to a face centre, either directly opposite
a straight piece) or adjacent (a bend piece) as shown. The object is to fold
it into a cube. For a particular arrangement of straight and bend pieces it
takes about half an hour to check all possibilities. The example brought to
me has only one solution as a 33 and no solution as a 3 × 9
rectangle. It struck me that it might be possible to have all bend pieces.
However, I have shown that one must have at least two and at most eleven
straights among the 25 interior pieces. (The end pieces cannot be classified
as straight or bend since the string doesn't continue.)






 T-S calls this a 3-Sceptre face. He believes it is impossible to get four
3-Sceptres??
T-S calls this a 3-Sceptre face. He believes it is impossible to get four
3-Sceptres?? However, Nichols refers to other shapes and sizes, and "engagement
by mechanical rather than magnetic means, as for example by using a pop-in
snap linkage, or a tongue-in-groove arrangement".
Nichols' company, which holds the patent rights, has written to Ideal
claiming prior invention. Ideal feels that the cube does not infringe
Nichols' patent. Nichols company has recently filed suit for $60,000,000!
However, Nichols refers to other shapes and sizes, and "engagement
by mechanical rather than magnetic means, as for example by using a pop-in
snap linkage, or a tongue-in-groove arrangement".
Nichols' company, which holds the patent rights, has written to Ideal
claiming prior invention. Ideal feels that the cube does not infringe
Nichols' patent. Nichols company has recently filed suit for $60,000,000!